直板清管器与管壁间摩擦阻力的模拟研究
曹学文 曹恒广 赵湘阳 杜 翰 李星標 杨亚吉
(中国石油大学(华东)储运与建筑工程学院)
0 引 言
伴随着天然气资源的进一步开发,输气管道在石油天然气工业中的作用也越来越大[1-2]。然而输气管道在长期运行后,管内会出现游离水、凝析油和黑粉等降低管道输气能力的情况,因此天然气输送管道需要定期进行清管作业[3-9]。清管器作为管道清理的主要工具,在输气管道清理中的应用不可或缺。常规清管器包括清管球、泡沫清管器和直板清管器等[10-16]。清管器一般依靠密封盘与管道内壁形成密封,在管输流体的推动下沿着管线向前移动,刮除管壁污垢,将堆积在管道内的杂质推出管外,从而达到清洁管道的效果[17]。密封盘的力学行为直接影响清管器的通过性及清洁能力,其中清管球清理固体杂质能力较差,泡沫清管器耐磨性差不能重复使用,在清理积液时直板清管器往往具有更好的效果。目前,由直型橡胶皮碗、隔离盘和导向盘等组成的刚体式直板型清管器能够双向运行、杂物清理能力强且技术成熟,因此应用较为广泛[18-19]。
为了预测清管器在管道内部的运行状态,通常需要建立清管动力学模型。作为清管过程中受到的主要作用力,摩擦阻力是决定清管器动力学特性的关键因素,它直接影响清管器的运行状态。清管过程中,清管器所受的摩擦阻力是多种因素综合作用的结果[20-22]。因此,确定清管过程中直板清管器摩擦特性的变化规律是建立清管动力学模型的基础。前人利用有限元分析软件对清管器的变形过程建立了有限元模型[23-26],研究了直板皮碗和碟形皮碗的接触性能,得出皮碗过盈量、厚度与皮碗接触应力的关系,求解了清管器运行所需的压力。但是关于皮碗与管壁之间摩擦力的量化以及皮碗夹持率对摩擦力的影响却鲜有研究。鉴于此,笔者以直板型皮碗清管器清理天然气管道为背景,利用有限元软件ANSYS建立数值模型,分析了过盈量、直板厚度和夹持率等因素对清管器摩擦阻力的影响,研究了直板清管器运动过程中摩擦力的变化规律,以期为直板清管器密封皮碗的选择、清管器运行速度以及清管时间的估算提供理论依据。
1 摩擦力的理论计算
直板清管器结构如图1所示,其主要由2片导向盘、4片密封盘(直板皮碗)、隔离盘及钢骨架等组成。密封盘直径大于管内径,导向盘直径略小于管内径,即摩擦主要由密封盘过盈产生,因此在分析清管器与管壁间摩擦时可以先分析单片密封盘的受力情况,进而考虑全部密封盘的受力情况,从而得到清管器的整体受力分析结果。
清管器在发球筒内起始处于静止状态,其所受摩擦为静摩擦,静摩擦力Ff大小等于清管器前后压差;当管道入口流量增大,清管器即将运动的临界时刻,所受静摩擦力为最大静摩擦力,数值约等于动摩擦力Fc;当其前后压差足以克服清管器与管道内壁之间摩擦阻力后便开始运动,其所受摩擦为动摩擦。

1—导向盘;2—密封盘(直板皮碗);3—隔离盘;4—钢骨架。图1 直板清管器结构图Fig.1 Structure of straight plate pig
由于天然气管道以及清管器隔离盘的刚度远高于直板皮碗的刚度,所以清管器进入管道后其密封直板会发生变形[27],同时可将管壁和隔离盘视为刚性构件。清管器密封盘结构与受力如图2所示。
清管器密封盘受力沿径向均匀分布,可从二维轴对称方向对单个密封盘受力进行分析。研究表明,清管器重力引起的总接触力为0,即清管器重力引起的总摩擦力为0,故在受力分析过程中忽略了重力对清管器的影响[28]。根据O’Donoghue皮碗圆弧变形的假设建立了皮碗变形的简化模型,在建模及求解过程中,忽略清管器密封盘上可能存在的倒角,即实际所受摩擦力为沿密封盘边缘发生的磨损所致[29-30]。

图2 清管器密封盘结构与受力示意图Fig.2 Structure and stress of pig seal disc
如图2所示,假设密封盘的中心线可以用半径为R、圆心角为α的圆弧表示,不考虑径向压缩时,中线的长度l可被认为是常数,则密封盘中线径向投影长度l′的计算式为:
(1)
式中:l′为密封盘中线径向投影长度,m;rd为密封盘半径,m;rp为管道内半径,m;rf为隔离盘的半径,m;δ为密封盘厚度,m;α为密封盘弯曲角度,(°)。
直板清管器密封盘与管壁的接触长度Δx以及接触面积S的计算式分别为:
(2)
S=2πrpΔx
(3)
沿清管器径向截面取圆心角为dθ的微元体,微元体上由摩擦力Ffric在A点产生的力矩Mfric计算式为:
Mfric=Ffric(rp-rf)rpdθ
(4)
式中:Mfric为摩擦力力矩,N·m;Ffric为密封盘单位长度所受摩擦力,N/m。
对于天然气管道,结合库伦摩擦定律可推导出A点所受管壁正压力的力矩为:
(5)
式中:μdry为天然气管道摩擦因数;Mwall为管壁正压力力矩,N·m。
由压缩弯曲应力σc和拉伸弯曲应力σt引起的A点的力矩计算式为:
(6)
式中:E为密封盘弹性模量,Pa;Mc为压缩弯曲应力力矩,N·m;Mt为拉伸弯曲应力力矩,N·m;I为密封盘围绕点A的惯性矩,可按式(7)计算。
(7)
直板型密封盘在周向被压缩,由环向应力引起的A点的力矩为[24]:
(8)
式中:μ为泊松比,无量纲。
假设清管器在天然气管道内运动为稳态运动,考虑图2中A点的力矩平衡,所以内力力矩和外力力矩之和应等于0,则A点总力矩平衡式为:
∑M=(Mfric+Mwall)-(Mc+Mt+Mθ)=0
(9)
密封盘在微元角dθ上所受的摩擦力Ffric为方程的唯一未知量,将式(4)~式(6)、式(8)代入式(9)得:
(10)
(11)
以内径317.4 mm的天然气管道为例,管道采用聚氨酯直板皮碗清管器进行清管。清管器密封盘的直径334 mm,厚度为14 mm,弹性模量为20 MPa,泊松比为0.5;清管器隔离盘的直径为200 mm。
将rd=167 mm、rp=158.7 mm、rf=100 mm、μdry=0.55、μ=0.5、δ=14 mm带入式(1)和式(11)得:
(12)
(13)
(14)
最终利用MATLAB软件可求得α=1.193 3 rad=68.37°,R=0.056 15 m,Fc=4 272.7 N,因此天然气管道内单个聚氨酯密封板所受摩擦力为4.27 kN,则该直板皮碗清管器在水平管段的摩擦阻力f=nFc=4×4.27 kN=17.08 kN。
2 有限元模型数值分析
根据清管器直板的受力分析结果,采用ANSYS动力学分析软件建立了对应的有限元模型,对清管器直板在天然气管道中的变形进行模拟计算,获得清管器与管壁间的摩擦阻力。与密封盘和管道之间的接触力相比,清管器的重力通常可以忽略不计[28]。建立的几何模型如图3所示。因为管道以及清管器的对称性,聚氨酯直板清管过程受力的有限元模型几乎是对称的,为了节省计算资源,可以建立清管器截面受力模型,利用ANSYS内部的接触模块进行求解。模拟过程中清管器进入管道的过程缓慢,最后的平衡状态就是清管器的聚氨酯直板在管内的变形情况。

图3 清管器聚氨酯直板变形的几何模型Fig.3 Geometric model for simulating deformation of polyurethane straight plate of the pig
PLANE 182单元由4个节点定义,可用于平面单元或轴对称单元,具有塑性大变形以及大应变等功能,因此通过PLANE 182单元对模型进行划分网格。建立聚氨酯直板与钢骨架和管壁的摩擦接触,对管道外壁添加X和Y方向的约束,限制密封盘Y方向的自由度。为了便于收敛,管道入口处的直角被圆角代替,建立的清管器直板有限元模型如图4所示。模拟使用的密封盘参数与试验用管道的参数相同,模拟中管道外径为355.6 mm,厚度为19.1 mm,密封盘直径为334.0 mm。
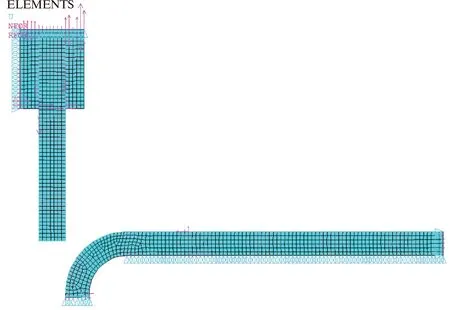
图4 清管器直板有限元模型Fig.4 Finite element model of straight plate of pig
清管器直板采用聚氨酯材料,其最显著的特点就是在很小的力的作用下就可以产生较大的变形,即橡胶的超弹性,该特点使得聚氨酯橡胶广泛应用于密封元件领域[31]。
描述橡胶材料的本构模型主要有Gent模型、Yeoh模型和Mooney-Rivlin模型等[32]。Gent模型和Yeoh模型拟合橡胶材料大变形时的应变能结果比较好,而Mooney-Rivlin模型可以较好地拟合橡胶材料中等变形时的应变能。因此本文采用模拟直板中等变形的Mooney-Rivlin模型,其应变能函数表达式为:
(15)
式中:I1、I2、I3为变形张量不变量。
变形张量不变量的表达式为:
(16)
式中:λ1、λ2、λ3为主伸长比。
假设密封盘具有线弹性,其拉伸模量与压缩模量相同。对于不可压缩材料,I3=1,则方程(16)简化为:
(17)
方程(17)前两项为:
W=C10(I1-3)+C01(I2-3)
(18)
式中:C10、C01为Mooney-Rivlin模型材料参数。
根据泊松比μ=0.5,可得聚氨酯橡胶Mooney-Rivlin模型常数C10=0.949,C01=0.475。
采用上述参数进行模拟,得到清管器直板在管道内的变形情况,如图5所示。

图5 清管器直板变形前后对比图Fig.5 Straight plate of pig before and after deformation
变形后直板上的应力分布情况如图6所示。由于隔离盘对聚氨酯直板的约束,在隔离盘约束的端部会产生一个应力集中,所以隔离盘端部也需要进行防护。在模拟中得到了清管器直板与管道在径向上的接触力,根据接触面积计算出清管器直板与管壁的摩擦力。清管器与管壁结构参数相同,将清管器与天然气管道内壁间摩擦力的计算结果同数值模拟结果进行对比分析,分析结果表明,数值模拟结果与理论计算结果的相对误差为4.92%,该值在误差允许范围内。
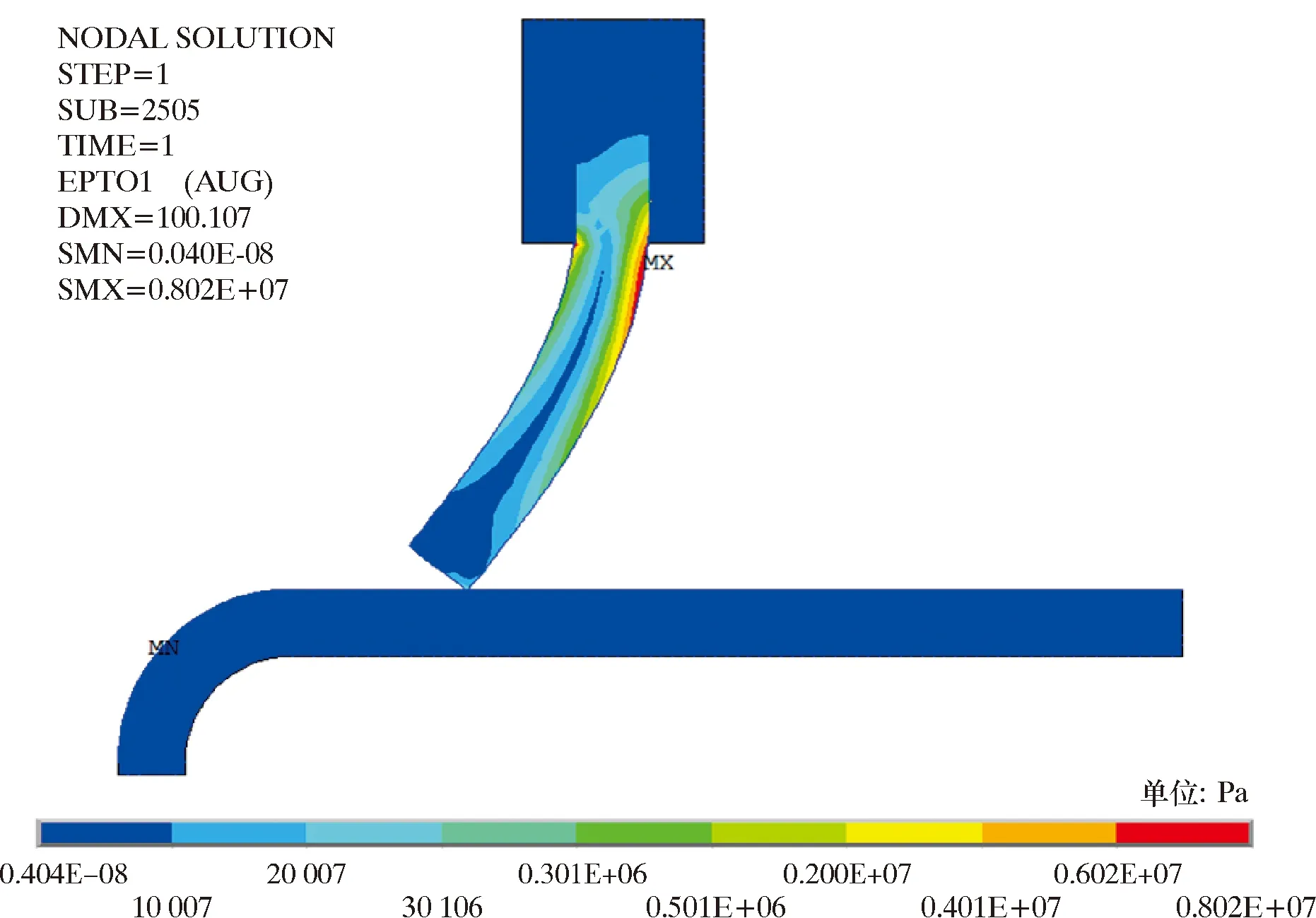
图6 清管器直板变形后应力分布的有限元模拟结果Fig.6 Finite element modelling result of stress distribution after straight plate deformation of pig
3 清管器牵拉试验结果对比
为进一步验证有限元分析结果的准确性和实用性,对直板清管器通过水平光滑管道的摩擦力进行了牵拉试验。试验用直板清管器和试验管道分别如图7和图8所示。

图7 现场试验用直板清管器Fig.7 Straight plate pig used in field test

图8 清管器摩擦阻力试验管道Fig.8 Pipeline for testing frictional resistance of the pig
试验管道外径为355.6 mm,壁厚为19.1 mm,内径为317.4 mm;直板清管器的密封盘过盈量为5.23%,导向盘直径为316.0 mm,密封盘厚度14.0 mm。现场通过牵拉装置作为动力进行匀速牵拉,将清管器从25 m的试验管段一端牵拉至另一端出口,牵拉速度为0.2 m/s。采用数字测力计测试实际牵引力的大小。
当直板清管器在试验管道中匀速运动时,数字测力计显示拉力为18.00 kN。数值模拟的结果为16.24 kN,模拟结果与试验结果的相对误差为9.78 %。因此,建立的有限元模型具有适用性,可用于计算清管器与管壁之间的作用力。试验测量的摩擦阻力数值比理论计算的结果偏大,这是由于试验管道已经出现一定程度的腐蚀,导致管壁与聚氨酯密封盘之间的摩擦因数增大,并且理论计算中忽略了清管器重力的影响。
4 不同结构参数对摩擦力的影响
清管器的结构尺寸参数直接影响直板与管道之间的接触状态,因此清管器和管壁之间的作用力与直板过盈量、直板厚度、隔离盘的直径有关。下文将针对内径为317.4 mm的天然气管道,采用ANSYS软件探究不同直板过盈量、直板厚度、隔离盘直径对清管器与管壁之间的摩擦力的影响。在实际应用中,常用夹持率ζ、过盈量ε以及厚度δ定义清管器的直板密封盘的尺寸特征。定义公式如下:
(19)
(20)
4.1 直板过盈量对摩擦力的影响
在直板夹持率相同(40%)和厚度相同(14 mm)情况下,研究过盈量对直板与管壁摩擦力的影响,结果如图9所示。
由图9可知,当夹持率、直板厚度相同而过盈量不同时,不同过盈量的直板与管壁接触产生不同程度的弯曲,直板的弯曲角度随着过盈量的增加而增大。这是由于当管道内径一定时,密封盘必须产生一定的弯曲角度才能在管道内运行,而过盈量越大,需要的弯曲角度越大。
当清管器在管道内运行时,密封盘与管壁的实际接触面积较小,密封盘外端面边缘与管壁形成线面接触,直板的接触应力最大值出现在直板与管壁的接触处。密封直板过盈量对摩擦力的影响如图10所示。
由图10可知,清管器密封直板过盈量越大,直板与管壁之间的作用力越大,呈对数上升趋势,上升速度逐渐减缓。这与李苗[27]和A.NIECKELE等[33]的研究结果一致。对图10中的曲线进行拟合,得到摩擦力与过盈量的关系式:
Fc=1 890.2+1 367.5ln(ε-0.278 4)
(21)
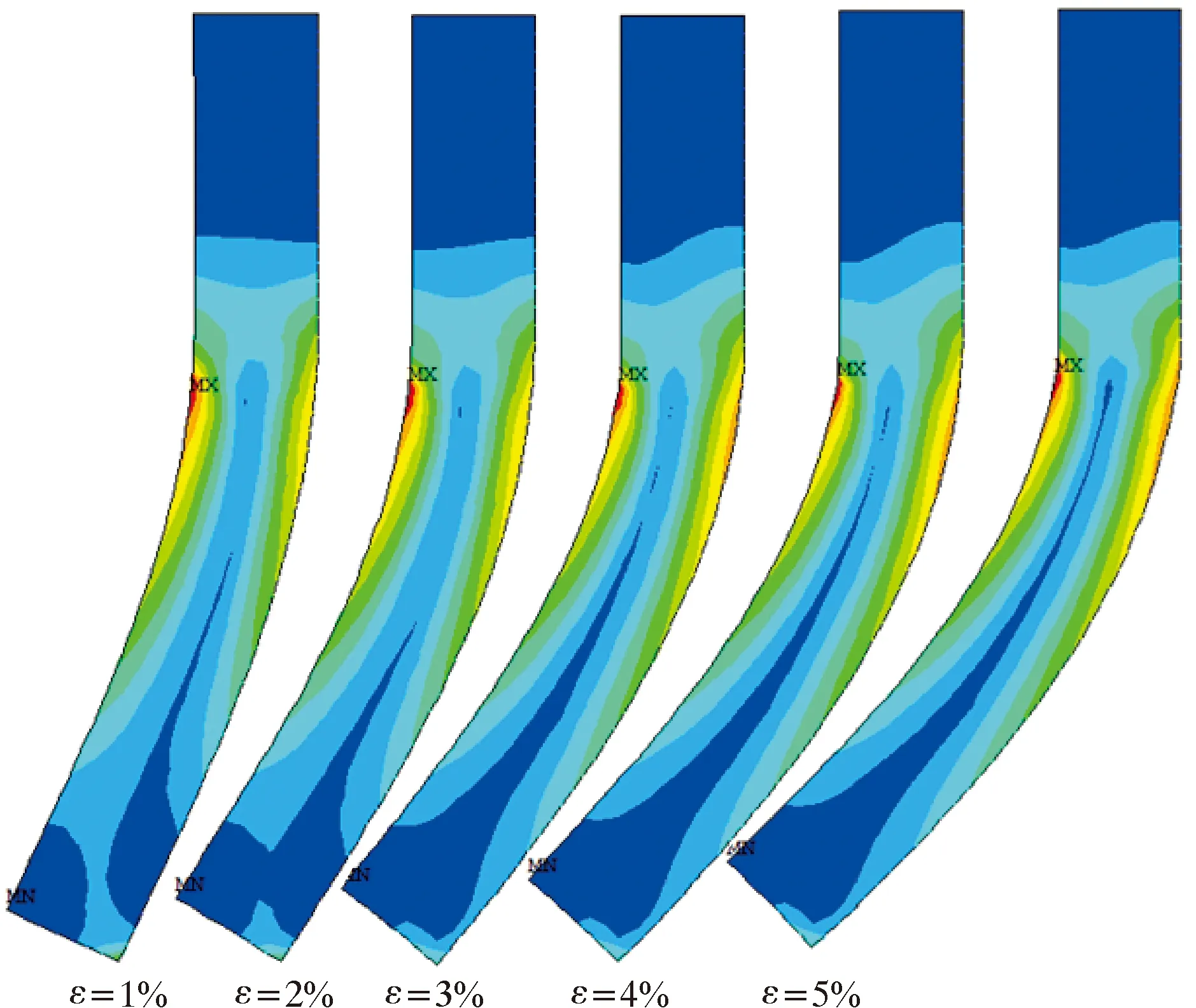
图9 不同过盈量直板应力分布云图Fig.9 Stress distribution cloud chart of straight plate with different interferences
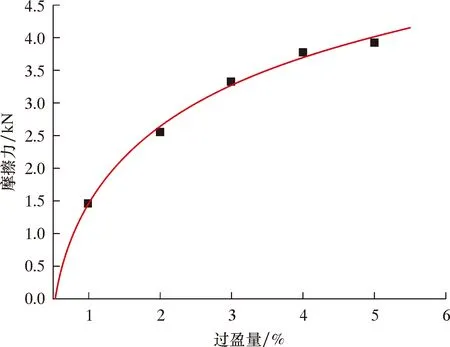
图10 密封直板过盈量对摩擦力的影响Fig.10 Effect of sealing straight plate interference on friction force
清管器过盈量一般为管径的3%~5%,在此过盈量下直板清管器一个密封直板与清管器之间的摩擦力范围为3 259~4 013 N。过盈量较小时,密封盘与管壁主要是线面接触,直板径向受压,与管道的接触面积虽然小,但是承受接触压力较大,随着过盈量逐渐增大导致摩擦力增加幅度较大;当过盈量较大时,直板产生了较大的弯曲,与管壁逐渐形成面面接触,接触面积增大,接触压力减小,摩擦力增加幅度反而变小。过盈量超过一定程度时,清管器将很难进入管道内。同时,过盈量越大,清管器以及管壁承受的磨损也较大,可能导致存在内涂层管道的内涂层被破坏。因此需要充分考虑清管效率以及清管器磨损的前提下,选择合适的过盈量。
4.2 直板厚度对摩擦力的影响
在直板夹持率相同(40%)和过盈量相同(3%)情况下,研究直板厚度对直板与管壁间摩擦力的影响,结果如图11和图12所示。由图11可知,在直板夹持率和过盈量相同而厚度不同时,密封直板的弯曲角度随着直板厚度的增加有缓慢增大趋势,但是变化较小。分析认为,管道的内径是一个定值,相同过盈量的密封直板需要弯曲同样的角度才能在管道内运行。随着厚度增加,直板内部受力面积比例增大,且直板与管壁接触面积和受力面积明显增大。
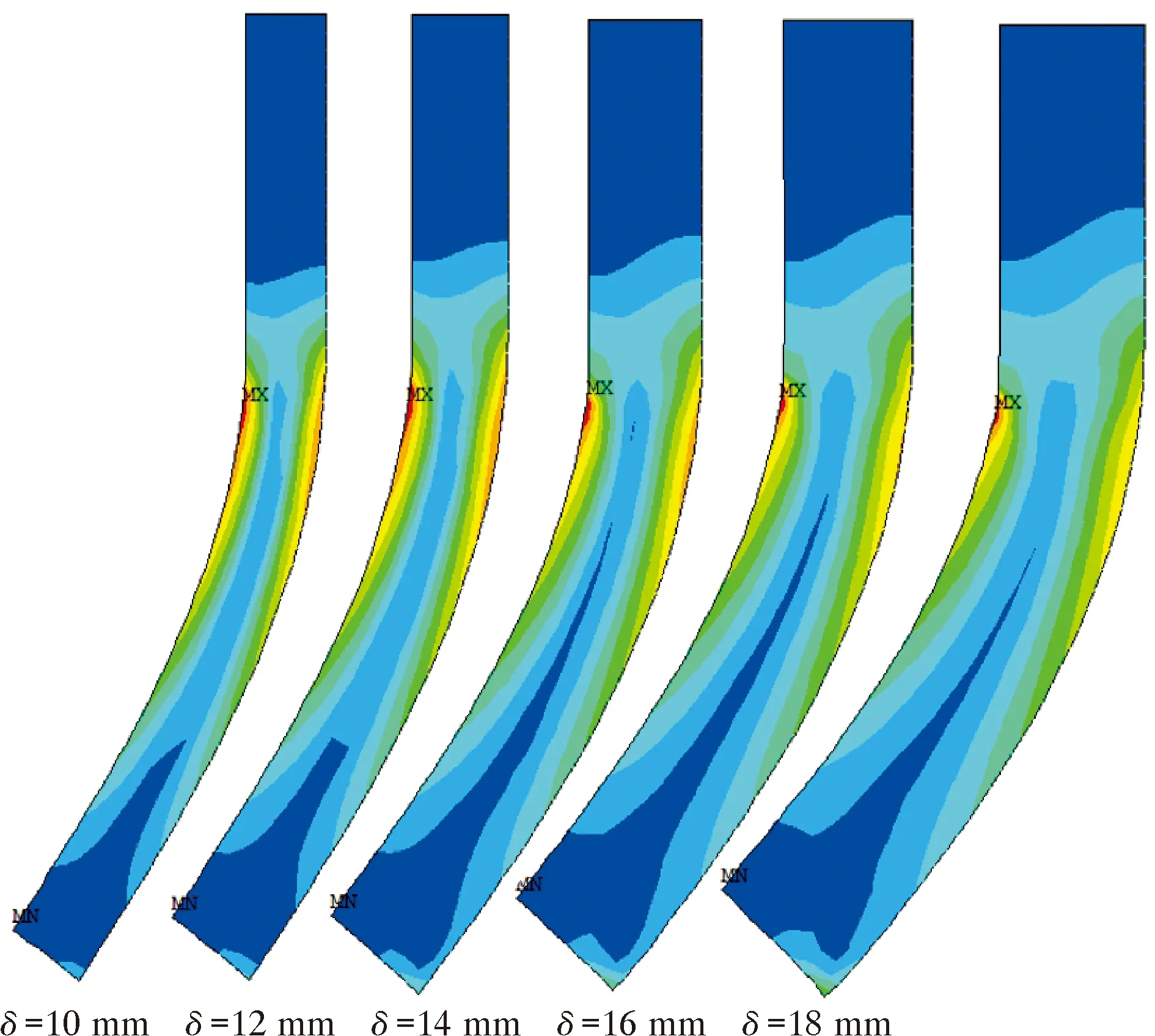
图11 不同厚度直板应力分布云图Fig.11 Stress distribution cloud chart of straight plate with different thicknesses

图12 不同直板厚度对摩擦力的影响Fig.12 Effect of different straight plate thicknesses on friction force
由图12可知,在夹持率和过盈量相同时,清管器与管壁之间的摩擦力随着直板厚度的增加而增大,且直板厚度越大,增加幅度越大。直板厚度的增加提高了直板弯曲的难度,随着直板厚度的增加,弯曲应力会增大,导致接触压力和接触面积增大,从而使得摩擦力明显增大。
4.3 夹持率对摩擦力的影响
在直板过盈量相同(3%)和直板厚度相同(14 mm)情况下,对36%、39%、42%、45%和48%这5种夹持率进行数值模拟分析,研究夹持率对直板与管壁摩擦力的影响。清管器的隔离盘对密封直板起到夹紧作用,限制了密封直板的变形,隔离盘直径越大,密封直板越难变形。不同夹持率下直板应力分布云图如图13所示。由图13可知,直板厚度和过盈量相同而夹持率不同时,随着夹持率增大,密封盘弯曲角度明显增大,且内部应力分布明显增大,管壁接触面积和接触压力增加。因为夹持率越大,在相同过盈量下的密封盘需要弯曲更大的角度才能在管道内运行。
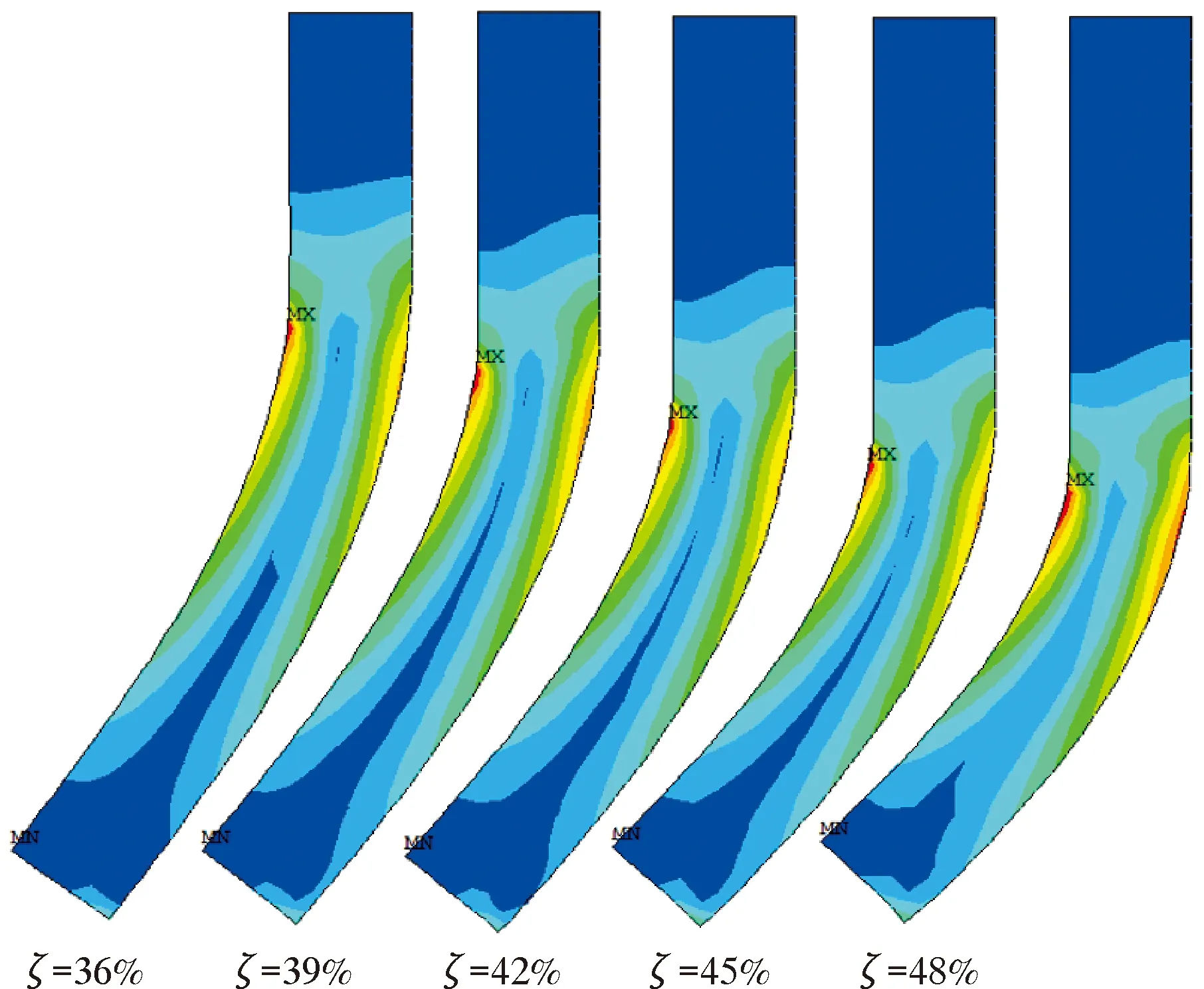
图13 不同夹持率直板应力分布云图Fig.13 Stress distribution cloud chart of straight plate with different gripping rates
不同夹持率直板对摩擦力的影响如图14所示。由图14可知,密封盘厚度和过盈量相同时,夹持率越大,清管器与管壁之间的摩擦力越大。密封直板主要以弯曲的形式来适应管道的内径,夹持率的增大提高了直板弯曲变形的难度,因此随着隔离盘直径的增大,摩擦力也会增大。当夹持率从36%增加到42%时,密封直板与管壁之间的摩擦力增加约220 N,而当夹持率从42%增加到48%时,密封直板与管壁之间的摩擦力增加约420 N。这说明密封直板与管壁之间摩擦力的增幅随着夹持率的增大而增大。清管器在实际应用过程中,密封直板的过盈量以及厚度会因为运行过程中的磨损而减小,导致清管器与管壁之间的摩擦力减小,清管效果下降。但是清管器在运行过程中隔离盘的尺寸不会发生变化,因此可以通过增大隔离盘半径的方法来增大清管器与管壁之间的摩擦力。
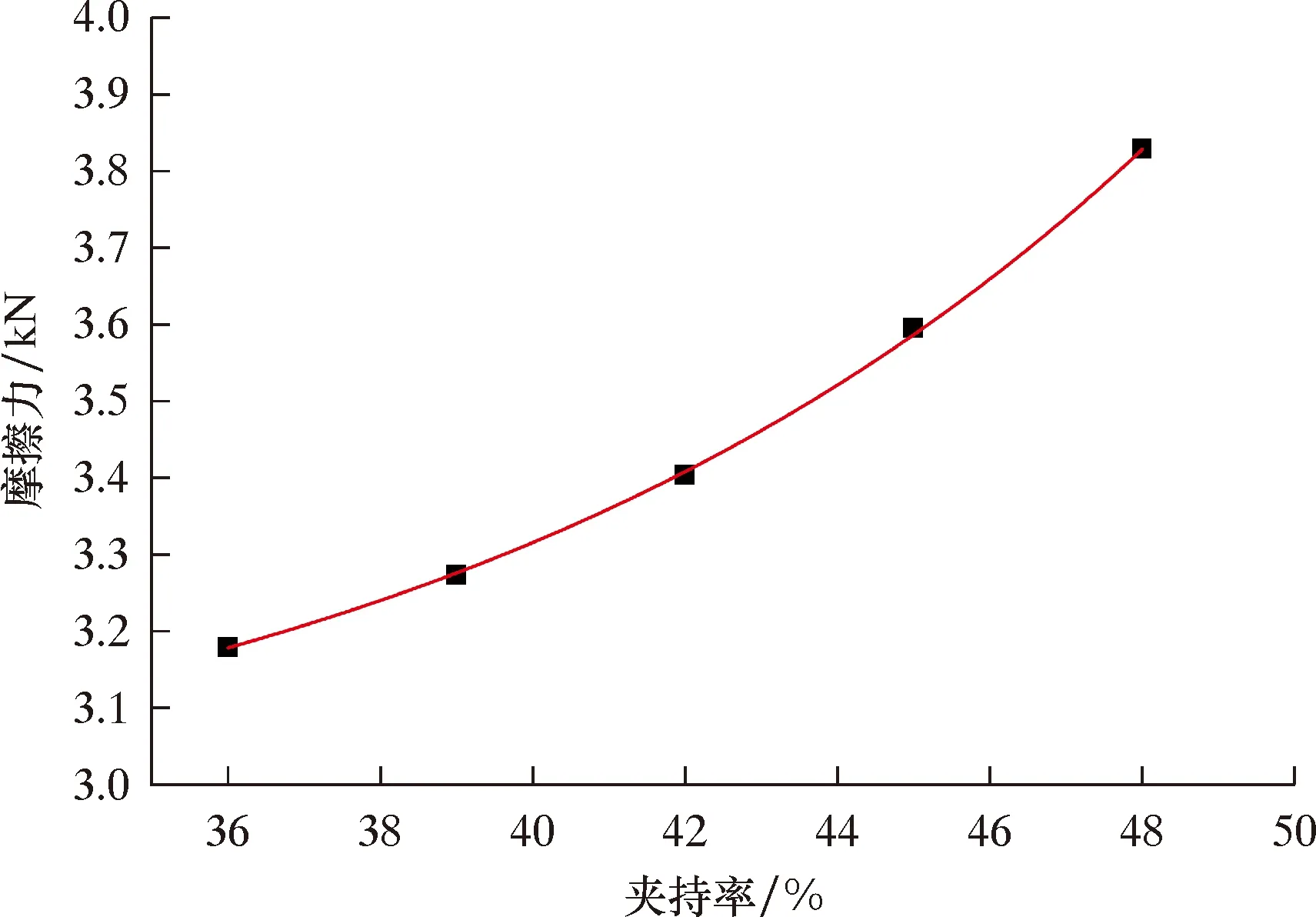
图14 不同夹持率直板对摩擦力的影响Fig.14 Effect of different gripping rates of straight plates on friction force
5 结 论
(1)清管器与管壁间摩擦阻力主要由密封盘过盈产生,基于O’Donoghue皮碗圆弧变形的假设建立了清管器密封直板变形的几何模型,忽略清管器自身重力对摩擦阻力的影响,推导了变形皮碗与管壁摩擦力理论计算过程,以内径317.4 mm的管道为例,得到了直板清管器与管壁间摩擦力的理论计算结果。
(2)基于有限元软件ANSYS建立了直板清管器在内径为317.4 mm的水平管道中运行时的模型,选取Mooney-Rivlin本构方程描述聚氨酯橡胶密封盘应力应变特性,模拟清管器以恒定速度运行的工况。清管器牵拉试验结果与理论计算结果的对比,验证了ANSYS有限元模型作为清管器与管壁之间作用力的计算方法的准确性。
(3)建立了内径317.4 mm的水平管道中直板清管器直板变形的模型,其中直板皮碗的夹持率为40%,厚度为14 mm。通过有限元方法求解得到了不同过盈量下单个密封直板与管壁之间的摩擦力。
(4)研究了直板型清管器不同结构参数(过盈量、直板厚度和夹持率)对清管器与管壁间摩擦力的影响,结果显示清管器与管壁间的摩擦力随过盈量、直板厚度和夹持率的增加而增大,通过调整各个结构参数可优化直板清管器受到的摩擦力。
(5)实际工程中,清管器在运行过程中的磨损会导致清管器的过盈量以及密封直板的厚度减小,使得清管器与管壁之间的摩擦力减小,清管效果下降。由于隔离盘的尺寸在清管器运行过程中不会发生变化,所以可以通过增加隔离盘尺寸的方法来增大清管器与管壁之间的摩擦力。

