考虑河床泥沙淤积的滑坡涌浪数值模拟

王圣浩, 孙 亮, 方卓然, 杨泽旺, 李纪森

(武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063)

0 引 言

滑坡涌浪是峡谷河道中常见的地质灾害,其涌浪带来的次生灾害危害极大[1],开展滑坡涌浪研究对涌浪次生灾害的预测评估具有重要的指导意义。针对滑坡涌浪河道特征的已有研究成果较为丰富。杨飞鹏[2]采用数值模拟方法,研究了断面因素对滑坡涌浪传播特性的影响;王梅力等[3]使用FLOW-3D研究了滑坡体在河道凹凸岸及直线段位置入水对滑坡涌浪周期的影响规律;谢海清等[4]、黄宇云等[5]使用数值模拟方法,模拟分析了狭窄型库区河道的滑坡涌浪产生及传播过程;徐文杰[6]采用数值模拟方法研究了水面宽度因素对滑坡涌浪传播及爬坡高度的影响;徐卫亚等[7]基于分汊河道的分流比理论和经典滑速分析方法,提出了一种计算复杂分汊河道涌浪远场传播的方法;袁晶[8]采用数值模拟方法,建立了可变网格下的一般曲线平面二维滑坡涌浪数学模型,复演了新滩滑坡后某河段的水流形态变化。胡杰龙[9]采用物理模型试验方法,模拟了山区河道型水库滑坡涌浪对不同粒径岸坡最大冲刷深度的影响;任坤杰等[10]通过对不同滑坡体积、滑动面倾角和散体粒径等五种因素进行物理试验,得到了散体滑坡体的首浪高度经验公式。研究结果表明:涌浪传播过程受地形特征影响较大。现阶段对河道中存在泥沙淤积情况下的滑坡涌浪研究较少,实际情况下泥沙淤积一定存在且会对滑坡涌浪造成一定的影响。因此,有必要对河床泥沙淤积情况下的滑坡涌浪进行研究。

本文利用RNGk-ε紊流模型并采用VOF方法对滑坡涌浪进行数值模拟。数值模拟得到的计算值与试验值较好吻合。基于此,模拟了河道中不同淤泥厚度的滑坡涌浪生成及传播过程。研究结果可为实际滑坡涌浪灾害风险评估提供科学依据。

1 数值模拟研究方法

滑坡涌浪为复杂的流固耦合问题。固体需满足牛顿第二定律,流体控制方程为基于连续性方程和不可压缩黏性流体运动的Navier-Stokes方程,即:

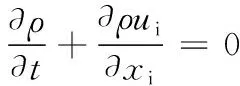
(1)

动量方程:

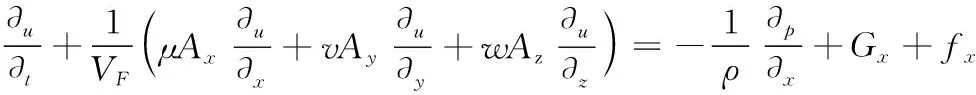
(2)

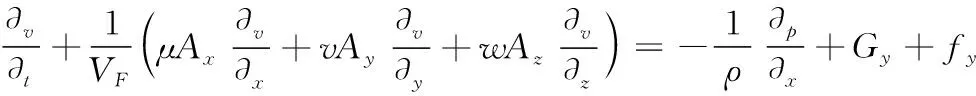
(3)

(4)

式中:ρ为体积分数平均密度;Ax,Ay,Az分别为流体在x,y,z方向单元面内流体可流过区域的面积分数;u,v,w分别为x,y,z方向上的速度分量;VF为单元内流体可流动区域的体积分数;Gx,Gy,Gz分别为流体在x,y,z方向上的质量力加速度;fx,fy,fz分别为流体x,y,z方向上的黏滞力加速度。

本文利用RNGk-ε紊流模型计算涌浪的产生及传播过程,采用有限差分法对控制方程进行离散并采用VOF方法捕捉液体自由表面,该方法仅考虑纯液体单元的影响,在一个网格单元内,所有流体相的体积分数之和等于1。此外,滑坡体采用基于连续体模型基础的颗粒流方法进行模拟。

2 数值模拟方法可靠性分析

根据已有物理模型试验研究成果建立相应滑坡涌浪数值计算模型,对散粒体滑坡涌浪的产生及传播过程进行数值模拟,以验证本文模拟方法的可靠性。

2.1 物理模型配置

Fritz[11]在矩形水槽中对美国Lituya滑坡进行了物理模型试验,水体被指定为海水,密度为1 035 kg/m3,散粒体直径4 mm,滑坡体容重为1.61 t/m3。图1与图2显示了该试验模型基础尺寸与滑坡体初始形态。

图1 美国Lituya滑坡的简化示意图

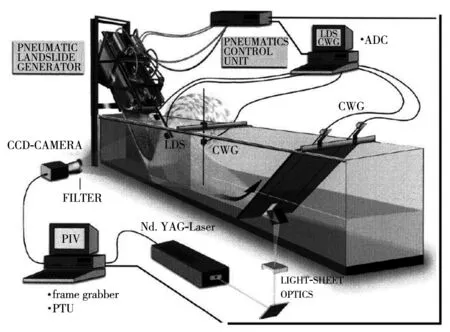
图2 Fritz[11]试验装置示意图

2.2 计算模型及网格划分

根据Fritz[11]的物理简化模型建立了相应的数值计算模型,构建的滑坡涌浪三维模型如图3(a)所示。计算区域均为四边形网格,使用两个网格块覆盖参与计算区域以节约计算资源,网格间距为5 m,网格总数为80万左右,如图3(b)所示。

网格包含的区域为计算区域。两网格块上表面均采用压力边界,底面均为无滑移壁面边界,两网格块交界面会在计算后自动转化为内部网格,交界面上部侧面采用压力边界。

2.3 计算结果对比分析

滑坡体侵入水体后,大量空气夹在滑坡体与涌浪之间,随即破裂产生大量气泡并掺混其中。图4左、右侧分别为数值模拟结果和模型试验的记录结果。同一时刻的流场对比表明,模拟结果与试验记录结果吻合。

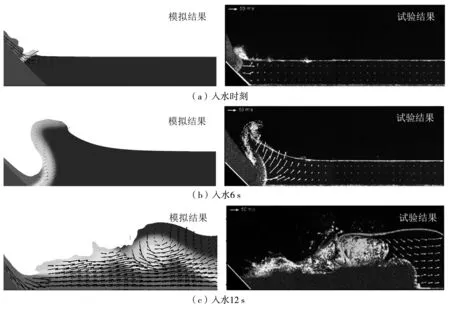
图4 滑坡体入水后不同时刻流速分布图

x=885 m处的涌浪自由表面时程曲线如图5所示。t=20 s时,初始涌浪生成且其振幅达到151 m,与试验结果几乎一致。从曲线的第二个峰值开始,涌浪开始在入水侧岸坡上反复爬坡。由于计算问题的复杂性,涌浪传播方向与爬坡方向的两个波反复叠加,造成后几个涌浪相位出现略微偏差。总的来看,本文模拟结果与试验结果吻合良好。

图5 x=885 m处涌浪自由表面时程曲线

3 河床泥沙淤积滑坡涌浪数值模拟

长江中下游河床泥沙淤积问题突出,且由于其复杂的自然地形条件及频繁的暴雨洪水灾害,极易发生滑坡涌浪灾害。本文选取长江中下游某河段开展泥沙淤积对滑坡涌浪影响的研究。

3.1 计算模型

长江中下游河道宽度在0.8～1.8 km[12],河深一般为8～20 m,洪水期[13]河道流速为1.5～1.7 m/s,某河段河床沉积物主要为中砂和细砂[14]。长江中游各江段泥沙淤积情况在地理上分布不平衡,长江中游各江段的冲淤情况[15]如图6所示。

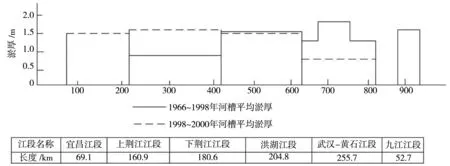
图6 长江中游各江段的冲淤情况模型尺寸

3.2 模型示意图及尺寸

模型设置如图7所示,河道宽度取800 m,两侧岸坡关于河道中央对称布置。右图显示了入水侧岸坡尺寸及滑坡体初始形态。

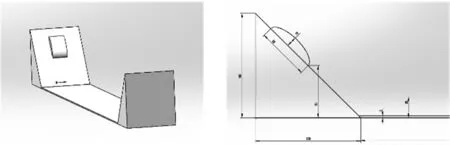
图7 模型示意图及尺寸

3.3 工况设置

根据图6显示的历年淤泥厚度设置工况。淤泥厚度从0 m开始,间隔0.5 m设置一组工况直至2.0 m,共五组。保持河底不透水层至自由表面的高度为8 m,根据各工况淤泥厚度设置相应水深,结果如表1所示。

表1 工况设置(单位:m)

3.4 结果分析

3.4.1 涌浪自由液面

取淤泥厚度为0 m和2.0 m两组极端工况(case1和case5)各监测点的水位时程曲线,如图8所示,用以分析淤泥有无对涌浪高度的影响。

图8 不同位置水位时程图

从图8(a)可以看出,在入水坡脚处,无淤泥工况的涌浪高度达到12.5 m,高于有淤泥工况的8.5 m,差值率达到47.1%,且涌浪波相的衰减随时间出现偏差。

从图8(b)～图8(g)可以看出,随着监测点与滑坡体入水点距离的增加,有淤泥工况的第二次涌浪产生时间会缩短5～10 s,但其涌浪高度几乎保持一致。

总的来说,淤泥对涌浪的影响主要体现在涌浪高度和第二次涌浪的产生时间。

3.4.2 各时刻泥沙形态图对比

图9(a)、图9(b)、图9(c)分别给出了不同时刻的泥沙形态图,左侧为淤泥厚度为2 m的case5,右侧为无淤泥的case1。

图9 各时刻泥沙形态图

从图9中可以看出,入水时刻(t=5 s)x=120 m至x=140 m范围内,左侧已出现明显波峰;滑坡体完全侵入时刻(t=8 s),左侧底部流体向右侧移动较慢,这是由于底部泥沙受到滑坡体冲击与上层水体发生强烈掺混后的密度较大造成的;爬坡时(t=14 s),左侧爬坡高度高于右侧,这是在水体运动速度相同的情况下,沙水混合物密度大,因而具有较大动能造成的。

3.4.3 淤泥厚度为2 m时各时刻流速矢量图

图10中红色代表密度为1 610 kg/m3的滑坡体及底部泥沙,蓝色代表密度为1 000 kg/m3的水。

图10 淤泥厚度为2 m时各时刻密度分布图

入水时刻(t=5 s),滑坡体冲击水体使表层水体产生涌浪向右传播,此时水下滑坡体已受水体扰动而与水体掺混。滑坡体完全入水时(t=7 s),底部混合物密度等值线随涌浪传播形态呈半圆形。

之后(t=10～15 s)滑坡体入水坡脚处的混合物密度传播爬坡过程逐渐达到平衡密度状态。

3.4.4 不同淤泥厚度在x=100 m水位变化及5 s时水位空间分布

图11为不同淤泥厚度在x=100 m处的水位时程曲线。

图11 x=100 m处不同淤泥厚度的水位变化

从图11可以看出,初始涌浪产生的时间随淤泥厚度增加逐渐提前,初始涌浪高度随淤泥厚度增加先减小后增大,具体为:在0～1.0 m范围内初始涌浪高度逐渐减小,在1.0～2.0 m范围内初始涌浪高度又开始增加。其原因可能是由于淤泥厚度与水深比例增大的关系,在达到某一临界值后,初始涌浪高度开始与淤泥厚度成正比。

图12为不同淤泥厚度的最大涌浪高度。

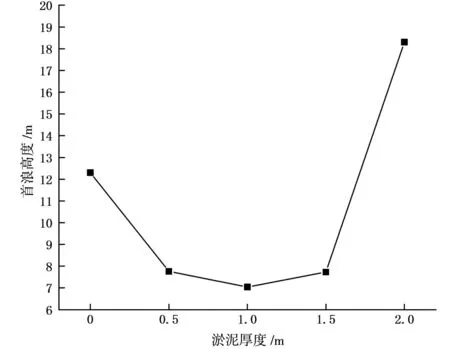
图12 不同淤泥厚度的涌浪高度

从图12可以明显地看出,随淤泥厚度增加,涌浪传播速度降低,在淤泥厚度达到2 m时其速度降低幅值较为明显。

图13为第5 s时的水位断面分布,最小涌浪高度对应的淤泥厚度为1.5 m。

图13 t=5 s时水位分布

因此,在实际河道清淤工程中需适当保留河床泥沙。

3.4.5 不同粒径对涌浪高度的影响

分别按粗砂、细砂、中砂和粉砂的最小粒径0.5 mm、0.25 mm、0.063 mm和0.004 mm[11],设置四组工况,对比不同粒径的泥沙在2 m淤积厚度和8 m水位条件下滑坡体入水处涌浪高度(η)。

滑坡体入水后x=100 m处不同粒径的涌浪高度如图14所示。

图14 x=100 m处不同粒径的涌浪高度

从图14可以看出,不同粒径涌浪高度的差别主要体现在初始涌浪高度,之后的涌浪特征趋向一致。

不同粒径下的最大涌浪高度如图15所示。

图15 不同粒径的涌浪高度

从图15可以看出,涌浪高度与泥沙粒径成正比,粒径越大,涌浪高度越高。

综上所述可知,在易发生滑坡灾害的水域应清理河床表层粒径较大的粗砂。

4 结 论

本文采用RNG k-ε紊流模型与VOF方法对散粒体滑坡涌浪进行数值模拟。与试验数据对比分析,发现本文数值模拟方法具有较高的可靠性。本文的数值模拟方法能较好地模拟散粒体滑坡涌浪产生与传播过程,能对长江中下游存在泥沙淤积的河道提供滑坡涌浪灾害风险参考。

基于长江中下游河道淤积的实际工程背景,本文建立了河道中不同淤泥厚度的数值计算模型,模拟了散粒体滑坡涌浪的产生与传播过程,并分析了初始涌浪的波幅特征及泥沙与水的混合过程对涌浪传播的影响。研究结果表明:

(1) 淤泥厚度对初始涌浪高度的影响较大。

(2) 淤泥厚度对初始涌浪高度的影响存在极小值,实际河道清淤时应保留一定厚度的淤泥。

(3) 所保留的淤泥粒径应尽量小。