拉索钢拱桥吊耳设计及局部受力分析

高鑫崇 田洪泽 陈敬云 蔡保硕 肖翔 吴睿麒

1.北京市市政工程设计研究总院有限公司 100082

2.北京市城市桥梁安全保障工程技术研究中心 100082

3.河北省香河县交通运输局 廊坊065400

引言

拉索钢拱桥因其造型美观，在城市桥梁中得到广泛应用。吊耳做为连接钢拱肋和拉索的关键部件，其安全可靠尤为重要。近些年来，由于吊耳失效造成安全问题时有发生，吊耳的设计和计算成为钢拱桥设计计算中的一个关键节点。现行的《公路钢结构桥梁设计规范》（JTG D64—2015）中并没有对吊耳的计算做出明确的规定。李文治采用了钢结构国标、化工、水利、港口行业标准及有限元方法，对某系杆拱桥吊耳计算方法进行了探讨，研究表明采用国标、化工规范计算结果和有限元方法结论较为接近，而水利、港口规范计算方法较为保守［1］。胡洋采用经典弹性力学方法和有限元方法研究了提篮系杆拱桥的吊耳耳板应力［2］。张牧龙、刘玉贵借助有限元软件对施工吊装吊耳进行了分析计算［3，4］。因此有必要对拉索钢拱桥的吊耳进行局部受力分析，从而有利于掌握其受力特征，为类似工程的吊耳设计提供参考。

1 工程概况

某新建拉索钢拱桥为抱翅型拱-索-梁组合体系，由主拱、斜拉索和主梁三大主体结构组合而成（图1）。拱肋后拱上吊耳采用肋板式吊耳，沿拱肋底板居中布置，吊耳两侧与拱肋隔板焊接（图2）。

图1 某拉索钢拱桥设计图（单位：mm）Fig.1 Design drawing of a cable steel arch bridge（unit：mm）

图2 拱肋吊耳布置Fig.2 Arch rib lifting ear layout

2 吊耳设计

2.1 构造设计

1.规范要求

为防止耳板发生面外失稳，《钢结构设计标准》（GB 50017—2017）第11.6 条［5］对销轴连接的构造做出了规定：①销轴孔中心应位于耳板的中心线上，其孔径与直径相差不应大于1mm；②耳板两侧宽厚比b／t不宜大于4，几何尺寸应符合下列公式规定：

式中：a为沿受力方向，销轴孔边距板边缘最小距离（mm）；be为板件的有效宽度（mm）；b 为连接耳板两侧边缘与销栓孔边缘净距（mm）；t为耳板厚度（mm）。见图3。

图3 销轴连接耳板Fig.3 Pin shaft connecting ear plate

2.尺寸设计

该桥拱肋和吊耳均采用Q420qD 钢板，拱肋为箱型闭合矩形截面，拱肋内设置竖向横隔板及纵向加劲肋。吊耳与横隔板进行焊接，从钢拱肋底板穿出外露40cm 与拉索上吊点连接。耳板和拱肋底板之间设加强板，耳板面外焊接四道加劲板，加劲板外侧与拱肋腹板焊接。吊耳估算尺寸参数如下：t ＝100mm，b ＝300mm，a ＝300mm，详见图4、图5。

图4 吊耳耳板构造（单位：mm）Fig.4 Construction diagram of lug plate（unit：mm）

图5 吊耳示意Fig.5 Schematic diagram of lifting lug

经计算，b／t ＝3.0 ≤4.0，be＝2t+16 ＝216mm ≤b ＝300mm，a ＝300mm ≥4be／3 ＝288mm，可满足防止发生面外失稳的构造要求。本工程钢拱肋吊耳耳销栓孔径边缘距离吊耳的外边缘距离为3 倍的吊耳板厚。结合规范耳板两侧宽厚比b／t 不宜大于4 的规定，建议耳销栓孔径边缘距离吊耳的外边缘距离为3～4 倍的吊耳板厚，可满足规范的构造要求。

2.2 极限承载能力要求

1.规范要求

《钢结构设计标准》［5］第11.6.3～11.6.4 条规定了销轴连接中耳板可能进入四种承载力极限状态，见图6。

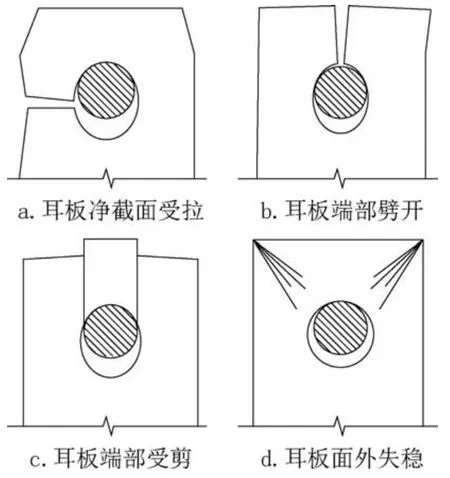
图6 耳板四种极限状态Fig.6 Four limit states of ear plate

连接耳板抗拉、抗剪强度的计算如下：

耳板孔净截面处的抗拉强度：

耳板端部截面抗拉（劈开）强度：

耳板抗剪强度：

式中：N为杆件轴向拉力设计值（N）；b1为计算宽度（mm）；d0为销轴孔径（mm）；f 为抗拉强度设计值耳板抗拉强度设计值（N／mm2）；Z为耳板端部抗剪截面宽度（mm）；fv为耳板钢材抗剪强度设计值（N／mm2）。

2.强度验算

计算采用Q420qD钢材强度设计值见表1。

表1 钢材强度设计值Tab.1 Steel strength design value

通过计算，耳板孔净截面拉应力为98.0MPa，耳板端部截面拉应力为225.1MPa，耳板剪力为69.9MPa，满足《钢结构设计标准》［5］的承载力极限状态计算要求。

3 有限元建模方法

吊耳受力情况较复杂，在拟定完结构尺寸后，需进行建模计算，并对拱肋吊耳局部的受力情况进行分析。本文采用Midas FEA 有限元计算模型进行数值模拟分析，验算在最不利工况荷载作用下，最大索力作用下吊耳及拱肋上相连隔板的受力情况。

3.1 建模范围及有限元离散

模型沿拱肋长12m，包括拱肋顶底腹板、五道拱肋隔板及一处吊耳。采用六面体单元自动网格划分，控制拱肋网格尺寸为20cm，吊耳及隔板网格尺寸为10cm。本模型共47032 个单元，61984 个节点。见图7。

图7 有限元模型Fig.7 Finite element model

3.2 荷载施加

计算模型取索力最大的一段拉索附近的拱肋建立空间实体模型，从桥梁整体计算模型中得出拉索最大索力工况的索力值为4764.1kN，以节点力的形式施加到模型中。

计算模型考虑整体模型中其他段钢拱肋对该段钢拱肋的影响，从整体模型中摘取该段钢拱肋两侧截面内力项，按节点荷载的形式施加在局部模型的两侧截面的节点上。模型边界荷载计算结果如表2 所示。

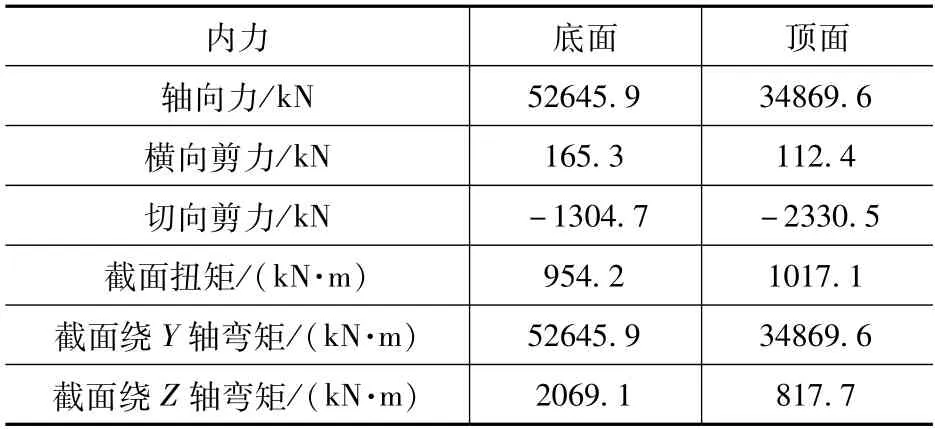
表2 计算模型边界荷载计算Tab.2 Calculation model boundary load calculation

3.3 边界条件

模型的边界条件采用单位荷载刚度法考虑了其他拱肋的刚度影响，在拱肋两侧截面设置弹性约束，弹性支承刚度由整体模型中截面单位力下的位移反算得来。经计算，拱肋两侧截面弹性支承刚度结果如表3 所示。

表3 拱肋边界条件刚度计算Tab.3 Calculation of stiffness for boundary conditions of arch ribs

4 结构计算结果及分析

4.1 计算结果

吊耳耳板的计算云图如图8a 所示。由图可知，吊耳耳板的销轴孔位置mises应力为395MPa，发生局部应力集中的情况，在原设计吊耳的基础上，考虑加厚销轴孔耳板的设计（见图5），并将未加厚与加厚的计算结果进行对比，结果见图8b，局部模型隔板及吊耳计算结果如表4 所示。

表4 隔板及吊耳计算结果Tab.4 Calculation results for diaphragms and lifting lugs

图8 mises 应力分布云图（单位：MPa）Fig.8 Cloud chart of mises stress distribution（unit：MPa）

4.2 计算结果分析

1.有限元应力计算结果分析

销轴孔耳板未加厚时，应力集中处吊耳mises应力为395.3MPa，最大剪应力为212.6MPa，均超出Q420qD钢材的强度设计值；销轴孔耳板厚度加厚50%之后，应力集中处的mises应力为292.4MPa，最大剪应力为163.3MPa，应力降低了30%～35%，改善效果明显。吊耳大部分区域mises应力范围在30MPa～230MPa 之间，最大剪应力范围在16MPa～120MPa 之间，与加厚销轴孔耳板前的计算结果相近。横隔板和吊耳加劲板的mises 应力在加厚销轴孔耳板之后减小了8%～19%，最大剪应力减小了18%～25%。加厚销轴孔耳板后的mises 应力、最大剪应力均满足《公路钢结构桥梁设计规范》［7］规定的Q420 钢材强度设计值。

2.有限元与规范计算结果对比分析

有限元计算结果与按《钢结构设计标准》［5］11.6 条计算结果对比如表5 所示。

表5 有限元计算结果与规范计算结果对比Tab.5 Comparison of finite element calculation results with standard calculation results

由表5 可知，有限元方法和规范方法计算的耳板端部截面拉应力和耳板剪应力结果较为接近，耳板孔净截面拉应力有限元计算结果比规范计算结果更为不利，同时有限元计算结果可以更全面地体现出吊耳耳板任意位置应力。可见，在受力复杂的吊耳设计计算中，采用有限元计算方法是有必要的。

5 结语

1.在现行的《公路钢结构桥梁设计规范》中没有吊耳设计应满足的构造要求，但是在国家标准《钢结构设计标准》中提到了销轴连接应满足的构造要求，拱肋吊耳的设计中应予以参考。结合本文计算结果及国标中销轴连接构造要求，建议耳销栓孔径边缘距离吊耳的外边缘距离为3～4 倍的吊耳板厚。

2.局部有限元模型边界条件的模拟是建模的重点，考虑到拱肋其他部位对局部有限元模型的刚度影响，本文采用单位荷载刚度法，即在局部模型对应的整体杆系模型的分界处施加单位荷载，通过单位荷载产生的位移反算出截面的支承刚度，局部模型中拱肋两端截面设置节点并施加对应的弹性约束。

3.本工程吊耳耳板孔周围钢板加厚50%，应力可降低30%～35%。加厚吊耳耳板耳环可以有效缓解局部计算模型中吊耳销栓孔处的应力集中。

4.有限元计算可以更全面地体现出吊耳耳板任意位置的应力，其计算结果比规范计算结果更为不利。在吊耳设计计算中采用有限元计算方法是有必要的。