语义解悖方案及其对辩证逻辑的启示

姚从军，贺春雅，邢万成

（1.湘潭大学哲学系，湖南 湘潭 411105；2.四川大学哲学系，四川 成都 610065）

一、典型语义解悖方案及其困境

语义悖论的出现最早可以追溯到古希腊时期，说谎者悖论常被学界视为典型的语义悖论[1]。众多优秀的逻辑学家对以说谎者悖论为代表的语义悖论提出了众多创新性的解悖方案，包括但不限于罗素类型论语义解悖方案[2]、塔尔斯基语义论语义解悖方案、克里普克真理论语义解悖方案[3]690-716、语境迟钝主义语义解悖方案和语境敏感主义语义解悖方案，等等。上述语义解悖方案大都持拒斥悖论的态度，面临各种各样的困境，即不符合解悖标准RZH解悖原则的要求[4]34。

(一)罗素类型论语义解悖的困境

罗素类型论分为简单类型论和分支类型论。简单类型论通过“类”进行分层，确定意义的不同层次来解决悖论。而分支类型论借助恶性循环原则[4]49，采用命题函数分阶来进行更为复杂的划分。何为恶性循环原则？即“凡涉及一个汇集全体分子的事物，都不是该汇集的分子[5]。”根据恶性循环原则，每一级的性质都不能以该级性质的总体或更高级中的性质定义来确定。[4]51通过分级和限制条件，从而避免恶性自指，有效解决悖论。

但罗素类型论自身仍存在两个缺陷，即“可化归性公理”及“恶性循环原则”。按照分支类型论的层次划分，系统将会排除掉很多合理的东西，数学中很多有益的基本数学概念将被排除。为避免排除过多，罗素引入可化归公理：在给定的类型内每一个非直谓定义都有一个与之等价的直谓定义。[6]但这条公理的引入，除了能保留一些重要的数学定理以外，让人极其难以接受。从语义悖论来看，分层理论不能很好地应用在一些具体的语义悖论之上，在自然语言中，很难找到与非直谓定义相对应的直谓定义。可化归性公理和分层理论不可兼得，引入可化归公理必然削弱“恶性循环原则”的效力。罗素后期在自我反思逻辑类型论时，也放弃了可化归性公理。类型论面临的问题是：如何在避免非直谓定义的限制下构建满意的数学形式系统？类型论的局限源于其依赖的悖论解决机制，利用恶性循环原则和分级理论必然会导致放弃一部分理性的数学表达，由此只能在部分领域解决悖论。

（二）塔尔斯基语义论语义解悖的困境

塔尔斯基从说谎者悖论出发，提出了T 模式，即“X 是真语句当且仅当p”。通过T 模式构建出真理概念的意义，并通过这个模式来解决语义悖论。作为真理概念的T 模式并不能单独解决语义悖论，并且T模式本身被视为是产生语义悖论的一个重要原因。语义悖论产生的根源在于语言的语义封闭性，承认经典逻辑规则必然接受语义封闭的条件，而解决悖论的方法就在于把语义封闭变为语义开放。塔尔斯基认为，给语言划分层次就能使得语义具有开放性。语义开放需要借助两种不同的语言来实现。两种语言存在着不同的性质：第一种是对象语言，即“被谈及”的语言，是用于讨论的，在系统中存在的形式素材或语言符号；第二种是元语言，即用来“谈及”对象语言的语言。两种语言之间具有相对性，一定程度上可以相互转换。

塔尔斯基语义论中的“语言”都是指“形式语言”。[7]塔尔斯基认为将自然语言改造成可以分层的形式语言必定是“徒劳”的，因为自然语言庞大的数量使得只能截取一部分自然语言进行形式刻画，这就显示出语义论的第一个困境，无法对所有自然语言的悖论进行有效地解决。塔尔斯基的“语义封闭性”观点将导致自然语言悖论无法解决。一个好的语义解悖方案不仅需要构建刻画自然语言的合理方法，而且需要给出非特设性哲学说明。而语义论的第二个困境在于它的强特设性，即不能给解悖方案提供一个高度合理的哲学说明。“真”在自然语言中本是单义的，然而通过分层思想把真值概念分裂成无穷多的谓词常项，违反人们的日常思维和直觉，这种层次建构具有强烈的特设性。真理概念尽管在语义悖论中很难定义，但其作为一个经验事实在自然语言中是可表达的。语义论第三个困境就在于其真理概念的分层问题，自然语言中很难完成元语言和对象语言的分层关系。语义论解悖方案对语义悖论的无能为力，注定了解决语义悖论，还是得回到自然语言之中。

（三）克里普克真理论和语境迟钝主义语义解悖的困境

在《真理论论纲》中，克里普克曾对类型论和语义论进行了评价，类型层级和语义分层禁止出现自我指称或包含其自身真值谓词的语言。[3]690-716而实际上不应存在这种禁止，因为自然语言中也可以在不避免自指和不分层的前提下去谈论自身的语义。克里普克的成果在于他坚持回归自然语言的研究思路，提出以“根基”为核心的真理论解悖方案。克里普克在以往的语义解悖方案的局限中意识到，既要解决类型论恶性循环的困境，又要避免语义论强特设性的局限，就需要一种能明确真值谓词单义性的理论。这种理论只要求部分定义真值谓词，允许真值谓词存在“间隙”，即有公式既非真又非假，处于一个空缺的状态。语义悖论被划分到真值间隙，从而将其避免和解决，这样就能保证在维持系统相容性的前提下，同时满足自然语言语义封闭的日常直觉。

不难肯定真理论语义解悖方案的突出贡献，但此方案也存在着种种困境。首当其冲的是无法合理地说明强化的说谎者悖论。强化的说谎者悖论指“本语句或是假的或是真值间隙的”这样的语句。任何突破二值逻辑的语义解悖方案都将面临此问题：把“真值间隙”作为第三个真值则会使得悖论陷入困境，从而“跳出油锅又进火坑”。作为一种含有特殊的真值间隙语义解释的真理论语义解悖方案，将同样会面临强化的说谎者悖论难题且无法解决。其次，克里普克没有提出一个清晰的标准来区分本真态的自然语言和作为元语言的自然语言，而这种区分是很难找到界限的。再者，真理论方案的另一缺陷在于无法在形式语言中合理表达经典逻辑规则。逻辑学家古普塔在《真理与悖论》中对这一缺陷进行了深入分析。[8]古普塔首先肯定了克里普克的观点，认为在形式语言中可以存在自指。例如“所有句子或真或假”。因自然语言符合日常直觉，该语句都应该接纳自指并必定为真的。然而，古普塔却指出真理论方案却不能有效处理这类语句，这种表述逻辑法则的句子在形式语言中的任何定点都没有真值，并且此语句是悖论性并处于真值间隙，因此背离了重要的日常逻辑直觉。古普塔提出了经典的“经验反例”，并指出如果我们把最小固定点作为真理模型，那我们将不可避免地产生新矛盾。

语境迟钝主义解悖方案以赫兹伯格的“素朴语义学”方案和古普塔的“真理修正程序”方案为代表，均是对克里普克真理论的改良，以“素朴语义学”为例，其并未真正克服真理论方案的局限：第一，此方案依旧需要在自然语言中追求一种并不存在的元语言，并且难以合理地进行表达；第二，依旧无法处理强化的说谎者悖论，依然无法合理地刻画自然语言语义封闭的本真态。语境迟钝主义并未真正克服真理论的困境，是否存在一个真正刻画自然语言的语义封闭性同时不必上升到元语言的形式理论，依旧是语义解悖的难题。

（四）语境敏感主义语义解悖的困境

语境敏感主义是关注在语句中语境对真值变化起本质作用的语义解悖方案。就语义悖论而言，“语境”与语言的认知意义相关，伯奇的《论语义悖论》被普遍视为语境敏感主义解悖方案的起源。[9]伯奇认为真理论语义解悖方案的困境在于，在语言中追求一个具有固定外延并可以赋予任何部分真假的单一性真值谓词。而在语句中引入“语境”，让真值谓词的外延发生变化，就能克服真理论局限。在伯奇看来，在语境影响下的真值谓词具有单义的索引性，语境变化可以让真值谓词指谓不同的外延，相同的语句普型可以有多个不同真值的语句殊型。通过这样的处理，就能轻松解决语义悖论中典型的说谎者悖论。不同的语句殊型解释决定了伯奇型语句真值外延的变化。语境敏感主义相较于真理论的优势在于可以在形式技术上比较圆融地处理强化的说谎者悖论。但在哲学说明上却遭受到很多质疑，根本原因在于其特设的真值谓词的索引性被诉诸为自然语言中体现的素朴直觉，缺乏足够的说服力。

巴威斯是伯奇的后继者，赞成其观点并在其基础上提出了情境语义学解悖方案。为了克服伯奇方案的局限，巴威斯转而在情境语义学中创新性地增加了情境参量，从而建构一种带有单义的、非索引性真值谓词的语境敏感主义解悖方案。[10]这种新型的“革命性”的观念自出现之时起就遭到广泛质疑与反对。情境语义学解悖方案的优势在于其哲学说明，从而具有真正的“非特设性”。情境语义学坚持“语言效应论”，指在不同的主体、空间和时间中，相同的语句可能会产生不同的解释。情境语义学相较于伯奇方案，其优势在于坚持真值谓词本身不是索引性的，而是符合自然语言常识的，并且可以在同一意义上使用的非索引性谓词。情境语义学的困境主要集中在形式系统的构建上。[11]相对于伯奇方案，情境语义学解悖方案的优越性本来就不是在形式技术方面。[12]语境敏感主义的两大语义解悖方案，要么在形式技术方面没有完备的理论，要么缺乏足够合理的哲学说明，这两点都不符合RZH解悖标准的要求。

不同于典型语义解悖方案，次协调逻辑语义解悖方案被视为新型的语义解悖方案。之所以被称为新型解悖方案，这是因为次协调逻辑不再尝试消解悖论，而是将悖论合理的纳入现有的知识体系之中。次协调逻辑语义解悖方案应运而生的，根本原因在于悖论无法被一劳永逸地解决。

二、次协调逻辑的“真矛盾”探究

普利斯特是最早将次协调逻辑思想引入语义解悖的学者，并形成其独特的次协调逻辑语义解悖方案，即“次协调逻辑”。典型的语义解悖方案均坚持经典逻辑，坚持语义协调性，即出现悖论和矛盾的系统都是不协调且琐碎无用的系统，其核心观点都是致力于在经典逻辑体系下解决语义悖论，将矛盾和悖论从一切逻辑系统中排除出去，从而建立协调且无矛盾的形式系统。而次协调逻辑语义解悖方案则采取与排除悖论截然不同的解悖思路。在普利斯特的《次协调逻辑》中，他的核心思想便是把真正的严格悖论当作“真矛盾”来接受，并在形式技术上将之“圈禁”起来，以堵塞其“有害的灾难性扩散”的途径。[13]219-241次协调逻辑尝试将悖论纳入到已有的科学知识体系之中，因而与其他经典的语义悖论解决方案有着本质的区别。在他的另一本著作《走进矛盾》中[14]，普利斯特完成了以“真矛盾”概念为核心的次协调逻辑解悖体系，使得次协调逻辑语义解悖方案在形式系统和哲学说明方面取得了较大的进步。

普利斯特把次协调逻辑的形式系统称之为LP。LP 是一个允许真矛盾的次协调逻辑系统，并通过一种合理的方式接纳悖论于系统之中。LP的创新不仅在于给出一个形式系统，与前人的区别在于给系统的形式符号赋予一种直观且合理的语义解释，从而丰富了次协调逻辑系统的语义和句法。在次协调逻辑系统中存在三个真值，除了经典逻辑中的单真和单假以外，增加一个真值“悖论”，即一个句子既真又假。单真性质记为“t”，单假性质记为“f”，矛盾的性质记为“p”。这样一来，我们就要重新定义经典逻辑中的命题联结词，包括¬、∧、∨、→、，以此来构建一个命题联结词集合。同时继承经典命题逻辑中真假的相互转换，即对真的否定是假的，对假的否定是真的，再增加一条：对悖论的否定仍然是悖论的。由此我们可以得到一个新的关于命题联结词的真值表，如下表格所示：

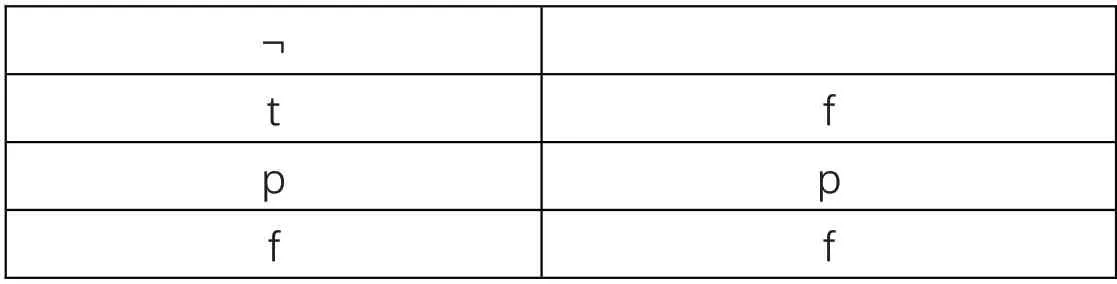
表1 ¬的真值表

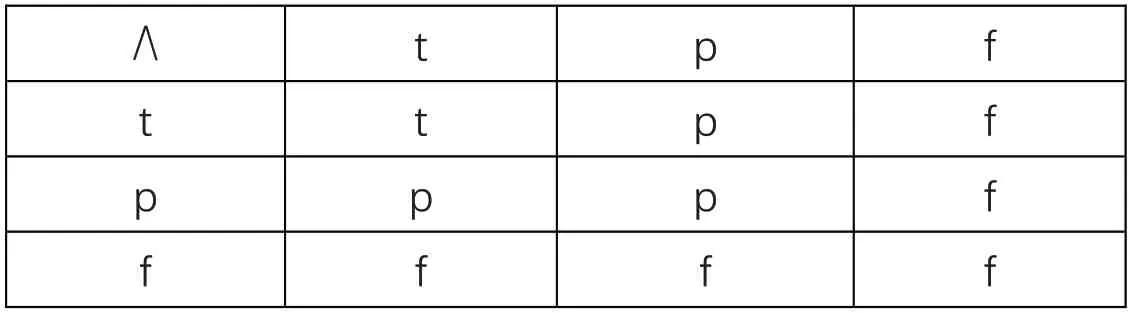
表2 ∧的真值表

表3 ∨的真值表

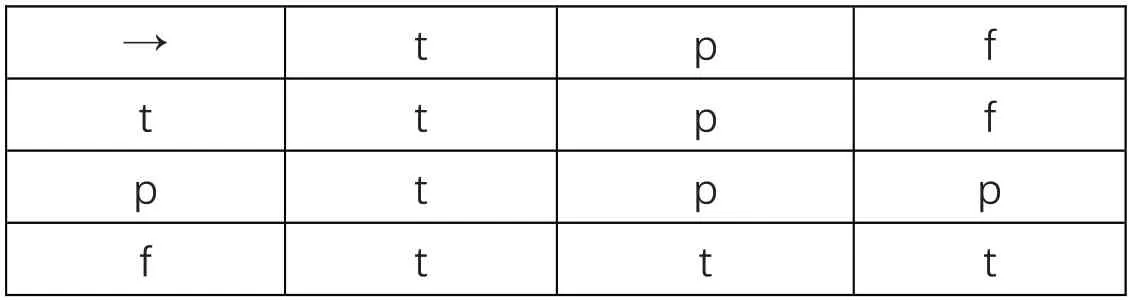
表4 →的真值表

表5 →→的真值表

符号的某些定义与经典逻辑相同，例如：A∧B等价于¬（¬A∨¬B），A→B被定义为¬A∨B，等价于A→B∧B→A，等等。但也有一些符号定义与经典逻辑不同，例如：当A是真的，B是悖论的，合取A∧B 为真；当A 或B 为假时，合取A∧B 仍为假；当A 或B 中有一个是悖论的，析取A∨B 则为悖论的。有了这些逻辑常项的定义，我们可以定义出LP的形式系统。[13]219-241

在形式上，令L为一个命题语言，其命题变量集为P。设v：P→{t，p，f}，即v是命题变量的赋值。设v′是v的自然延伸，它给L中的合式公式赋值。若Σ是L中语句的集合，我们有这样的定义：

Σ⊨A当且仅当没有一个v满足v′（A）=f，但对于所有的B∈Σ，v′（B）=t或p；

（⊨意为语义蕴含）

⊨A当且仅当Ø⊨A（即对于所有的v，v′（A）=t或p）。

根据上述的符号和定义，LP有如下定理：

（1）A ⊨A∨B

（2）A,B ⊨A∧B

（3）A→B ⊨¬B→¬A

（4）A→(B→C)⊨B→(A→C)

（5）A ⊨B→A

（6）¬A,¬B ⊨¬(A∨B)

（7）¬A→¬B ⊨B→A

（8）¬(A∨B)⊨¬A

（9）A ⊨¬¬A

（10）¬¬A ⊨A

（11）¬A ⊨¬(A∧B)

（12）¬(A→B)⊨A

（13）A∧B ⊨A

（14）A,¬B ⊨¬(A→B)

（15）A→B ⊨A∧C→B∧C

（16）¬A ⊨A→B

（17）A→(A→B)⊨A→B

（18）A→¬A ⊨A

上述都是有效式。此外，很容易发现一些推演是不成立的，如：

（1）A∧¬A ⊨B

（2）A→B，B→C ⊨A→C

（3）A,¬A∨B ⊨B

（4）A,A→B ⊨B

（5）A→B,¬B ⊨¬A

（6）A→B∧¬B ⊨¬A

有了上述符号、定义和定理组成的LP系统，我们很容易从LP扩展到量化逻辑系统LPQ。令L′为一阶语言，为了简单起见，我们假设它没有常项和函数符号。

设A=，D是一个对象域。如果Pn是形式语言L′的一个n元谓词，并且x′是D的n元组成员，I是到{t，p，f}的映射。[13]219-241令S是LP中的变元指派，即变量集到D的映射。LP的公式在指派S下的真值定义如下：

如果A 是形如Pn（vi，...，vn）的公式，那么A 是或t 或f 或p 的，因此I(Pn）()也是或t 或f 或p的。

如果A的形式是¬B或B∧C的，那么A的真值条件可以参考LP中的真值矩阵。

如果A是形如（∀v）B，则A为t当且仅当对于所有的d∈D，B在S(v/d)替换之下为真；A为f当且仅当有d∈D，B在S(v/d)替换之下为假；A是悖论的当且仅当对于所有d∈D，B在S(v/d)替换之下或是真的或是悖论的，并且存在d∈D，B在S(v/d)替换之下是悖论的。

可以证明，如果A是一个封闭的公式，那么A的真值与我们选择的S无关。

如果Σ是L′的语句集，我们定义：

Σ⊨A当且仅当，没有一个S满足对于所有的B∈Σ，B在S下是真的或悖论的且A在S下为假。

LPQ拥有和LP中相似的定理。跟LP系统一样，我们有一些正确的演绎推理关系，如下：

（1）（∀x）A,（∀x）B ⊨（∀x）(A∧B)

（2）（∀x）A ⊨¬(Ex)¬A

（3）（∀x）A ⊨（∀x）(A∨B)

（4）（∀x）(A→B)⊨（∀x）A→（∀x）B

（5）（∀x）A ⊨A（x/y）

（6）（∀x）A ⊨（∀x）(B→A)

（7）（∀x）(A→B)⊨（∀x）(¬B→¬A)

（8）（∀x）A ⊨（∀x）(¬A→B)

（9）（∀x）(A→B)⊨(Ex)A→(Ex)B

此外还很容易发现，一些模式不再成立：

（1）（∀x）A，（∀x）(A→B)⊨（∀x）B

（2）（∀x）(A→B)，（∀x）¬B ⊨（∀x）¬A

（3）（∀x）(A→B)，（∀x）(B→C)⊨（∀x）(A→C)

定理（等价替换）假设A、A′有变量y1，...，yn，并且B′与B相似，只是B′包含A′，而B包含A，则有：

（∀y1，...，yn）（A«A′）⊨B«B′

证：此结论通过B的归纳而形成。如果A是B，那么结果如下，因为（∀y）C ⊨C。如果在构造中使用真值函数，则使用以下规则来确定结果：

如果在结构中使用了量词，那么结果遵循这两条规则。

如果A⊢B，并且x不在A中自由出现，则A ⊨（∀x）B并且（∀x）（AB）⊨（∀x）A（∀x）B。证明完毕。

有了上述定义，形式系统LP和LPQ及其语义解释就变得清晰起来。

三、次协调逻辑的哲学思想、创新之处及其对辨证思维研究的启示

接下来谈谈次协调逻辑的哲学思想。首先，说明真矛盾的性质。在次协调逻辑系统之中，悖论成为“有意义的矛盾”，指在形式系统内可以合法存在，且不能从矛盾推出一切，即不会导致系统不足的“矛盾”。悖论是可以进行改造并加以接受的“有意义的矛盾”。普利斯特将形如A∧¬A的矛盾称之为“真矛盾”，将能够容纳“真矛盾”的次协调逻辑系统则被称为“真矛盾论”。其次，次协调逻辑系统对矛盾律进行削弱。矛盾律作为经典逻辑的根本法则之一，决定了命题不能同时既真又假，但次协调逻辑系统却改变了这一规则，在面对悖论时，允许有些语句同时兼具真假性质，而在面对非悖论性语句时，矛盾律在次协调逻辑系统中依旧有效。作为一种非经典的语义解悖方案，次协调逻辑系统认为矛盾律对悖论式语句失效，换言之，矛盾律只是准有效的。第三，次协调逻辑系统限制从假命题和矛盾推出一切。在经典逻辑中，我们有实质蕴涵怪论，即真命题被一切命题蕴涵，假命题蕴涵一切命题。[15]188次协调逻辑系统则关注假命题推出一切这一部分。在经典逻辑系统中矛盾被视为永假式，而以永假式为前提必然可以推出一切命题。当经典逻辑视矛盾为假时，包含矛盾的系统也必定是无意义的。为了避免系统变得无意义，次协调逻辑系统限制了这一点，即某些假前提并不能推出一切，这里的假命题并非所有的矛盾，而仅仅是真矛盾这样的前提，因为真矛盾并不在次协调逻辑中预设为假。在不包含真矛盾时，仍保留这一规则，即假命题推出一切。

相较于典型语义解悖方案而言，次协调逻辑语义解悖方案的创新之处主要体现在三个方面。第一，超越了分层理论的限制和预设的强特设性局限。次协调逻辑没有借助于分层理论来解决语义悖论，故因分层而导致的语义解悖困境将不复存在。通过引入第三值“悖论的”，并且视其为与真谓词同等地位，这样将对大部分的自然语言进行一个划分，所有的自然语言语句除了真假性质之外，所有的悖论性语句都被划入了悖论类型，这就合理解决了所有的自然语言悖论，由此在不需要区分元语言和对象语言的情况下有效地解决了语义悖论。第二，次协调逻辑能够有效地解决强化的说谎者悖论。所谓强化的说谎者悖论就是形如“本语句或是假的或是真值间隙的”，真理论和语境迟钝主义都无法解决这种强化的说谎者悖论。在次协调逻辑中，强化的说谎者悖论语句可以被改写为“本语句是假的或是悖论的”。次协调逻辑对这种语句的解释的创新之处在于，将“悖论的”视为一种真谓词，并且和真谓词具有相同地位，这样就能构成一种等价，从而有效地克服强化的说谎者悖论。第三，次协调逻辑兼具形式技术和哲学说明，在形式技术上，提出形式系统LP和LPQ。一方面，在解决原有说谎者悖论的同时，并未产生新的不可解的强化的说谎者悖论；另一方面，LP和LPQ是在经典逻辑的基础上构建的，很大程度上保留了经典逻辑的规则和定理，将涉及悖论的规则视为次有效的。在不涉及悖论时，这些规则仍具经典逻辑的有效性。在哲学说明上，次协调逻辑说明了需要接纳悖论的理由。次协调逻辑对悖论的认识继承了塔尔斯基的观点，即认为语义封闭的理论都是不一致的。而自然语言在形式上都是封闭的，因此自然语言必然包含悖论。同时，次协调逻辑继承了康德和黑格尔认为悖论先天存在于语言的观点，由此说明了悖论为什么无法解决。正因为次协调逻辑既可以克服以往语义解悖的局限，又能兼具形式技术和哲学说明两大优势，由此可以认为，以LP和LPQ为代表的次协调逻辑语义解悖方案对以往典型语义解悖方案的困境有了明显的突破。

次协调逻辑语义解悖方案对辨证思维（即辨证矛盾）的研究具有较大的借鉴意义和启示作用。从关注辩证思维现象的角度看，标注逻辑把原子公式句法层面的矛盾转移到语义真值格，使得由标注原子公式pλ构成的矛盾命题“pλ∧¬pλ”是可满足的，而由复合公式F构成的矛盾命题“F∧¬F”是无效的，这就限制了矛盾的扩散。量化动态逻辑QDL源于对计算机程序语言中程序更新的描述。静态看，程序语言的循环赋值语句“i=i+1”的句法表层是矛盾的。然而，QDL的赋值函项序对〈a,b〉表示b对a进行更新，即b 对等号左边i 的赋值可以不同于a 对等号右边i 的赋值，句法表层的矛盾在语义层面得到化解。近年来，杜国平教授创立的哲思逻辑通过经典否定~和算子*的叠置定义了“直觉主义否定”△和“次协调否定”△，试图揭示“辩证矛盾”和辩证推理A→*A，并中采用这样的辩证推理来解读辩证思维的否定之否定规律。如辩证思维的否定之否定表述为：正题A ⇒反题~A ⇒合题△~A（即*A）或正题A⇒反题∇A ⇒合题~△A（即*A）。合题呈现的双重否定△~A或~△A（即*A）不等于正题，合题是辩证思维螺旋上升的结果，形式化地刻画了辩证思维的否定之否定规律。[16]

四、次协调逻辑语义解悖方案对辩证逻辑的启示

次协调逻辑语义解悖方案对于辩证逻辑的启示主要体现在悖论的性质归属、辩证逻辑的性质归属、辩证逻辑形式系统构建等三个方面。

首先，次协调逻辑语义解悖方案有力地证明了悖论是一种特殊的辩证矛盾。从次协调逻辑的视角出发，笔者对悖论的性质归属问题的答案，倾向于认为悖论是辩证矛盾。次协调语义解悖方案接纳的受，普利斯特所提出的的真矛盾具有双面真理的性质，即悖论作为一种真谓词被系统合理接受。次协调逻辑中的悖论就具有了辩证矛盾的性质。在这种对悖论态度的转变中，显示了悖论性质转变的可能。对于悖论性质的认识关键在于对悖论本体论的认识，即悖论能被消解还是不能被消解。典型语义解悖学家坚持悖论能被消解，因此很容易地判断出悖论是逻辑矛盾。而在次协调逻辑学家看来，悖论不能也不应被消解，而是存在于系统内部的一种真矛盾，而且可以合理地存在于系统之中，这种矛盾具有辩证性，因此悖论被视为辩证矛盾。

其次，次协调逻辑语义解悖方案有效解决了辩证逻辑属于哲学还是属于逻辑的学术争议问题。从次协调逻辑视角出发，认为辩证逻辑兼具哲学和逻辑的双重性质。辩证逻辑的学科性质问题，是辩证逻辑发展过程中的理论问题。[17]了解辩证逻辑的性质问题，可以促进辩证逻辑的深入发展。关于辩证逻辑是哲学还是逻辑，学术界也常有争议。主要存在三派学术观点：第一派认为辩证逻辑是哲学，即认为辩证逻辑的研究内容是思维的辩证法，具有深刻的唯物辩证法属性；第二派认为辩证逻辑是逻辑，即认为辩证逻辑研究辩证思维形式、规律和方法；第三派认为辩证逻辑既是哲学也是逻辑。辩证逻辑的哲学性体现在其作为逻辑的辩证法，是马克思主义哲学的研究领域之一；其逻辑性在于其研究对象仍是思维的规律、形式和方法并以形式逻辑为基础进行形式化研究。笔者支持第三派的学术观点。次协调逻辑关于真矛盾和削弱矛盾律的部分与辩证逻辑对立统一的规律相吻合，包含着对立统一等辩证法的性质，因此必然带有哲学性。次协调逻辑是在形式逻辑基础上加上辩证法而形成的，因此同样具备逻辑的特征。所以，次协调逻辑深刻体现着辩证逻辑的哲学和逻辑学的双重性质。

最后，次协调逻辑语义解悖方案为辩证逻辑建立形式系统提供了思路。次协调逻辑是辩证逻辑形式化的经典途径之一，而普利斯特的次协调语义解悖方案——悖论逻辑则是辩证逻辑形式化的又一次具体的尝试。次协调逻辑和辩证逻辑之间有着密切的联系。次协调逻辑学家达科斯塔曾提出“一条双行道，其中每一领域都显示了另一领域的可能性”[18]，以此来说明两者的联系。普利斯特在《走进矛盾》中引用黑格尔辩证逻辑的观点作为开头和结尾，也表明了次协调逻辑和辩证逻辑密切的联系。[15]299-302次协调逻辑语义解悖方案有力地支持了辩证逻辑的形式化，辩证逻辑本质上是一种非经典逻辑。次协调逻辑取消了不矛盾律和司各脱规则的普适性，限制其适用范围，区分有意义的矛盾和无意义的矛盾。在国内，我国学者赵总宽团队、桂起权和陈自力团队、马佩和张金成等学者针对辩证思维也构造了一批辩证逻辑系统，这些系统在一定程度上揭示了辩证思维的部分逻辑特征。以桂起权[19]为代表的弱辩证逻辑学派借助次协调逻辑思想来完成辩证逻辑的形式化，认为不矛盾律等经典逻辑规律不再普遍有效，是辩证逻辑研究的积极探索者。

综上所述，次协调逻辑语义解悖方案从哲学和逻辑两个方面为辩证逻辑增添了新的内容，带来了新的启发。在哲学方面，次协调逻辑为辩证矛盾和辩证逻辑的性质提供了有力的哲学说明，增加了辩证逻辑非形式化的研究范围。在逻辑方面，次协调逻辑为辩证逻辑形式化提供了一种行之有效的思路，建立了以真矛盾为核心的辩证逻辑形式化体系，合理地将辩证矛盾接纳到形式系统之中。