快速二维累积剩余Tsallis 熵阈值分割方法

黄 聪，邹耀斌*

（1.三峡大学 水电工程智能视觉监测湖北省重点实验室，湖北 宜昌 443002；2.三峡大学 计算机与信息学院，湖北 宜昌 443002）

1 引 言

阈值分割因其高效、易于实现而被广泛应用于工业缺陷检测［1］、SAR 图像目标识别［2］和目标检测［3］等诸多实际领域。根据所使用直方图的维度，现有阈值分割方法可以分为一维灰度直方图阈值法［4-6］和二维灰度直方图阈值法［7-9］。一维灰度直方图阈值法没有考虑像素间的空间相关性，只要图像的一维灰度直方图相同，即使图像的内容不同也将产生相同的分割阈值［10］。二维灰度直方图阈值法由于综合考虑了像素自身及其空间邻域信息，总体分割结果优于对应的一维灰度直方图阈值法。然而，受制于空间邻域信息的构造或者阈值选取的目标函数，不少二维灰度直方图阈值方法仅限于分割直方图呈现双峰模式的图像，并且计算效率相对较低。

为了克服二维阈值方法的上述局限性，近些年，研究人员提出了一些针对性的改进方法。陈琪等提出了改进的二维Otsu 法及其快速实现［11］，吴一全和潘喆则提出二维Tsallis 熵法的快速递推算法［12］，这两个方法将时间复杂度降为O(L2)（L为直方图的最大灰度级）。然而，它们在设计快速递推算法时仅考虑对角区域像素而忽略了边缘像素的影响，所得分割阈值容易偏离理想阈值。赵恒等［13］通过边缘信息拟合曲线重新对二维直方图进行分区，提出了双曲线二维Otsu 法，在分割精度和抗噪方面都有所提升。梁义涛等［14］结合二维Otsu 折线法和曲线拟合方法提出一种改进的二维Otsu 拟合线法，在某些边缘信息丰富的图像上取得较精确的分割结果。然而，二维Otsu 法本身仅局限于分割目标和背景呈正态分布且方差相当的图像，因此这些基于二维Otsu 法改进的方法仍然难以分割具有无峰或单峰直方图模式的图像。Yang 等［15］提出基于灰度和局部相对熵的二维阈值分割方法，不仅考虑了非对角区域的边缘像素，而且通过最小相对熵进一步提高了方法的鲁棒性。该方法虽然在无峰、双峰直方图模式的灰度图像上能获得较好的分割结果，但其时间复杂度高达O(L4)。

大多数二维阈值分割方法将二维直方图视为两个或多个不同区域之间的一种特征映射，然后在二维直方图上构造目标函数以计算分割阈值。直方图虽然计算简单，但存在数据离散和形态多变等缺点，这也是基于直方图的阈值分割方法无法分割不同直方图模式的根本原因［11-15］。生存函数是一种与直方图截然不同的特征映射新方法，具有良好的平滑性和单调非递增性。累积剩余Tsallis 熵（Cumulative Residual Tsallis Entropy，CRTE）是一种基于生存函数的信息测度［16］，生存函数所具有的优良性质使得CRTE 在离散或连续领域都有一致的定义，为分割具有不同直方图模式的图像奠定了理论基础。为了克服现有二维阈值法在分割精度和计算效率方面的不足，同时为了在同一个框架内分割具有不同直方图模式的图像，本文提出了一种快速二维累积剩余Tsallis 熵阈值分割方法（Fast 2D-CRTE）。该方法从图像二维灰度直方图构建二维生存函数出发，通过最大化二维生存函数不同区域之间的2D-CRTE 计算分割阈值。同时，为了降低方法的时间复杂度，通过递推计算将方法的时间复杂度降为O(L2)。

2 Fast 2D-CRTE 方法

本节首先基于二维直方图构建出二维生存函数，然后再在二维生存函数的基础上定义计算分割阈值的二维累积剩余Tsallis 熵目标函数。为了将目标函数求解的时间复杂度降低到O(L2)，进一步给出目标函数的快速递推计算方法。

2.1 二维生存函数

给定一幅大小为M×N的图像I(x，y)，在图像I(x，y)上运用3×3 的均值滤波得到均值图像G(x，y)如式（1）所示：

二维直方图具有数据离散和形态多变的特点，这使得目前大部分基于二维直方图的阈值方法难以在同一个阈值选择目标函数内分割不同直方图模式的图像。二维生存函数是一种新的特征映射方法，可以通过二维直方图推导得到式（3）：

其中：0 ≤s≤L-1，0 ≤t≤L-1。与二维直方图多样且复杂的形态相比，二维生存函数拥有更统一的分布形态。图1 展示了不同二维直方图模式所对应的二维生存函数。可以观察到，不管是无峰、单峰、双峰或者多峰模式的二维直方图，其对应的二维生存函数曲面都呈现单调非递增的形态。这为在同一阈值选择目标函数下分割具有不同直方图模式的图像奠定了理论基础。

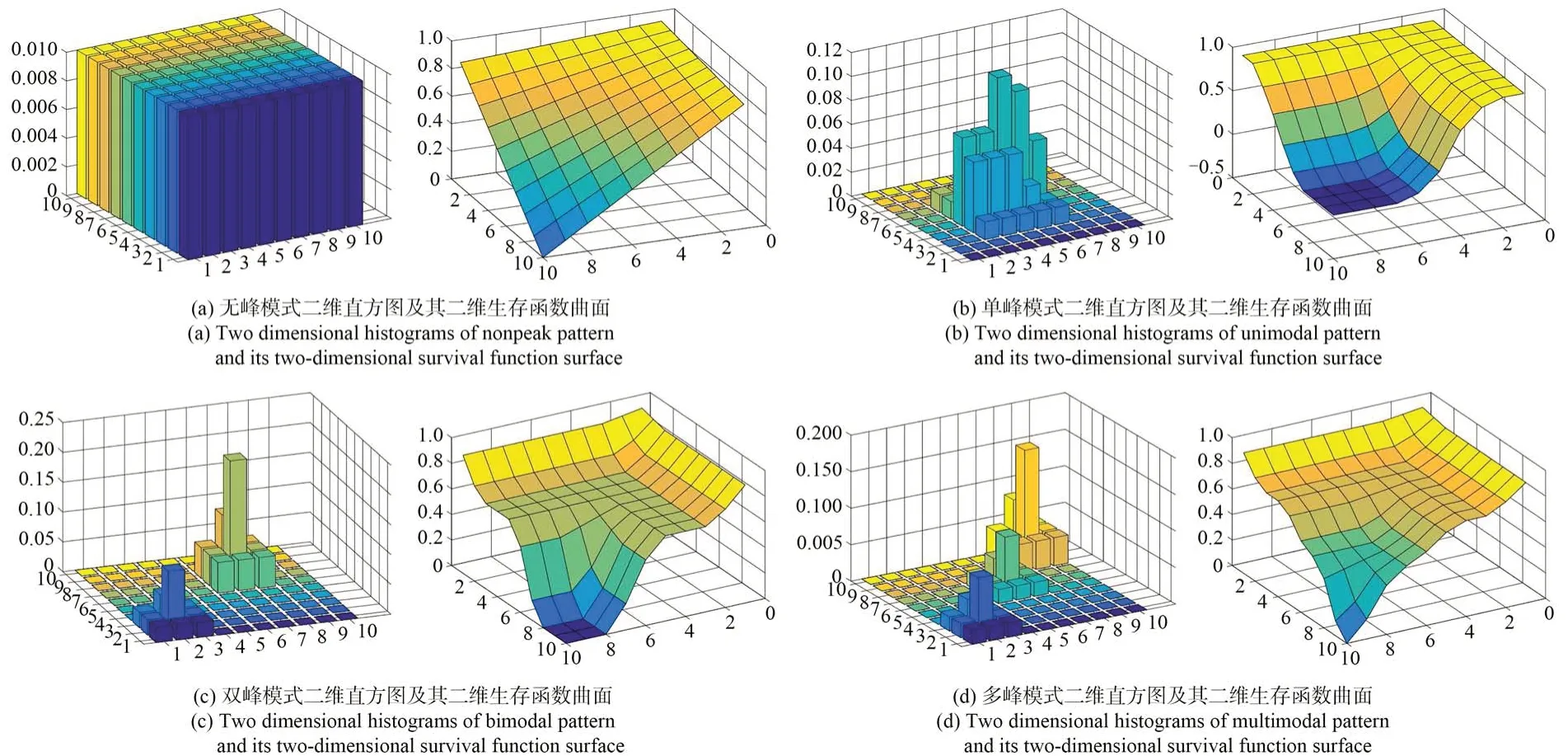
图1 不同模式二维直方图及其对应二维生存函数曲面Fig.1 Two-dimensional histograms of different modes and their corresponding two-dimensional survival function surfaces

2.2 二维累积剩余Tsallis 熵目标函数

CRTE［16］是一种基于生存函数Fˉ(x)的信息测度，定义如式（4）所示：

假设阈值向量(s，t)将图像对应的二维生存函数划分为如图2 所示的4 个矩形区域。与二维直方图区域划分类似，二维生存函数中区域A 与目标对应，区域B 与背景对应，区域C 和D 则表示边缘和噪声。

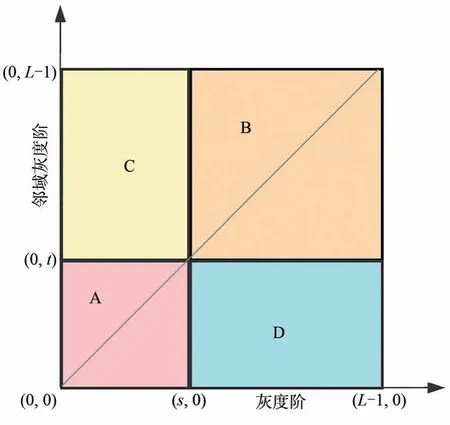
图2 二维生存函数区域划分Fig.2 Two-dimensional survival function region division

根据式（5）的2D-CRTE 定义，目标和背景对应区域A 和B 的2D-CRTE 可以分别按式（6）和式（7）计算：

因为区域C 和D 通常对应边缘和噪声，对于最终分割阈值的选取影响不大而被忽略，这样根据两个不同子系统的2D-CRTE 可加性原则，总的2D-CRTE 定义如式（8）所示：

最后，构建计算分割阈值向量(s*，t*)的目标函数：

2.3 目标函数的快速计算

在二分类的情况下，确定阈值向量(s*，t*)的计算复杂度高达O(L4)。为了提高2D-CRTE 阈值分割方法的计算效率，提出一种时间复杂度为O(L2)的递推算法。

在公式（8）中，为了计算阈值向量(s*，t*)，在0～（L-1）的穷举是不可避免的，其本身的时间复杂度已经为O(L2)。因此，降低算法总体时间复杂度须从公式（6）和公式（7）着手，采取空间换时间的方法，提前计算出不同阈值向量(s，t)下目标区域和背景区域的2D-CRTE。

图3 展示了Fast 2D-CRTE 方法快速计算不同阈值向量(s，t)下 总2D-CRTE 的思路，其中R(s，t)和B(s，t)分别表示目标区域和背景区域对应的2D-CRTE 的信息量：

图3 Fast 2D-CRTE 方法计算不同阈值向量(s，t)下总2D-CRTE 的思路。Fig.3 Fast 2D-CRTE method for calculating total 2D-CRTE with different threshold vectors (s，t).

将式（10）和式（11）分别代入式（6）和式（7），则式（8）可以转换为：

这样，计算总的2D-CRTE 就退化为计算辅助计算量R(s，t)和B(s，t)。进一步，R(s，t)可以通过如式（13）所示的快速递推公式得出：

R(s，t)初始值可按式（14）初始化：

在二维生存函数的基础上，可以在O(L2)的时间复杂度内得到R(s，t)。B(s，t)的计算还需要一个额外的辅助空间T(s，t)，T(s，t)表示包含坐标(s，t)在内的左上角区域信息量的总和（见图4 长方形内最右侧红色区域）。T(s，t)的计算与R(s，t)类似，可以通过如式（15）所示的快速递推公式得出：

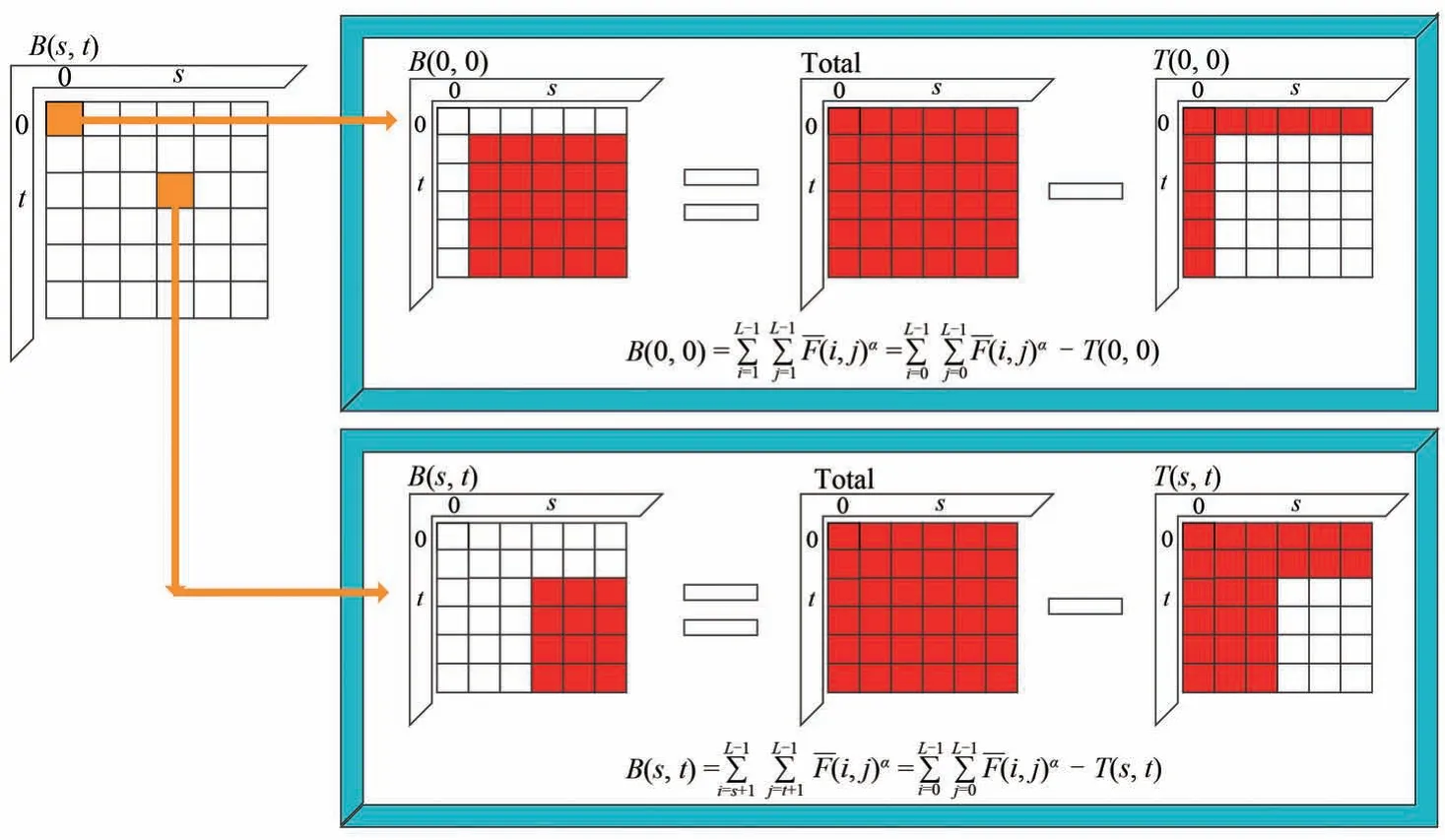
图4 辅助计算量B(s，t)计算思路（B(s，t)等于总的信息量减去在阈值向量(s，t)下对应的T(s，t)）。Fig.4 Calculation thought of auxiliary amount B(s，t)（B(s，t) equals the total amount of information minus the corresponding T(s，t) under the threshold vector (s，t)）.

T(s，t)初始值可按式（16）初始化：

在得到辅助计算量T(s，t)后，B(s，t)可以通过总信息量减去T(s，t)得到，图4 形象地描述了B(s，t)和T(s，t)的关系，计算公式如式（17）所示：

从上述分析推理可知：Fast 2D-CRTE 一共使用了3 个辅助空间R(s，t)、B(s，t)和T(s，t)，空间使用量为3×(L×L)，然而其时间复杂度仅为O(L2)，优于原始2D-CRTE 的O(L4)。

3 算法描述

为了更清晰地说明如何利用式（1）～式（3）、式（9）和式（12）～式（17）计算阈值向量(s*，t*)，给出了快速二维累积剩余Tsallis 熵阈值分割方法（Fast Two-Dimensional Cumulative Residual Tsallis Entropy，Fast 2D-CRTE）的6个步骤，如图5和算法1所示。

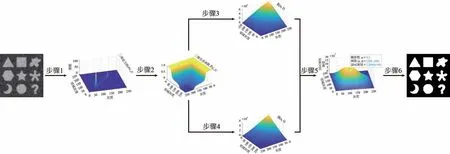
图5 提出的Fast 2D-CRTE 方法的流程Fig.5 Flow chart of the proposed fast 2D-CRTE method

4 实验结果与分析

4.1 实验方案及量化指标

实验所用软硬件的主要参数如下：Intel（R）Core（TM）i5-10300H 2.50 GHz CPU，16 GB DDR4内存，Windows10 64 位操作系统，Matlab 2021 开发平台。测试图像集包括26幅合成图像和76幅真实世界图像，它们的灰度直方图呈现为无峰、单峰、双峰或者多峰模式。每幅测试图像的分割参考图像均利用Adobe Photoshop 软件手工产生。测试图像集和分割参考图像集可以通过访问https：//pan.baidu.com/s/16HVrqsNSM83uPmai-6idVQ？pwd=7rfx 获得。

为了评估所提出方法的计算效率以及针对不同直方图模式图像的分割有效性，在测试数据集上比较了6 种不同的图像分割方法，分别是本文提出的Fast 2D-CRTE、快速二维Otsu 阈值分割方法（Fast Two-Dimensional Otsu，Fast 2D-OTSU）［11］、快速二 维Tsallis 阈值分 割方法（Fast Two-Dimensional Tsallis，Fast 2D-Tsallis）［12］、基于超像素的快速模糊C 均值聚类分割方法（Superpixel Based Fast Fuzzy C-Means Clustering，SFFCM）［17］、自动模糊聚类分割方法（Automatic Fuzzy Clusering Framework，AFCF）［18］、基于模糊区域的活动轮廓图像分割方法（Gobal and Local Fuzzy Image Fitting Image Segmentation，GLFIF）［19］。

本文采用常用的量化指标，即误分类率（ME）［15］来定量评估分割方法的分割精度。ME 指标反映了分割结果图像中背景像素和前景像素误分类的情况。当分割结果图像和分割参考图像相同时，ME=0；反之，当分割结果图像和分割参考图像完全相反时，ME=1。ME 计算公式如式（18）所示：

其中：Fg和Bg分别表示分割参考图像中的前景和背景，而Ft和Bt分别表示分割结果图像的前景和背景，符号∩表示取交集运算，符号|· |表示计算元素的个数。

4.2 合成图像上的比较实验

为了验证Fast 2D-CRTE 方法的分割适应性，一方面通过调整目标和背景的大小比例，使得26 幅合成图像既包括目标和背景大小比例相对均衡的情况（图6（a）、（c）和（d）），也包括大小比例相对失衡的情况（图6（b））；另一方面在合成图像上添加诸如均匀噪声、高斯噪声、贝塔噪声和瑞利噪声，以形成具有无峰、单峰、双峰或者多峰直方图模式的合成图像（图6（a）～（d））。

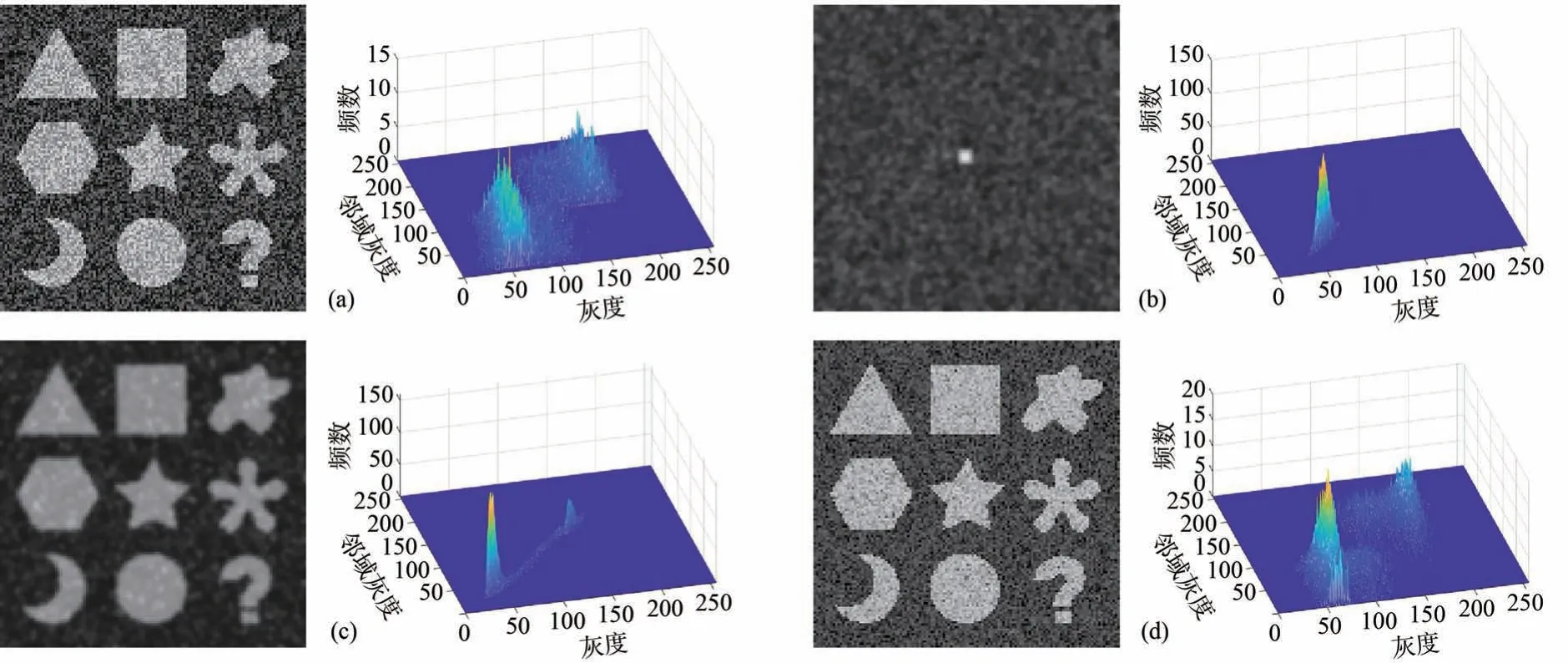
图6 4 张合成测试图像及其二维直方图（（a）～（d）分别对应编号为1、4、18 和26 的测试图像）。Fig.6 4 synthetic test images and their two-dimensional histograms（（a）～（d）corresponding to test images numbered 1，4，18，and 26，respectively）.

图7 展示了6 种分割方法在4 幅合成图像上的分割结果。表1 第1、4、18 和26 行分别给出了6 种分割方法在4 幅合成图像上的ME 值。结合二者可以观察到：（1）AFCF 方法除了在双峰直方图模式的图像上分割效果较好之外，在无峰、单峰或多峰直方图模式的图像上都有严重的误分割，ME 值甚至高达0.67。（2）Fast 2D-OTSU方 法、Fast 2D-Tsallis 方 法、SFFCM 方法和GLFIF 方法的整体分割效果优于AFCF 方法，在无峰和双峰直方图模式图像上的分割效果有很大提升。然而，这些方法对单峰直方图模式图像仍然具有较差的分割能力，ME 值达到0.4（表1 第4 行）。（3）Fast 2D-CRTE 方法的 分割结果明显优于前5 种方法，不仅成功地将目标从图像中提取出来，而且分割结果最接近GroundTruth图像。

表1 6 种分割方法在26 张合成图像上的ME 值以及Fast 2D-CRTE 方法的熵参数α 取值和分割阈值Tab.1 ME value of 26 synthetic images by six segment methods and entropy parameter α values and segmentation thresholds of Fast 2D-CRTE method

图7 6 个方法在图6（a）～（d）中4 幅合成图像上的分割结果Fig.7 Segmentation results of 6 methods on 4 synthetic images in Fig.6（a）～（d）

表1 给出了6 种分割方法在26 张合成图像上具体的ME 值以及Fast 2D-CRTE 方法在26 张合成图像上熵参数α的取值和分割阈值。表2 给出了6 种分割方法在26 幅合成图像上的平均CPU运行时间和平均ME 值。结合表1 和表2 可以得到：（1）Fast 2D-CRTE 方法在无峰、单峰、双峰或多峰直方图模式图像上保持了良好的稳定性，平均ME 值 为0.011 9。（2）Fast 2D-CRTE 方法较性能第二的Fast 2D-OTSU 方法，平均ME 值降低6.25%，平均CPU 运行时间降低0.01 s，在ME 值和时间效率方面具有相对明显的优势。

表2 6 种分割方法在26 张合成图像上的平均CPU 运行时间以及平均ME 值Tab.2 Average CPU runtime and mean ME value of 26 synthetic images by six segment methods

4.3 真实图像的比较实验

具有不同灰度直方图模式的76幅真实世界图像被用于进一步检验6 种分割方法的分割适应能力，如图8 所示。这些真实世界图像的灰度直方图可以用一种或多种分布的组合来近似，且直方图呈现无峰、单峰、双峰或多峰模式。这76 幅测试图像被分为4 组，其中编号1～5、6～26、27～53 和54～76 的测试图像直方图分别对应无峰、单峰、双峰和多峰模式。测试图像采集自不同应用领域，包括生物细胞分析、行人视频监控和舰船目标监测等，涉及的成像方法包括超声成像、红外热成像、涡流成像、光学显微镜成像和光学CCD 成像等。

图9 展示了Fast 2D-CRTE 方法在图8 的4 幅真实世界图像上的仿真过程，图10展示了6种分割方法在图8中4幅真实世界图像上的分割结果。结合二者可以观察到：（1）AFCF 方法整体的分割适应性较低，在灰度直方图为无峰、单峰、双峰或多峰模式的图像上具有严重的误分割。（2）SFFCM方法和GLFIF 方法针对双峰直方图模式的图像具有较好的分割精度。然而，它们在单峰和多峰直方图模式图像上的分割仍然不理想。（3）相比于前3 种方法，Fast 2D-OTSU 方法和Fast 2D-Tsallis方法的分割效果有很大提升，但是它们在无峰、单峰和多峰直方图模式图像上仍然存在误分割。（4）从仿真实验结果可以看出，通过合理地调整熵参数，Fast 2D-CRTE 方法能选取恰当的分割阈值从复杂的场景下将目标提取成功，在不同直方图模式图像上具有较强的分割适应性。

图9 在图8 中4 幅真实世界图像上的二维生存函数、R(s，t)、B(s，t)和2D-CRTE 的可视化结果。Fig.9 Visualization results of two-dimensional survival function，R(s，t)，B(s，t) and 2D-CRTE on 4 real-world images in Fig.8.

图10 6 种分割方法在图8 的4 幅二维直方图模式分别为无峰、单峰、双峰和多峰图像上的分割结果。Fig.10 Segmentation results of 6 methods on 4 histogram patterns of Fig.8 are nonpeak，unimodal，bimodal and multimodal.

图11 展示了6 种分割方法在76 张真实世界图像上的ME 值散点图，表3 则给出6 种分割方法的平均CPU 运行时间和平均ME 值。结合二者可得：（1）SFFCM 方法、AFCF 方法和GLFIF方法在无峰、单峰、双峰或多峰直方图模式图像上的ME 值波动较大（见图11 散点图（d）、（e）和（f）），对应平均ME 值分别高达0.499 4、0.540 7和0.366 8，进一步说明这3 种方法的分割稳定性较差。（2）Fast 2D-OTSU 方 法和Fast 2D-Tsallis方法相较于前3 种方法，在双峰直方图模式图像上的分割精度较高（见图11（b）和（c）的实心圆形标识的数据）。但是，Fast 2D-OTSU 方法和Fast 2D-Tsallis 方法在无峰、单峰或多峰直方图模式的图像上的分割结果也不稳定。（3）针对无峰、单峰、双峰或多峰直方图模式的图像，Fast 2D-CRTE方法的ME 值波动平缓（图11（a））且平均ME 值稳定在0.013 7。这些都表明，Fast 2D-CRTE 方法具有更强的分割适应能力。此外，相对于其他5 种方法，Fast 2D-CRTE 方法的平均CPU 运 行时间稳定在0.183 2 s，位居第一。

表3 6 种分割方法在76 张真实世界图像上的平均CPU 运行时间以及平均ME 值Tab.3 Average CPU runtime and mean ME value of 6 segmentation methods on 76 real-world image

图11 6 种分割方法在76 张真实世界图像上的ME 值散点图Fig.11 ME value scatter maps of 6 segmentation methods on 76 real-world images

4.4 熵参数α 选取分析

在本文提出的方法中，存在一个可变的熵参数α，该值的改变影响着最佳阈值的选取。式（8）描述了随着阈值变量(s，t)的变化时，两个子系统（A，B 区域）总的2D-CRTE 熵值的变化。从中可以看出，2D-CRTE 熵值的大小与阈值向量(s，t)划分A、B 区域后的二维生存函数Fˉ和熵参数α相关。在图像给定的情形下，二维生存函数Fˉ本身并不发生改变，导致总的2D-CRTE 熵值改变的原因来自于熵参数α的变化影响下的式（6）和式（7）的分子项和的改变。

图12 第一、二行子图分别给出了在一幅最大灰度为50 的图像上取熵参数α为0.001、0.1、0.5、0.99、1.1 和1.5 时的二 维生存 函数Fˉα和总的2D-CRTE 熵变化。并且，图中颜色越接近于黄色代表数值越接近最大值，图中颜色越接近蓝色代表数值越接近于最小值。为了便于描述，称图中最大值和最小值之间的区域为缓冲区。从第一行子图可以看出，熵参数α越接近于0，缓冲区中的所有取值就越趋近于1（颜色趋近于黄色）；熵参数α越远离（大于）0，缓冲区中其余取值都趋近于0（颜色趋近于蓝色）。该现象表明，可以通过动态调整熵参数α改变二维生存函数缓冲区内部的数值，进而影响最佳阈值的选取。从图12 的第二行子图可以看出，当熵参数0<α<1 时，随着α的减小，2D-CRTE 熵值的选取会向二维直方图的中心点移动；当熵参数α>1 时，随着熵参数α的增大，2D-CRTE 熵值可以在中心点右侧多个局部区域取得。因此，熵参数α>1 时的图像分割结果并不唯一。

图12 熵参数α 取0.001、0.1、0.5、0.99、1.1 和1.5 时的生存函数和总的2D-CRTE 熵变化。Fig.12 Survival function and total 2D-CRTE entropy change for entropy parameter α at 0.001，0.1，0.5，0.99，1.1 and 1.5.

综上分析，熵参数可以在分割过程中起到调解因子的作用。Fast 2D-CRTE 阈值分割方法可以通过调整熵参数α改变二维生存函数以适应不同的图像分割任务。通过4.2 和4.3 节中的大量实验发现，（0，1.1）是选取熵参数α的适宜区间。参数在选取0.001、0.01、0.1、0.5、0.99 和1.1 等数值时，一般会取得一个不错的分割结果。

对于具体的图像分割任务，任务场景与成像条件在一定时间和空间范围内是可控的。因此，在对图像进行处理时，可以假定来自相同背景和相同成像设备的一系列图像的熵参数α是一致的。对于相同的应用场景，可以通过一些训练样本图像从0.001、0.01、0.1、0.5、0.99 和1.1 等6 个备选熵参数中为熵参数α选择一个最优值，然后将所选的最优值设置为该场景下一系列图像分割的熵参数α。为了证实这一想法的可行性，我们从MSTAR 数据库［20］中选取10 幅同一场景下的雷达测试图像展开实验，雷达测试图像及其二维直方图如图13 所示。

图13 10 幅雷达测试图像及其二维直方图（从左到右，从上到下依次编号为1～10）。Fig.13 10 Radar test images and their two-dimensional histograms（number 1～10 from left to right，top to bottom）.

由于任务场景与成像条件相似，10 幅雷达测试图像的二维直方图呈现一致的单峰模式（图13）。图14 展示了在选定熵参数α=0.001时Fast 2D-CRTE 方法针对图13 中编号为1 和6的雷达测试图像的仿真过程；图15 给出了在选定熵参数α=0.001 时Fast 2D-CRTE 方法在图13中10 幅雷达测试图像上的分割结果。结合二者可得：对于这10 幅同一场景下的雷达测试图像，当熵参数α取0.001 时，Fast 2D-CRTE 方法能消除单峰模式下背景像素簇对阈值的权重偏离影响，进而选取合理的阈值成功地将目标从图像中提取出来。该实验也验证了前面的假设。在本文实验中，所有2D-CRTE 的熵参数α都是手动从0.001、0.01、0.1、0.5、0.99 和1.1 等6 个备选熵参数选取的，如何自适应地选取合适的熵参数α也是后续研究需要考虑的问题。

图14 在图13 中编号为1 和6 的测试图像上的二维生存函数、R(s，t)、B(s，t)和2D-CRTE 的可视化结果。Fig.14 Visualization results of two-dimensional survival function，R(s，t)，B(s，t) and 2D-CRTE on test images numbered 1 and 6 in Fig.13.

图15 Fast 2D-CRTE 方法在图13 的10 幅雷达测试图像上的分割结果Fig.15 Segmentation results of Fast 2D-CRTE method on 10 radar test images

5 结 论

本文给出的二维累积剩余Tsallis 熵可以表征分割前后图像之间的差异程度，具备图像分割测度功能。基于二维生存函数的快速二维累积剩余Tsallis 熵阈值分割方法通过动态地调整熵参数，能有效地区分无峰、单峰、双峰或多峰直方图模式图像的目标和背景。实验结果表明，与快速二维Otsu 法、快速二 维Tsallis 熵法、2 种聚类分割方法和1 种活动轮廓分割方法相比，所提出的方法不仅时间效率以0.183 2 s 位居第一，而且平均误分类率保持在0.013 7 以下，在不同直方图模式的图像上具有较强的分割鲁棒性。在未来工作中，将会考虑构建累积剩余Tsallis 熵参数和不同直方图模式之间的关系，实现自适应地解决参数调节问题。