基于改进U-Net 网络的图像混合畸变校正方法
宋 巍,师丽彪,耿立佳,马振玲*,杜艳玲
(1.上海海洋大学 信息学院,上海 201306;2.国家海洋局 东海标准计量中心,上海 201306)
1 引 言
广角镜头由于其宽阔的视野,被广泛应用于各种计算机视觉任务中,包括深度估计[1]、视频监控[2]、物体检测与识别[3]等。然而广角镜头大多数存在镜头畸变,影响目标测量与特征提取精度。因此,图像几何畸变校正是许多计算机视觉应用的关键预处理步骤。
相机标定法[4-6]是最常用的图像畸变校正方法,该方法可以借助特定的标定板来求解相机的内参数、外参数和畸变参数,也可以基于图像的几何特征建立约束条件进行求解。Sun 等人[7]提出了基于两条正交平行线消失点优化的校正方法。Workman 等人[8]估计了单幅图像中的地平线。文献[9]利用双正交消失点优化方法结合直线在畸变校正后也应为直线的特性来完成相机标定工作。这类方法需要事先已知相机镜头畸变类型,并能用数学模型进行描述,然而现在传感器类型众多,成像环境复杂,图像畸变类型复杂,很难用固定的数学模型对畸变进行描述,因此该校正方法的适用性受到限制。
随着深度学习技术在计算机视觉方向的快速发展,该技术也逐渐被学者应用到图像的几何畸变校正工作上。早期使用卷积神经网络(Convolutional Neural Networks,CNN)进行径向畸变校正的相关工作是2016年由Rong等人[10]提出的。该方法基于单参数模型[11],将一个固定范围的畸变参数离散为400 种类别,并以此为基础生成训练数据集,将畸变校正任务转变为畸变参数分类任务。文献[12]也是基于畸变参数分类的思想,使用具有自校准运动恢复结构(Structure From Motion,SFM)重建图像序列来获得相机的畸变参数和二者的函数关系来简化畸变模型,利用CNN 网络提取径向畸变的特征,最后将两个畸变参数预测问题转为单个参数的分类问题。2019 年,Liao 等人[13]提出了一个畸变校正生成对抗网络,这是首个采用端到端对抗网络来学习两幅图像之间的结构差异然后进行畸变校正的方法,该方法与Rong 等人方法[10]对比实现了无标签训练。2019 年,Li[14]提 出了一种校正框架实现盲几何畸变校正,同时提供了一种几何畸变数据集的构建方法。该方法中使用CNN 来学习校正图像和畸变图像之间像素坐标位移的变化,将图像的校正工作转为像素坐标位移变化的预测。2020 年,文献[15]基于单参数模型提出了一种新的模型,构建了径向畸变合成层和校正层(Radial Distortion Synthesis and Correction layers,RDS&RDC),该方法数据的合成和校正速度得到了提升。2021 年,文献[16]设计了一个多层次的校正流程,将校正任务分解为结构恢复、语义嵌入和纹理渲染3 个层次,使用分层结构实现渐进式校正图像并取得了较好的结果。文献[17]提出了一种将图像校正问题映射为从图像中学习序数畸变的方法,序数畸变表示了图像中像素的畸变程度,它从图像中心点向外依次增加。目前基于深度学习的图像几何畸变校正方法大多针对单一畸变类型,而相机获取的影像包含径向畸变、切向畸变等多种混合畸变,因此当前方法在解决混合畸变校正时存在明显局限性。
针对传统校正方法依赖畸变数学模型适用性较差和深度学习方法在校正混合畸变存在局限性的问题,本文提出了一种结合空间注意力机制与U-Net 网络来校正混合畸变的方法。本文综合考虑图像径向和切向混合畸变构建了畸变图像数据集,使用畸变图像和无畸变图像之间的像素坐标位移变化来表示畸变,将校正问题转为预测畸变图像的逐像素坐标位移变化。利用U-Net 编解码器结构网络来学习畸变图像的多尺度特征及重建畸变图像坐标位移图,同时引入空间注意力机制来响应畸变图像中不同位置畸变程度的影响,设计了坐标差损失和图像重采样损失两种损失函数来提高校正精度。与最新基于深度学习的畸变校正方法的对比实验表明,本方法的校正效果最优,图像校正坐标向量的平均绝对误差约为0.251 9,主观评价的评分为4.597。
2 数据集构建
2.1 混合畸变模型
摄像机成像的基本原理是针孔相机模型,但是由于相机的制造精度和组装工艺等的偏差会引入畸变,导致图像的成像模型不满足针孔相机模型,因此需要考虑成像几何畸变问题。大多数透镜的畸变主要由径向畸变和切向畸变构成[18]。径向畸变是图像像素点以畸变中心为中心点,沿着径向产生的位置偏差;切向畸变由透镜本身与相机传感器平面不平行引起。在物理坐标系下,实际像点p(x,y)与理想无畸变像点的数学关系表述为:
式中:r2=x2+y2,k1、k2、k3是径向畸变系数,p1、p2是切向畸变系数。径向畸变与切向畸变为r的多项式表达式,根据林德曼-魏尔斯特拉斯定理,任何函数(混合畸变)都可以由多项式拟合得到[19],因此,本文选择径向畸变和切向畸变的多项式数学表达式来描述混合畸变。
2.2 图像数据集选择
为了训练本文网络来完成几何畸变校正工作,需要准备大量的数据集作为预备数据集。目前基于深度学习的方法对畸变图像校正的研究工作中,数据集都是单一的径向畸变而且畸变图像的分辨率较小,多为256 pixel×256 pixel,会损失掉畸变程度较大的图像边缘信息。考虑到包含径向畸变的图像,其畸变距离图像中心越远畸变程度越大,因此为了保留较多的畸变特征需要生成较大分辨率的畸变图像。
首先需要选择图像数据源。基于上述考虑,本文选择了place365 图像数据集[20],并将数据集中的图像裁剪为512 pixel×512 pixel 的大小。对于具有明显的几何结构的图像,如直线、弧线、地平线等,可以提供大量的几何信息供网络学习,因此我们进一步对此类图像进行了筛选,利用霍夫变换筛选出来具有明显直线结构的图像,筛选条件定义为:
式中:C为图像的分辨率大小,l表示检测的直线长度,α为最短直线段的长度。本文中指定α=80,约为图像分辨率的1/6;λ为数据集的选择因子,该值由源数据集图像数量和需求数据集图像数量来确定,值越大筛选的图像直线越多,相应地筛选出的图像数量越少,最终选择λ=4 筛选了1 800 张图像作为数据集。
其次,基于传统相机标定的思想,棋盘格图像可以为图像几何畸变校正提供最显著的几何特征,因此本文通过设定不同的方格大小和图像的旋转角度来多样化棋盘格的特征,生成1 800 张棋盘格图像(512 pixel×512 pixel)扩充数据集。
2.3 数据集生成
不同于Li[14]基于单参数畸变模型的径向畸变数据集构建方法,本文提供了一种混合畸变类型的数据集构建方法。由公式(1)可知,本文使用的畸变模型包含两种畸变类型,该模型对于径向畸变的描述由多个畸变参数k来确定,而且还可以通过添加切向分量来扩展以处理非径向对称的畸变,而单参数模型仅只能描述径向对称的畸变。数据集的具体构建流程如下:
首先,对GoPro 相机的不同模式进行相机标定工作,获取4 种不同的相机内参数fx、fy、cx、cy和畸变参数k1、k2、k3、p1、p2,详细参数如表1 所示。然后,依据公式(1)中坐标的映射关系生成混合畸变图像(512 pixel×512 pixel)数据集I和其对应的坐标差数据集V,坐标差数据集V记录了在像素坐标系下畸变图像中的像素点p(x,y)与其相对应的无畸变的图像中的像素点的差值。由于生成的畸变图像在边缘存在黑边,且考虑尽量保留远离图像中心的信息,因此在图像中心裁剪出352 pixel×352 pixel 大小的图像和坐标差向量作为最终的数据集,最终生成畸变图像14 400 张,其中12 000 张用于训练模型,2 400 张用于测试模型。合成数据集的部分图像如图1 所示。

图1 合成数据集的部分图像Fig.1 Part of the images in the synthetic dataset

表1 相机内参数与畸变参数Tab.1 Camera inner parameters and distortion parameters
3 实验方法
本文设计的畸变校正网络架构如图2 所示。图中(a)为输入畸变图像,(b)是U-net 主干网络,(c1)是模型预测的坐标差矩阵,(c2)是坐标差矩阵的标签,(d1)是模型校正后的图像,(d2)是图像的标签。本文使用U-Net[21]作为主干网络模型来提取图像的特征,并让网络学习从畸变图像域到校正坐标域的映射。校正坐标域与输入的畸变图像具有相同大小的二维向量,通过预测的校正坐标域向量进行图像重采样来获得校正后的图像。校正坐标域的预测值和校正图像的精度相关,因此本文重点设计了损失函数来提高模型的预测精度。

图2 网络架构Fig.2 Network architecture
3.1 U-Net 主干网络
U-Net[21]网络最初由Ronneberger 在2015 年发表,应用在医学图像分割领域中并取得了良好的分割效果。该网络基于Encoder-Decoder 结构,是一种U 形对称结构,主要结构包括下采样、上采样和跳跃连接。在网络的下采样部分,对图像进行编码,由尺寸为3×3 的卷积层、ReLU 函数和尺寸为2×2 的池化层构成,对输入的图像进行4 次下采样操作,每次下采样操作后特征图的尺寸下降,同时通道数翻倍。在网络的上采样部分,对图像进行解码,通过4 次尺寸为2×2 的反卷积层实现上采样,扩大特征图尺寸,恢复到输入图像尺寸大小。网络的跳跃连接结构将解码层中的高层特征和编码层中的低层特征进行融合、抽象特征与细节特征进行融合,实现了多尺度特征融合,使得捕获的特征图既包含全局信息,又包含局部信息,提高了特征的表现力。
选择U-Net 网络可以更好地提取畸变图像的特征,且模型的训练速度也得到了提升。将一张三通道的畸变图像输入到网络,经过模型的学习输出一个具有和输入图像相同尺寸大小的二维坐标差向量。
3.2 空间注意力机制
在畸变图像中,畸变程度由中心向图像四周逐渐扩大,因此本文在编码器网络输出层加入了空间注意力机制(Spatial Attention,SA)[22],既保证了主干网络充分提取图像的特征,又从空间维度细化了提取到的特征图。空间注意力模块如图3 所示,将输入的特征图在每一个特征点的通道上取最大值和平均值,将结果堆叠,再通过一个卷积核为7×7 大小的卷积层得到通道数为1 的特征图,然后将该特征图通过sigmoid 函数后与输入特征图相乘得到输出特征图。其具体计算公式如式(3)所示:
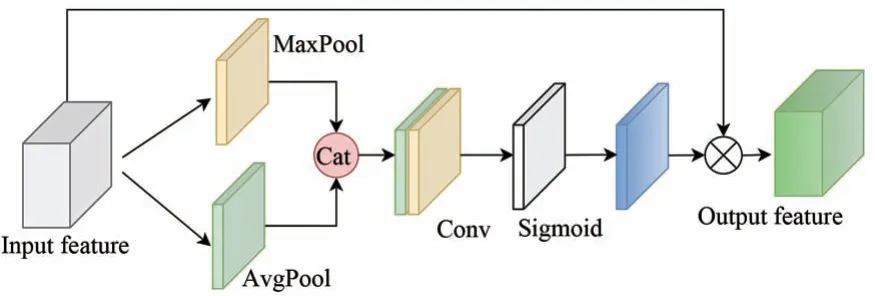
图3 空间注意力模块结构Fig.3 Structure of the spatial attention module
式中:I代表输入特征图,O代表输出特征图,f7(· )表示卷积核为7×7 的卷积运算,cat 表示堆叠操作,δ是Sigmoid 函数。
3.3 坐标差损失
在Li[14]的方法中,损失函数(Endpoint Error,EPE)表示为预测的坐标差向量与真值之间的欧氏距离,网络估计的坐标差向量Vpred是对畸变图像的逐个像素进行预测,表示了畸变图像的像素应该如何移动到原始无畸变图像中对应的像素。本文首先使用平均绝对误差(Mean Absolute Error,MAE)作为损失函数,表示预测的坐标差向量Vpred与真值Vgt之间的平均绝对误差,其定义为:
式中,n为坐标差向量元素总数。
经过对预测坐标差向量分析,发现预测向量呈现出偏离中心越远预测误差越大的特征,因此我们设计了权重向量M来优化上述损失函数,使得网络能够提高对坐标差向量边缘的预测精度。以坐标差向量对应的真值向量Vpred的逐像素点到坐标(0,0)的欧氏距离作为权重指标,将欧式距离归一化后得到权重向量M,M具有和预测坐标差向量Vpred相同的形状,其定义由公式(5)给出:
式中,G是归一化函数。
最终,坐标差损失函数定义为:
式中:n为坐标差向量元素总数,M为权重向量。
3.4 重采样损失
最终的校正图像由预测的坐标差向量对畸变图像进行重采样得到。为了进一步提高校正效果,本文设计了一个图像重采样损失函数L2,表示由预测坐标差向量重采样后得到的校正图像Ipred与无畸变图像Igt之间的逐像素点的欧式距离。将其定义为:
式中,n表示像素点的个数。
最终本文的损失函数定义为:
其中:权重μ在坐标差预测和重采样损失之间提供了权衡,本文中μ=0.5。
4 实验结果与分析
4.1 实验环境与参数设置
本文实验在Tesla-P100 GPU 上进行,选用Pytorch 深度学习框架进行算法实现,运行环境为Python3.6、Pytorch1.8、cuda10.1。批尺寸(Batch size)的值为24,优化器使用Adam(Adaptive Moment Estimation),学习率设定为1×10-4,共迭代200 epoch 后收敛。
4.2 评价指标
本文采用3 个评价指标。第一个指标定义为网络预测的坐标差向量Vpred与真值Vgt之间的平均绝对误差,该指标直接反应了模型的预测精度。该值越接近于0 表明网络预测的坐标差向量精度越高,相应地重采样生成的图像校正效果越好。其他两个指标沿用了图像校正研究常用的评价指标[23-24],这两种指标反应了校正后图像的质量以及校正精度;峰值信噪比(Peak Signal to Noise Ratio,PSNR)和结构相似性指数(Structural Similarity,SSIM)。PSNR 值高于20 dB 图像质量才能被接受,该值越大,表明图像失真越少。SSIM值的范围为0~1,值越大代表校正后的图像质量越接近原图。
4.3 与其他方法的对比
为了验证本文方法的有效性,对比了两种最新基于深 度学习 的Li[14]和Hosono[25]的几何 畸变图像校正方法以及3 种采用不同主干网络U-Net[20]、PSPNet[26]、DeepLabV3+[27]的模型。
虽然近年来有多种基于深度学习的几何畸变图像校正方法被陆续提出,但由于没有公开代码不便进行对比。因此,本文选择了有公开代码的Li[14](2019 年)和Hosono[23](2021 年)的方法,并使用本文构建的数据集对其进行了训练和测试。Li提出的盲目校正多类型几何畸变的方法采用了编解码网络来学习畸变图像的特征,以预测的坐标差向量与真值之间的欧氏距离作为损失函数,通过预测的坐标差向量来重采样畸变图像实现校正。Hosono 的方法以VGG 网络为基础构建了畸变参数评估网络模型来预测畸变图像的畸变参数进而实现校正,利用扭曲的直线校正后仍为直线的特性提出了线条重构误差损失来提高网络的预测精度。这两种方法有一定的代表性。
此外,考虑到主干网络结构对性能的影响,在本文输入、输出及损失函数不变的前提下,替换主干网络后进行训练和测试。对比的主干网络包括在细粒度特征学习方面表现优秀的PSPNet、DeepLabV3+网络以及本文选择的基础网络UNet。PSPNet 通过整合全局上下文信息的金字塔池化模块增强了多尺度信息的融合,减小了局部和全局的损失。DeepLabV3+通过引入空洞卷积,在不损失信息的情况下,加大了感受野,让每个卷积输出都包含较大范围的信息。
4.3.1 定量数据分析
使用本文方法所提出的数据集,从测试集中选取了2 400张图像进行了几何畸变校正实验。根据3 个评价指标MAE、PSNR 和SSIM 来定量地评价不同方法的校正效果,结果如表2 所示。

表2 不同方法在测试数据集上的评价结果Tab.2 Evaluation results of different methods on the test dataset
表2 的定量结果表明,本文方法在预测坐标差向量的精度、图像校正和结构恢复方面都优于其他方法,在定量评估中取得了最高分。原因有:(1)U-Net 网络相比于其他网络模型可以更好地提取畸变图像的几何特征,提高网络的学习能力;(2)空间注意力机制的应用进一步辅助U-Net网络学习图像的空间信息;(3)两种损失函数增强了网络的预测精度。
4.3.2 主观评价分析
为了进一步验证本文方法的校正效果,根据双激励损伤尺度(Double Stimulus Impairment Scale,DSIS)图像质量主观评价方法[28]设计了针对图像校正的主观评价实验,具体过程如下:
(1)数据准备。从测试数据集中按照4 种畸变类型,每类随机选择2 张棋盘格图像和3 张普通图像,共20 张畸变图像,然后选择对应的标签图像作为主观评价中的参考图像。将这20 张图像分别采用表2 中所提及的6 种方法进行校正,得到校正图像。以参考图像和每张校正图像为一组进行测试,共形成120 组测试图像对。
(2)评级划分。参考DSIS中的评级方法,采用5级评分制(1~5分)表示校正图像相对于参考图像的质量损失程度,具体等级划分说明如表3所示。

表3 评分等级说明Tab.3 Description of the grading scale
(3)评价实施。邀请20 位在校研究生参与实验,其中女生8人,男生12人,且都没有图像畸变校正相关背景。在开始实验之前,为受试者做一个简短的培训,说明评分细则,然后进行3 组测试实验,熟悉测试实验流程(测试实验不记入正式实验结果)。每位受试者观察一对测试组合(参考图像与根据所使用方法编号后的校正图像)并进行评分。
(4)评价结果。经相关性分析,将相关性系数小于0.75 的2 组数据剔除掉,接受18 位受试者的主观评价数据。计算这18 位受试者的平均意见得分(Mean Opinion Score,MOS)和方差(Variance),如表4所示。主观评价结果表明,本文方法的MOS分值最高且方差最低,说明方法的校正效果最佳且较为稳定。同时,经过T-test 的成对统计检验,本文方法的主观评价分数均显著高于其他方法(p<0.05)。

表4 不同方法主观评价分数Tab.4 Subjective evaluation scores of different methods
图4 给出了部分测试样例。在图4 中可以直观地看到本文方法在普通图像和棋盘格图像都取得了良好的校正效果,且畸变程度较大的图像边缘部分也得到了较好的校正。Hosono 方法对于测试图像整体校正效果较差,而且校正后的图像像素不平滑。其他方法对棋盘格图像都有较好的校正效果,对于普通图像,Li方法、PSPNet网络、U-Net 网络在图像的边缘校正效果明显下降,而DeepLabV3+网络则是对图像中心进行了过度的校正,导致畸变程度最小的图像中心发生了扭曲。主观观察结果与主观评价结果(表4)较为一致。

图4 主观评价实验数据的样例图Fig.4 Examples of the subjective evaluation experiment
4.4 消融实验
本节进行了消融实验研究,以评估所提出的损失函数的有效性。保持其他训练条件相同,仅改变损失函数,以MAE、PSNR、SSIM 3 种指标来定量地对比不同损失函数对网络预测的精度和畸变图像校正的影响。实验结果如表5 所示。

表5 损失函数的消融实验Tab.5 Ablation experiments of loss function
表5 结果表明,使用平均绝对误差损失L0比Li 方法中使用的EPE 损失有更高的预测精度,而且坐标差损失通过权重向量M优化可以进一步提高模型的预测精度,降低预测坐标差向量Vpred的边缘预测误差。图像的重采样损失L2同样发挥了作用,与坐标差损失L1相互补充,进一步提高了畸变图像的校正效果。
4.5 GoPro 光学影像校正
除以上在测试集上的性能验证外,还将Li 的方法、Hosono 的方法和本文的方法应用于GoPro相机获取的真实影像的校正,实验结果如图5 所示。图5(a)为使用GoPro 相机拍摄的“鱼眼”畸变的图像(压缩为352 pixel×352 pixel)、图5(b)为Li 方法校正后的图像、图5(c)为Hosono 方法校正后的图像、图5(d)为本文方法校正后的图像。从图中可直观地看出,本文方法校正效果优于其他两种方法,说明所提出方法的泛化性能较好,可以直接应用于对GoPro 相机拍摄图像的校正。

图5 GoPro 相机光学影像的校正对比实验Fig.5 Correction and comparison experiment of optical images of GoPro cameras
5 结 论
本文提出了一种混合畸变的数据集构建方法,使用深度学习的方法将畸变图像校正问题转为预测畸变图像的逐像素坐标变化问题,摆脱了传统方法中复杂的数学模型计算等问题,增加了校正方法的适用性。实验结果表明,本文方法对于普通图像和棋盘格图像都有良好的校正效果,所提出的两种损失函数对于模型预测的准确度和图像的校正都起到了重要的作用。其中,MAE 为0.251 9,SSIM 为0.930 6,PSNR 为35.796 8 dB。GoPro 影像的校正实验进一步证明了本文方法的适用性和实用性。

