面向多姿态点云目标的在线类增量学习

张润江，郭杰龙，俞 辉，兰 海，王希豪，魏 宪*

（1.福州大学 电气工程与自动化学院，福建 福州 350108；2.中国科学院 福建物质结构研究所，福建 福州 350002；3.中国科学院 海西研究院 泉州装备制造研究中心，福建 泉州 362000）

1 引 言

深度神经网络（Deep Neural Networks，DNN）已经在许多机器学习任务中取得了巨大的成功［1-3］，这些任务都是基于独立同分布（Independent Identically Distributed，IID）数据。这一设定违反了实际应用中所面临的非平稳数据分布，如自动驾驶、智能对话系统、智慧医疗和其他实时应用。面对非IID 数据，当DNN 对新任务进行再训练时，神经网络在过去任务中的性能表现会迅速下降，这被称为灾难性遗忘［4］。增量学习（Incremental Learning，IL）［5］的出现 使DNN 能够在 学习新知识的同时保留先前获得的知识，使模型具有可塑性-稳定性［6］。

传统的增量学习大都是以离线的方式训练模型，即通过重复训练多批次当前任务的数据来增加模型的拟合效果。然而，由于隐私问题或者内存限制，离线的设定不再适用。本文考虑了一项具有挑战性的单次数据流任务，即在线类增量学 习（Online Class-Incremental Learning，OCIL）［7］。OCIL 限制每个训练任务的样本流只能看到一次，并且是非IID 的。

以往IL 和OCIL 的研究对象都是具有固定姿态的样本流，即每个样本都预先进行了矫正。这种设定对自动驾驶等实时应用是不负责任的，它们在真实情况中所面临的数据流是各个姿态的，即样本特征存在平移、旋转对称变换［8］。常用的数据扩充方法［9］在面对OCIL 这种单次数据流时也变得不再适用，特别是3D 目标姿态的高复杂性对网络提出了更严格的要求。传统的神经网络只具有平移等变性［10］而不具备旋转等变性。在IL 任务中，除了新任务带来的影响外，造成遗忘的另一个重要原因是网络没能提取到目标足够的几何信息，而更多地关注到了一些无关特征，如固定的位置信息而不是目标本身之间的结构信息。保证遗忘率尽可能低首先要保证能够学到更丰富的几何特征，为此，我们基于李群引入旋转等变机制［11-13］降低网络受目标姿态的影响。同时，使用点云数据以坐标和特征值的形式出现，即，此设定可以方便网络提取目标的几何信息，且通用于2D 和3D 的数据。

常见的类增量学习方法大致分为3 大类：参数隔离方法［14-16］、正则化方法［17-19］和记忆重放方法［20-22］。参数隔离方法是通过扩展网络模型为代价提高网络的可塑性，以适应新的学习任务。随着新类别的增加，该方法将会导致参数量线性增长，从而变得不可持续。正则化方法通过添加正则项，在学习新的别类时约束参数的更新方向来避免灾难性遗忘。但正则化通常以牺牲可塑性为代价，不仅会降低对新知识的接纳程度，还增加了先前知识的遗忘率，往往表现不佳［23］。相比之下，记忆重放的方法已经比较成熟，将旧任务数据流中的少量样本存储在存储器中，并在新任务的训练中重放它们。该方法在许多具有挑战性的场景中都具有最优的表现，在IL 中发挥着关键的作用。本文在研究中采用基于记忆重放的方法。

基于以上问题，本文提出无视姿态重放方法，主要工作有：

（1）考虑更符合现实情况的复杂设定，即面向多姿态目标的在线类增量学习。

（2）提出一个通用于2D 和3D 数据的OCIL模型。基于李群引入旋转平移等变机制，使网络能够提取更丰富的几何信息，减弱目标姿态的影响，从而缓解灾难性遗忘。

（3）提出基于损失变化的记忆重放策略，在图像分类基准数据集MNIST、RotMNIST、CIFAR-10 和trCIFAR-10，3D 点云基准数据集ModelNet40 和trModelNet40 上进行了实验。本文方法在目标多姿态的设定下显著优于对比方法。

2 相关基础

2.1 类增量学习

一般情况下，类增量学习是涉及T个任务的顺序学习，这些任务由不同的类集组成，在不同学习阶段逐渐增加，且须在任何一个训练任务t中对前t-1 个任务中所看到过的类能够准确分类［24-27］，可以按以下方式设定：

其中：C表示所有类别的集合；Tt表示C中分配给任务t的子集，其由分配函数Ψ决定表示类别c的样本集；则表示任务t的样本集，且=∅。值得注意的是，不同类别c的样本集数量Mc可以相同也可以不同，本文考虑Mc相同情况下的场景。

2.2 等变性和不变性

等变性：当一个函数f：X→Y的定义域X被对称群G作用，然后计算函数f所得到的结果等同于先计算函数f，然后计算应用群G作用得到的结果一样时，我们称函数f关于变换G是等变的，如公式（2）所示：

其中，g∈G是对称群G的一个群元素。

不变性：同理，当一个函数f：X→Y的定义域X被对称群G作用，然后计算函数f所得到的结果同直接计算函数f得到的结果一样时，我们称函数f关于变换G是不变的，如公式（3）所示：

在分类任务中，我们期待的是对输入进行任何对称变换，最终得到的结果不发生变化，即不变性。通常的解决办法是将具有不变性的函数f与等变函数fk组合在一起，最终达到不变性。证明过程如式（4）所示［28］：

其中：群表示π1，…，πK分别作用于函数f1，…，fK上，且fk关 于πk，πk-1等 变，即fk∘πk-1=πk∘fk，k∈{1，2，…，K}，函数f关于πk不变，即f∘πk=f，因此f∘fK∘…∘f1是不变函数。

群等变：深度学习中最常见的等变是卷积层的平移等变性，即Lt f(x)=f(x+t)，然而却不具备旋转等变性，即Lr f(x)≠f(r∘x)。为了能处理多姿态数据，最初的办法是数据扩充［29-30］。2016 年，文献［8］基于p4 群和p4m 群首次提出了具有旋转对称性的群等变卷积神经网络。从此，关于群等变性的研究吸引了许多学者的注意。例如文献［11，31-32］提出基于SO(3)的三维旋转群，文献［33-34］提出基于SE(d)的平移旋转群，文献［35］提出基于R*×T(2)的平移放缩群等。

2.3 点卷积

本文使用通用于图像和点云的点卷积网络［36-37］，其定义如公式（5）所示：

其中：gθ：Rd→为卷积滤波器，f（·）：Rd→为输入特征图，h（·）：Rd→为输出。

离散化后如公式（6）所示：

其中：V为积分空间体积，n为正交点的数量。在例如图像的3×3 卷积层中，gθ对每个落在3×3网格上的点：（-1，-1），（-1，0），…，（1，1）都有独立的参数。

3 无视姿态重放的在线类增量学习

我们考虑一个单次数据流的类增量场景，它模拟了一个实际的设置，模型必须对每个传入的示例执行在线更新，而无需重复多次训练。在每个任务t到来时，系统从数据流中接收一组新的样本：其 中，bs 为每组 的样本 个数，xi为原输入样本，yi为样本的标签。考虑到目标的多姿态时，其输入表示为Tg xi，意为原样本发生几何变换（旋转、平移）后的结果；g为SE(d)(d=2，3)群的一个群元素，是对应几何变换的群表示。

模型结构如图1 所示，主要包含两部分：（1）可以提取丰富的几何特征的分类器θ；（2）基于损失变化的记忆重放。

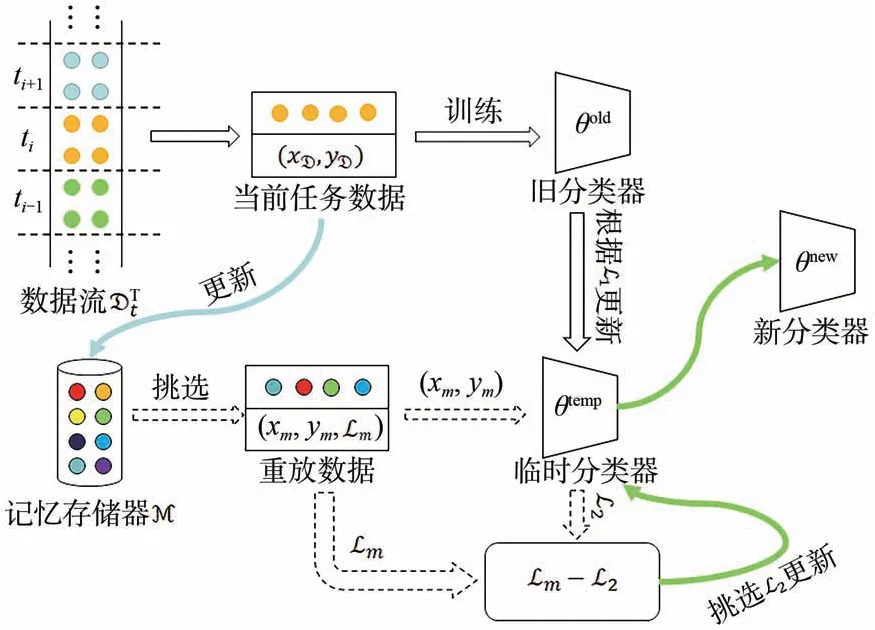
图1 模型结构图Fig.1 Model structure diagram

3.1 具有多姿态识别能力的分类器θ

为了降低OCIL 任务中网络受目标姿态的影响，同时提取更丰富的几何特征，减少灾难性遗忘，我们提出具有抗旋转平移几何变换能力的分类器，即图1 中的θ。分类器为在骨干网络PointNet++［38］上进行的改造，主要加入3 部分：点云化处理、群等变点卷积层和群全局池化层。

点云化处理负责将原输入转换成点云数据，其过程如公式（7）所示：

其中：x是原始输入，当输入是图像数据时d=2，当输入是3D 数据时d=3；y是原始输入映射到高维空间后的点云化结果，即，xi是点云坐标，其原点为输入样本的几何中心，fi为每个点所对应的特征值。例如，在CIFAR-10 数据集中，xi为（-16，16），（-15，16），…，（16，-16），对应原样本图片从左上角到右下角的坐标；fi是为原样本图片从左上角到右下角每个像素点所对应的特征值。点云化处理后的高维信息同时包含了几何位置和每个点的特征信息，使得数据特征更加丰富，从而能够更好地提取几何特征。

群等变点卷积层负责对网络进行平移旋转等变性改进。将点云化信息映射到更高维的空间以提取特征，是使网络抗旋转平移几何变换的关键，其定义由公式（8）和公式（9）给出：

其 中：g∈SE(d)，d=2 适用于xi∈R2，d=3 适用 于xi∈R3，{ui∈SE(d)：u0=x}，ni=|nbhd(i)|为每个点邻域中的点数。公式（8）只适用于点卷积的第一层，其将输入从欧式空间映射到了SE(d)所在的李代数空间，即：Z2↦SE(d)；公式（9）适用于除第一层以外的所有点卷积层，其在李代数空间进行映射，即SE(d)↦SE(d)。值得注意的是，在考虑姿态的在线类增量学习设定下，xi在不同时刻表现为不同的Tg xi，即同一个样本每次出现都会表现为不同的姿态（发生了不同的平移和旋转）。另外，由于SE(d)群是连续群，并不能穷举g的所有的情况，我们使用哈尔测度μ进行均匀采样。

点云化处理后，显式地蕴含了位置信息和特征信息。而群等变点卷积层则能够将输入映射到SE(d)所在的李代数空间，该空间融合了样本不同位置和角度的特征，能够使网络不受目标姿态的影响。同时，点卷积能够使每个点邻域范围内的特征进行聚合，表征一定范围内的几何信息，从而使网络能够提取更丰富的几何特征。

群等变点卷积层的具体实现算法流程如算法1 所示，其关于旋转和平移变换是等变的，证明过程如式（10）所示：

其中：Lt f表示对输入进行t（旋转平移）变换，第一行到第二行令x=tx。证明结果满足公式（2）中等变性的定义。

群全局池化层与普通的池化层类似，包括最大池化和平均池化等，本文使用了全局最大池化（GlobalMaxPooling，GP），其定义如公式（11）所示：

其中，gU是SE(d)的子群U上的一个g变换。对GP 层的输入进行对称变化，其输出总是不变的，即GP 具有不变性，满足公式（3），放在网络的最后用来使模型整体达到不变性的效果，相当于公式（4）中的f，其示意图如图2 所示，ki∈gU。

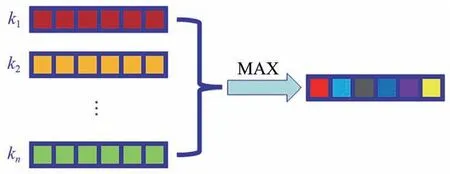
图2 全局最大池化层Fig.2 Global maximum pooling layer

3.2 基于损失变化的记忆重放

为了应对OCIL 挑战，基于记忆重放的方法在固定内存中储存少量访问过的数据，并在未来的任务中进行回放，都取得了很好的成效［7，39-40］。我们分配一个固定内存大小的记忆存储器M（容量为M），当样本流到达时，使用随机采样［41］来保证记忆的多样性，同时，储存了每个样本最近一次的损失L，即存储器中为为了保证M 中的样本均衡，在每个新类到达时舍弃一部分旧样本来储存新样本，并保证每个类别的数量相同。

记忆重放涉及的关键一步是回放样本的选择，我们采用与［7，42］类似的假设，即模型应该优先回放被忘记的样本，以减少对早期任务类别的灾难性遗忘。算法2 描述了具体的重放过程。在时刻t，旧模型θold从数据流D中接收一批数据，根据损失L1执行更新产生临时模型θtemp，如公式（12）和公式（13）所示：

其中：ℓ为交叉熵损失函数，α为学习率。接着从存储器中抽取n2≥n1组数据，根据临时模型θtemp计算损失L2，并与Lm进行比较，挑出损失变化最大的n1组L2用于更新θtemp，从而产生新模型θnew，如公式（14）和公式（15）所示：

4 实验结果与分析

4.1 实验数据集

我们使用MNIST［43］、RotMNIST［44］、CIFAR-10［45］、trCIFAR-10、ModelNet40［46］和trModel-Net40 数据集来评估本文提出的方法。其中，Rot-MNIST 数据集由62 000个随机旋转的MNIST 数字组成，旋转角度从SO(2)中均匀采样。trCIFAR-10 和trModelNet40 为我们对CIFAR-10 和Model-Net40 进行随机的平移和旋转的几何变换，模拟真实多姿态场景。MNIST、CIFAR-10、Model-Net40 用于固定姿态目标实验，如图3（a）所示。RotMNIST、trCIFAR-10、trModelNet40 用于多姿态目标的实验，如图3（b）所示。我们列出了每个数据集的实验设置：

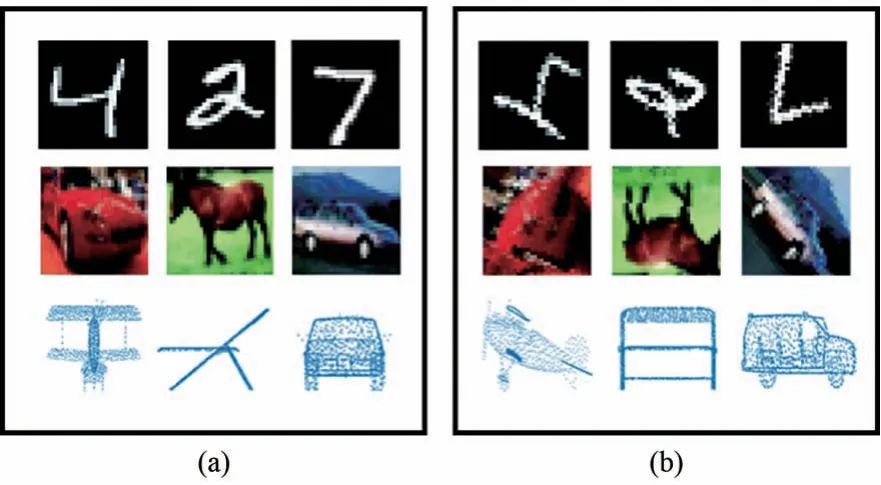
图3 固定姿态目标（a）与多姿态目标（b）Fig.3 Fixed posture target（a）and multi-posture target（b）

（1）MNIST 和RotMNIST：按照每2 类为一个任务，分为5 个不同的任务；将图片转为特征值为像素值的2D 点云输入，即，其中xi∈R2，fi∈R。遵从文献［7］的设定，每项任务分配1 000 个样本用于训练。

（2）CIFAR-10 和trCIFAR-10：按照每2 类为一个任务，分为5 个不同的任务。将图片转为特征值为像素值的2D 点云输入，即其中xi∈R2，fi∈R3。遵从文献［7］的设定，每项任务分配9 500 个样本用于训练。

（3）ModelNet40 和trModelNet40：按照每4 类为一个任务，分为10 个不同的任务；点云输入为其 中xi∈R3，fi=1。由 于Model-Net40 数据集不同类的样本数量不同，故取每类的80%用于训练，即共有9 843 个数据流用于训练。

4.2 实验环境

本文所有实验都在同一学习环境下进行，如表1 所示。

表1 实验环境Tab.1 Experimental environment

4.3 基线和评价指标

对于固定姿态目标和多姿态目标的实验，我们考虑了以下设定作为评价基线：

（1）finte-tuning：微调，在新任务到达时连续训练，不采用任何防遗忘策略，作为实验对照下限；

（2）iid online：所有任务数据同时出现并训练一次；

（3）iid offline：允许数据多次出现重复训练，作为实验的上限。

这些基线所使用的分类器都是3.1 节中具有多姿态识别能力的分类器。为了评估不同方法的效果，我们引入两个评价指标：最终平均准确率（AvgACC）和平均遗忘率（AvgF）［41］。

4.4 实验分析

我们在2D 数据集上进行了评估，即MNIST、RotMNIST、CIFAR-10 和trCIFAR-10。除 了4.3 节中提到的基线外，本节还使用了其他两种基于记忆重放的类增量学习方法作为面向2D 数据的对照实验：ER［41］和ER-MIR［7］。我们统一了记忆存储器的容量M=500，且每批数据只迭代1 次。每组实验进行了20 次并取平均值，结果如表2 所示。

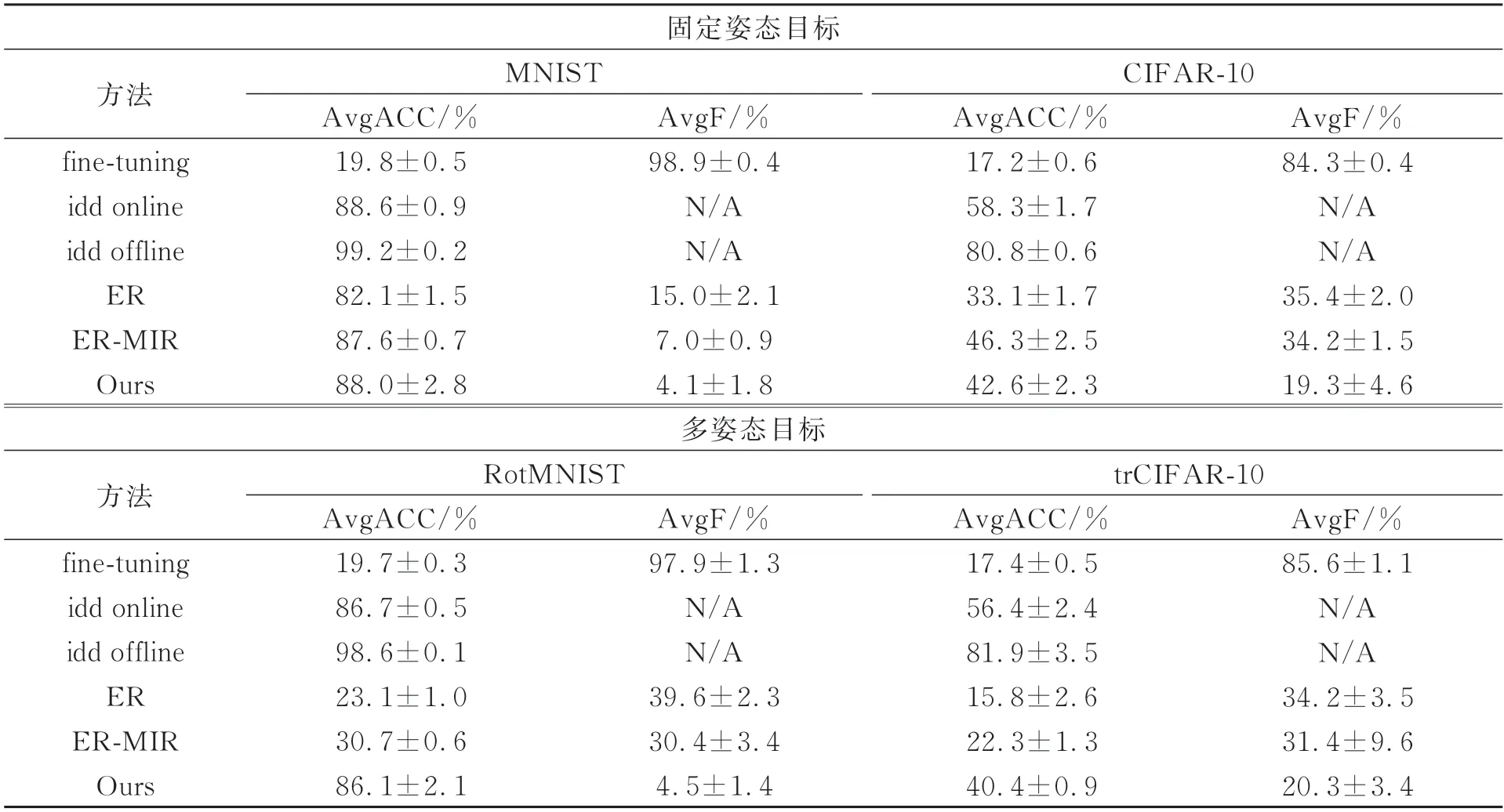
表2 2D 图像数据上的实验结果Tab.2 Experimental results on 2D image data

可以看到，当面对固定姿态目标MNIST 时，本文方法的AvgACC 和AvgF 分别为88.0%和4.1%，均优于ER 和ER-MIR 方法，且AvgACC 与基线iid online 接近，说明本文方法可以有效缓解灾难性遗忘，实现任务之间的稳定性。当面对固定姿态目标CIFAR-10时，本文方法的AvgACC 明显优于ER，与ER-MIR 相比也仅差3.7%，但AvgF明显优于ER 和ER-MIR，证明本文方法可以很大程度缓解灾难性遗忘。

而当面对多目标姿态RotMNIST 时，ER 和ER-MIR 与它们在MNIST 中的表现相比具有显著的变化，AvgACC分别下降了59.0%和56.9%，AvgF 也分别增加了24.6%和23.4%，说明ER和ER-MIR 在面对多姿态目标时均不能学习到有效信息，且遗忘率明显增加，并不适用于真实场景。而本文方法与在MNIST 中的表现相比，AvgACC只下降了约1.9%，AvgF只增加了0.4%。在20 次的实验中，本文方法的AvgACC 均保持在85%以上，证明本文方法可以有效抵抗目标姿态所带来的影响，且对灾难遗忘有明显的缓解作用。当面对多目标姿态trCIFAR-10 时，本文方法的表现与上面所述一致，受目标姿态影响很小，AvgACC 只降低了约2.2%，AvgF 只增加了1%。而ER 和ER-MIR 在面对多姿态目标trCIFAR-10时的AvgACC 不及它们在固定姿态目标CIFAR-10 中表现的1/2。虽然AvgF 并没有很大变化，甚至ER 在trCIFAR-10 中的AvgF 要略低于在CIFAR-10 中的AvgF，但这是由于ER 本身在学习中的最高准确率很低所导致。

图4中列出了本文方法和ER-MIR方法中每个任务在不同时期的分类精度对比。如图4（a～d）所示，当面对数据集MNIST 时，本文方法和ERMIR 的表现不相上下，每类任务的最终准确率都与最初的准确率相比并没有太大变化，说明本文方法和ER-MIR 在面对固定姿态目标时都能提取有效的特征，并对灾难性遗忘有很好的抵抗力，面对OCIL 这种严格的设定能保证稳定性。而当面对RotMNIST 时，ER-MIR 变得不再稳定，在后续任务中发生了灾难性遗忘，每类任务的最终准确率与初始准确率相比有明显的差距，下降到了20%～45%，远不及它在MNIST 中的表现。相比之下，本文方法在面对RotMNIST 时仍能保证最终准确率与初始准确率很小的差距，维持在76%～97%，且与在MNIST 中的表现相差无几，证明本文方法并不受目标姿态的影响，在OCIL 任务中有效缓解灾难性遗忘，具有很好的稳定性。

如图4（e～h）所示，当面对CIFAR-10 这种更有挑战的数据集时，本文方法和ER-MIR 虽然都有一定的遗忘，但它们的最终准确率也都能保持在33%以上。而当面对trCIFAR-10 时，ERMIR 的第一个任务和第二个任务的最终准确率下降至10%以下，第三个任务的准确率也下降到了20%以下，均发生了严重的遗忘。相比之下，本文方法依旧能和在CIFAR-10 中的表现一样，有效地消除了目标姿态所带来的影响，具有相对较好的稳定性。

从图4 中还可以看到，本文方法在这4 种数据集中每类任务的最终准确率相差不超过22%（分别为12%，22%，19%，18%），并没有出现由于单任务准确率高而提高平均准确率的现象，说明本文方法在OCIL 任务中不仅不受目标姿态的影响，还有很好的平衡性。

为了验证本文方法性能，我们进一步在3D数据集ModelNet40 上进行了实验。在我们的了解中，并没有发现面向3D 数据的OCIL 的相关研究，因此，本部分的对照实验只采用3.3 节中所提到的基线实验。同时，设定记忆存储器的容量M=4 000，即每个任务存储200 个样本，且每批数据依旧只迭代1 次来保持online 的设定。每组实验进行了20 次并取平均值，结果如表3 所示。可以看到，本文方法在面对多姿态目标trModel-Net40 时的性能与固定姿态目标ModelNet40 的AvgACC 和AvgF 都相差不大，分别约为4%和2%，且AvgACC 超过了基线idd online 的结果，证明本文方法在面对3D 目标时也可以做到无视目标的姿态，同时对灾难性遗忘有很大程度的缓解。

表3 3D 数据上的实验结果对比Tab.3 Experimental results on 3D data

为了评估不同姿态对OCIL 任务的影响，我们在MNIST 数据集上进行了补充实验，如图5 所示。其中，横轴表示样本的姿态变化范围，如“60”表示数据流在[-60°，60°]范围内随机旋转，以此类推，来模拟样本姿态的丰富程度。从图5 可以明显看到，随着角度变化范围的增大，ER 方法和ER-MIR 方法的AvgACC 逐渐下降，尤其在60°后有显著的下降，并最终下降到基线fine-tuning附近，可见样本姿态对传统方法有较大的影响。相比之下，本文方法的AvgACC 随着角度变化范围的增大只有较小的波动，波动范围保持在3%以内，证明本文方法可以在很大程度上降低目标姿态的影响，有很好的稳定性。

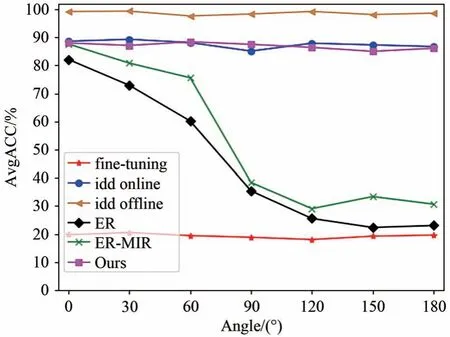
图5 MNIST 不同姿态的结果Fig.5 Results of MNIST with different postures

5 结 论

与传统增量学习不同，本文考虑了更切合实际的复杂场景，即面向多姿态目标的在线类增量学习，该设定加剧了灾难性遗忘。为了解决这个问题，本文提出了通用于2D 和3D 数据的在线类增量学习方法。该算法的网络框架基于SE（d）李群引入旋转平移等变机制，使网络可以更好地提取目标的几何信息，从而使模型不受目标姿态的影响，增加模型的可塑性。本文还提出了基于损失变化的记忆重放方法，能够配合我们的分类器缓解灾难性遗忘，在稳定性和可塑性直接得到很好的权衡。本文方法在MNIST、RotMNIST、CIFAR-10、trCIFAR-10、ModelNet40 和trModel-Net40 数据集上进行多次实验并获得了有竞争力的结果，其中AvgACC 除了在CIFAR-10 表现略低于ER-MIR 外，其余都取得了最好的结果，分别为88.0%，86.1%，42.6%，40.4%，52.8%，48.8%；AvgF 则在所有情况下都为最优，分别为4.1%，4.5%，19.3%，20.3%，22.0%，24.0%。实验结果验证了本文方法的有效性，能够同时做到不受目标姿态的影响并缓解灾难性遗忘。