基于侧窗滤波改进的神经网络非均匀性校正算法

黎明清，王宇庆，孙海江

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049）

1 引 言

红外焦平面阵列探测器（IRFPA）具有灵敏度高、帧率高、结构简单等优点，已经成为当前红外成像系统中使用的主流器件。该器件从最初的军事侦察领域逐渐覆盖医疗成像、工业检测、消防监控、自动驾驶等多种应用场景［1］，发挥着不可替代的作用。然而基于IRFPA 的红外成像系统无法避免非均匀性噪声问题。产生这一问题的主要原因包括各像元自身的响应不均匀性以及信号读出电路及放大器增益的非一致性［2］。目前的制造工艺水平短时间内无法从硬件层面上完全克服非均匀性噪声，因此在工程应用中为了提升红外成像系统图像质量必须进行非均匀性校正。

目前，非均匀性校正算法主要包括两个不同的技术路线，分别是基于定标实验的校正和场景变化的校正。定标实验算法代表方案有两点校正以及多点校正算法［3-6］。Zhang T 等人［7］提出了基于自适应多点法的sCMOS 实时非均匀性校正，通过阈值比较的方式分别确定最优分段点的位置以及最佳分段数量实现自适应校正。该类算法需要预先做黑体辐射标定实验，当环境温度改变时器件参数会发生漂移，连续工作一段时间后需要重新标定。基于场景变化的算法主要包括时域高通滤波算法［8-9］、恒定统计算法［10-11］与神经网络算法［12-16］等。Qian 等人［8］将引导滤波引入时域高通滤波算法，有效改进了“鬼影”问题与边缘退化问题。Liu 等人［10］提出一种基于分段两点校正法和局部恒定统计的联合校正方法，有效增强了恒定统计法的有效性和鲁棒性。Zhang L 等人［16］将双边滤波引入神经网络法，进一步提升了该算法对处理后图像的细节保护程度。此类算法基于场景图像的变化更新校正参数，具有无需标定实验、校正过程不需停机的优点。在基于场景变化的非均匀性校正算法中，主要考核校正后图像残留的非均匀性噪声强度、校正后图像有无“鬼影”现象以及算法的计算复杂度等方面的性能指标。

近年来，伴随着视频图像处理设备计算能力的提升，为了解决校正参数失效导致的反复标定实验问题，大量学者将研究方向转移到基于场景的非均匀性校正方式，提出了基于最优化理论计算的非均匀性校正算法。此类算法主要包括小波法、变分法、深度学习法等。2021 年，Zhang T等人［17］提出了基于小波主成分分析法，该算法从信号分解的角度寻求最优化图像信息主要成分达到去除非均匀性噪声的目的，其最大的优势在于计算速度快，适用于寻求处理效率与处理结果平衡的应用场景。2020 年，Yang 等人［18］利用各向异性变分法和低秩正则项相结合的方法提取条纹噪声，实现了噪声图像分离的非均匀性校正。2022 年，Mou 等人［19］提出了基于全卷积网络的红外图像非均匀校正算法，该网络包含非均匀性等级估计子网络和校正主网络两部分，有效避免了校正过程中出现过拟合问题。该类算法与滤波算法、统计法、传统神经网络算法相比通常有更好的校正效果，但是此类方法也存在明显的不足之处。小波分解主成分分析法、变分法数学计算复杂度较高、最优参数求解复杂。深度学习法依赖专用设备且需要大量数据集标定处理以及长时间的训练过程，修改网络结构后需要反复重新训练，不利于算法硬件实现。

神经网络法作为一种经典的基于场景变化的非均匀性校正算法，校正效果稳定、计算复杂度低，便于工程中硬件实现。但是，此类算法多数利用帧间多次迭代计算校正图像，容易出现图像模糊退化以及“鬼影”现象，影响红外探测器成像质量。本文针对这一现象，提出一种将侧窗滤波［20］与神经网络法结合的校正算法。该算法在去除非均匀性噪声的同时较同类算法能更好地抑制“鬼影”现象从而获得更好的图像质量。该算法基于传统的神经网络法改进，滤波算子采用侧窗滤波算法，计算过程与均值滤波相似，计算复杂度远低于双边滤波改进算法以及最优化算法，为小算力、低功耗移动平台实现实时非均匀性校正提供了新的研究思路。

2 神经网络校正模型分析

2.1 神经网络法工作原理

图1 为神经网络算法的结构图［12］，它的关键步骤是校正层与隐含层的设计。

输入图像序列首先要经过输入层提取单帧图像数据送往校正层，校正层读取增益校正参数与偏置校正参数完成图像序列的输出结果更新，即：

式中：xi，j表示原始图像位于(i，j)位置的灰度值，Gi，j表示相应位置的增益校正参数，Oi，j表示相应位置的偏置校正参数，yi，j表示相应位置校正后的输出结果。

校正参数的计算需要使用隐含层。隐含层的作用是产生期望图像，传统算法计算过程如式（2）所示：

式中，fi，j表示四邻域均值滤波结果。神经网络法完成非均匀性校正的关键步骤是寻求使损失函数ei，j最小的增益参数和偏置参数，损失函数的定义为：

在计算损失函数最小值时需要利用梯度下降法获得增益参数和偏置参数，即：

式中，α为迭代步长。当前帧校正后的图像与期望图像之间的损失函数数值增大时，网络结构立即向减小损失函数方向传播校正参数G、O的迭代结果，用于下一帧校正图像计算，实现基于场景的自适应校正。

2.2 图像模糊与伪影现象

传统的神经网络法利用均值滤波获取待校正像素点的期望值。均值滤波可以有效去除场景图像中的高频非均匀性噪声，同样也会去除图像中的边缘细节。在图像的非边缘区域，待校正像素邻域内的灰度差值较小，主要由噪声信号引起；而在图像的边缘细节位置，邻域内的灰度差值较大，均值滤波会降低边缘灰度梯度，引起图像模糊退化。为了使期望图像更加准确，有学者提出了使用双边滤波［16］、引导滤波［21］以及非局部均值滤波［22］等结果作为期望图像。上述算法在一定程度上能够达到更好的校正效果，但是上述保边滤波算法都是根据邻域内的像素灰度值相似程度赋予滤波权重，并没有考虑真实边缘的空间分布特征，无法从噪声分布的结构特征上对图像进行保边滤波处理，并且随着保边效果的提升，计算复杂度也大幅度提升，难以在小算力、低功耗移动平台实现实时校正。

同时，对单幅图像完成非均匀性校正后需要将期望图像与校正图像做差后利用梯度下降算法获得校正参数，反向传递至下一帧用于校正图像。如果图像序列相邻帧之间元素移动过快，沿着物体运动方向会残留上一帧未移动图像校正参数，此时校正区域已经没有待校正目标，就会出现明显的拖影现象。

通过上文分析可知，红外图像非均匀性校正出现模糊和伪影与两个因素有关，即期望图像获取和帧间校正参数误差传递。本文将从这两个方向出发，对传统算法进行改进。

3 神经网络校正模型改进

3.1 基于侧窗滤波改进的期望图像获取

侧窗滤波［20］算法由殷慧、龚元浩等在2019 年提出。该算法可以有效解决传统滤波算法造成图像边缘模糊问题。通常为了简化计算，在离散的情况下只定义8 个侧窗，如图2 所示。

图2 3×3 侧窗滤波算子Fig.2 3×3 side window filter operator

图2 中NW 表示左上侧窗，L 表示左侧窗，U表示上侧窗，NE 表示右上侧窗，SW 表示左下侧窗，D 表示下侧窗，R 表示右侧窗，SE 表示右下侧窗。每个侧窗中绿色区域表示侧窗滤波有效区域，红色区域表示侧窗滤波无效区域。

侧窗滤波计算过程可以表示为：

式中：wij表示像素i的侧窗内像素j的影响权重，q表示像素点的灰度值，Nn表示侧窗内权重之和，S表示侧窗覆盖的范围，In表示第n个侧窗的输出结果。8 个侧窗在离散的角度覆盖了图像在该点边缘的所有可能几何形状，从中取出与原始图像边缘最相近的侧窗输出结果作为校正输出结果，就可以实现根据边缘分布的结构特征对图像进行保边滤波。在数值计算中，取侧窗输出与原始图像在该点的灰度值之差的最小结果表示正确边缘形状，即：

式中，Im表示侧窗滤波输出结果。经典的侧窗滤波技术的边缘保持性能良好，但正是其十分出色的保边效果导致残余条纹噪声明显，因此在非均匀性校正问题中直接使用该算法也有着明显的缺点。

本文在侧窗滤波的基础上设计去噪强度参数θ。传统侧窗滤波在有效区域内权重均衡，在无效区域内权重为0。引入去噪参数θ表示无效区域像素权重与有效区域灰度权重的比值，θ越大去噪效果越明显，但边缘保持效果会下降。当θ=1 时，改进的侧窗滤波算法等价于对图像做均值滤波；当θ=0 时，改进侧窗滤波算法等价于经典侧窗滤波算法。图3 所示为θ=0.5 时改进后的NW 侧窗权重参数。通过改进可以在保留侧窗滤波边缘保持优势情况下，将边缘周围图像信息适度引入边缘计算，达到去噪效果与保边效果的平衡。

图3 改进的3×3 侧窗滤波算子Fig.3 Improved 3×3 side window filter operator

3.2 局部发散校正参数的饱和非线性抑制

在对校正参数反向传递之前，首先必须要明确校正参数是否发散，无效的校正参数传递会影响校正后图像质量。

如式（8）所示，分析目标所占像素点区域大小与滤波器宽度关系可知，使用直径为dFLTR的滤波器能保护的最小边缘如图2 中最小的绿色区所示。定义该区域最小有效边缘直径为dValid，若红外图像中目标小于最小边缘dValid，校正参数帧间迭代过程中除了包含非均匀性噪声外，还包含边缘信息，导致该点参数值过大而发散，如图4 所示。无效的局部矫正参数会对图像产生过度校正，在图像序列中的表现就是移动拖影现象。

图4 小目标校正参数的发散（图中尖峰位置）Fig.4 Divergence of small target correction parameters（peak position in the figure）

针对图中微小细节边缘滤波后导致的校正参数发散现象，本文使用一种饱和非线性特性函数抑制校正参数上限，算法原理如式（9）所示：式 中：Ei，j(f)为当前帧中位 于(i，j)位置的校正参数输入信号；Xi，j(f)为当前帧相应位置的校正参数饱和特性输出信号；Emax(f)表示当前帧饱和非线性特性的输出阈值，该值的确定需要统计当前输入图像全局最大相邻列像素点灰度均值的差值，非均匀性校正目的在于减小各列响应不均匀性，因此该参数不应当超过原始误差图像中相邻非均匀性列之间的最大灰度差值，从而实现视觉上的一致性。

校正参数在Emax(f)的范围内是线性区，取线性增益为k。当超过线性区进入饱和区，输入的校正参数继续增大时，其输出量趋于0，直到当前位置像素点不再作为图像弱小边缘区域，校正参数会重新进入线性区，继续经过迭代更新适应新的场景变化。改进后的神经网络校正模型如图5 所示，期望图像采用含去噪强度参数的侧窗滤波器获取，校正参数的更新引入饱和非线性特性阈值函数修正。

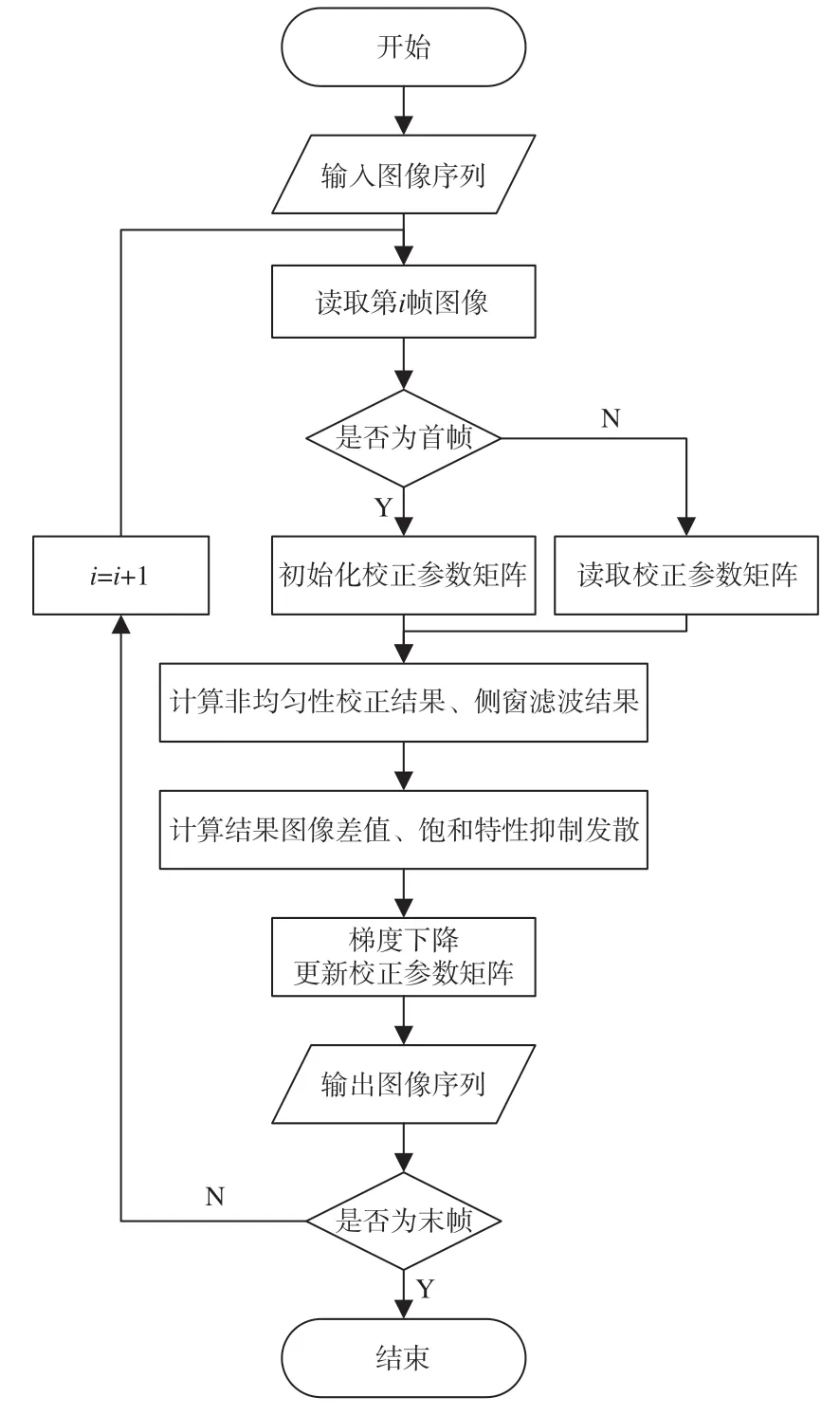
图5 改进后的神经网络模型流程框图Fig.5 Flow chart of improved neural network correction algorithm

4 实验与结果分析

4.1 实验设备

本文所有实验运行计算机系统为Win10（CPU Intel Core i5-7300HQ 主 频：2.30G，内存8G），所有的算法均利用Matlab2018a 编程实现。

4.2 算法对比及质量评价

考虑算法的硬件易实现性，将本文所提算法与经典神经网络算法［12］、Zhang L 等人［16］提出的基于双边滤波改进算法以及Zhang T 等人［17］提出的基于小波主成分分析法这3 种校正算法进行比较。在实验中共采用3 组不同环境下的红外相机拍摄图像，分别为序列1：天空背景弱小飞机跟踪目标序列［23］，共599 帧；序列2：地面复杂背景弱小飞机目标图像序列［23］，共400 帧；序列3：道路行人检测红外图像序列［24］，共400 帧。

图6 展示的是序列1 原始图像，图像分辨率为256 像素×256 像素。该序列背景纯净单一，靶机目标小，运动速度快，图像信噪比较低，校正过程中应主要防止高速运动的小目标拖影现象。

图6 序列1 原始图像Fig.6 Sequence 1 original images

图7 展示的是序列1 的非均匀性校正实验结果。从视觉效果上看，传统的基于均值滤波的校正算法具有很强的平滑作用，但是在目标边缘产生大量鬼影，如图7（a）所示，在靶机附近及右侧出现的黑色阴影即为校正过程中引入的“鬼影”，该现象在目标高速移动时尤为明显。基于双边滤波的校正算法在边缘保持以及鬼影抑制效果都有明显提升，但如图7（b）所示，通过肉眼仍可以观察到有残留的非均匀性噪声，在靶机的右侧也存在微弱的“鬼影”现象，并且靶机的机翼与中间部位的对比度相比原图有所下降。基于小波主成分分析的校正算法是针对单帧图像进行校正，不会产生帧间迭代“鬼影”现象，但由于低信噪比图像噪声主成分仍包含较多噪声信息导致该算法残留非均匀性噪声较多，如图7（c）所示，图中飞机局部放大图像中存在肉眼可见非均匀性噪声。图7（d）为本文提出的改进校正算法的校正结果。对比输入图像序列，本文算法的非均匀性噪声去除效果好，校正后图像没有明显的纵向条纹噪声。对比文献［12］、文献［16］所用校正算法，本文算法的鬼影现象有明显改善，细节边缘保持程度也达到双边滤波效果，特别是在靶机机翼位置与中间位置的对比度更接近原始图像序列，明显优于文献［16］所用算法。对比文献［17］所用算法，本文算法的残余非均匀性噪声明显降低，图像细节保护程度无明显差别。

图7 不同算法对序列1 图像的校正效果对比Fig.7 Comparison of correction effects of different algorithms on sequence 1

为了进一步评估3 种校正算法，本文引入列均值［25］与图像粗糙度指标ρ［26］进行定量评估。图像粗糙度ρ的定义为：

式中：h1=［-1，1］为图像在水平方向的卷积核模板，h2=［-1，1］T为图像竖直方向的卷积核模板，I表示输入图像，‖ ‖表示取1 范数运算，*表示做卷积操作。列均值指标反映图像在各通道增益及偏置的不均匀性，该指标的变化曲线越平坦说明图像均匀性越好。图像粗糙度反映图像整体灰度值的均匀性程度，该指标越低说明图像均匀性越好。

从图8（a）中可以看出，原始图像在90～120 列存在明显的平均值波动，表现在图像上就是明暗相间的条纹噪声。经过文献［12］算法处理后，各列均值波动幅度明显下降。文献［16］算法因为使用双边滤波获取期望图像，处理后各列均值波动幅度较传统算法略大，整体波动幅度较原始图像序列有明显改善。文献［17］算法使用小波分解后的主成分分析分离非均匀性噪声，在针对低信噪比图像的处理过程中残留有较大的非均匀性，导致各列均值波动幅度降低程度有限。使用本文提出的改进算法校正后，图像的各列均值过渡平坦，没有明显波动情况，处于另外两种算法幅度变化的包络曲线之中，说明相比经典神经网络校正算法、基于双边滤波改进的校正算法以及基于小波主成分分析算法所获得的列均值更稳定。从图8（b）中可以观察到，经过文献［17］算法处理后，图像的整体粗糙度最大，但是该算法由于不涉及帧间迭代过程，所以从第一帧开始算法效果就趋于稳定，而其他3 种算法在经过约80 帧图像数据迭代过程后才趋于稳定。经过文献［16］算法处理后，图像的整体粗糙度明显降低。经过本文算法校正后，粗糙度指标明显低于基于双边滤波改进的校正算法，与文献［12］所提经典校正算法的粗糙度指标相似，说明相比经典神经网络校正算法、基于双边滤波改进的校正算法以及基于小波主成分分析算法，本文方法的图像整体均匀性最好。

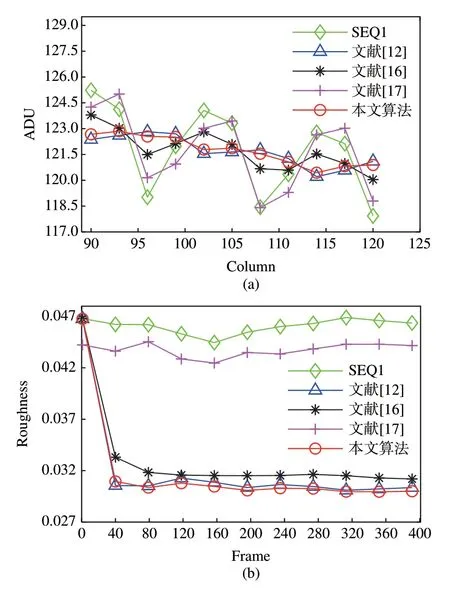
图8 （a）序列1 列均值曲线；（b）序列1 粗糙度曲线。Fig.8 （a）Sequence 1 mean curves；（b）Sequence 1 roughness curves.

由上述分析可知，本文提出的基于侧窗滤波改进校正算法在迭代效果趋于稳定后的图像视觉效果、列均值指标、粗糙度指标均优于另外3 种对比算法，综合考虑，本文算法针对图像序列1 的校正效果是4 种方法中最好的。

图9 展示的是序列2 原始图像，图像分辨率为256 像素×256 像素。该环境下背景复杂、图像对比度低、靶机目标小且运动快，图像信噪比较低，校正过程中应主要避免背景轮廓过度退化以及“鬼影”现象。

图9 序列2 原始图像Fig.9 Sequence 2 original images

图10展示的是序列2非均匀性校正实验结果。从图10（a）中可以看出，使用经典校正算法处理后的图像序列中非均匀性噪声有明显改善，但是沿着飞机移动方向存在明显拖影现象，并且由于镜头移动，复杂场景中房屋位置周围也产生了明显的“鬼影”。使用基于双边滤波改进的校正算法无明显“鬼影”现象，但是图像整体存在微弱的残余噪声，如图10（b）所示。基于小波主成分分析的校正算法属于单帧法，不会产生帧间迭代“鬼影”现象，但校正后图像仍残留明显非均匀性噪声，如图10（c）所示，图中房屋处局部放大图像中存在肉眼可见的非均匀性噪声。图10（d）为使用本文提出的校正算法的校正结果，对比输入图像，本文算法的非均匀性噪声去除效果较好；对比文献［12］算法，“鬼影”现象有明显的改善；对比文献［16］、文献［17］算法，残余非均匀性噪声有明显改善，在边缘保持方面达到双边滤波改进的水平。

图10 不同算法对序列2 图像的校正效果对比Fig.10 Comparison of correction effects of different algorithms on sequence 2

从图11（a）中可以观察到，原始图像在90～120 列存在明显的平均值波动。经过文献［12］算法处理后，各列均值波动幅度下降明显。经过文献［16］算法处理后，均值波动幅度略大于传统校正算法。经过文献［17］算法处理后，均值波动幅度较原始图像数据有所降低，但仍存在较大的列间差异性。使用本文改进算法校正后，图像在各列均值性能均优于另外3 种校正算法，列均值指标均位于经典神经网络校正算法、基于双边滤波改进的校正算法以及基于小波主成分分析校正算法的相应指标包络线内，校正结果稳定。从图11（b）中可以看出，复杂背景下场景快速运动序列的图像粗糙度在时间轴上呈现波动趋势。场景的剧烈变化引起校正参数波动，导致传统神经网络算法、基于双边滤波改进算法和本文算法3 种校正算法校正后的粗糙度相近，基于小波主成分分析的校正算法同样因为图片信噪比低而呈现较高粗糙度。分析曲线可知，在整体上本文算法校正后的图像粗糙度低于文献［16］、文献［17］所用算法，略大于文献［12］所用算法。

图11 （a）序列2 列均值曲线；（b）序列2 粗糙度曲线。Fig.11 （a）Sequence 2 mean curves；（b）Sequence 2 roughness curves.

由上述分析可知，本文提出的基于侧窗滤波改进的校正算法在视觉效果上优于文献［12］、文献［17］算法，与文献［16］算法无明显区别。列均值指标优于其余3 种对比算法。图像粗糙度指标优于文献［16］、文献［17］算法，与文献［12］算法无明显区别。综合考虑，本文算法针对图像序列2 的校正效果是4 种方法中最好的。

图12 展示的是序列3 的原始图像，图像分辨率为1 024 像素×512 像素。该环境下，目标边缘细节复杂，图像信噪比较高，场景运动缓慢，校正过程中应主要避免目标复杂轮廓过度退化。

图12 序列3 原始图像Fig.12 Sequence 3 original images

图13展示的是序列3非均匀性校正实验结果。从图13（a）中可以看出，使用经典校正算法处理后的图像序列的非均匀性噪声去除效果明显，如放大图中路面停止线处所示。图像在整体上有明显的模糊退化现象，局部存在细节丢失，对比度下降问题，如图中放大后的市政护栏已经无法分辨出内部栏杆的边缘。从图13（b）中可以看出，使用基于双边滤波改进的校正算法后，图像清晰度较传统算法有明显改善，图中放大后的市政护栏的内部栏杆边缘清晰可见，与原始图像序列无明显差异，但该算法也存在肉眼可见的残余非均匀性噪声问题，如放大图中路面停止线处所示。从图13（c）中可以看出，使用基于小波主成分分析算法校正后，图像非均匀噪声去除效果明显，图像边缘细节保持性强，局部放大图中栏杆细节保存完好，可见该算法在处理高信噪比图像时具有良好性能。但是由于小波分解后，最优主成分替换图像原始信息，在原图中部分无噪声区域形成少量明暗斑纹。图13（d）为本文提出的改进校正算法的校正结果。对比输入图像序列，本文算法的非均匀性噪声去除效果较好，校正后图像没有明显纵向条纹噪声。对比文献［12］所用算法，图像清晰度有明显改善。对比文献［16］所用算法，有效减少了残余非均匀性噪声现象，在边缘保持与细节保护方面达到基于双边滤波改进的算法校正效果。对比文献［17］所用算法，在边缘保持性能上略有降低，图像整体一致性高，没有引入新的明暗斑纹。

图13 不同算法对序列3 图像校正效果对比Fig.13 Comparison of correction effects of different algorithms on sequence 3

从图14（a）中可以看出，原始图像在595～605列存在明显的平均值波动。经过文献［12］算法处理后，各列均值波动幅度明显下降。经过文献［16］算法处理后，均值波动幅度略大于传统校正算法。使用文献［17］算法处理后，均值波动幅度整体较原始序列有所下降，且没有迭代过程，经过第一张输入图像校正后即达到稳定状态，但整体仍存在较大波动幅度。使用本文改进算法校正后，图像在各列均值性能优于另外3 种校正算法，列均值指标均位于经典校正算法、基于双边滤波校正算法和基于小波主成分分析算法相应指标包络线内，校正结果稳定。从图14（b）中可以观察到，经过文献［17］算法处理后，图像的整体粗糙度最大；经过文献［16］算法处理后，图像的整体粗糙度略高于本文算法；经过本文算法校正后，粗糙度指标略高于文献［12］所提经典校正算法过度平滑后的粗糙度指标。

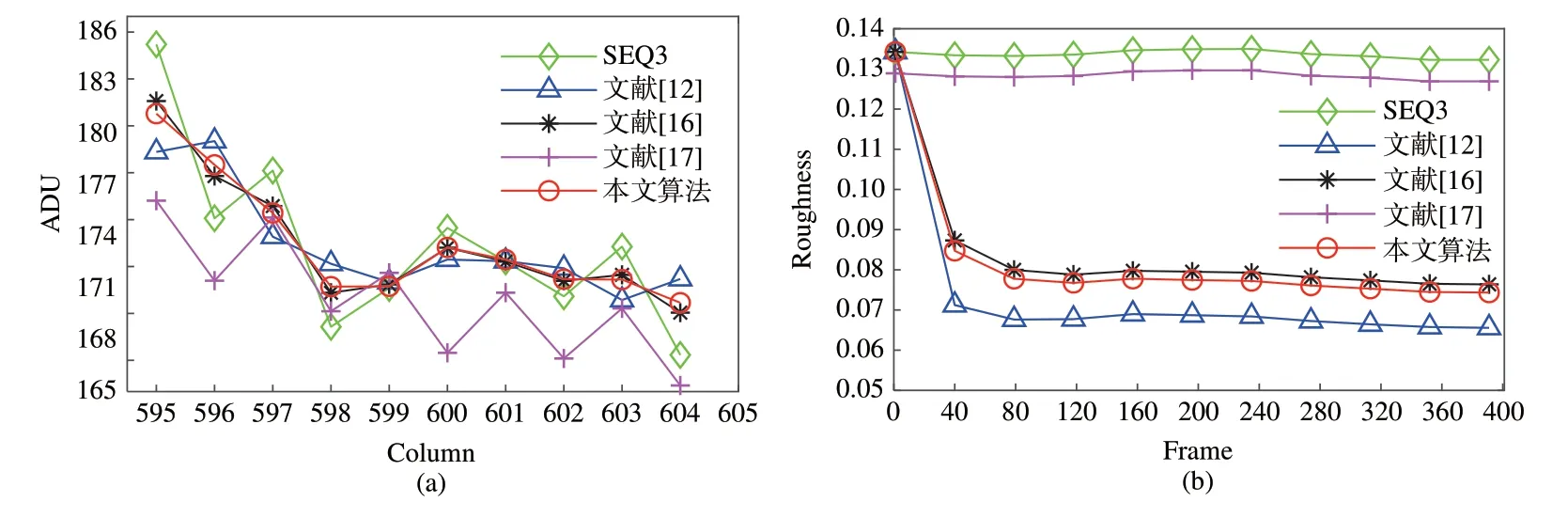
图14 （a）序列3 列均值曲线；（b）序列3 粗糙度曲线。Fig.14 （a）Sequence 3 mean curves；（b）Sequence 3 roughness curves.

由上述分析可知，本文提出的基于侧窗滤波改进的校正算法在列均值指标性能优于另外3 种对比算法；视觉效果明显优于传统神经网络算法与基于双边滤波改进算法；边缘保持程度略低与文献［17］小波主成分分析算法；图像粗糙度指标优于文献［16］、文献［17］算法，低于文献［12］算法过度平滑后的结果。综合考虑，本文算法针对图像序列3 是4 种方法中效果最好的。

表1 统计了3 组图像序列中第80～400 帧图像粗糙度ρ的平均值，该指标越低表明图像一致性越好。从表1 可以看出，基于小波主成分分析算法使用单帧图像校正，校正后的低信噪比图像粗糙度指标下降幅度小，高信噪比图像粗糙度指标下降明显，但该算法在粗糙度指标整体表现不足，各项数据均高于对比算法。本文提出的基于侧窗滤波改进校正算法在3 组测试序列中均表现出良好性能，其中在测试序列1、测试序列2 中粗糙度指标为4 种校正算法中最低，在测试序列3中该指标明显低于双边滤波改进的神经网络算法与基于小波主成分分析算法，高于传统神经网络校正算法，但是传统神经网络算法存在严重的模糊退化，过度的平滑性能导致该算法产生大量的“鬼影”，不能适用于真实检测环境。

表1 不同算法处理后的图像序列平均粗糙度指标对比Tab.1 Comparison of average roughness indexes of image sequences processed by different algorithms

表2 统计了3 组图像序列中处理400 帧图像的耗时。该指标涉及两个影响参数，即算法计算复杂度和输入图形序列像素尺寸。分析表2 中的数据，横向对比可知对于相同输入图像序列，本文所提算法处理相同帧图像耗时略长于传统神经网络算法，明显优于基于双边滤波改进的非均匀性校正算法，与基于小波主成分分析法相比也有一定优势。纵向对比4 种算法处理速度相对于不同尺寸输入图形序列可知，传统神经网络算法、基于小波主成分分析算法和本文所提算法的耗时与图形尺寸接近线性关系，而基于双边滤波改进的神经网络算法在处理高分辨率图像时耗时增加严重，原因是双边滤波器计算复杂度是输入图像空域尺寸平方项函数关系，该特性限制了算法的硬件实现。综上可知，在处理速度方面，传统神经网络算法优于本文算法；基于小波主成分分析的校正算法处理时间与本文提出算法较为接近，表明该算法优势在于平衡处理速度和处理后图像效果；基于双边滤波算法时耗性能最差。

为满足红外成像器件非均匀性校正实时性要求，需要处理速度大于视频图像输入速度。通常监控录像机系统视频输入接口帧率为25 帧/s，单帧耗时不超过40 ms。针对256×256 分辨率图像序列，传统神经网络算法处理一幅图像耗时约为7.5 ms，双边滤波改进算法耗时约为275 ms，小波主成分分析算法耗时约为35 ms，本文所提算法耗时约为12.5 ms；针对1 024×512 分辨率图像序列，传统神经网络算法处理一幅图像耗时约为25 ms，双边滤波改进算法耗时约为1 900 ms，小波主成分分析算法耗时约为175 ms，本文所提算法耗时约为95 ms。可见在基于CPU 处理器运算平台上，传统神经网络算法、小波主成分分析算法、本文所提算法满足小分辨率图像的实时校正，大分辨率图像仅有传统神经网络算法满足要求。为进一步提升算法的处理效率，实现小算力、低功耗移动平台的实时非均匀性校正，可采用现场可编程门阵列（FPGA）流水线处理实现并行加速，而小波主成分分解算法中涉及最优化主成分计算过程，FPGA 硬件实现较为复杂，不利于实现实时非均匀性校正。综合表1 和表2 可以看出，本文算法在非均匀性校正效果和算法运行效率方面都具有明显优势。

5 结 论

本文提出了一种基于侧窗滤波技术改进的神经网络非均匀性校正算法。该算法通过改进的侧窗滤波技术获得期望校正图像，通过帧间饱和非线性函数抑制校正参数局部发散，优化了传统神经网络算法的保边效果，能够有效避免校正后图像出现“鬼影”问题，降低了基于双边滤波改进算法的计算复杂度，较基于小波主成分分析算法更适用于不同信噪比的图像序列且处理速度更快。实验结果表明，本文提出的算法在测试图像序列1 上的平均粗糙度为0.030 3，连续处理400 帧图像耗时4.938 5 s；在测试图像序列2 上的平均粗糙度为0.058 6，连续处理400 帧图像耗时4.916 2 s；在测试图像序列3 上的平均粗糙度为0.079 2，连续处 理400 帧图像耗时37.417 0 s。该算法在3 组测试图像序列中平均图像粗糙度降低了30.17%，平衡处理时间与处理后图像质量性能优于对比算法，在运算时间上有显著提升。目前所提算法面临的最大问题是如何进一步提高运算速度，实现高分辨率红外图像实时非均匀性校正。而在该算法中使用的关键步骤侧窗滤波本质为多次加权均值滤波，便于FPGA 并行加速处理，因此本文也为小算力、低功耗移动平台实现实时非均匀性校正提供了新的研究思路。