基于差动共焦的倾角测量传感器

王廷煜，王之一*，杨永强，糜小涛，王建立*，姚凯男，程 雪

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049；3.吉林省智能波前传感与控制重点实验室，吉林 长春 130033；4.中国科学院 苏州生物医学工程技术研究所，江苏 苏州 215163；5.济南国科医工科技发展有限公司，山东 济南 250102）

1 引 言

光学自由曲面一般具有不对称、不规则的形状特征［1］。其相比于球面镜和非球面镜，形状更加复杂，在设计时有更大的自由度［2］，在诸多领域有着广泛的应用，如交通运输［3］、遥感［4］以及生物传感技术。但是受其检测难度的影响，尤其是缺乏有效的高精度检测手段，自由曲面的制造和大规模应用受到了限制［5］。

轮廓仪是对大口径自由曲面进行面形检测的通用检测手段［6］，检测方式主要分为接触式测量和非接触式测量［7］。接触式测量法利用触针与待测面之间的接触进行待测面位置的测量。非接触式测量法通常使用光学探针，由于其在测量时避免了与待测表面的接触，降低了划伤待测面的风险，在自由曲面测量领域获得了广泛应用［8］。

差动共聚显微镜（LDCM）是一种理想的非接触式光学探针［9］。LDCM 起源于反射式共聚焦显微镜［10］，在保留共聚焦显微镜的非接触优势［11］的同时，增强了系统的抗扰动能力以及轴向分辨率。在利用显微镜对待测面进行测量时，光束能够精准聚焦到待测面表面，即差动共焦传感器能够测量待测面的绝对位置，以及在线性区间内实现待测面跟踪。差动共聚焦显微镜利用差分信号过零点附近的轴向响应曲线，通过过零点的求解实时获取被测点的轴向位置。激光差动共焦显微技术相比于传统的共焦显微技术，对焦点位置有更强的定位能力。

轮廓仪在进行数据采集的过程中，非接触式探针在多个维度的运动机构的携带下，对待测面表面轮廓进行采样。Khairi 等人［12］使用五自由度相机，提取待测面法向量进行曲面重建。Pan 等人［13］利用空间位置和法向量对复杂曲面进行重构。相比于仅使用测量位置的三维坐标，使用待测面的法向量进行曲面重建，对于待测面上存在的微小缺陷有着更好的检测能力［14］。

已有众多学者针对利用非接触光学探针进行待测面倾斜角度测量开展了相关研究。Wu等人［15］利用衍射图像显微镜（DIM）收集不同表面方向的衍射图像，利用神经网络学习衍射图像与其相应的表面方向之间的映射关系。Pribosek 等人［16］提出了一种利用孔径编码的共聚焦显微镜测量倾斜表面时，样品表面的反射光束被设计的孔径部分阻挡，通过测量每个子孔径的能量比例获取待测面的倾斜角度。Wang 等人［5］在差动共聚焦显微镜系统中加入一对空间正交的双柱面镜结合线阵CCD的结构，将二维寻峰问题转化为一维数据的峰值提取问题。但是以上方法都存在结构复杂、系统装调难度大的问题，难以应用到实际生产中。

针对激光差动共焦显微技术无法在测距的同时测量待测面倾角的问题，本文提出了一种通过分析显微镜光瞳面光强分布获取待测面倾斜角度信息的方案。利用差动响应曲线过零点将待测面精确定位到显微镜焦点位置，使用面阵相机采集显微镜光瞳面单帧光斑图像，采用峰值提取算法提取光斑峰值位置，建立峰值位置与待测面倾斜角度之间的映射关系。实验证明，本系统赋予了传统的差动共焦测距传感器测量倾角的能力，具有结构简单、测量速度快和检测精度高的特点。

2 系统构成及其工作原理

2.1 系统结构

系统在传统差动共焦测距显微镜的结构中加入面阵相机，赋予其对待测面倾角进行测量的能力。图1 为基于激光差动共焦显微技术的倾角测量传感器测量原理及其结构图。从激光器出射的平行光束通过偏振分束镜和1/4 波片，再由显微物镜将光束聚焦到待测表面。显微镜可在物镜定位器携带下沿显微镜轴向移动，实现轴向扫描。经待测面反射的光束从显微镜光瞳面出射后，由非偏振分束镜以1∶1 的比例，分为两路光束，分别进入差动测距单元和倾角测量单元。

图1 系统测量原理及其结构图Fig.1 Principle of the system measurement and its structure diagram

差分测距单元利用非偏振分束镜将聚光透镜出射的光束等分为两份，分别进入偏离聚光透镜焦平面相同距离的两个焦前针孔探测器和焦后针孔探测器，对光束能量进行测量［17］。当待测面处在显微镜焦点位置时，两个探测器能量相等。利用物镜定位器轴向扫描，采集两个探测器的信号强度，得到差动响应曲线，如图1 右下角所示。将显微镜移动到差动响应曲线的过零点，可以实现对待测面位置的精准定位。

倾角测量单元利用当待测面处在显微物镜焦点位置时，从显微镜光瞳面出射的光束为平行光束，使用面阵相机对光束的场强分布进行探测。当待测面处于不同倾斜角度时，由于待测面上的反射光会从不同位置重新进入显微镜，相机端接收会采集到不同形状的光斑图像。利用光斑和倾斜角度之间的映射关系，对待测面倾斜角度进行检测。

2.2 系统的工作原理

为模拟系统工作原理，建立了菲涅尔衍射积分模型。设从光源出射的平行光束符合半径为r（光束能量下降到中心强度I1的1/e2处，距离光束中心的距离）的高斯分布。进入显微镜光瞳面平行光束光场分布U1(x1，y1)为：

当待测面放置在偏离显微物镜焦点距离u处时，待测面上的光场分布U2(x2，y2，u)为：

其中：m2为常数，f1为显微物镜的焦距，光波数k=2π/λ，λ为光源波长，P1(x1，y1)为照明路径上显微镜的瞳函数。

聚焦光束经过倾斜待测面反射后，重新到达显微镜光瞳面。通过向待测面光场分布中加入不同的相位，改变波前形状来模拟倾斜反射。出射方向上，显微镜光瞳面光场分布U3(x3，y3，θ，φ)为：

其中：m3为常数，θ为待测面倾斜程度，φ为待测面的倾斜方向，P3(x3，y3)为检测路径上显微镜的瞳函数。

显微镜出瞳面的光束经过聚光透镜聚焦后，分别进入焦前针孔探测器和焦后针孔探测器。探测器上的光场分布U4(x4，y4，-um)和U5(x5，y5，+um)分别为：

其中：m4为常数，f2为聚光透镜的焦距，um为针孔探测器的离焦量。

Df为焦前针孔探测器有效探测区域，Db为焦后针孔探测器有效探测区域。令焦后焦前针孔探测器信号强度作差，得到差动响应信号Idiff(u，um)：

差动响应曲线在待测物处于显微物镜焦点位置时存在唯一的过零点。并且差动响应信号在过零点位置有极高的信噪比，信号在过零点附近保持良好线性，因此利用差动响应信号能够对待测面精确定位。利用轴向扫描装置，将待测面定位到显微镜焦点位置后，再利用相机采集检测路径上显微镜光瞳面上的光斑图像。

图2 展示了不同倾斜角度下相机端的光斑图像。当待测面表面呈现不同倾斜角度时，采集光斑图像会呈现不同的形状，分析光斑图像的峰值位置，建立倾斜角度与光斑峰值位置间的对应关系。在实际测量时，利用采集单帧光斑图像，即可分析得到对应待测面的倾斜角度。

图2 不同倾斜角度下光斑峰值位置发生偏移示意图Fig.2 Changes of peak position of light spot at different tilt angles

3 改进Meanshift 峰值提取算法

Meanshift 算法被广泛应用于目标跟踪、信号峰值提取领域中。使用可在图像空间中滑动的窗口，在移动过程中，通过概率密度估计，持续进行目标方向以及位置的预测，逐级定位图像中目标所在区域。相机端采集光斑图像，在光斑能量最强处存在唯一的峰值位置，可以采用Meanshift算法对峰值位置进行提取。

3.1 核函数

Meanshift 算法通过核密度估计，指引滑动窗口移动到概率密度的极大值处。概率密度估计的方法分为有参数密度估计和非参数密度估计两种［18］。有参数密度估计，需要根据检测目标的具体形式，设置密度估计模型中的未知参数。非参数密度估计采用包含核密度函数的滑动窗口去逼近目标位置［19］。

核密度估计法属于非参数估计方法的一种。在对光斑峰值位置进行定位时，选用高斯核函数［20］，越接近滑动空间中心的数据，被赋予的权重值越高。而越远离滑动空间的中心数据，被赋予的权重值越低。设(Ph，Pv)为滑动窗口中心位置，h为核函数半径，则图像中任意位置(i，j)数据权重值为：

3.2 滑动窗口半径

滑动窗口的半径决定了滑动窗口的作用范围。选取的半径越大，滑动窗口所包含的数据量越大，鲁棒性越强，但是会导致峰值位置的定位精度不高。选取较小的半径，峰值位置定位准确，但是容易受到局部峰值的干扰，使滑动窗口收敛到错误的峰值位置。所以，本文提出了一种自适应调节滑动窗口的方法。先使用较大的滑动窗口初步定位峰值位置，再使用较小的滑动窗口精确定位光斑图像峰值位置。

采用公式（8），确定滑动窗口在本轮迭代中使用的窗口半径：

其中：ΔL是上一轮迭代中滑动窗口的移动量，hmin是设置的滑动窗口半径阈值下限，hmax是设置的滑动窗口的半径阈值上限。利用上一轮滑动窗口的移动量作为度量滑动窗口与目标位置之间距离的指标，自适应调节滑动窗口半径。在ΔL较大时，窗口距离目标位置较远，会生成较大的核半径。在ΔL较小时，滑动窗口进入目标位置附近，会生成较小的核半径。滑动窗口的半径阈值上限hmax设置为光斑图像尺寸的1/2，滑动窗口的半径阈值下限hmin设置为光源准直光束束腰半径的1/2。

3.3 光斑峰值位置提取算法流程

算法流程图如图3 所示。首先选取图像的中心作为滑动窗口的初始位置。{Ph(k)，Pv(k)}为更新前滑动窗口的位置，{Ph(k+1)，Pv(k+1)}为更新后滑动窗口的位置，k为迭代次数，I为采集到的光斑图像，图像尺寸为m×m。在循环迭代过程中，对滑动窗口范围内的数据，利用式（9）对滑动窗口的位置进行更新：

图3 改进的Meanshift 峰值提取算法流程图Fig.3 Flow chart of the improved Meanshift peak extraction algorithm

每轮迭代完成后，利用式（11）计算滑动窗口的移动量，并代入式（8）对滑动窗口的半径r进行更新：不断执行上述过程，直到滑动窗口的移动量收敛于设定的阈值ε，即满足条件ΔL≤ε。

4 实验与结果

4.1 实验装置

实验装置如图4所示。在光纤激光器（LP642-PF20，642 nm，20 mW，Thorlabs，Newton，NJ，USA）输出端利用准直镜（F810FC-635，NA=0.25，f=35.41 mm）对光束进行准直，出射光束符合束腰半径为3.2 mm的高斯分布。准直光束通过分束镜、1/4 波片（WPQ05ME-633，Ø=1/2"，Thorlabs，Newton，NJ，USA）和显微物镜（LMPLFLN 20×，NA=0.4，f=9 mm，Olympus，Tokyo，Japan）后，汇聚于平面镜（GMH-11，HYGX，Guangzhou，China）表面，平面镜由六轴位移平台（H-811.I2，Power Integrations，San Jose，CA，USA）搭载。反射光重新进入显微物镜后，被分束镜分为两束光束。一束光进入面阵相机（QHY600Pro，9 576×6 388×3.76 μm，光速视觉（北京）有限公司）。另一束光经过平凸透镜（LA1207-A，Ø=1/2"，f=100.0 mm，Thorlabs，Newton，NJ，USA）聚焦后，由分束镜分为焦前测量光束和焦后测量光束，分别射入离焦量为±650 μm 的针孔（SM05PD1B，Ø=20 μm，Thorlabs，Newton，NJ，USA）。增加了辅助成像装置，有助于在设备调校过程中寻找传感器的焦平面。使用的六轴位移台，最小运动增量为2.5 μrad，重复性为±2 μrad，能够满足本实验对倾斜角度的需求。

4.2 实验结果

将待测面调整到不同倾斜角度下，传感器采集到差分共焦曲线如图5 所示。随着倾斜角度的增大，差动响应信号曲线的整体能量也随之降低，进而导致了差动响应信号过零点斜率降低。但是过零点位置不随倾斜角度改变，能够精确定位待测面位置。

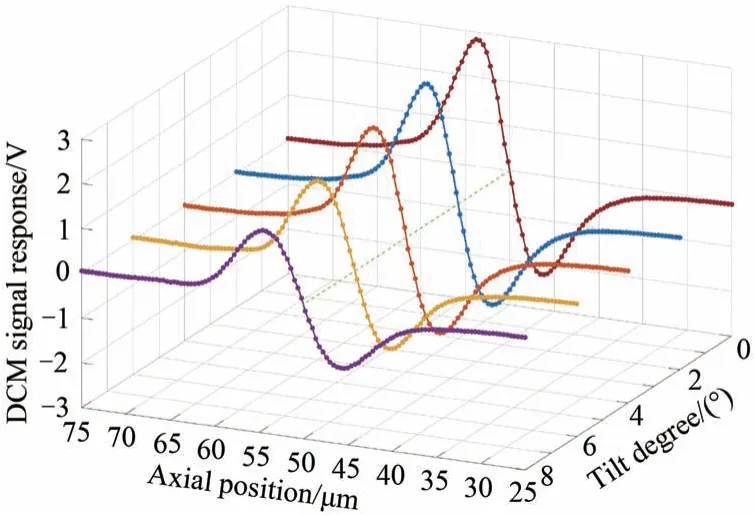
图5 在不同倾斜角度下采集的差动响应信号曲线Fig.5 Differential signal curves collected at different tilt degrees

图6 展示了改进Meanshift算法的峰值提取效果。随着不断的迭代更新，滑动窗口的尺寸开始逐渐缩小，并且越来越接近目标峰值位置。改进的Meanshift 峰值提取算法在初始迭代阶段使用较大的窗口半径，相比于传统的Meanshift 峰值提取算法，使用更少的迭代次数即可锁定峰值位置。

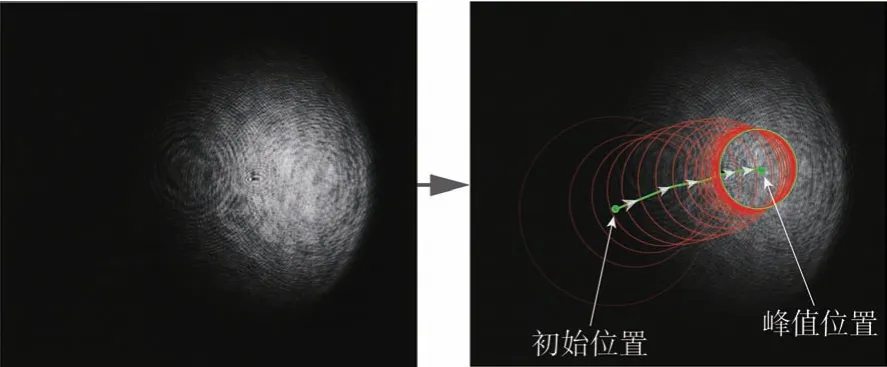
图6 改进Meanshift 算法提取采集的光斑图像峰值位置Fig.6 Peak position of the collected spot image extracted by improved Meanshift algorithm

在对设备的标校实验中，通过六轴位移台将平面镜旋转中心移动到传感器焦点位置，令平面镜围绕传感器焦点位置旋转，产生不同的倾斜角度，面阵相机采集对应的光斑图像。倾斜程度θ范围为0°～+8°，以0.1°为增量，倾斜方向φ范围为0°～360°，以3°为增量，进行训练集数据采集，共采集到19 320 组数据。此外，随机生成4 000 组倾斜角度数据，用于测试集数据采集。图7 和图8 分别展示了采用Biharmonic（v4）曲面插值算法，得到的图像峰值位置与倾斜程度θ以及倾斜方向φ的关系曲面。

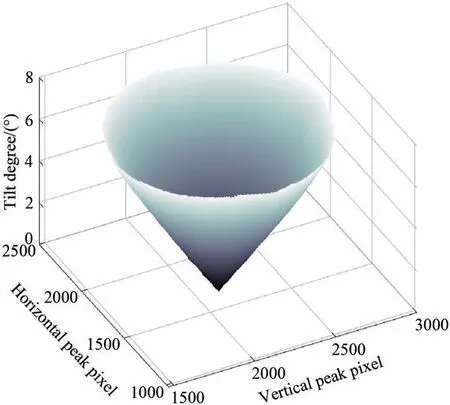
图7 光斑峰值位置与倾斜程度θ 的关系曲面Fig.7 Relationship surface between the peak position of the facula and the tilt degree θ

图9 展示了倾斜程度θ与倾斜方向φ的预测误差随着θ增大的变化情况。随着θ增大，倾斜方向φ的预测误差呈减小的趋势，而倾斜程度θ的预测误差以5°为分界，呈现先减小后增大的趋势。

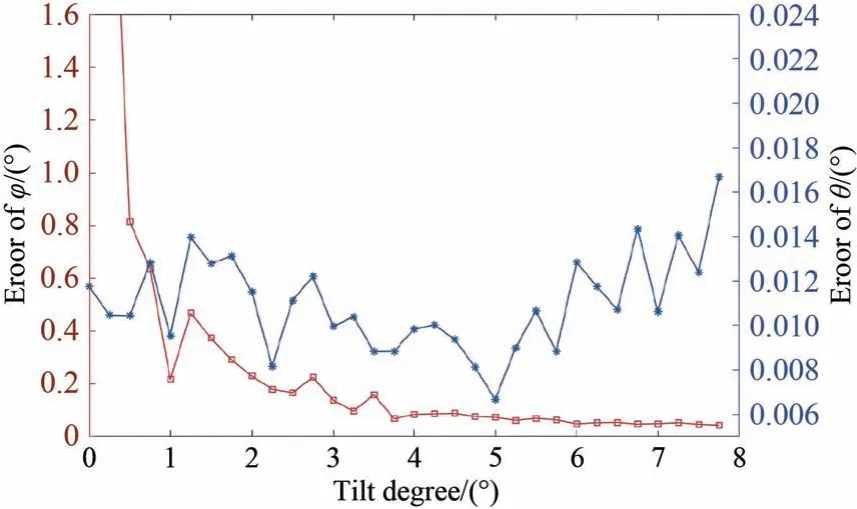
图9 倾斜程度和方向的预测误差随倾斜程度的变化趋势Fig.9 Variation of prediction errors with tilt degree

使用不同的峰值提取算法，对比其测量精度和峰值提取速度。随机生成4 000 组倾斜角度数据作为测试集数据，对其预测误差和平均耗时取加权平均。表1 展示了改进的Meanshift 算法与传统Meanshift、质心法以及二维高斯拟合法的对比结果。实验结果表明，使用改进的Meanshift算法，测量精度能够和传统Meanshift 算法保持一致，速度提升了34%。并且，改进的Meanshift算法相比于质心法预测精度更高，相比于平均预测误差处于同一量级下的二维高斯拟合法，预测速度更快。选用改进Meanshift 算法进行峰值提取，能够兼顾提取的精度与速度。

表1 不同峰值提取算法的测量精度与速度对比Tab.1 Measurement accuracy versus velocity contrast for different peak extraction algorithms

4.3 误差分析

传感器在检测过程中，将提取光斑图像的峰值位置映射为对应的测量倾斜角度。角度测量平均误差对应测量过程中光斑图像峰值误差，约为0.958 个像元。本文对影响所提出传感器测量精度的因素进行了分析，主要包含如下部分：

（1）差分测距单元过零点定位精度

测距单元的焦平面定位误差会影响从显微镜出瞳面出射光束的准直度。差动共焦测距显微镜通过差动响应曲线过零点对焦平面进行精确定位，轴向分辨力能够达到10 nm。对出瞳面光强分布峰值位置进行估计，在倾斜角度为10°时，离焦量10 nm 对应光斑峰值位置的最大偏移量为0.003 6 μm，约0.001 个像元。

（2）标定仪器精度

使用六轴位移平台对本传感器进行标定，标定设备的精确度直接影响了标定的准确性。产生待测面倾斜使用的六轴位移平台，最小倾斜增量为0.000 14°，重复性为±0.000 11°。通过实验验证，本文所提出的传感器的平均测量误差为小数点后两位，传感器的标定以及测试精度需求可以得到保证。

（3）数据处理引入误差

该误差主要是指结合使用算法对图像光斑峰值位置提取的误差。结合仿真分析，改进Meanshift 峰值提取算法对光斑峰值位置的分辨力能够达到0.1 个像元以下。

（4）杂散光以及环境振动引入相机测量误差

由于待测平面不是绝对光滑，相机端探测图像会产生散斑现象。另外，在设备标定以及实际测量过程中，光源的不稳定性、实验环境的振动均会引起光斑图像峰值位置的偏移，这些也是误差产生的主要来源。

5 结 论

本文根据现代光学精密检测中对光学自由曲面表面位置和倾角进行实时同步测量的需求，提出了基于差动共焦的倾角测量结构及其测量方法。建立了倾斜衍射模型，对待测面呈不同倾斜角度时的光斑图像进行了分析。提出了改进Meanshift 峰值提取算法，在保证提取精度的同时，提取速度提升了34%。使用本文提出的传感器以及测量方法，对倾斜程度（0°～8°）的测量平均误差为0.011°，对倾斜方向（0°～360°）的测量平均误差为0.128°。该传感器为传统的差动共焦测距传感器赋予测量倾角的能力，在三维面型精密检测领域有着应用潜力。