图的完全积的独立数和独立多项式
杨利民
(大理大学数学与计算机学院,云南大理 671003)
通过考虑独立多项式根的位置,Brown 等〔1〕证明了每个图是可嵌入作为非常覆盖图的诱导子图,这个图的独立多项式是单峰的。Levit 等〔2〕证明了任何良好覆盖的蜘蛛图的独立多项式都是单峰的。Song 等〔3〕讨论了k-树相关图的独立多项式。目前有许多关于独立多项式的文章讨论单峰性,现在让图论科学家感兴趣的是树的独立多项式的系数成单峰性的猜想。文章列举了独立多项式的系数是单峰的反例,否定了独立多项式的系数是单峰的猜想以及树的独立多项式的系数是单峰的猜想。此外,本文还给出了许多关于图的完全积的独立数和独立多项式的显式公式以及化学图论中许多图的Merrifield-Simmons 指标的显式公式。
1 基本定义和引理
定义1 在图论中,稳定集合(或独立集)是图中的顶点集合,其中没有两个顶点是相邻的。即,它是顶点的集合S 使得对于S 中每两个顶点,没有边联通它们〔4〕。
定义2 图G 中,最大稳定集合的大小叫做图G 的独立数,记为α(G)〔5〕。
定义3 如果sk记图G 中基数为k 的稳定集合的个数,并且α(G)是一个最大稳定集合的大小,那么
叫做图G 的独立多项式〔6〕。
注:容易看出计算独立多项式是NP 难问题。
如果用S(G)记图G 中所有稳定集合的个数,那么
定义4 图的Merrifield-Simmons 指标,记为i(G),由Merrifield-Simmons 提出,它被定义为独立顶点集的总的个数,包括空集〔5〕。
定义5 图G 和H 的完全积,记为GΔH,它是一个新的图,有顶点集V(G)∪V(H)和边集{uv|u∈G,v∈H}∪E(G)∪E(H)〔7〕。

{uv|u∈Gi,v∈Gj,i≠j,1≤i,j≤t}∪E(G1)∪E(G2)∪…∪E(Gt)。
下面是用到的一些基本引理。
引理1 如果sk记图G 中基数为k 的稳定集合的个数,并且ck(G)记补图中阶为k 的完全子图的个数〔8-10〕,那么
证明:假设H(1)=图G 中基数为k 的非空稳定集合的集合,H(2)=补图中阶为k 的完全子图的集合。
映射ϕ 定义如下:
是H 的补图。ϕ 是一个映射。

其中α(G)是补图G 中一个最大完全图的大小。
证明:由定义3、引理1 和引理2,那么就有
其中α(G)是补图G 中一个最大完全图的大小。
引理4 存在计算恒等式如下:
2 主要结论
以下将研究图的完全积的独立数和独立多项式以及独立多项式系数的单峰性。
定理1 如果G 是图G1,G2,…,Gn的完全积,那么
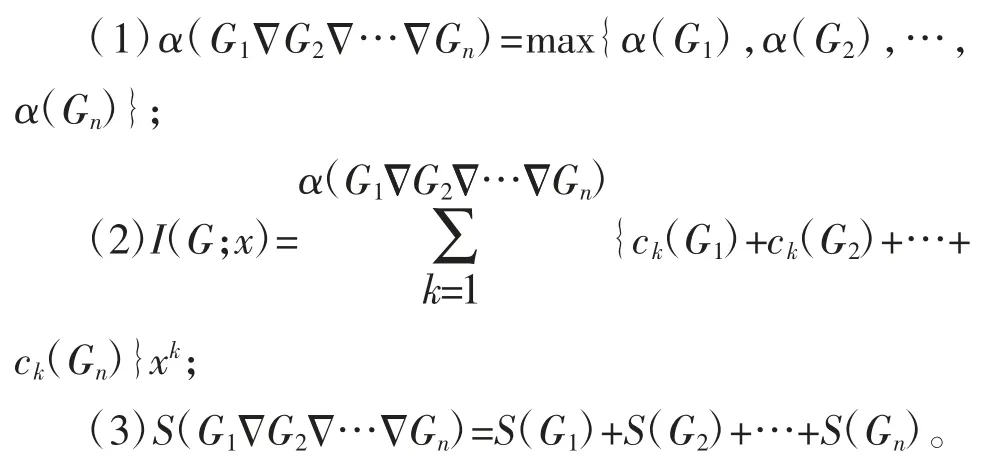

再根据引理3,于是

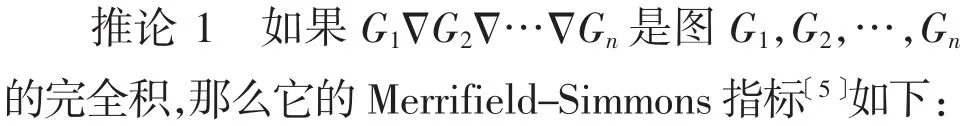
证明:文献〔5〕给出了上述等式的归纳法证明,但是不好理解。在这里给出它的第二种简洁证明。证明如下:
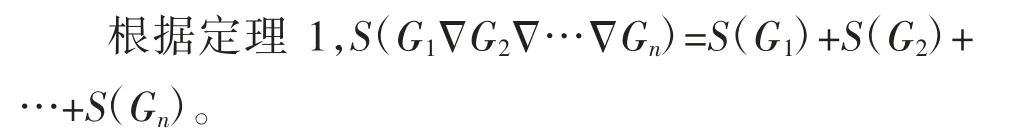
由于引理4,i(G)=S(G)+1,所以S(G)=i(G)-1。于是
再根据引理4,所以就有
一个风车图是它的边被划分成完全图的边的集合,这些完全图有且仅有一个公共点,即,图G 有(n1+n2+…+nd)-d+1 个顶点,G=Kn1∪Kn2∪…∪Knd,并且Kn1∩Kn2∩…∩Knd=K1,那么G 叫做一个风车图。
特别地,n∈N,令n1=n2=…=nd=n,风车图记为Knd。

(2)由于ck(G)= 在K1和Kn-1,n-1,…,n-1中阶为k的完全子图的个数,于是〔11-13〕
所以,根据引理3 得到风车图的独立多项式如下:
通过引理4 得到风车图的Merrifield-Simmons指标如下:
推论2 如果G 是一个风车图,那么它的独立多项式的系数序列不是单峰的。
证明:下面举个反例,令G=K1210,其中n=12,d=10。根据定理2 的证明过程得到如下的系数:

通过定理1 和定理2,可得
根据定理1,于是
定理4 如果G 是一个(n-2)-度正则图,且顶点个数为n(偶2m),那么(1)α(G)=2;(2)I(G;x)=2mx+mx2;(3)i(G)=3m+1。

通过引理3,于是I(G;x)=2mx+mx2。
(3)根据上述证明过程得到I(G;x)=2mx+mx2,于是I(G;1)=2m×1+m×12=3m。再根据引理4,i(G)=I(G;1)+1,所以有i(G)=3m+1。
推论3 如果G 是一个(n-2)-度正则图,且顶点个数为n(偶2m),那么它的独立多项式的系数序列不是单峰的。
证明:根据定理4,I(G;x)=2mx+mx2,它的系数序列为:2m,m。
结论:不是单峰的。
定理5 如果G 是(n1-2)-度正则图,(n2-2)-度正则图,…,(nq-2)-度正则图的完全积,nj是(2mj),1≤j≤q,那么
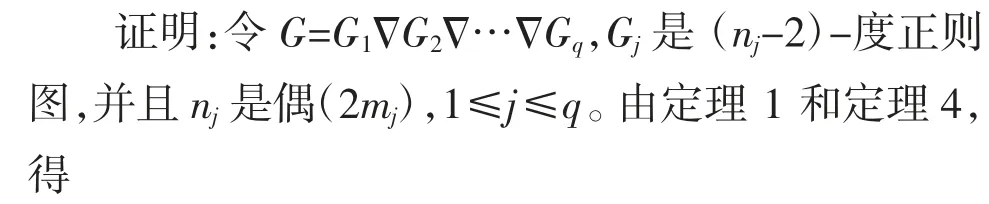
根据定理1,那么
根据上述的独立多项式,I(G;1)=3(m1+m2+…+mq)。通过引理4,i(G)=I(G;1)+1,所以,i(G)=3(m1+m2+…+mq)+1。
定理6 假设G 是一个完全q-部图Kn1,n2,…,nq那么
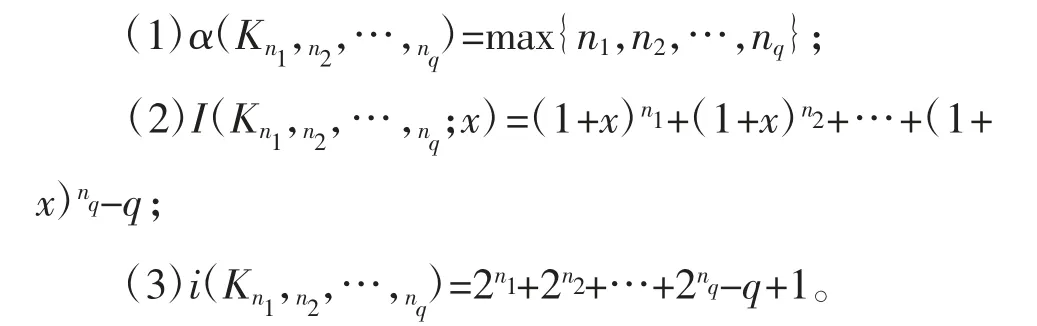

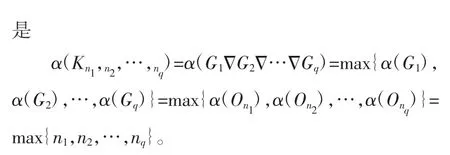
(2)由于
通过定理1 ,所以,
(3)根据上述结论,
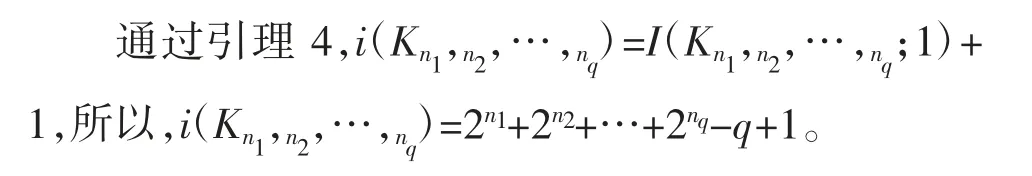
推论4 假设G 是一个完全q-部图Kn,n,…,n,那么
(1)α(Kn,n,…,n)=n;
(2)I(Kn,n,…,n;x)=q(1+x)n-q;
(3)i(Kn,n,…,n)=q2n-q+1。
证明:(1)来自定理6,令n1=n2=…=nd=n,α(Kn,n,…,n)=max{n,n,…,n}=n。
(2)来自定理6 的证明过程,于是
(3)根据上述发生函数,于是I(Kn,n,…,n;1)=q(1+1)n-q=q2n-q,并且通过引理4,i(Kn,n,…,n)=I(Kn,n,…,n;1)+1,所以i(Kn,n,…,n)=q2n-q+1。
推论5 Kn,n,…,n的独立多项式的系数序列是单峰的。
证明:来自推论4 的证明过程,Kn,n,…,n的独立多项式的系数序列构成如下:
结论:序列是单峰的。
定理7 如果G 是星形图K1,n1,K1,n2,…,K1,nq的完全积,那么
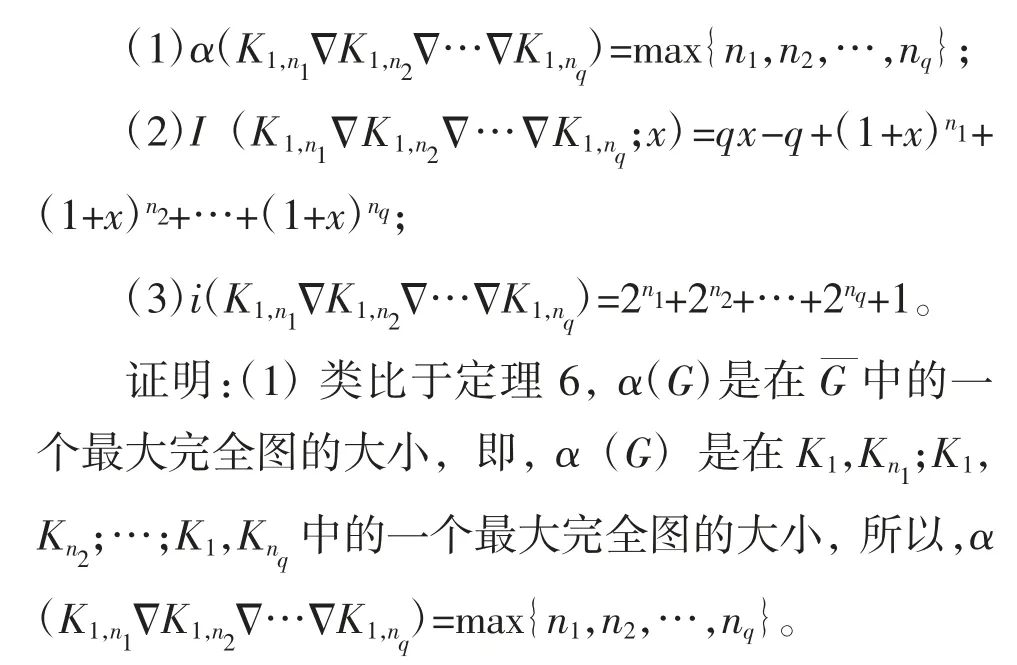
(2)通过定理1,于是
(3)根据上述发生函数,得到

根据定理1,那么

结论:当n≥4,它的系数序列是单峰的。
推论8 假设G 是图K1,3,K1,3,…,K1,3的完全积,那么

结论:它的系数序列不是单峰的。
特别地,K1,3是一棵特殊的树,I(K1,3;x)=4x+3x2+x3,它的系数序列不是单峰的,所以,树的独立多项式的系数序列不是单峰的〔14〕。这样就否定了树的独立多项式的系数是单峰的猜想。
综上所述,独立多项式的系数序列的单峰性猜想被否定。
本文中,通过转化问题,从一般到特殊和类比三大主要的数学思想,进一步获得图的完全积的独立数和独立多项式和技巧性地计算Merrifield-Simmons 指标,同时否定了树的独立多项式的系数序列是单峰的猜想。

