矩阵乘积AB与BA的相似问题
杨 涌, 戴星宇, 李 俊
(国防科技大学 理学院,长沙 410073)
0 引 言
线性代数中Jordan标准形的构造有多种方法,本文给出基于广义特征向量的构造方法.本方法的好处是可以明确的体现Jordan标准形的构造与空间的广义特征子空间分解等价.
基于这种方法,本文进一步分析了矩阵乘积AB与BA的特征子空间的关系,进而得到定理1:若矩阵A∈m×n,B∈n×m,则AB与BA的Jordan标准形中对应非零特征值有完全相同的Jordan块.
进一步由定理1给出了矩阵乘积AB与BA相似的充分必要条件,即推论3:若方阵A∈n×n,B∈n×n, 则AB与BA相似的充分必要条件是对任意正整数r∈+,
rank(AB)r=rank(BA)r.
1 广义特征子空间和Jordan标准形构造
对于任意方阵A来说,其可对角化的一个重要条件就是其特征向量可以组成整个空间n的一组基.但是,对于一般的方阵,其特征向量不足以组成空间n的一组基.为此,考虑在特征向量集(空间)上再加入一些向量,例如广义特征向量集(空间)((A-λE)nx=0的解空间).这样就需要考察两个问题:(i) 扩充后的向量集能否构成全空间的一组基;(ii)在新的基下矩阵会相似于什么形态.
对于第一个问题可利用线性代数中的结论:“属于不同特征值的特征向量线性无关”的推广形式,即引理1和引理2给予解答.
为了考虑第二个问题,通过进一步分解广义特征向量集(空间),从而得到一般矩阵在相似变换下的一个较为简单的形式:Jordan标准形.
1.1 广义特征子空间及空间n的分解
引理1设A是n阶方阵,多项式f(λ),g(λ)互素,并令Vf,Vg,Vfg分别为方程组f(A)x=0,g(A)x=0与方程组f(A)g(A)x=0的解空间,则对任意向量η∈Vfg,存在向量α∈Vf,β∈Vg,使得η=α+β.
证由f(λ),g(λ)互素,存在多项式p(λ)和q(λ)满足f(λ)p(λ)+g(λ)q(λ)=1,于是有
f(A)p(A)+g(A)q(A)=E,
设η∈Vfg,即f(A)g(A)η=0,则有
f(A)p(A)η+g(A)q(A)η=η,
注意到f(A)p(A)η=β∈Vg,g(A)q(A)η=α∈Vf,引理得证.
引理2设A是n阶方阵,多项式f(λ),g(λ)互素,并令Vf,Vg分别为方程组f(A)x=0与方程组g(A)x=0的解空间,则任意非零向量α∈Vf,β∈Vg线性无关.
证由f(λ),g(λ)互素,存在多项式p(λ)和q(λ)满足f(λ)p(λ)+g(λ)q(λ)=1,于是有
f(A)p(A)+g(A)q(A)=E.
假设命题不真,即存在α∈Vf,β∈Vg线性相关,则存在不全为零的系数λ和γ满足λα+γβ=0.不妨设γ≠0,于是有
0=f(A)λα+f(A)γβ=f(A)γβ,
从而有f(A)β=0,即β∈Vf∩Vg.
又由f(A)p(A)+g(A)q(A)=E,得
β=Eβ=f(A)p(A)β+g(A)q(A)β=0,
这与条件β≠0矛盾.于是假设不真,引理得证.
利用以上引理可得以下结论.

(A-λ1E)n1x=0,(A-λ2E)n2x=0,…,(A-λsE)nsx=0
{αλ11,αλ12,…,αλ1d1},{αλ21,αλ22,…,αλ2d2},…,{αλs1,αλs2,…,αλsds},
则{αλ11,αλ12,…,αλ1d1,αλ21,αλ22,…,αλ2d2,…,αλs1,αλs2,…,αλsds}构成向量空间n的一组基.即空间n有直和分解

通过以上的结论,给定方阵A,可以将空间n分解为A的广义特征子空间的直和.实际上,还可以进一步对广义特征子空间进行分解,从而给出一组更简洁的基,在这组基下矩阵A相似于其Jordan标准形.


在向量组
{(A-λiE)ni-1αλi1,(A-λiE)ni-1αλi2,…,(A-λiE)ni-1αλidi}
中取极大线性无关组(若以上向量组全为零,则在倒数第二行组成的向量组中找极大线性无关组,以此类推),不妨设为
{(A-λiE)ni-1αλi1,(A-λiE)ni-1αλi2,…,(A-λiE)ni-1αλiri},
则有
(i) 向量组
线性无关.
Step 2: 注意到向量组

分别左乘方阵(A-λiE)ni-k,2≤k 在向量组 中将线性无关组 {(A-λiE)ni-1αλi1,(A-λiE)ni-1αλi2,…,(A-λiE)ni-1αλiri} 扩充成一个极大无关组,不妨设为 {(A-λiE)ni-1αλi1,…,(A-λiE)ni-1αλiri,(A-λiE)ni-2βri+1,…,(A-λiE)ni-2βri+li}, 则有向量组 线性无关; 进一步,通过上面一组基的构造法不难得出如下的结论(该结论也可见文献[1]中定理2). 推论2设n阶方阵A有特征值λ, 则A的Jordan标准形中对角线元素为λ且阶数大于等于r的Jordan块的个数为 rank(A-λE)r-1-rank(A-λE)r. 进一步,则A的Jordan标准形中对角线元素为λ且阶数等于r的Jordan块的个数为 rank(A-λE)r-1+rank(A-λE)r+1-2rank(A-λE)r. 本节首先利用前面得到的结论证明如下的定理. 定理1若矩阵A∈m×n,B∈n×m, 则方阵AB与BA有完全相同的非零特征值,并且对应任意相同的非零特征值,在AB与BA的Jordan标准形中有完全相同的Jordan块. 证首先证明AB与BA有完全相同的非零特征值.设λ是AB的任一非零特征值,则存在非零向量α,使得ABα=λα,进而BABα=λBα.由于ABα=λα≠0,从而Bα≠0.于是λ也是BA的非零特征值.同理也可以证明,BA的任意非零特征值也是AB的非零特征值,从而定理的第一部分得证. 下面证明定理的第二部分.设λ是AB(同时也是BA)的特征值.根据推论2只需证明对任意正整数r,都有 rank(AB-λEm)r-rank(AB-λEm)r+1=rank(BA-λEn)r-rank(BA-λEn)r+1 即可. 为此,只需证明广义特征子空间V1与广义特征子空间V2有相同的维数,也就是方程组 (AB-λEm)rx=0与(BA-λEn)ry=0 的解空间有相同的维数,即dimV1=dimV2. 设α∈V1,则(AB-λEm)rα=0,从而有 B(AB-λEm)rα=(BA-λEn)rBα=0, 即Bα∈V2,于是矩阵B定义了线性变换B:V1→V2. 若0≠α∈V1,则由(AB-λEm)rα=0可知 若Bα=0,则上式左边等于零,而λ≠0,α≠0,故等式右边不为零,矛盾!因此对任意0≠α∈V1,总有Bα≠0,从而映射B:V1→V2是单射,即dimV1≤dimV2.同理也可证明dimV2≤dimV1,从而定理得证. 注 由定理1可知,方阵AB与BA在非零特征值部分是相似的. 推论3若方阵A∈n×n,B∈n×n, 则AB与BA相似的充分必要条件是对任意正整数r∈+,rank(AB)r=rank(BA)r. 证根据推论2,由定理1的证明过程可知AB与BA相似当且仅当对任意r∈+,及任意特征值λ,方程组 (AB-λEn)rx=0与(BA-λEn)ry=0 的解空间有相同的维数. 对于非零的特征值λ,根据定理1可知结论恒成立,因此只需考虑零特征值的情况.注意到此时AB与BA都是n阶方阵,因此方程组 (AB)rx=0与(BA)ry=0 解空间维数相同,当且仅当rank(AB)r=rank(BA)r,推论得证. 推论4设方阵A∈n×n,B∈n×n,则方阵(AB)n与(BA)n相似. 证根据定理1,AB与BA的Jordan标准形中对应非零特征值的Jordan块完全相同.于是不妨设AB与BA的Jordan标准形分别为 其中Jλ≠0表示由非零特征值对应的Jordan块构成的准对角阵,J0与J′0表示由特征值0对应的Jordan块构成的准对角阵.于是(AB)n与(BA)n分别相似于 推论5(希尔维斯特定理) 设矩阵A∈m×n,B∈n×m,则下列等式成立 λn|λEm-AB|=λm|λEn-BA|. 证注意到方阵AB与BA的Jordan标准形中对应非零特征值的Jordan块完全相同.因此特征多项式|λEm-AB|与|λEn-BA|的非零根一一对应,分别乘λn与λm后得到次数相等的首一多项式λn|λEm-AB|与λm|λEn-BA|,且它们的根一一对应,于是相等. 本文给出利用线性空间的广义特征特征子空间分解构造矩阵的Jordan标准形的方法.该方法揭示出线性空间的(不变子空间)分解与多项式分解,以及线性变换的分解的内在联系.特别地,空间的分解可以给出矩阵的对应分解.通过对相应的空间分解的分析和计算,文章给出了矩阵乘积AB与BA相似当且仅当rank(AB)r=rank(BA)r,任意r∈+,以及希尔维斯特定理的一个推广形式. 致谢本文作者对国防科技大学数学系周悦研究员、宋伊萍副教授关于本文部分内容的有益讨论表示感谢.
2 矩阵乘积AB与BA的相似问题
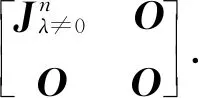
3 结 论

