二维曲线型随机变量函数的概率分布
涂振坤, 贾兆丽2,, 宁荣健
(1.合肥工业大学 数学学院,合肥 230601; 2.新疆农业大学 数理学院,乌鲁木齐 830052)
0 引 言
文献[1]中提出,如果二维随机变量(X,Y)只在平面曲线L上取值,就称(X,Y)为在曲线L上取值的二维曲线型随机变量.
在文献[2]中,给出了下面的结论.
引理1[2]设二维随机变量(X,Y)在区域D内(上)取值,其密度函数为f(x,y),且当(x,y)∈D时,f(x,y)>0.L为D内的一条光滑曲线,其方程为h(x,y)=0,且h′x(x,y)和h′y(x,y)均连续,h′y(x,y)≠0.记u=x,v=h(x,y),y=H(u,v),则
本文将对上述结论再作进一步挖掘,探讨当二维曲线型随机变量(X,Y)∈L时,U=g(X,Y)的概率分布问题.
1 主要结论
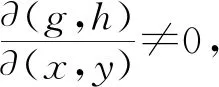
(1)
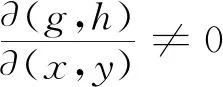
由此得V的密度函数为
考虑到(u,v)∈Duv时,fUV(u,v)>0,故
又(X,Y)∈L等价于V=0,由条件密度函数定义有
推论1设a (2) 在(2)中令b=u,a=-∞,可得当(X,Y)∈L时,U=g(X,Y)的分布函数为 如果在定理1及推论1中分别取u=g(x,y)=x和u=g(x,y)=y,则可得 (3) 进而有 (4) (5) 进而有 (6) 不难发现,式(4)就是引理1中的结论,可见引理1是推论1的特例. 如果定理1中的变换u=g(x,y),v=h(x,y)不是一一对应的,则定理1的结论就不成立. 因此需要将定理1作进一步拓展.为此给出文献[4]中的如下结论. 则(U,V)的密度函数为 则当(X,Y)∈L时,U=g(X,Y)的密度函数为 (7) 证由引理2 故 得 例1设二维随机变量(X,Y)的密度函数 L:x2+y2=1,U=X-Y. (i) 分别求U的密度函数fU(u),P{U≥0}以及边缘密度函数fX(x),fY(y); (ii) 当(X,Y)∈L时,分别求U的密度函数fU|(X,Y)(u|L),P{U≥0|(X,Y)∈L}以及条件密度函数fX|(X,Y)(x|L),fY|(X,Y)(y|L). 解(i) ① 由(X,Y)的密度函数为f(x,y),知 当u<-1时,FU(u)=0;当u≥1时,FU(u)=1; 故 (ii) ① 由题意 L:x2+y2=1,0 由式(3)得 由式(5)得 本例(i)中,fU(u),P{U≥0}以及fX(x),fY(y)反映的是作为在矩形区域0 例2设二维随机变量(X,Y)的密度函数为 其中D:-1 由于当v=0时,0 本例中,由于变换u=x2,v=y-x2在D内并非一一对应,因此需将D分为D1和D2两个部分,再利用定理2进行求解,可见定理2使得求二维曲线型随机变量函数的密度函数的方法变得更加丰富,适用范围更广. 由于在实际问题中存在曲线型随机变量的现象,因此研究曲线型随机变量具有一定的理论价值和应用价值.但目前有关曲线型随机变量的研究还不是很多,本文是在文献[2]的基础上作了一定的引伸或拓展,将曲线型随机变量的概率计算问题提升到曲线型随机变量函数的概率分布问题,抛砖引玉,努力丰富和完善曲线型随机变量的理论. 本文主要的工作是定理1和定理2.在定理1中给出了当(X,Y)∈L时,(X,Y)的函数U=g(X,Y)的密度函数fU|(X,Y)(u|L)的计算公式.并由此相应地得到当(X,Y)∈L时,P{a≤U≤b|(X,Y)∈L},以及密度函数fX|(X,Y)(x|L)和fY|(X,Y)(y|L)等的计算方法.定理2是定理1的引伸,适用范围更广. 致谢感谢审稿人给出的宝贵意见,感谢唐烁老师对论文的内容及结构等方面的指导.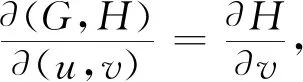
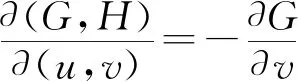
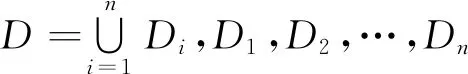
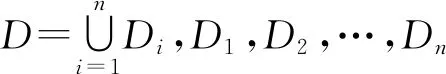
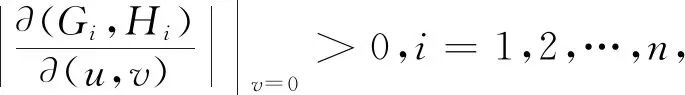
2 应用算例
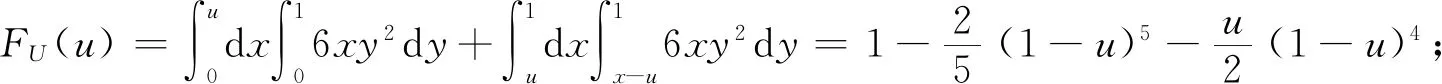
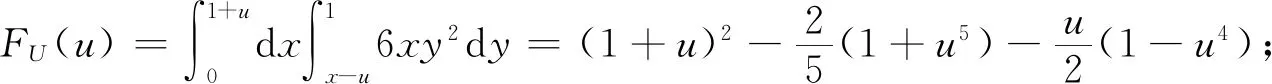
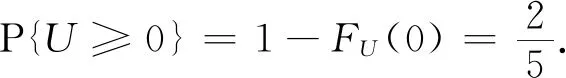
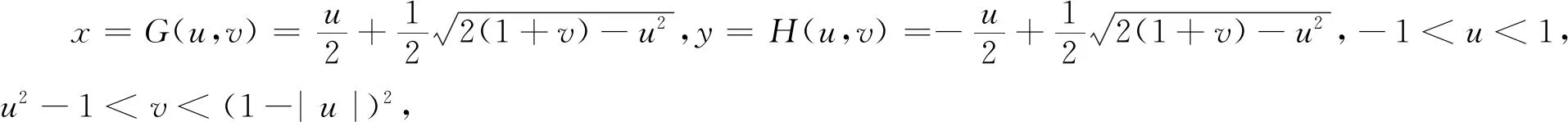
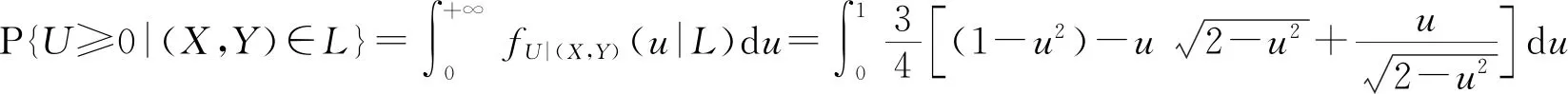
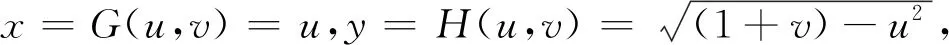
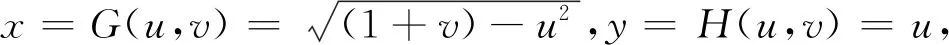
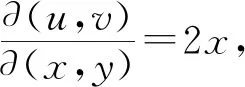
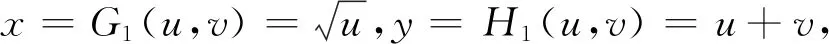
3 结 论

