“1”的加减乘除
☉湖北省枣阳市第一中学 陈刚明
“1”在高中数学的不同章节中有着不同的等量代换形式,灵活使用“1”的加减乘除运算能够使高中数学中的相关运算达到“柳暗花明又一村”的效果.现举例说明:
一、“1”的加法
例1计算的值.
解:原式
例2求的值.
解:
以上两个例子均采用的方法是在所求式子的首项前加“1”,配凑后使用相关性质进行计算.
二、“1”的减法
例3(2013年新课标全国2理)设a=log36,b=log510,c=log714,则( ).

解析:本例中要比较的三个数都形如“loga2a”,由对数函数的性质loga2a=loga2+logaa=loga2+1可知,把每个数都减去“1”,还得“庐山真面目”,即a=log36=1+log32,b=log510=1+log52,c=log714=1+log72,则只要比较log32,log52,log72的大小即可.在同一直角坐标系下作出函数图像,由三个函数图像的相对位置关系,可知a>b>c,故选D.
例4在数列{an}中,当n≥2,n∈N*时,an=2an-1-1,且a1=2,求数列{an}的通项公式.
解:由an=2an-1-1可得,an-1=2(an-1-1),
所以{an-1}构成以a1-1为首项,2为公比的等比数列.
所以an-1=1·2n-1=2n-1.
所以an=2n-1+1.
点评:本例中在原等式的两边同时减去“1”,把递推数列化归为等比数列,进而求出数列{an}的通项公式.
三、“1”的乘法
例5已知x,y>0且x+2y=1,求的最小值.
解:因为x+2y=1,
例6已知f(x)是定义在[-1,1]上的奇函数,若m,n∈[-1,1],m+n≠0时,有,证明:(fx)在[-1,1]上是增函数.
证明:任取-1≤x1<x2≤1,则
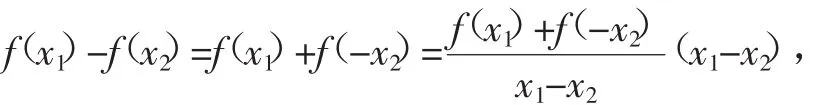
因为-1≤x1<x2≤1,所以x1+x2≠0.
所以f(x)在[-1,1]上是增函数.
例7求函数的值域.
解:函数的定义域为[0,+∞),

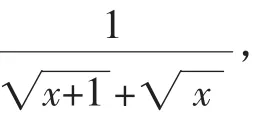
四、“1”的除法
例8已知tanα=2,求sinαcosα+sin2α的值.
解 :
点评:本例中把sinαcosα+sin2α除以sin2α+cos2α=1转化为齐次式,分子分母再同时除以cos2α,使得问题得解.
例9函数f(x)的图像如图1所示,下列数值排序正确的是( ).

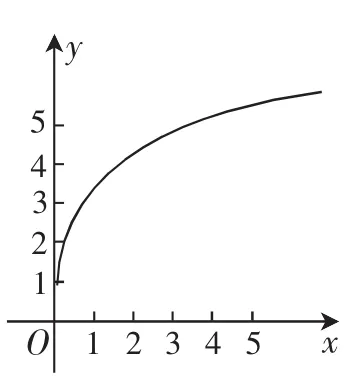
图1
解:f′(2),f′(3)分别是x为2,3时图像上对应点处的切线斜率,因为,所以(f3)-(f2)是图像上x分别为2和3时所对应的两点连线的斜率,故选B.
点评:本例中把f(3)-f(2)除以3-2=1,使得f(3)-f(2)具有明确的几何意义(两点连线的斜率),然后从几何图象就可以判断出它们的大小关系.

