人教A版新旧教材关于“空间向量与立体几何”的比较研究

王梁静 杨红萍

摘 要：本文通过对新旧课标“空间向量与立体几何”内容要求比较分析，发现新课标的内容划分及内容要求都更为具体.在此基础上对新旧教材“空间向量与立体几何”的章节编排、知识点增减、例习题配置三个方面比较分析，发现新教材更注重知识的系统性和逻辑性，更注重思想方法及核心素养的渗透，且新教材知识点和例习题数量均多于旧教材，新教材例习题难度高于旧教材.最后提出关注数学思想方法的渗透和核心素养的培养、加强立体几何中向量方法的教学等教学建议.

关键词：新旧教材；空间向量与立体几何；比较研究

1 研究背景

2023年5月29日，习近平总书记在中共中央政治局第五次集体学习时指出，我们建设教育强国的目的，就是培养一代又一代德智体美劳全面发展的社会主义建设者和接班人，培养一代又一代在社会主义现代化建设中可堪大用、能担重任的栋梁之材，确保党的事业和社会主义现代化强国建设后继有人.在学校教育中，教材具有非常重要的地位.从学生学的角度看，教材具有兴趣激发和活动指导、学科展示和内外衔接等功能；从教师教的角度看，教材具有教学依据、资源提供等功能^［1］.

“空间向量和立体几何”是数学教材中的一个重要部分，在数学学科中具有重要的地位.它为学生提供了一种解决几何问题的方法和工具，可培养学生思维能力，激发学生对数学的兴趣和创造力等.此外，“空间向量和立体几何”在生活中有着广泛的应用，涉及到导航、交通规划、航空航天等领域，对整个社会和经济发展起着重要的促进作用.

本文選取人教A版《普通高中课程标准实验教科书数学选修2-1》（2007年2月）（以下简称“旧教材”）和《普通高中教科书数学选择性必修第一册》（2020年5月）（以下简称“新教材”）中的“空间向量与立体几何”进行比较.两版教材编写所依据的课程标准分别是《普通高中数学课程标准（实验）》（以下简称“旧课标”）和《普通高中数学课程标准（2017年版）》（以下简称“新课标”）（注：《普通高中数学课程标准（2017年版2020年修订）》中这部分内容没有变化，故本文采用《普通高中数学课程标准（2017年版）》）.下面对新旧课标“空间向量与立体几何”的内容要求比较分析，对新旧教材“空间向量与立体几何”的章节编排、知识点增减及例习题配置等比较分析，揭示两版教材之间的差异，并给出相关教学建议.

2 新旧课标“空间向量与立体几何”的内容要求比较

课程标准是教材编写、教师进行教学的直接依据.相较于旧课标，新课标在每个主题“内容要求”基础上增加了“教学提示”和“学业要求”，而“内容要求”表明了“学什么”.下面以新课标为基准，对比分析新旧课标“空间向量与立体几何”的内容要求.

2.1 新课标内容划分更具体

通过比较发现，旧课标“空间向量与立体几何”中包括两个内容，分别是“空间向量及其运算”及“空间向量的应用”.而新课标中包括四个内容，分别是“空间直角坐标系”“空间向量及其运算”“向量基本定理及坐标表示”及“空间向量的应用”.

内容模块主要有两个方面的变化：第一，新课标将“空间直角坐标系”纳入“空间向量与立体几何”，而旧课标“空间直角坐标系”位于“平面解析几何初步”.第二，新课标将旧课标中“空间向量及其运算”这一内容拆分为“空间向量及其运算”和“向量基本定理及坐标表示”两个内容.这些变化使知识衔接更加合理，增强了前后知识的联系；且内容划分更加具体，突出了其系统性.

2.2 新课标内容要求更具体

相较于旧课标，新课标增加了“了解空间向量投影的概念以及投影向量的意义”“能用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的平面的距离问题”两个内容要求，且关于“空间向量的应用”内容要求描述更加具体.第一，空间向量投影概念的建立对于学生利用投影向量研究立体几何有重要意义.第二，新课标中突出了向量法和坐标法解决立体几何问题的重要作用，有利于培养学生的数学建模、直观想象和数学运算等素养.

3 新旧教材“空间向量与立体几何”的内容比较

在比较分析新旧课标的基础上，对新旧教材“空间向量与立体几何”的章节编排、知识点增减、例习题配置三个方面比较分析，为一线教师运用新教材及落实新课标基本理念提供参考.

3.1 章节编排比较

新旧教材的章节编排顺序以课程标准为依据，反映课标所侧重的知识结构与学科知识之间的内在逻辑.教材章节的编排顺序要符合本学科的内在联系，符合学生的认知发展规律.新旧教材章节编排顺序有一定的差异，详见表3-1.

3.1.1 新教材更注重知识的系统性

章建跃（2019）指出教材体系要体现顺序性、连续性，新教材的结构体系关注了整体性^{［2］［3］}.通过比较发现，新教材中“空间直角坐标系”位于选择性必修第一册第一章“空间向量与立体几何”，而在旧教材中位于必修2第四章“圆与方程”.新教材将此编排，为研究直线、平面的位置关系及研究距离、夹角问题奠定基础.建立了前后知识的联系，突出了“空间向量与立体几何”章节的整体性和系统性，符合学生的认知发展规律.因此，新教材更注重知识的系统性.

3.1.2 新教材更注重知识的逻辑性

新教材打破了原教材的模块化结构和螺旋式上升安排，使内容的逻辑顺序更加合理^［4］.邵光华（2019）指出新教材调整了章节内容结构，凸显了知识间联系^［5］.旧教材“空间向量与立体几何”共两节内容，而新教材共四节内容，且标题明确，逻辑性强.具体体现在以下三点：

第一，新教材将“空间向量基本定理”单独成节，而旧教材中该内容位于“空间向量及其运算”中一节，且小标题为“空间向量的正交分解及其坐标表示”.由此可以看出，新教材突出了“空间向量基本定理”的重要性，它是立体几何问题代数化的基础，为后两节内容奠定基础.第二，新教材将“空间直角坐标系”纳入“空间向量与立体几何”这一章，使前后知识形成一个整体，建立了紧密的联系.第三，新教材“空间向量的应用”这一节中，将“用空间向量研究直线、平面的位置关系”“用空间向量研究距离、夹角问题”作为标题呈现，突出了立体几何中向量法的重要性.综合以上，新教材中知识的逻辑性更强.

3.1.3 新旧教材均注重数学阅读

新旧教材都包含阅读与思考栏目，其内容都为向量概念的推广与应用.两版教材均通过实际问题表示了几何向量，并推广到n维向量.此外，两版教材通过两个实例阐述向量的加法与数乘运算、用“距离”解决实际问题.由此可以看出，尽管新旧教材所列举的例子不同，但阅读与思考栏目均占了很大篇幅，故新旧教材均注重数学阅读.

3.1.4 新教材中的情境更贴近实际生活

新旧教材在阅读与思考栏目，都介绍了向量概念的应用，但“用‘距离解决实际问题”所举的例子不同.旧教材是通过计算由燕隼与红隼体型数据构成的向量与标准点的距离，进而判断此类鸟的分类；而新教材是通过计算由校服尺寸所构成的向量与标准点的距离，进而判断校服尺码的分类.由此可以看出，新教材中的情境更加贴近学生的实际生活.

3.2 知识点增减比较

数学教材知识点的选取不仅要突出本章的重要内容，还要体现数学思想方法和核心素养的渗透.为了保障划分知识点时减少误差，以教材中用特殊标记标注的概念与命题作为知识点，对新旧教材“空间向量与立体几何”所含知识点进行梳理，如表3-2所示.

3.2.1 新教材的知识点多于旧教材

从表3-2中可以发现，新教材增加了5个知识点，分别是“单位正交基底”“空间中点、直线和平面的向量表示”、证明“直线与平面平行的判定定理”、证明“平面与平面垂直的判定定理”及“用空間向量研究距离和夹角问题”.尽管旧教材中涉及了用空间向量研究夹角问题，但并没有采用特殊标记标注.

3.2.2 新教材更凸显数学思想方法

章建跃（2019）指出“教材特别注意以数学核心概念及其反映的数学思想方法为纽带建立内容之间的联系，提高学生数学思维能力，培育理性精神^［3］.”从表3-2中可以看出，新教材增加了“单位正交基底”，体现了特殊与一般的思想方法，知道单位正交基底是特殊的向量基底；增加了“用空间向量研究距离和夹角问题”，体现了化归与转化的思想方法，将空间直线与直线、直线与平面、平面与平面的距离、角度等问题转化为以直线的方向向量和平面的法向量为基础的向量问题.故从知识点的增加情况来看，新教材更凸显数学思想方法.

3.2.3 新教材更注重数学核心素养

数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现^［6］.新教材增加了“用空间向量研究距离和夹角问题”，而距离和角度是立体几何中的基本度量.通过求解距离和角度问题，可以帮助学生归纳用空间向量解决立体几何问题的“三步曲”，并用其解决立体几何问题，从而培养学生直观想象、数学运算和逻辑推理等数学学科核心素养.

3.3 例习题配置比较

数学学习的过程中，除了需要理解知识点之外，还需做相应的例习题巩固知识点，以达到对知识的掌握.数学教材中例题具有示范引领、揭示方法、文化育人等功能^［7］.习题具有巩固消化新知、综合运用新知、思想方法渗透等功能^［8］.

3.3.1 例习题数量比较

若某题目包含多个小问，则按一题计；若选择题（或判断题，或填空题）包含多个小题（或多个空），则按一题计.由于新旧教材“空间向量与立体几何”章节编排不同，为方便统计，将其分为“空间向量基础知识”和“空间向量的应用”两个板块.

通过统计比较发现，新教材例习题数量多于旧教材.其中新教材例习题共124道，旧教材共92道，新教材比旧教材多32道题目.对于例题数量，“空间向量的应用”这一内容新旧教材相差较大，新教材多6道题目；对于习题数量，“空间向量基础知识”这一内容新教材多9道题目，“空间向量的应用”这一内容新教材多15道题目；对于复习参考题数量，新旧教材相差不大.

3.3.2 例习题题型比较

通过观察新旧教材例习题发现，其题型主要有选择题、填空题、判断题、解答题和证明题.若一道题目中有多个小题，其中既有解答题又有证明题，则分开计；若都为解答题或都为证明题，则按一题计.若选择题（或判断题，或填空题）中有多个小题（或多个空），则按一题计.

（1） 新教材例习题题型多于旧教材

通过比较发现，旧教材中没有填空题和判断题，而新教材中增加了这两个类型的题目，且都位于“空间向量的应用”这一节.填空题考查的是在棱长为1的正方体中，点、直线、平面分别到平面的距离，即考查运用空间向量及其运算研究距离问题.通过前面的例题，学生学习了用空间向量解决具体的立体几何问题.之后在练习题中给出该填空题，题目较简单，考虑到了不同能力学生的需求，且为后两道题目奠定基础.判断题考查直线的方向向量和平面的法向量相关知识，该题目的设置可加深学生对方向向量和法向量的理解，为后续的学习进一步打下基础.

（2） 新教材各题型的题目数量均多于旧教材

通过比较发现，新教材每一种题型的数量均多于旧教材，集中体现在解答题和证明题中.新教材解答题和证明题比旧教材均多16道.通过巩固练习，学生掌握本章的核心知识，把握知识之间的内在联系，同时促进学生空间观念的养成，考查其理性思维能力.

3.3.3 例习题难度比较

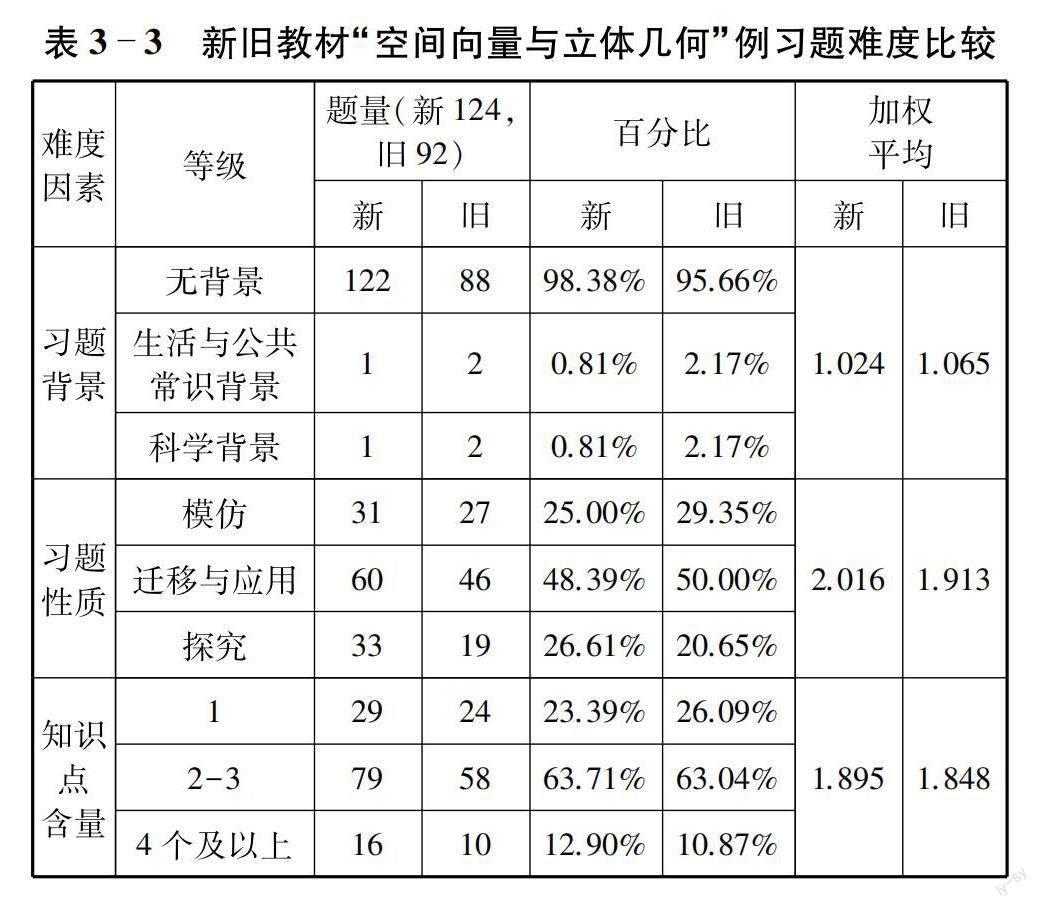
史宁中、郭民（2013）认为习题难度包括习题背景（B）、习题性质（C）、知识点含量（Z）三个维度，其权重β分别为0.4、0.4、0.2^［9］，每个难度因素中的等级赋值依次为1、2、3.习题难度模型为X=β₁·B+β₂·C+β₃·Z.其中习题背景包括无背景、生活与公共常识背景、科学背景；习题性质包括模仿、迁移与应用、探究；知识点含量包括1、2-3、4个及以上.

若一道题目中包含多个小题，均算作一道题，且习题性质按照最深级别统计，所含知识点以表3-2为准.通过统计新旧教材“空间向量与立体几何”例习题，得到表3-3.

新教材例习题难度高于旧教材.通过观察表3-3发现，在习题背景方面，旧教材较难，这是因为旧教材中生活与公共常识背景、科学背景相对较多.但总体来看，两版教材例习题背景大多是纯数学知识.在习题性质方面，新教材较难，可明显看出，新教材探究类题目大幅度增加.在分析题目时发现，探究类题目集中于“空间向量的应用”这一节，这也反映了新教材更關注立体几何中的向量方法.在知识点含量方面，新教材较难，其涉及2-3、4个及以上知识点所占百分比均有所增加，说明新教材更注重知识点之间的联系.通过计算得到，新教材例习题难度X₁=1.595，旧教材例习题难度X₂=1.5608，即X₁＞X₂.故新教材例习题难度高于旧教材.

4 教学建议

基于上述对新旧课标“空间向量与立体几何”内容要求的比较以及对新旧教材“空间向量与立体几何”内容的比较，给出以下教学建议.

4.1 关注数学思想方法的渗透

数学思想方法是数学的灵魂，是数学活动实践经验的概括，是一种文化传承和发展^［10］.本章的数学思想方法包括数形结合思想、化归与转化思想、特殊与一般思想.教师在教学过程中不仅要渗透数学思想方法，还要关注学生能否运用这些思想方法，如将任意两个空间向量之间的问题转化为平面向量问题等.

4.2 关注数学学科核心素养的培养

学科核心素养是育人价值的集中体现，是学生通过学科学习而逐步形成的正确价值观、必备品格和关键能力^［6］.本章的核心素养包括直观想象、数学运算、逻辑推理、数学建模和数学抽象.如直观想象体现在利用向量的几何表示直观地理解空间向量的概念及其运算等；逻辑推理体现在证明直线与平面、平面与平面平行和垂直的判定定理等.

4.3 注重情境创设和问题设计

数学情境融入数学课堂，可激发学生求知欲，提高学习兴趣，且能给学生提供思考与探索的空间等^［11］.新教材本章例习题中所涉及的大都是数学情境.教师在教学过程中应有意识地创设相关现实情境或科学情境，并设计相关问题，使学生感受空间向量在生活中的应用，引导学生用数学的眼光发现问题，用恰当的数学语言描述问题，用数学的思想方法解决问题.

4.4 注重学科间及知识点间的关联性

在课程与教学中运用好跨学科思维是强化学科育人的重要途径，通过数学学科的跨界、融合可以更好地促进学生数学素养的提高^［12］.在本章教学中，教师要注重挖掘相关跨学科知识.如本章的章头图展示的是做滑翔伞运动的场景，联想用平面向量解决物理问题的方法，将平面向量推广到空间向量，从而利用空间向量研究滑翔伞运动.此外，还需注重知识点之间的关联，如向量方法与综合几何方法的共性与差异；用向量法证明所学过的“平面与平面平行的判定定理”等.

4.5 加强立体几何中向量方法的教学

本章的教学，特别是“空间向量的应用”的教学，应注意把具体的立体几何问题作为学习向量方法的载体，通过问题的解决加深对向量法和立体几何内容的理解^［13］.不管是新课标中“空间向量的应用”的内容要求，还是新教材知识点增减及例习题配置情况，都可看出新教材更注重立体几何中的向量方法.教学时要结合例习题，强调综合运用向量及其运算解决几何问题.

参考文献：

［1］ 赵占良.试论教材的功能定位［J］.课程·教材·教法，2021，41（12）：4-10.

［2］ 章建跃.核心素养导向的高中数学教材变革（续2）——《普通高中教科书·数学（人教A版）》的研究与编写［J］.中学数学教学参考，2019（22）：7-13.

［3］ 章建跃.核心素养导向的高中数学教材变革（续3）——《普通高中教科书·数学（人教A版）》的研究与编写［J］.中学数学教学参考，2019（25）：5-11.

［4］ 章建跃.核心素养导向的高中数学教材变革——《普通高中教科书·数学（人教A版）》的研究与编写［J］.中学数学教学参考，2019（16）：6-10.

［5］ 邵光华，张妍.人教A版高中数学新教材特色分析及使用建议［J］.课程·教材·教法，2019，39（12）：109-114.

［6］ 中华人民共和国教育部.普通高中数学课程标准（2017年版）［S］.北京：人民教育出版社，2017.

［7］ 吴立宝，王富英，秦华.数学教科书例题功能的分析［J］.数学通报，2013，52（3）：18-20+23.

［8］ 吴立宝，王富英.数学教材习题“七功能”［J］.教学与管理，2014（31）：66-68.

［9］ 郭民，史宁中.中英两国高中数学教材函数部分课程难度的比较研究［J］.外国中小学教育，2013（7）：55-59.

［10］ 吴增生.数学思想方法及其教学策略初探［J］.数学教育学报，2014，23（3）：11-15.

［11］ 张定强，张元媛，王彤.数学情境教学：理解现状与增润课堂［J］.中小学教师培训，2017（5）：58-61.

［12］ 黄翔，童莉，史宁中.谈数学课程与教学中的跨学科思维［J］.课程·教材·教法，2021，41（7）：106-111.

［13］ 章建跃，李增沪.普通高中教科书教师教学用书.数学：选择性必修.第一册：A版［M］.北京：人民教育出版社，2020.

［14］ 中华人民共和国教育部.普通高中数学课程标准（实验）［S］.北京：人民教育出版社，2003.

［15］ 刘绍学.普通高中课程标准实验教科书 数学 选修2-1 A版［M］.北京：人民教育出版社，2007.

［16］ 章建跃，李增沪.普通高中教科书 数学 选择性必修第一册 A版［M］.北京：人民教育出版社，2020.

［17］ 李甜甜.初中数学教材中的数字文化及其教学研究［D］.伊犁师范大学，2023.

［18］ 蒋莉.高中数学教材三角函数内容的比较研究［D］.伊犁师范大学，2023.

［19］ 陈真丽.基于ISM法的高中数学教材比较研究［D］.广西师范大学，2023.

［20］ 闫晓亭.高中数学教材“立体几何初步”的比较研究［D］.湖北师范大学，2023.

［21］ 向颖怡，叶明露.核心素养视角下的高中数学教材比较分析——以立体几何初步为例［J］.内江师范学院学报，2021，36（8）：25-31+52.