小学数学智慧课堂与GeoGebra深度融合的案例分析

梁仕杰 江晓欣

摘  要：文章主要通过三个小学数学的几何教学案例来说明GeoGebra软件在小学数学教学中的重要作用。其中，在渗透和了解“不完全归纳法”这一数学思想的几何课型中，教师应用GeoGebra软件，不仅能很好地体现出信息技术与学科的深度融合，还能构建出数字化的智慧课堂。使用GeoGebra软件进行教学，能让学生的学习更加高效、直观和有趣，体现出学生的智慧学习和深度学习。

关键词：GeoGebra;智慧课堂;深度学习;不完全归纳法

随着科技的发展，信息技术已经影响着人们生活的方方面面。教育部在《义务教育数学课程标准（2022年版）》中明确指出：合理利用现代信息技术，提供丰富的学习资源，设计生动的教学活动，促进数学教学方式方法的变革。在实际问题解决中，创设合理的信息化学习环境，提升学生的探究热情，开阔学生的视野，激发学生的想象力，提高学生的信息素养。因此，在如今的数学学习中以及信息技术与数学学科融合的前提下，教师和学生的“教”与“学”的方式也在不断改变，平板电脑、VR眼镜、可穿戴电子设备都出现在数学学习活动中。这些技术的出现，为学习者提供了更自主的学习方式、更多的学习资源和更广的学习环境。但是，现在很多的平板课堂、VR课堂，并不是真正意义上的信息技术与学科深度融合的智慧课堂，或是深度学习的教学过程更多的是流于形式。因此，本研究会列出几个GeoGebra软件与小学教学几何教学深度融合的智慧学习、深度学习的案例，以供参考。

一、小学数学中“不完全归纳法”与GeoGebra的深度融合

GeoGebra对比传统的教学，它的优势非常明显，能为学生和教师提供直观的几何模型，真正做到思维可视化，并为学生提供了智慧学习和深度学习的条件。学生在小学数学中通过GeoGebra进行智慧学习，一般需要用“不完全归纳法”来得出相应的结论。

（一）GeoGebra帮助学生掌握三角形的内角和

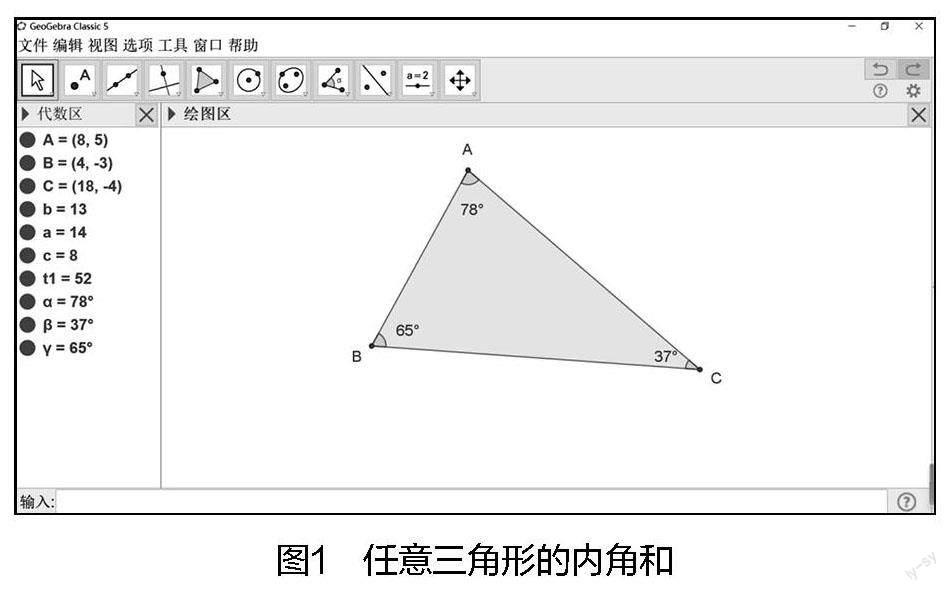
很多教师都研究过“三角形內角和”这一经典课。该课是2014年人教版小学四年级数学下册第五单元“三角形”的最后一个内容。在设计这节课时，教师应思考如何让所有学生掌握任意三角形的内角和是180°，而不是让学生被动接受这个结果。因此，教师可以利用GeoGebra设计“任意三角形的内角和”的课件（如图1）。

在该课件中，学生可以对三角形进行任意位置的拖动，随之，三角形的内角度数也会发生变化。通过计算，学生可以得到，无论拖动出来的三角形是什么类型，其内角和都是180°。在这里，教师会进行一次简单的演绎推理：“同学们的三角形是通过自己随意拖动，在没有设定特定的条件下形成的，但大家的三角形的内角和都是180°，因此有理由认为，任意三角形的内角和都是180°。”

针对“内角和”这一经典课，大部分教师会设计“量算”和“撕拼”这样的教学活动，但由于四年级学生是以直观到抽象的思维过程为主，因此不能进行严格的演绎推理来证明本课的结论。而“量算”和“撕拼”都属于验证的范围，实际操作是有误差的，因此由大量的例子来得出结论就显得尤为重要。而GeoGebra则能为学生提供大量的例子，让学生不完全归纳出“三角形的内角和是180°”这一结论。

在整个探究的过程中，学生都是利用这个课件资源进行智慧学习的。如果学生愿意进行探究，得到的例子将非常多，并可以试图利用这个课件资源去寻找一个反例反驳这一结论，而这个过程正是学生深度学习的过程。学生在探究的过程中，不仅获得了“三角形的内角和是180°”这一结论，还对结论进行了质疑和反思，从而掌握了学习数学的方法，以及养成了反思的思维习惯。

（二）利用GeoGebra让学生直观感受“任意两边之差小于第三边”

同样是“三角形”这一单元的内容，对学生而言，“内角和”的课堂是比较有趣的，而三角形的三边关系则是抽象性和逻辑性都很强。在教材的要求中，学生只要掌握三角形三边关系中的一个即可，即“任意两边的和大于第三边”，而不需要掌握另一个关系——“任意两边之差小于第三边”。由于教材中没有直观的几何模型让学生理解这一关系，因此教材没有安排这一内容。这时教师可以利用GeoGebra为学生制作出探究的课件，让学生的学习内容更完整。

学生在学习“任意两边之和大于第三边”这一关系时，教材事先安排学生学习了“两点之间线段最短”这一公理，然后利用严格的演绎推理来说明“任意两边之和大于第三边”。因此，教师在教授这一课时，也没有用GeoGebra让学生去验证这个关系。而当学习完这一内容时，教师问学生：“既然三角形的任意两边和与第三边有关系，那你还会联想到什么内容？”大部分学生就会想，任意两边的差会跟第三边有类似的关系吗？正是这一个问题，引出了下一节课的教学方向。

在教学“三角形任意两边之差小于第三边”这一内容时，教师可以为学生提供以下的Geogebra课件和学习单（如图2）。在该课件中，学生可以对三角形进行任意拖动，形成不同类型和不同大小的三角形，而对应的三角形的各边的长度也随之变化。学生记录下每次拖动的三角形的数据，并在表格中进行计算和分析。

在整个探究过程中，学生利用了GeoGebra课件资源进行自主和个性化的探究和分析，最终得到结论。由于课堂时间只有40分钟，留给学生探究的时间不多，因此学生可以在课后继续分析。学生通过对各个例子的分析与不完全归纳，很容易就得到了“任意两边之差小于第三边”的这一结论。

上述过程，已经体现了学生的智慧学习。同时在课堂上，有部分学生自觉地把上节课学习的“任意两边之和大于第三边”和本节课得到的“任意两边之差小于第三边”进行了对比和整合，最终得到了小学阶段很少出现，而学生又可以理解的结论：三角形任意边的取值范围——两边差<第三边<两边和。这是学生对获得的新知和旧知进行对比和联系，从而再获得新知的过程，也正是本节课学生进行深度学习的一个体现。

（三）GeoGebra为学生直观呈现正方体表面的涂色问题

在2021年人教版小学五年级数学下册第三单元的“长方体和正方体”中，有这样一个“探索图形”的活动课。该课是让学生探索这样的一个问题：将n阶正方体的表面涂上颜色，探究其三面涂色的小正方体个数、两面涂色的小正方体个数、一面涂色的小正方体个数和没有涂色的小正方体个数分别有几个。

首先，这个问题在教材中的作用是，通过解决这个问题培养学生的数学思想;其次，培养学生能够利用发现的规律解决问题。对这个问题，学生认为无从下手，教师也会认为很难在课堂上组织有效的教学。根本原因是，这是对立体图形的探究，学生很难在脑海中直观地想象，教师能提供的直观的教具也有限（可能只有1阶、2阶、3阶的正方体），难以让学生进行有效的觀察并总结规律。为了解决上述问题，教师可以在堂课中为学生提供三种学习资源：一是由125个小正体堆积而成的大正方体，其中表面涂上了颜色，这一资源的应用是为了帮助空间想象能力比较弱的学生，在课堂上真正实现“做中研、做中学”;二是教师利用VR眼镜，提供沉浸式的学习资源，让学生戴上眼镜观察1至10阶正方体的情况，最后总结出结论;三是教师利用GeoGebra的课件，提供一个可以改变阶数、自由聚合与离散的正方体，让学生进行探究。

根据学生的上课情况来看，这三种资源都有学生使用，但大部分学生都会选择在平板电脑上使用GeoGebra课件进行探究，原因是学生认为这样的课件比实物的小正方体更方便，相对于VR眼镜，不用转换场景，不会打断学习的过程。下面是提供给学生的GeoGebra课件。

可以看到，正方体为聚合状态时，其表面涂了颜色的情况（如图3）;当正方体处于离散状态时，正方体表面涂色和内部涂色的情况（如图4）。由于这个课件可以自由旋转，学生在实际操作中，可以任意观看正方体上下左右前后的涂色情况，从而能直观观察出各种涂色的小正方体处在大正方体中的位置。这样不仅能为学生直观展示小正方体的情况，还能为学生进一步探索规律、形成数学思维提供有效的素材。

二、教学反思

本节课对学生而言，难点在于难以想象、难以观察和难以描述。而教师利用GeoGebra课件，则可以帮助空间想象能力较弱的学生直接观察，方便学生准确地描述发现。同时在该课中，学生不仅使用GeoGebra课件进行了探究学习，还在这样的探究活动中，具有了以下的数学思维：一是用化繁为简的方法进行数学问题的探究;二是对数学信息进行不完全归纳，得出结论;三是用字母表示最终的发现，以便实际运用。学生在对问题的探究中，有所发现和总结，并能得出结论和解决实际问题，这正是这堂课学生的智慧学习和深度学习的体现。

对这堂课，有点遗憾的是，学生未能完全使用GeoGebra课件进行更深入的探究。该课件除了能显示各阶数正方体的涂色情况外，还能调整正方体长宽高的参数，让本节课的结论得到更多的结果。

在本研究原来的设想中，是让学生将自己的发现联系起来，得到下面的等式：

（n-2）3=n3-6n2+12n-8

但这个二项展开式已经超出小学生的认知水平，因此课堂的最后并没有再延伸下去，但这为学生以后学习这方面的内容提供了一个很好的几何直观模型。

三、结语

通过上面的几个课例可以看出，小学的几何教学可以用Geogebra提供的资源让学生进行学习，但不是所有的几何教学都能用上。例如，上面提到的“三角形任意两边之和大于第三边”这一堂课就无法使用，原因是课本提供了线段公理给学生，学生已经可以进行严格的演绎，推理得出结论，这时如果再使用GeoGebra来进行“不完全归纳”，就显得思维层次较低。在小学教学中，关于呈现几何动态过程的内容，教师也可以使用GeoGebra进行教学，如平行四边形的面积、圆面积、圆柱体积等课型，都可以使用这个软件。

本课例是对GeoGebra与小学数学教学深度融合的一次初步尝试，希望通过本研究的论述，能为各数学教育工作者提供一些启示和帮助。

参考文献：

[1]李凯. 《义务教育数学课程标准（2022年版）》中课程实施的新变化[J]. 中学数学月刊，2023（04）：8-11.

[2]单慧. GeoGebra软件在小学数学教学中的应用[D]. 苏州：苏州大学，2017.

[3]周瑶. GeoGebra辅助小学数学教学的实践策略研究[J]. 考试周刊，2020（87）：68-69.

（责任编辑：邹宇铭）