过程分步探究,解法深入思考
王莹






[摘 要] 开展二次函数综合题解题探究可以帮助学生强化基础,提升解题思维. 问题探究过程,建议采用基础强化与思想方法指导相融合的方式,立足基本问题,合理构建模型,分步解析过程,教学解题思维. 文章以一道二次函数综合题为例,开展解题突破,并深入探讨,提出相应的教学建议.
[关键词] 二次函数;抛物线;旋转;K字形模型;思想方法
试题呈现
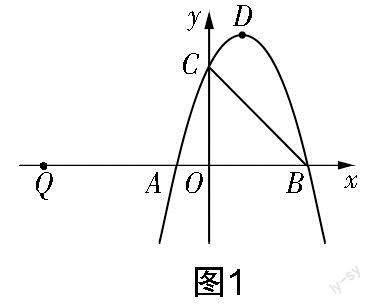
试题 如图1所示,已知二次函数y=mx2+(m2-m)x-2m+1的图象与平面直角坐标系的x轴交于点A和点B,与y轴交于点C,顶点D的横坐标为1.
(1)求二次函数的解析式以及点A,B的坐标;
(2)若P(0,t)(t<-1)是y轴上一点,已知Q(-5,0),将点Q绕着点P顺时针旋转90°后得点E,若点E恰好落在该二次函数的图象上,试求t的值;
(3)在(2)的条件下连接AD,AE,若M是该二次函数图象上一点,且∠DAE=∠MCB,试求点M的坐标.
解析突破
上述为二次函数综合题,涉及抛物线与直线相交、点旋转、等角等内容,三小问由易到难,关联性较强. 解决时建议立足条件解析问题,结合图象逐步突破.
1. 探求解析式
2. 模型定坐标
第(2)问探究点的坐标,旋转后所得的点在二次函数的图象上,核心条件有三个,需要分别进行解读.
条件①:由点P(0,t)(t<-1)可知P是y轴上的点,且t为小于-1的数.
条件②:点Q(-5,0)绕点P顺时针旋转90°后得到点E. 根据旋转特性可知PQ=PE,且∠EPQ=90°. 若连接QE,进一步可知△QPE为等腰直角三角形.
条件③:点E在二次函数的图象上,可知点E的坐标满足二次函数的解析式.
根据上述条件可知如下信息链:点Q,P的坐标→点Q旋转→点E在抛物线上. 显然问题的突破口是确定点E的坐标,于是解析突破可分如下三步.
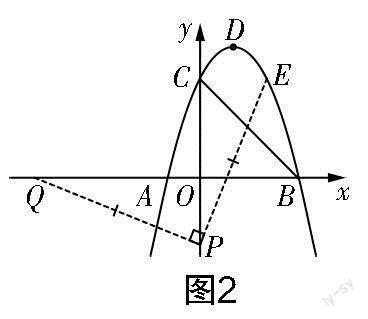
第一步,根据题意绘制图2.
第二步,构建模型求点E的坐标.
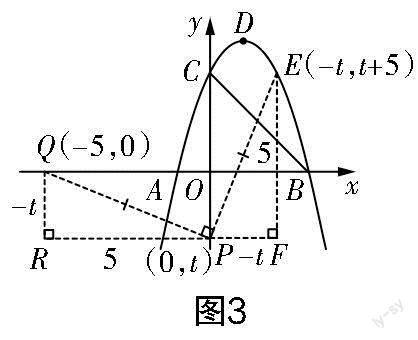
由上述分析可知△QPE为等腰直角三角形,于是可构造“K”形全等模型,过程如下. 过点P作x轴的平行线,再分别过点Q和点E作该平行线的垂线,设垂足分别为R,F,如图3所示. 由模型特性可证△QRP≌△PFE,于是可推知PF=QR,EF=PR. 已知Q(-5,0),P(0,t),所以PF=QR=-t,EF=PR=5,进一步分析可知点E的坐标为(-t,t+5).
第三步,将点坐标代入解析式求t值.
已知点E在二次函数的图象上,将点E的坐标(-t,t+5)代入函数解析式y=-x2+2x+3中,可解得t=-1(舍去)或t=-2,所以t的值为-2.
3. 定量探等角
第(3)问是等角存在性问题,建立在第(2)问条件的基础上,探究二次函数图象上的点M,使得∠DAE=∠MCB. 问题解析可以采用“把握不变量”与“确定性思想”的策略,即对于成立条件∠DAE=∠MCB,∠DAE的三个顶点A,D,E的坐标是确定的,故为定角,则∠MCB的大小一定,同时该角中与之相关的点B和点C也是定点,故点M的坐标可确定,可求出. 基于上述分析,解析突破可分如下几步.
第一步,三角形特性分析.
第二步,建模推坐標.
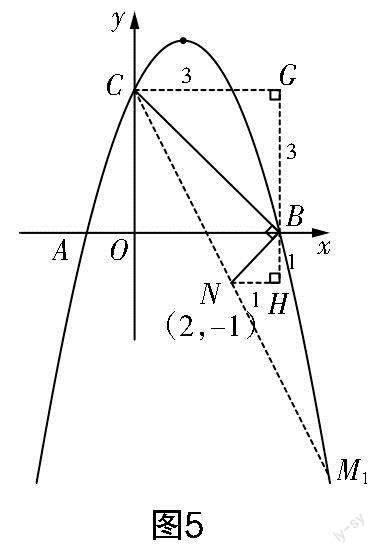
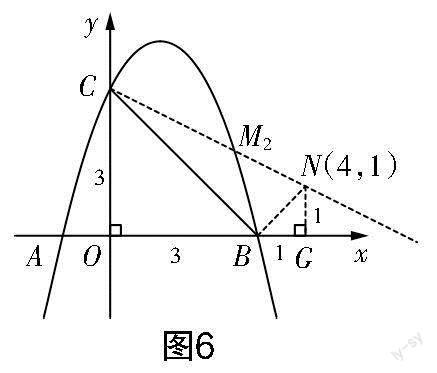
点M在二次函数的图象上,显然有两种情形:一是点M在点B的下端(M1),二是点M在点B的上端(M2).
解后思考
上述对一道二次函数综合题进行了解法探究,试题的后两问为核心之问. 上述在解析时充分利用了“K”形模型,其中第(2)问依托旋转的点、线构造了“K”形全等模型,由全等三角形的性质推导线段长;而第(3)问则依托直角三角形构造了“K”形相似模型,利用相似比推导线段长. 整个解题过程,利用“K”形模型实现了线段的“化斜为直”,巧妙地利用模型特性推导线段长.
“K”形模型是几何中重要的模型之一,模型特性可广泛应用于解题. 从模型特征来看,两直角三角形共定角,且一边共线,形成了一个90°的夹角,由条件可证得两三角形有两种特殊关系:①全等关系(有一组对边相等);②相似关系. 实际解答时,可依托相似或全等关系推导与边、角相关的条件. 而在函数问题中合理使用“K”形模型,可以避免烦琐的坐标运算,并借助模型特性实现线段“化斜为直”,直接获得线段长. 实际解答时,可以按照“图形分析→模型构建→特性推导→问题解答”四步进行,具体如下.
第一步,图形分析
由“K”形模型的特性可知,模型构建的基础为直角,故分析图形时关注其中的90°角或直角三角形.
第二步,模型构建
依托图形中的90°角或直角三角形构建“K”形模型,建模过程尽量采用补形的思路,依托三角形的顶点,作“水平—垂直辅助线”,实现线段“化斜为直”.
第三步,特性推导
该步主要利用模型的特性来证明一组三角形相似或全等,充分把握模型中的边角关系.
第四步,问题解答
依托上述所证的三角形相似或全等,推导与线段、角度相关的条件,进一步转化推理,即利用其中的线段长求点坐标,利用等角关系求三角函数值等.
教学建议
上述对一道二次函数综合题开展解题探究,呈现了试题解析突破的思维过程,并深入探究了“K”形模型,下面基于课堂实践开展教学探究,提出几点建议.
1. 强化基础知识,关注知识综合
二次函数综合题往往所涉考点较多,解析难度较大,在实际解析时需要合理处理条件. 探究教学需要立足基础知识,开展条件解读,灵活利用基本方法逐步拆解问题. 以上述试题为例,教师需引导学生利用待定系数法求解析式,结合旋转知识分析其中的几何特性,灵活运用全等或相似推导条件等. 同时,注意教学中的知识综合,指导学生关注知识间的关联,完善知识体系,尤其是综合性较强的函数类问题,从几何与代数视角综合分析.
2. 总结几何模型,活用模型特性
几何模型在解题中有着广泛的应用,利用模型特性可推导出直切问题本质的条件,上述在解析后两问的过程中充分引入了“K”形模型,利用模型的相似或全等特性推导出了关键条件. 而在实际教学中,教师要引导学生从以下几个方面开展模型探究:一是关注模型特征,即关注模型的特点、构建的条件;二是总结模型特性,即从几何角度证明模型特性;三是重视建模过程. 解题建模是教学的关键,教师需指导学生掌握建模技巧,构建合理模型.
3. 渗透数学思想,提升综合素养
综合题的解题过程中需要用到一定的数学思想,利用思想方法可以较为简捷地完成问题分析、条件转化、模型构建、问题解答. 以上述二次函数综合题为例,突破过程涉及化归转化、模型构建、数形结合、分类讨论等思想,解题时需在众多数学思想的指导下完成思路构建. 所以教学中教师要合理渗透数学思想,引导学生感悟思想内涵,掌握思想方法的运用技巧,依托数学思想开展思维培养,全面提升学生的综合素养.

