柯西不等式的特例
——方差不等式的简单应用
2023-11-11 06:09:56刘大伟李勇霞
高中数理化 2023年19期
刘大伟 李勇霞
(1.重庆市江津中学校 2.重庆市巴蜀科学城中学校)
在概率论和统计学中,随机变量的方差描述的是数据的离散程度,它能够反映数据波动情况的特征数与期望之间的关系,即该变量离其期望值的距离.同时,方差与不等式也有着密不可分的联系.本文利用方差公式推导出方差不等式,并将之应用于一类函数最值问题的求解过程中,拓宽了解题思路和方法,最后进一步阐述了两者之间的关系,提出了方差不等式为柯西不等式的特殊情况这一结论.方差的定义:
因为S2≥0,所 以,当x1=x2=…=xn时,等号成立.
该不等式称为方差不等式,应用方差不等式可以快速求解一类函数最值问题.
1 方差不等式的简单应用
例1 求函数y=x-1+ 5-x的最大值.
解 由方差不等式可知
例2 求函数y=x-1+ 9-3x的最大值.
解 原函数可化简为
由方差不等式可知
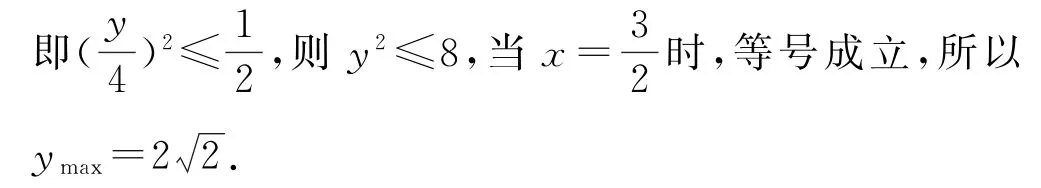
易错点 对于本例,如果直接利用方差不等式会出现问题,即
再由其定义域{x|1≤x≤3},求得ymax=2 3.
该解法错在两次不等式等号成立的条件是不同的,所以在运用方差不等式解题的过程中需要注意前提条件为定值.
2 方差不等式的应用总结
结合上面的两个例题,下面给出该类型函数一般形式的求解定理.
证明 原函数等价于
由方差不等式可知即
3 方差不等式的推广应用
若x1+x2+…+xm=m,则
若x1+x2+…+xm=a,则

4 方差不等式与柯西不等式的关系阐述
方差不等式是柯西不等式的特殊情况.
对于柯西不等式
当且仅当a1=a2=…=an=0或bi=kai(k为常数,i=1,2…,n)时,等号成立.
由方差不等式得
当x1=x2=…=xn时,等号成立.
在教学过程中为培养学生的化归和转化能力,锻炼学生的发散思维能力,提高学生的数学素养,教师要有意识地培养学生用“跨界”知识解决问题的能力.
(完)
猜你喜欢
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26 14:03:32
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08 01:28:48
卷宗(2020年34期)2021-01-29 05:36:24
河北理科教学研究(2020年3期)2021-01-04 01:49:38
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15 22:17:33
高师理科学刊(2020年2期)2020-11-26 06:01:26
语数外学习·高中版中旬(2020年2期)2020-09-10 07:22:44
河北理科教学研究(2020年1期)2020-07-24 08:14:34
中学生数理化·高一版(2019年4期)2019-01-11 19:26:25
中央民族大学学报(自然科学版)(2017年2期)2017-06-11 07:14:46

