“鳖臑”闹课堂——“鳖臑模型的应用及探究”教学实录

陈秋月 汪庭斌

(安徽省宁国中学)

数学文化类试题是近几年高考试题中的热点问题,教师应积极挖掘教材中的数学文化素材,巧妙融合数学知识,融会数学思想方法,发挥数学文化的育人作用.本节课借助鳖臑模型的应用与探究,为学生提供自由表达、质疑、探究、讨论问题的机会,让学生感受数学文化的魅力、数学学习的快乐,让数学学科核心素养在教学中全方位渗透.

1 高考题中的鳖臑

例1 (2015年湖北卷文20)«九章算术»中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图1所示,在阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD＝CD,点E是PC的 中 点,连 接DE,BD,BE.

图1

(1)证明:DE⊥平面PBC,试判断四面体EBCD是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;

(2)记阳马P-ABCD的体积为V1,四面体E-BCD的体积为的值.

设计意图 柏拉图说:“良好的开端,是成功的一半.”在课堂情境的设置中,笔者以一道高考试题抛砖引玉,题中的“阳马”“鳖臑”引起学生的关注,充分调动大家的学习兴趣,为后面模型来源、应用和探究的层层递进,螺旋式上升做好铺垫.

2 鳖臑的来源

鳖臑是我国古代数学中非常重要的模型,在多本著作里都有阐述.

«九章算术»中记载“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”东晋时期著名数学家刘徽说到“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.中破阳马,得两鳖臑,鳖臑之起数,数同而实据半,故云六而一即得.”

师生共同观看视频——鳖臑的生成过程.

设计意图 用动态的视频生动形象地演示出中国古代数学文化中的堑堵、阳马、鳖臑的生成.堑堵、阳马、鳖臑实际上是中国古代对一些特殊几何体的称呼,通过视频的播放让学生更直观地感受到“陌生”的鳖臑实际上是我们再熟悉不过的立体几何体.

3 鳖臑的定义

师:同学们,现在知道了堑堵、阳马和鳖臑的来源了,那么如何准确地定义它们呢?

小组热烈讨论交流,给出了它们的定义.

生:堑堵是两底面为直角三角形的三棱柱.

生:阳马是底面为长方形,两个三角面与底面垂直的四棱锥体.

生:鳖臑是四个面都为直角三角形的三棱锥.

师:同学们描述得很准确,它们实际上都是我们熟悉的几何体(如图2).

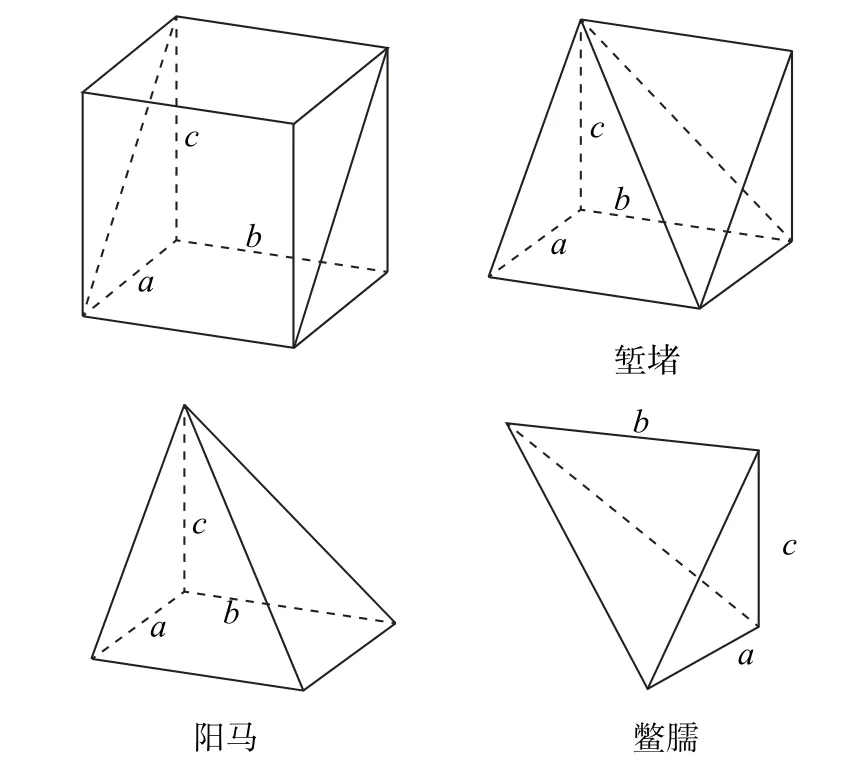
图2

设计意图 从动态的视频中提炼出堑堵、阳马、鳖臑的静态图形,以便学生更细致地观察、认识、探究,抓住它们的几何特征,给出精准的定义.

4 教材中的鳖臑

例2 (人教A 版数学必修第二册第158页例8)如图3所示,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.

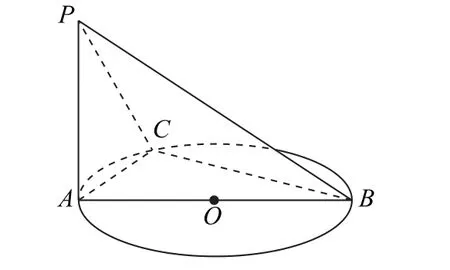
图3

师:请同学们仔细观察一下三棱锥P-ABC,发现它有什么几何特征吗?

生:它的四个面都是直角三角形,它是鳖臑.

师:回答得非常好,三棱锥P-ABC就是鳖臑模型.

大家再观察一下,鳖臑还有其他等价的定义吗?

生:三棱锥中一侧棱与底面垂直,底面为直角三角形.

师:精准吗?

生:侧棱应该垂直于底面锐角顶点处.

师:非常棒!

例3 (人教A 版数学必修第二册第158 页练习3)如图4 所 示,AB⊥平 面BCD,BC⊥CD,你能发现哪些平面互相垂直,为什么?

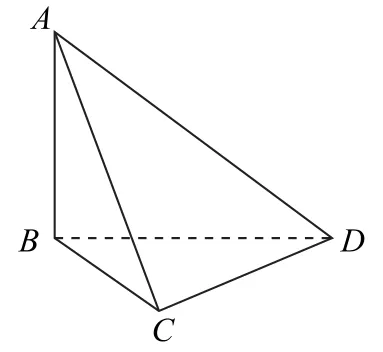
图4

三棱锥A-BCD也是鳖臑,更进一步深化了对鳖臑模型的认识.

设计意图 挖掘教材中文化资源,以课本上的例题和练习题为载体,引导学生进行探究,发现规律,深化学生对鳖臑模型的认识,体验数学文化,也为下一步学生自主探究做好铺垫.

5 鳖臑的深度探究

追问1:如何判断一个三棱锥A-BCD是鳖臑呢?

生:定义法,它是四个面都为直角三角形的三棱锥.

师:很好,还有吗?

生:AB,CD,BC两两垂直.

生:AB⊥平面BCD,且BC⊥CD.

生:AB⊥平面BCD,将BC⊥CD改成AC⊥CD也可以.

生:AB⊥平面BCD,且平面ABC⊥平面ACD.

师:同学们归纳总结得特别好、特别全面,这些都可以证明,若三棱锥A-BCD的四个面都是直角三角形,则它是鳖臑.

师:在鳖臑模型中有着求解立体几何问题的核心关系——垂直关系.

追问2:在上述鳖臑几何体的棱和面中,有哪几组线线垂直、线面垂直、面面垂直呢?

生:线线垂直中相交垂直有四组:AB⊥BD,AC⊥CD,AB⊥BC,BC⊥CD;异面垂直的只有一组:AB⊥CD.

生:线面垂直有两组:AB⊥平面BCD,CD⊥平面ABC.

生:面面垂直有三组:平面ABC⊥平面ACD,平面ABC⊥平面BCD,平面ABD⊥平面BCD.

师:同学们太棒了,大家总结的这些垂直关系都是鳖臑的丰富性质.

设计意图 通过一连串的追问,引导学生借助鳖臑这一几何体中丰富的(线线、线面、面面)垂直关系,让学生熟悉垂直关系下的定理和性质的应用,充分发挥课本习题的教育功能和教学价值.

6 鳖臑模型的应用

师:同学们,2015年湖北卷文科试题就以鳖臑作为命题的背景(例1),引起了广泛关注,当年很多学生没见过这两个字,因此影响了答题的心情.今天我们已经了解并掌握了鳖臑的定义和性质,我们应该有信心解决这道高考题.

生:要证线面垂直,只需证线线垂直.因为PD⊥底面ABCD,所以PD⊥BC,又底面ABCD是长方形,得CD⊥BC,而PD∩CD＝D,所以BC⊥平面PCD.又DE⊂平面PCD,所以BC⊥DE.

因为点E是PC的中点,且PD＝CD,所以DE⊥PC.而PC∩BC＝C,所以DE⊥平面PBC.

由DE⊥平面PBC,DE⊂平面PCD,可知四面体EBCD的四个面都是直角三角形,即四面体EBCD是鳖臑,其四个面的直角分别是∠BCE,∠BCD,∠DEB,∠DEC.

师:证明得非常严谨、规范,对阳马和鳖臑这两个模型掌握得非常好,那第(2)问谁来挑战一下?

设计意图 这是一道与阳马、鳖臑模型有关的高考题,体现了新课程要重视数学文化这一重要基本理念.高考中对数学文化的考查要求,也显示出数学文化在高考试题中独特的地位.在问题的探究中,学生更加熟习立体几何体中的垂直关系、定理和性质的应用.

7 课后作业

1)回归课本

人教A 版数学必修第二册中有许多相关问题.

1.(第160页例10)如图5所示,已知PA⊥平面ABC,平面PAB⊥平面PBC,求证:BC⊥平面PAB.

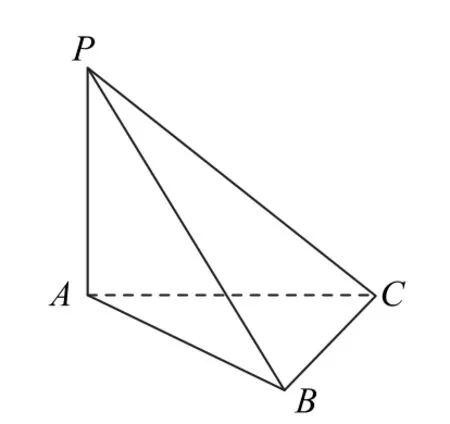
图5

2.(第164 页第20题)如图6 所 示,AB是 圆O的直径,点C是圆O上的动点,过动点C的直线VC垂直于圆O所在平面,D,E分别是VA,VC的中点.判断直线DE与平面VBC的位置关系,并说明理由.

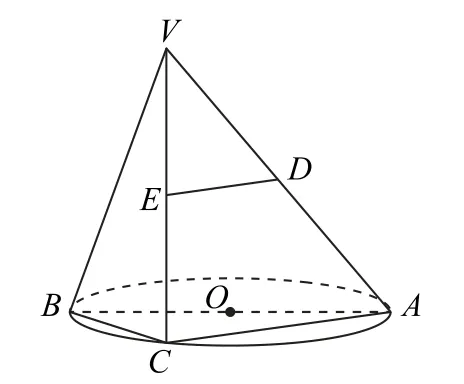
图6

3.(第170页第9题)如图7所示,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点求证:

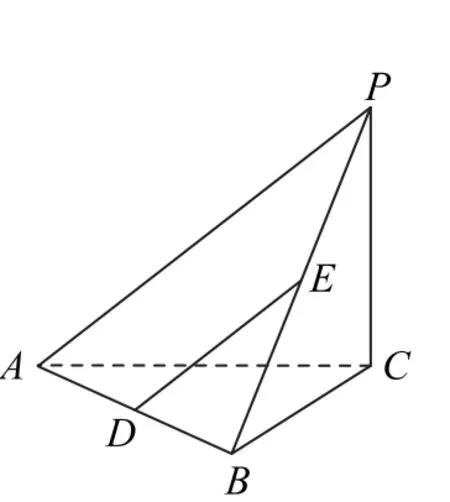
图7

(1)DE//平面PAC;

(2)AB⊥PB.

4.(第171页 第13题)如图8 所示,在三棱锥P-ABC中,∠ACB＝90°,PA⊥底面ABC.

图8

(1)求证:平面PAC⊥平面PBC;

(2)若AC＝BC＝PA,M是PB的中点,求AM与平面PBC所成角的正切值.

2)课后拓展

如图9所示,PA⊥圆O所在的平面,AB是圆O的直径,C是圆周上一点,其中AC＝3,PA＝4,BC＝5.

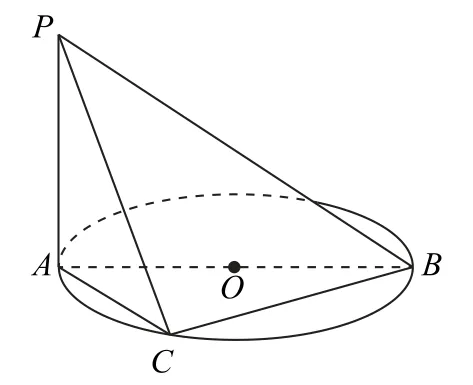
图9

(1)求PB与平面PAC所成角的正弦值;

(2)求该几何体的外接球的半径;

(3)求该几何体的内切球的半径.

设计意图 这些题目都是鳖臑模型,相当于设置了“微专题”,对所学的知识和应用起到巩固和强化的效果,同时又布置了课后拓展题,求鳖臑模型中的线面角及外接球和内切球的半径,这也是为鳖臑模型下一步的延伸拓展探究做铺垫.

本节课中通过鳖臑模型的导引对高考题中的鳖臑、教材中的鳖臑进行了探究,在探究的过程中,通过对鳖臑模型的观察、发现、探索、实践揭示了鳖臑模型的本质.通过鳖臑模型这一载体挖掘了立体几何中线线垂直、线面垂直、面面垂直以及三种垂直关系的相互转化,更加熟练地使用判定定理和性质,提升学生思维能力和解题能力.将数学文化融入课堂教学中,得到了学生的认可,大大激发学生探究立体几何的热情,教师的教和学生的学融为一体,我们的课堂也因此更加精彩,创造真正高效、高质量、灵动的课堂.

(完)