一道高考题的解法与拓展

张露梅 何拓程(特级教师)

(1.中央民族大学附属中学 2.北京理工大学附属中学)

高考题是命题专家精心命制的,充分体现了数学学科核心素养,蕴含了丰富的数学思想,具有很高的信度和效度.挖掘高考试题的数学教育价值,并提出具有探究性的问题,引导学生开展探究活动,使学生在掌握知识的同时学会研究,提高其发现问题、分析问题和解决问题的能力,以达到进一步理解数学的目的.本文以2020年高考数学北京卷第20题为例,进行一些探讨.

1 原题再现

(1)求椭圆C的方程;

(2)过点B(－4,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x＝－4于点P,Q,求的值.

2 解法探究

分析 第(1)问,根据条件列出a,b,c的关系式,从而求出椭圆的标准方程.第(2)问,要求的值,等价于求,因此需要由直线MA,NA的方程确定点P,Q的纵坐标.

(2)如图1 所示,设M(x1,y1),N(x2,y2),P(－4,yP),Q(－4,yQ),MB的斜率为k,则直线l的方程为y＝k(x＋4),MA的方程为

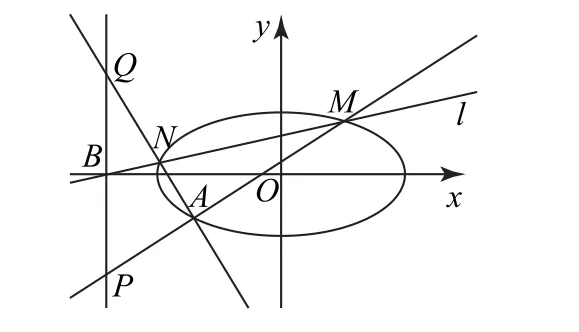
图1

令x＝－4,可得

如果充分研究几何条件并将其代数化(坐标化),同样得到这样的结论.过点A作垂直于x轴的直线m与直线l相交于点T(如图2),利用三角形相似可将竖直方向的比值转化为水平方向的比值.

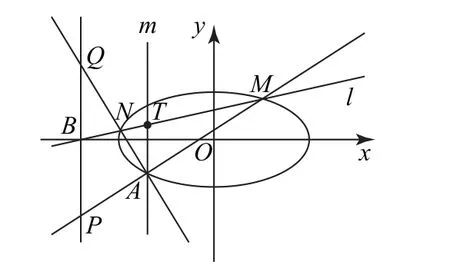
图2

设T(－2,yT),则

可得

由于出现了4x2＋2x1,4x1＋2x2,即x1,x2的系数不均衡的情况,无法直接运用根与系数的关系,解题出现了困境,如何突破难点?

探究1 “凑”根与系数的关系,分而治之

由题可知直线l的斜率必存在,设斜率为k,则直线l的方程为y＝k(x＋4),与椭圆方程联立,可得(4k2＋1)x2＋32k2x＋64k2－8＝0,由

基于消元思想,利用根与系数的关系,将这个比值转化为只含一个根和斜率k的式子,这种方法虽然计算量较大,但是思维量较小,是必须掌握的通性通法.

探究2 “用”根与系数的关系,整体代换

同探究1,可得

消去k2可得

探究3 “审”原题条件,特值引路

显然yPyQ＜0,取MN斜率为零的特殊情况,可以求出比值为1,即,因此转化为证明yP＋yQ＝0,即可直接利用根与系数的关系.

同探究1,可得

其中

从而yP＋yQ＝0,所以.这里要求学生有很强的审题意识,充分挖掘题目内在的联系,同时对学生的思维能力也有较高的要求.

3 还有话说

3.1 变换题设条件与结论

将上述高考题中第(2)问变成:过点B(m,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x＝m于点P,Q,若,求m的值.

设M(x1,y1),N(x2,y2),由探究3,先用特值引路,取MN斜率为零的特殊情况,因为

解出m＝－4.

一般地,设直线MN的斜率为k,则直线MN的方程为y＝k(x－m),与椭圆方程联立可得

当Δ＝(－8mk2)2－4(4k2＋1)(4m2k2－8)＞0时,可得k2(m2－8)－2＜0,此时方程有两个不相等的实根,则

又直线MA的方程为

令x＝m,则

同理,有

所以yP＋yQ＝(m＋4)[－4k(m＋2)＋4]＝0恒成立,故m＝－4.

3.2 拓展题目的结论

再将上述高考题中第(2)问变成:过点B(m,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x＝m于点P,Q,若,探求m与λ的关系.

设M(x1,y1),N(x2,y2),先用特值引路,取MN斜率为零的特殊情况,因为

所以

显然,当λ＝1时,即为3.1中的问题.

另外,由上式知λ≠(2＋1)2,感兴趣的读者可以尝试思考一下,当λ＝(2＋1)2时是什么样的情形.

4 我的思考

4.1 理解数学,突出本质

数学的本质是从变化的数学对象中探求不变的性质,理解数学要从理解数学的本质开始.本题第(2)问不落俗套地选择不能直接运用根与系数的关系来考查学生探究能力,很好地考查了学生的数学素养.数学素养就是对数学本质的理解和把握.学生在高考中不能顺利完成问题求解,究其原因,其实是没有真正理解这类问题的数学实质,如果教师在教学过程中也能对所做的题目进行一些类似的变形和拓展研究,相信一定能更深刻地理解数学.因此,认真探究这类题的不同解法以及拓展是很有必要的.

4.2 理解学生,突破难点

高中数学课程面向全体学生,要以学生发展为本,立德树人,提升素质,实现人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.不同学生可以选择不同的解题方法,本题中探究1起点低,容易入手,难点是运算,若运算能力不强,可研究探究2和探究3.事实上,从笔者所教的学生高考情况来看,由于学生基础差别很大,同样的讲解,得分差别却非常大,可见,理解学生,实际上是要了解他们的需求,根据不同基础的学生提供不同的指导方案.当然,探究2也不是无本之木,如2015年北京卷文科第20题.

题目 已知椭圆C:x2＋3y2＝3,过点D(1,0)且不过点E(2,1)的直线与椭圆C交于A,B两点,直线AE与直线x＝3交于点M.

(1)求椭圆C的离心率;

(2)若AB垂直于x轴,求直线BM的斜率;

(3)试判断直线BM与直线DE的位置关系,并说明理由.

分析 第(3)问要证DE//BM,如图3所示,可利用几何性质

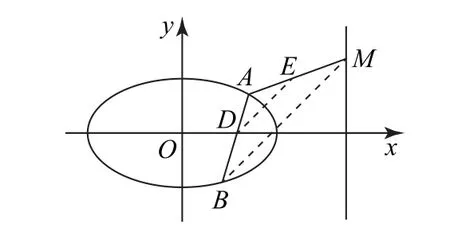
图3

类似于探究2.

4.3 理解教学,使学生会思考

数学教学的本质就是在教师的帮助下,学生通过学习,揭示数学规律,总结数学方法,形成良好的数学思维的过程.因此,教学是一种不断变换角度的过程,只有不断地调整教师的已有的观点来适应不同学生,才能做到真正地理解教学.这道高考压轴试题难度高,一般学生难以发现解题突破口,我们可以把它作为一个资源进行再开发,引导学生结合题目中图形的几何特征,理顺曲线与直线之间的位置关系,理解运算对象,由易到难设计启发性问题,让学生主动探究,分析出合理的转化方向,在运算的过程中积累数学运算经验.如此,教师就能真正地理解数学教学,也能引导学生学会思考,从而构建真正意义上的理解教学.

(完)