权方和不等式巧解高考题

林国红

(广东省佛山市乐从中学)

高中阶段有一些重要的不等式,如均值不等式和柯西不等式,这些不等式在解题时能发挥重要的作用.此外,我们还经常看到一个特殊的不等式——权方和不等式的身影.特别是近几年高考题、各省市模拟试题中有些不等式题悄然出现权方和不等式的结构形式.权方和不等式将向量不等式、柯西不等式及其变式统一起来,是一个结构对称、形式优美的重要不等式.如果能够根据题设、结论的结构特征,巧妙配凑目标式子使之具备权方和不等式结构特征,再灵活选用权方和不等式解题往往能使解题过程简洁明了,能起到事半功倍的效果.

若ai,bi∈R∗(i＝1,2,…,n),且m＞0,则

1 权方和不等式求最值

例1 (2018年江苏卷理21)若x,y,z为实数,且x＋2y＋2z＝6,求x2＋y2＋z2的最小值.

因为x＋2y＋2z＝6,由权方和不等式,得

例2 (2019年全国Ⅲ卷文、理23)设x,y,z∈R,且x＋y＋z＝1.

(1)求(x－1)2＋(y＋1)2＋(z＋1)2的最小值;

成立,证明:a≤－3或a≥－1.

2 权方和不等式证明不等式

例3 已知a,b,c均为正数,且a＋b＋c＝1,证明

证明 因为a＞0,b＞0,c＞0,且a＋b＋c＝1,所以由权方和不等式,可得

例4 (2017年全国Ⅱ卷文、理23)已知a＞0,b＞0,a3＋b3＝2,证明:

(1)(a＋b)(a5＋b5)≥4;

(2)a＋b≤2.

证明 (1)略.

(2)因为a＞0,b＞0,所以由权方和不等式,可得

于 是(a＋b)3≤8,即a＋b≤2,当 且 仅 当即a＝b＝1时,等号成立.

例5 (2019年全国Ⅰ卷文、理23)已知a,b,c为正数,且满足abc＝1,证明:

证明 (1)略.

(2)因为a,b,c为正数,于是a＋b＞0,b＋c＞0,c＋a＞0,所以由权方和不等式与均值不等式,可得

例6 (2022年全国甲卷文、理23)已知a,b,c均为正数,且a2＋b2＋4c2＝3,证明:

(1)a＋b＋2c≤3;

(2)若b＝2c,则

证明 (1)因 为a,b,c均 为 正 数,且a2＋b2＋4c2＝3,所以由权方和不等式,可得

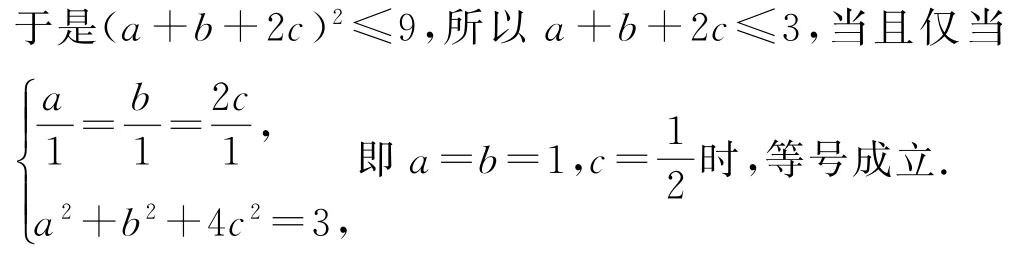
(2)证法1 因为b＝2c,且a2＋b2＋4c2＝3,所以a2＋8c2＝3.

由权方和不等式,可得

证法2 由(1)可知a＋b＋2c≤3,又b＝2c,所以0＜a＋4c≤3,即

由权方和不等式,可得

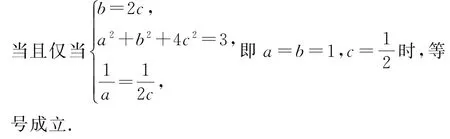
权方和不等式在解决分式型不等式中占有重要地位,要根据题目的条件或结论灵活变形,使其符合权方和不等式的应用形式.对于一些整式的问题,需要先化为相应的分式,因为整式可以看成分母为1的分式,而且1的任何次幂都是1,从而便于利用权方和不等式.

权方和不等式是一个很重要的不等式,可用于处理分式不等式、放缩求最值、证明不等式等问题,在高考中有着广泛的应用.权方和不等式形式简洁、结构漂亮,合理使用权方和不等式可以避免不等式放缩过程中许多技巧性很强的凑配.从上述例子,可以充分体会权方和不等式的“魅力”,用一句话来概括:用权方和不等式,简万般繁杂运算.直接用“简洁明了”,配凑用“小巧玲珑”,变换用更是“威力无穷”.

(完)