焊接机器人运动学仿真及控制系统研究

王军，邵超祥，张亮，李超

1.河北科技大学 材料科学与工程学院，河北 石家庄 050018

2.河北科技大学 河北省材料近净成形技术重点实验室，河北 石家庄 050018

3.河北省焊接钢管技术创新中心 衡水京华制管有限公司，河北 衡水 053000

0 引言

随着工业4.0战略的推出，对弧焊机器人焊接作业的自动化和智能化提出了更高的要求［1］。在焊接作业中，焊枪与焊接工件的碰撞、编程精度不精确等问题时有发生，严重影响焊接质量和生产效率，因此需要采用虚拟仿真技术在焊前模拟机器人运动状态，以实现安全可靠的焊接工作［2-4］。

然而基于不同平台开发的仿真环境，会影响仿真的效果以及后续针对弧焊机器人通信接口的开发。朱智伟等［5］使用MATLAB工具箱对KUKA机器人进行了轨迹规划和运动学仿真，李双［6］和许琳娜［7］分别使用CAD软件SolidWorks和UG实现了工业机器人的加工仿真，WANG等［8］使用SolidWorks联合ADAMS对Delta并联机械臂进行了运动轨迹仿真，KUTS［9］使用Unity对工业机器人仿真和碰撞检测进行了研究。其中MATLAB模型渲染较差导致仿真效果不理想；而借助SolidWorks和UG平台或者成熟的三维引擎Unity设计机器人仿真虽然降低了开发难度，但是系统灵活性不足。

上述系统由于编程开发环境的限制，难以在仿真的基础上实现机器人的实时控制，离线编程后的机器人程序指令需要额外操作加载到机器人控制器中。而OpenGL作为一个跨平台、跨编程语言的专业图形接口，能够进行图形建模、几何变换、光照材质处理等［10］，满足构建焊接机器人虚拟场景和实现实时仿真效果的条件，同时便于后续开发机器人通信接口以实现对焊接机器人进行运动控制。

本文针对IRB2600机器人开发了一套机器人仿真及弧焊控制系统，机器人工作站由PC、IRC5控制器、机器人、MAG-350RPL焊接电源及焊枪组成，如图1所示。软件及应用程序通过Visual Studio的C#框架开发，包括运动学仿真、弧焊控制及路径规划三个模块，具有弧焊机器人运动学仿真及控制、相贯曲线焊缝的路径提取、数据的监测传输、焊接参数设定等功能，实现了机器人自动化和智能化焊接。

图1 机器人工作平台组成Fig.1 Composition of the robot station

1 焊接机器人运动仿真

焊接机器人运动仿真的实现需要结合机器人运动学和计算机图形学，对机器人进行DH参数建模以确定机械臂各关节的相对位置，依据DH参数求解正逆运动学方程，同时通过OpenGL对三维图形进行绘制、渲染和空间变换来搭建机器人仿真平台。

1.1 建立D-H模型

该焊接机器人为六自由度串联结构，可以由一系列关节连接的连杆来表述，将坐标系固连在每一个连杆上，通过齐次变换矩阵来描述这些关节之间的相对位置和方向［11-13］。使用MDH参数法为各个关节标定坐标系，以方便描述相邻连杆之间的相对转换关系。本文仿真对象为IRB2600焊接机器人，坐标系标定如图2所示，建立MDH参数如表1所示。其中，θ为关节角度，d为相邻关节距离，a为连杆长度，α为连杆扭角。

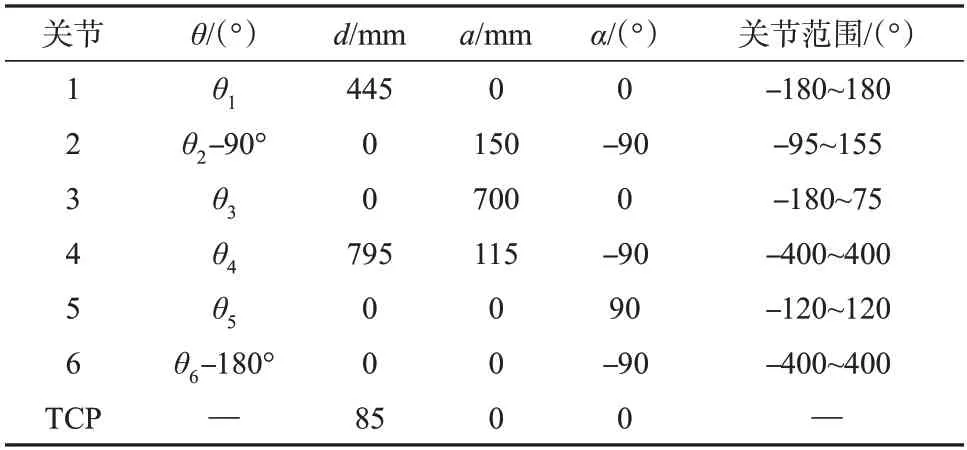
表1 IRB2600机器人DH参数Table 1 DH Parameters of the IRB2600 Robot

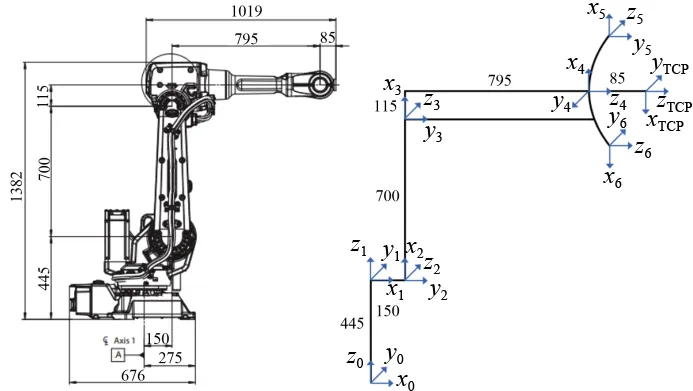
图2 机器人坐标系Fig.2 Robot coordinate system

1.2 正运动学求解

正运动学是在已知关节角度的条件下求解机器人末端位姿，通常选取齐次变换的方法求解。相邻连杆坐标系的齐次变换矩阵可表示为：

MDH参数标定后，根据式（1）得到机器人相邻两杆之间的位姿变换矩阵01T、12T、23T、34T、45T、56T。焊接机器人末端相对于基座坐标系的变换可由以下六个齐次变换矩阵连乘得到的位姿矩阵06T表示。其中n、o、a三个矢量组成的旋转矩阵表示机器人腕部的姿态，wx、wy、wz表示机器人腕部相对于基座的位置。

式中si表示sinθi；ci表示cosθi；下文中相同符号代表相同含义。

1.3 逆运动学求解

以上讨论了焊接机器人的正运动学方程，在已知各关节变量θ值时求解世界坐标系下工具末端的位置和姿态。而运动学逆解则是在给定机器人末端位姿的条件下，求解机器人各连杆之间的关节变量θ值，是进行焊接机器人轨迹规划的基础。

逆运动学求解常见的方法有几何法、解析法、数值法等［14］。其中几何法出现最早，但是对于多自由度的机器人实用性较差；数值法适用于动态的运动学逆解，但是在特殊点存在无法收敛的问题；相较于几何法和数值法，解析法求逆解运算方便且适用于多自由度机器人，常用于六轴工业机器人的运动学逆解［15-17］。因此，本研究采用解析法［18］对机器人进行逆运动学求解。前三个关节角通过wx、wy、wz直接求解，然后通过式（3）左右两侧元素两两相等来求解后三个关节角。

机器人各关节的表达式为：

使用MATLAB编写运动学程序，任意给出一组关节角度（25°、3°、10°、-45°、-10°、120°）求解正运动学，再将正运动学求得的位姿矩阵带入逆运动学方程中求得八组关节角度，如表2所示。其中第一组解和求解正运动学输入的关节角度对应，将求解的八组逆解反向带入正解方程也能得到与输入原关节角度一致的位姿矩阵。通过离线编程软件Ro-botStudio也可以对逆运动学方程进行验证，ABB机器人采用四元数来表示末端工具的姿态，使用轴配置（cf1，cf4，cf6，cfx）来确定机器人运动过程中的唯一姿态，其中cfx1～cfx7八种配置分别对应机器人的八组逆解。经检验求得的八组逆解与RobotStudio输入相同关节角度得到的八种配置对应的解完全一致，验证了逆运动学方程的准确性。

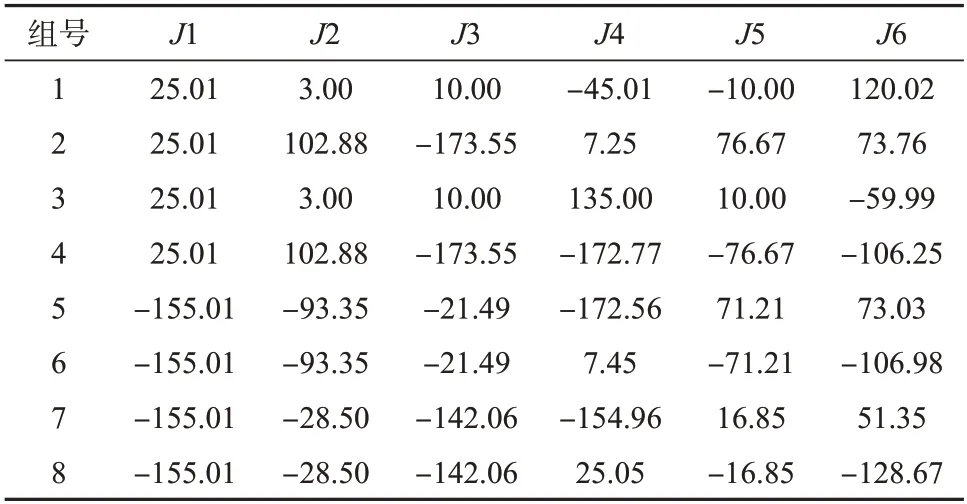
表2 运动学逆解Table 2 Inverse kinematics of robot

1.4 OpenGL机器人模型导入

OpenGL作为一个开放的图形API，可以在Visual Studio中搭建应用程序框架，它提供了模型绘制、几何与投影变换、光照材质和纹理颜色的渲染等功能，常用于工业仿真和虚拟现实技术［19-20］。

SolidWorks绘制的焊接机器人各关节零部件及坐标系标定如图3所示，将三维模型按标定坐标系输出保存为STL格式然后在OpenGL中加载。其中STL文件的图形由一系列的三角面片构成，通过三角面片的法矢量和三个顶点坐标完全定义［21］。每个三角面片都由四个向量组成，第一个向量表示三角形面的法线方向，后三个向量分别表示三个顶点的坐标。逐行解析读取STL文件信息并用OpenGL在仿真环境中依据D-H参数进行绘制。通过投影变换和视点变换将装配好的机器人显示在屏幕中央，在OpenGL中对机器人进行渲染，调节光照、材质和颜色等参数，最终实现焊接机器人可视化。

图3 机器人零部件模型Fig.3 Parts model of robot

1.5 仿真模块的搭建

将焊接机器人在虚拟空间可视化后，结合机器人运动学通过几何变换实现机器人的运动学仿真。最终搭建的焊接机器人仿真系统如图4所示，通过角度滑块对机器人各轴进行运动控制，同时实现焊枪末端位姿的实时显示，能够进行对正逆运动学方程的仿真验证。为了便于观测仿真模块还能切换视图方向以及对视图进行缩放。

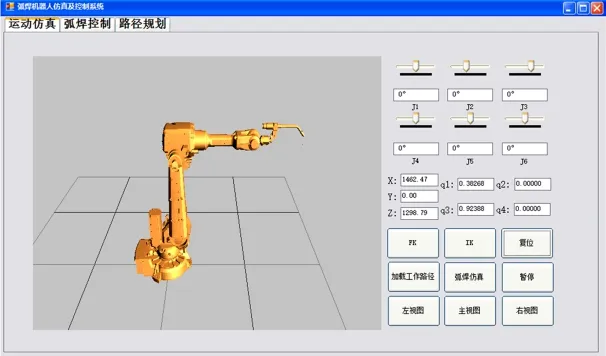
图4 弧焊仿真系统Fig.4 Simulation system of welding robot

2 焊接机器人控制系统设计

2.1 弧焊控制系统设计

该弧焊控制模块使用ABB机器人的PC SDK接口对IRC5控制器开发，具有网络连接、弧焊控制和状态监控功能。网络连接能够扫描并连接机器人控制器，获得对弧焊机器人控制器的控制权限。弧焊控制通过I/O信号对弧焊工艺信号进行控制，以调节焊接的电流电压参数和送丝送气等功能，同时能够控制机器人焊接过程的启停。状态监测则是在网络上连接控制器后实时将机器人的运动状态和日志信息反馈至应用程序界面。

PC SDK的类库包括的功能域如图5所示，这些用于访问控制器各种功能的类构成Controller API，是对机器人控制器进行二次开发的基础，通过对各功能类和派生类进行逐级访问来实现弧焊控制模块对控制器的检测和控制。

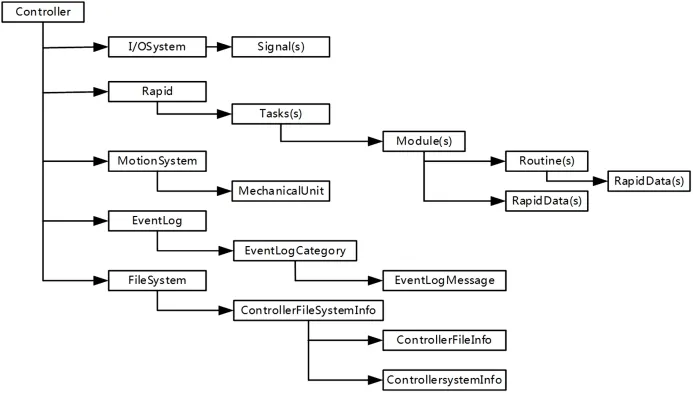
图5 PC SDK功能域Fig.5 Functional domains of PC SDK

2.2 弧焊控制系统的实现

弧焊控制系统如图6所示，集成了控制器连接、运动状态和日志监测、弧焊控制功能。控制系统使用离线编程软件RobotStudio进行实验验证。

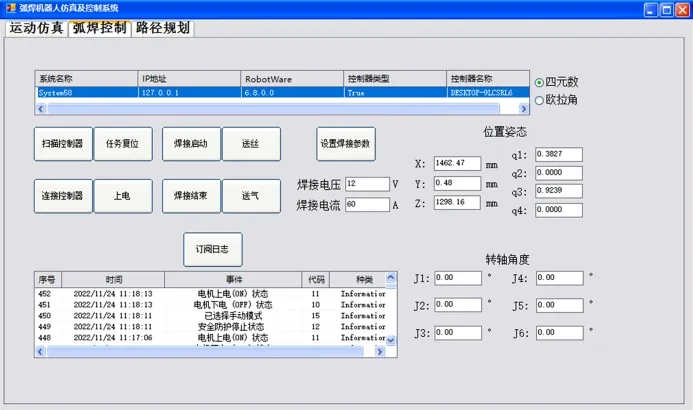
图6 弧焊控制系统Fig.6 Arc welding control system

使用时首先点击“扫描控制器”按钮搜索局域网内的所有在线机器人控制器，将机器人控制器的名称和类型、IP地址、版本等显示在控制系统面板上，然后选中所需的控制器进行连接并确认，弧焊控制系统即可获得机器人控制器的权限。

成功连接机器人控制器后，机器人运动状态和日志信息通过该系统来实时监测。机器人的运动状态信息包括焊枪末端的位置和姿态以及各关节的转轴角度，其中姿态能够以四元数或欧拉角的任意状态显示。控制器的日志信息记录了用户的操作记录和当前控制器状态。

弧焊控制包括弧焊参数调节、焊接启停控制、送丝送气控制。通过“设置焊接参数”按钮将文本框中的参数赋值给机器人控制器对应的弧焊信号。编辑好焊接任务程序并在焊接机器人电机上电后，点击“焊接启动”按钮即可开始焊接任务。

3 相贯曲线路径规划

3.1 焊缝位姿提取

在焊接机器人作业中，管-管相贯曲线焊缝的路径位姿复杂，焊缝路径规划对焊接质量影响较大。因此针对该空间曲线焊缝建立数学模型，以提取焊缝离散点的位姿，实现该系统的自动化路径。

相贯线模型如图7所示，建立参数方程为：

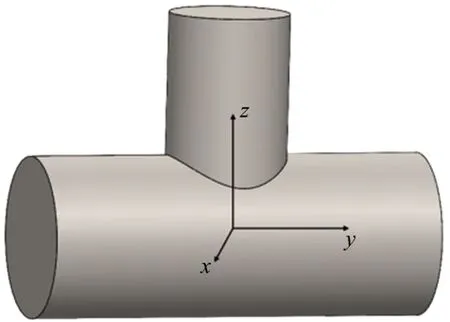
图7 相贯线数学模型Fig.7 Mathematical model of intersection curve

式中 两管轴线交点作为焊接机器人工件坐标系原点，R为主管半径，r为支管半径。将相贯曲线焊缝平均离散为n个点，则圆周角度，可以求得相贯曲线焊缝离散点的坐标值为：

由前面的正运动学可知，焊枪的姿态可以由旋转矩阵表示，其中向量=（nx，ny，nz）代表焊枪行走角，即空间曲线焊缝的切线方向。=（ax，ay，az）代表工作角，为焊缝法平面和主支管相交两曲线在该点切线的角平分线。=（ox，oy，oz）则代表焊枪自转角。

随机取焊缝的任意一离散点P（x0，y0，z0），θ0对应P点，则该点处的切向量为：

在点P处与切向量垂直的焊缝法平面方程为：

法平面和主管与支管相交得到两条曲线，在P点处对两条曲线求导分别得到两条切线的方向向量和，然后取两切线的角平分线，求得表示焊枪工作角的向量为：

向量n和向量a求解后，向量o可以通过右手定则确定，即

通过建立相贯线模型得到焊枪的位姿矩阵后，使用MATLAB拟合代表相贯曲线焊接过程中焊枪工作角的向量如图8所示，可以看出建立的相贯曲线参数方程有效可靠，能够实现理想的焊枪角度。最终得到的相贯线焊缝特征坐标系如图9所示，焊枪在各离散点的位置和姿态可以通过该特征坐标系确定。

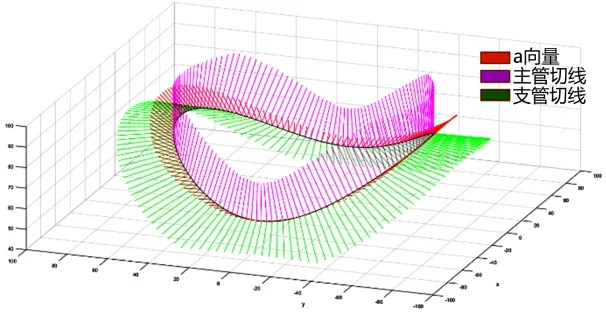
图8 焊枪工作角Fig.8 Working angle of welding gun

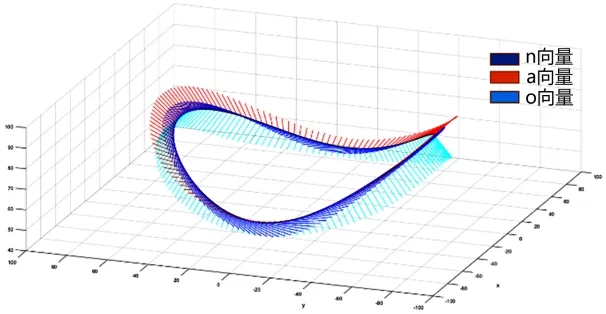
图9 焊缝特征坐标系Fig.9 Welding seam’s characteristic coordinate system

3.2 路径规划模块的实现

通过建立相贯线的数学模型，提取相贯曲线焊接路径离散点的位姿。依据建立的位姿方程开发路径规划模块如图10所示，首先输入主管和支管的半径，提取的各离散点位姿数据即显示在TextBox中。将焊接机器人的位姿数据转换为机器人可识别的RAPID语言，再通过开发的应用程序将机器人程序文件直接加载至虚拟机器人控制器中，使用弧焊控制系统进行调试仿真，如图11所示。

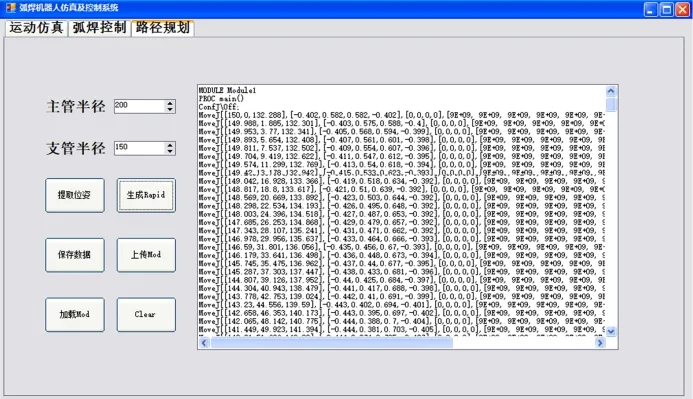
图10 路径规划模块Fig.10 Path Planning module

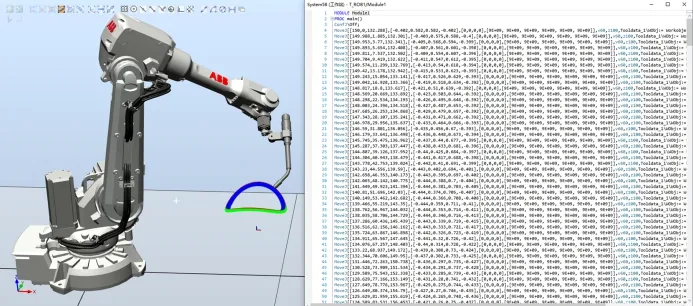
图11 加载程序进行仿真调试Fig.11 Load the program into the virtual controlle

其中焊缝离散点位姿转换成机器人语言的关键是姿态四元数的转换，位置、相对坐标系、速度等都是基于文本的转换，其中轴配置选项关闭，使机器人自动匹配合适的轴配置来到达目标点。在将表示机器人焊枪姿态的旋转矩阵转换为四元数时，需要先判断出四元数中的最大值，再以该值依次计算出另外三个元素，以保证数值结果的稳定性。

4 结论

（1）本文采用DH参数法建模并求解机器人运动学方程，并基于OpenGL搭建了弧焊机器人仿真环境。经MATLAB与RobotStudio测试证明对机器人的运动学分析准确可靠，满足机器人运动学仿真的需求，且能够达到机器人工作的仿真效果，为进一步焊接过程的轨迹规划奠定了基础。利用PC SDK在仿真平台的基础上开发了机器人弧焊控制系统，经测试PC能够作为上位机对机器人控制器进行实时监视和控制。然后通过建立相贯线位姿数学模型解决了其复杂空间曲线的路径规划问题，经MATLAB验证表明求取的机器人焊枪工作角度合理，提高了编程效率，实现了焊接工作的自动化和智能化。

（2）本文的路径规划模块仅仅针对单一焊接结构件，后续还需完善自动路径规划功能，如通过三维射线拾取或视觉特征识别来提取工件轨迹，以适配更加广泛的焊接任务。