可调整焊枪姿态直线摆弧路径算法研究*

潘海鸿，尹华壬，梁旭斌，李睿亮，夏 凯，陈琳

(广西大学 机械工程学院，南宁 530004)

0 引言

目前工业制造的焊接机器人作为应用最广泛的一类工业机器人[1]，在各国机器人应用比例中大约占总数40%～60%，具有巨大市场需求。对于焊接机器人而言，尤其是弧焊机器人在焊接作业中不仅需具有一般的直线圆弧等运动功能，还需具备摆弧焊接功能[2]。国外OTC和FANUC机器人控制系统具有一次函数、三角函数以及圆弧摆弧焊接方式并可调节摆动频率、振幅以及停止时间等。国内杨海涛[3]、邬亚兰[4]、刘越[5]等学者研究基于正弦波形式摆动的空间直线与圆弧路径插补算法。

在实际焊接过程中，焊缝倾角、焊缝转角、焊枪工作角以及焊枪行走角[6]影响着焊缝成型质量好坏，其中焊缝倾角、焊缝转角决定焊缝在空间中的位姿，焊枪工作角以及焊枪行走角决定焊接过程中焊枪姿态。在某些情况下，如焊接工件之间出现不等厚情况时，需改变焊枪工作角使焊枪贴近板厚焊件，使厚焊件与熔池接触面积增大；此外根据实际焊接情况有时需调整焊枪行走角，即要求焊枪与焊缝法平面形成向前倾角[7]，通过使焊枪在焊接过程中前倾或后倾改变所形成焊缝成形厚度与宽度[8]。传统示教不能适应实际焊接过程中焊接参数需随时调整的现象，为解决每进行一次焊接工艺参数调整均需要重新示教将增加编程时间致使工作效率低的难题，故提出一种可调整焊枪姿态的直线摆弧路径算法，可在一次示教后实现不同焊枪姿态焊接并调整焊接工艺达到快速调试效果[9-10]。

1 焊缝与焊枪的位姿描述

如图1所示为焊接位姿示意图。在实际焊接过程中焊接工件与焊枪复杂多变，为方便对焊接位姿进行表述，使用焊枪轴线表示焊枪并对焊缝倾角、焊缝转角、焊枪工作角以及焊枪行走角等与焊缝和焊枪位姿相关描述内容作出定义：

图1 焊接位姿示意图

焊缝中心线：焊根与盖面层中心连线。

焊缝转角：焊缝中心线与重力反方向线在焊缝法平面上投影所形成角度。可用θ表示，其范围为0°～180°。

焊缝倾角：焊缝轴线行进方向与水平面之间的夹角。可用φ表示，若为上坡焊φ则大于0，下坡焊φ小于0，其范围为-90°～90°。

焊枪工作角：焊枪轴线与焊缝中心线在焊缝法平面投影所成夹角。可用α表示，若焊枪轴线在焊缝中心线上方为负值，在焊缝中心线下方为正值。

焊枪行走角：焊枪轴线与焊缝法平面所成夹角。可用β表示，前倾焊时β取正值，后倾焊时时β取负值。

2 可调整焊枪姿态摆弧路径生成算法

设用户通过示教获取焊缝起点O1=(x1,y1,z1)，焊缝终点O2=(x2,y2,z2)，平面1上随意一点S1=(xs1,ys1,zs1)以及平面2上随意一点S2=(xs2,ys2,zs2)，焊枪摆动幅值大小为AMP，摆周期为ts，机器人末端位移线速度为v。由示教点得到焊接平面与工件位置关系如图2、图3所示，加入焊枪工作角与焊枪行走角后焊接平面与工件位置关系如图4、图5所示，其中l0：焊枪轴线。l1：焊枪轴线在焊缝法平面的投影。l2：焊缝中心线。其算法实现过程如下：

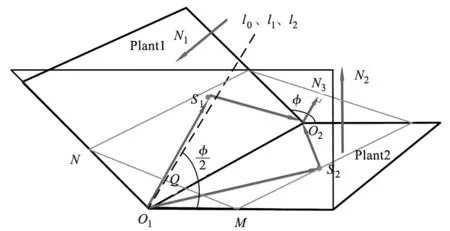
图2 焊接平面与工件位置关系空间示意图

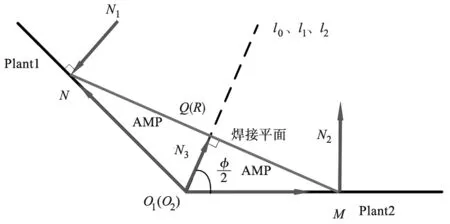
图3 焊接平面与工件位置关系平面示意图

图4 焊枪姿态调整后焊接平面与工件位置关系空间示意图

图5 焊枪姿态调整后焊接平面与工件位置关系平面示意图

(1)对输入的点进行共线判断。在示教获取输入点时，若出现平面参考点与示教起点或终点共线则无法构成平面的情况，此时需分别对两平面参考点与焊缝起点与终点进行共线判断。O1、O2、S1三点以及O1、O2、S2三点不共线的充分条件为：

(1)

(2)

(2)确定两工件加工平面夹角φ。由图2几何关系可知：

(3)

其中，N1、N2分别为平面1与平面2的法向量，取Z坐标较小的作为基准参考面2，其中N1=O1S1×S1O2、N2=O1S2×S2O2。

(4)确定焊接平面与平面1夹角∠O1N′M′。 由图5中所示图形关系可得：

(4)

(5)确定平面2内垂直于焊缝轴线单位向量EO1M′。

(5)

(6)确定加入焊枪姿态调整后焊接平面上的点M′。

M′=O1+O1M′×EO1M′

(6)

(7)确定焊缝至焊接平面单位偏移矢量EO1Q′

(7)

其中，O1N′=O1N′×EO1N′，由图5中几何关系可得O1N′长度，

(8)

(9)建立焊枪末端坐标系OtXtYtZt如图6所示，求出各轴在机器人绝对坐标系下方向余弦值。取焊枪轴线作为焊枪坐标系Zt轴，方向由焊枪指向焊缝；在机器人原点时刻焊枪坐标系Yt轴相对于绝对坐标系Yw轴方向相反，其世界坐标系下余弦值为(0,-1,0)，在焊接起点处以焊缝轴线计算焊枪坐标系Yt轴，因此有：

Zt=-EO1Q′=(axt,ayt,azt)

(9)

图6 焊枪末端坐标系OtXtYtZt与机器人绝对坐标系关系示意图

焊枪坐标系Xt轴在机器人绝对坐标系下余弦值Xt=Yt×Zt=(nxt,nyt,nzt)。

(10) 根据焊枪坐标系相对于机器人绝对坐标系各轴方向余弦值建立机器人位于焊接平面上焊接起点Q′位姿矩阵MSR、焊接平面上一点M′位姿矩阵MMR、焊接平面上焊接终点R′位姿矩阵MER。

(10)

(11)

(12)

(11) 为改变焊枪行走角后焊接起点仍位于焊接平面上故将焊缝平移至焊接平面后再加入焊枪行走角β处理，如图7所示，加入焊枪行走角可视为焊枪坐标系绕自身坐标系Xt转过β度，由此易得加入焊枪行走角后焊枪姿态变化矩阵Tb。

(13)

图7 加入焊枪行走角后焊枪姿态示意图

(12) 确定经焊枪行走角偏移后焊接平面上焊接起点Q′位姿矩阵MSR′、焊接平面上一点M′位姿矩阵MMR′、焊接平面上焊接终点R′位姿矩阵MER′。

MSR′ =MSR·Tb

(14)

MMR′ =MMR·Tb

(15)

MER′ =MER·Tb

(16)

(13)以O1′ = (xo1,yo1,zo1)作为直线起点,O2′ = (xo2,yo2,zo2)作为直线终点，由直线摆弧算法得到沿焊缝方向单位插补向量VctWeld和沿摆动振幅方向的向量Yi。则焊接平面上经摆弧偏移后第i个插补点在机器人绝对坐标系下位置量Posi=O1′ +i·VctWeld+Yi= (xi,yi,zi) ，将位姿矩阵MSR′ 、MMR′ 或MER′ 中姿态矩阵通过欧拉角变化求出矩阵中对应的欧拉角值a、b、c，最后可计算得新焊接平面上各插补点机器人位姿值Posorii=(xi,yi,zi,a,b,c) 。

3 算法仿真

从空间中获取点P1、P2、P3、P4分别令P1为焊缝起点,O1、P2为焊缝终点O2、P3为工件1表面上一点S1、P4为工件2表面上一点S2。设P1=(10.000, -50.000, 10.000)、P2=(10.000, 50.000, 10.000)、P3=(10.000, 4.000, 20.000)、P4=(20.000, 6.000, 10.000)焊枪摆动幅值AMP=2，在焊枪工作角与行走角均为0°的条件下，所生成摆弧路径插补点如图8所示由粉色圆点所构成，在焊枪工作角为-30.000°，行走角为45.000°条件下其摆弧路径插补点如图8所示由蓝色星号点所构成。Q为未加入焊枪姿态调整前焊接起点、Q′为加入焊枪姿态调整后焊接起点位置。

图8 调整焊枪姿态前后直线摆弧路径仿真

在焊接平面上Q点建立焊枪工作角与行走角为0°时焊枪坐标系Q1TX1TY1TZ1T,在焊接平面上Q′点建立焊枪工作角-30.000°，焊枪行走角为0°时焊枪坐标系Q2TX2TY2TZ2T，以及焊枪工作角-30.000°，行走角为45.000°时焊枪坐标系Q3TX3TY3TZ3T。坐标系Q1TX1TY1TZ1T与Q2TX2TY2TZ2T如图9所示，Q1TX1TY1TZ1T与Q2TX2TY2TZ2T以及Q3TX3TY3TZ3T如图10所示。通过路径生成算法可得各坐标系中各个轴在机器人绝对坐标系下余弦值，其中，

X1T=(-0.707,0.000,0.707)，Y1T=(0.000,1.000,0.000)，Z1T=(-0.707,0.000,-0.707);

X2T=(-0.966,0.000,0.259)，Y2T=(0.000,1.000,0.000)，Z2T=(-0.259,0.000,-0.966)；

X3T=(-0.966,0.000,0.259)，Y3T=(0.183,0.707,0.683))，Z3T=(-0.183,0.707,-0.683)；

图9 调整焊枪工作角前后焊枪坐标系

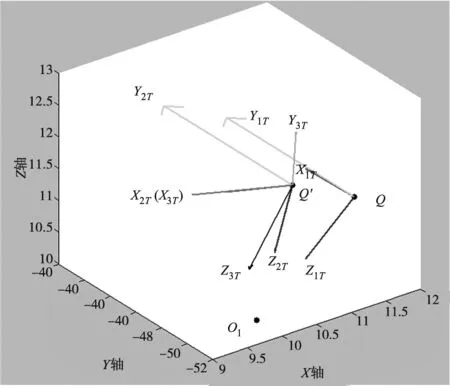
图10 调整焊枪工作角与行走角前后焊枪坐标系

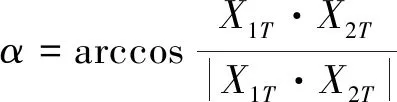
4 实验与分析

为验证改变焊枪工作角与行走角直线摆弧路径生成算法的有效性，在相同材料以及相同焊接参数前提下进行焊接实验，对比观察焊枪工作角与行走角调整前后的焊接效果图来验证。

焊接实验平台主要由：机器人本体(送丝机、焊枪)、电气控制柜(伺服驱动器、运动控制器、工控机)、示教器、数字焊机组成，如图11所示，焊接实验采用T型接头工件，工件材料为Q235，板厚3mm。

图11 弧焊机器人焊接实验平台

实验中设置焊接电流为140A，焊接电压为19V，机器人末端运动线速度为7mm/s。将焊缝分成两段示教，其中一段设定焊枪工作角与行走角为0°，则焊接过程中焊枪轴线与焊缝中心线共线；另一段路径设定焊枪工作角为-15°，行走角为40°，进行焊接实验，焊接结果如图12、图13所示。

图12 焊枪姿态调整前后焊接对比主视图

图13 焊枪姿态调整前后焊接对比侧视图

通过对图12观察可知，在焊枪工作角与行走角均为0°条件下进行焊接的两平面上焊趾至焊缝轴线距离基本一致，而在加入-15°工作角后因焊枪轴线向另一平面靠近因此使熔池更多落在靠近焊枪轴线平面上；通过图13对比可发现，未加焊枪行走角前焊缝具有一定凸度。在加入焊枪行走角后变为前倾焊，前倾焊将使电弧力对熔池液体向后排作用力减少，使熔池底部金属液体变厚从而阻碍电弧对熔池底部母材加热，电弧对熔池前部未熔化母材预热作用加强，因此焊缝宽度增加，余高减小形成一定凹度。

5 结论

弧焊机器人焊枪姿态快速调整在机器人焊接作业中起着不可或缺的作用，在焊缝与焊枪的位姿模型基础上提出一种可调整焊枪姿态的直线摆弧路径算法。仿真实验证实：与传统示教不能适应实际焊接过程中焊接参数需随时调整的现象相比，所提出的可调整焊枪姿态的直线摆弧路径算法可在一次示教后实现不同焊枪姿态焊接并调整焊接工艺达到快速调试效果，证明了所提出方法的有效性。