非奇异M-矩阵的性质

钟 琴

(四川大学锦江学院 数学教学部, 四川 眉山 620860)

1 记号

M-矩阵是计算数学及相关领域具有广泛应用背景的重要矩阵类.M-矩阵起源于解某类微分方程的数值解(例如偏微分方程中的有限元方法).经济价值模型矩阵和反网络分析的系数矩阵也和M-矩阵密切相关, 许多学者对M-矩阵进行了广泛地研究, Plemmons[1]列出了40个和M-矩阵等价的条件,Berman等[2]进一步扩充为50条,另外还有许多关于M-矩阵及其应用的研究[3-11].本文在现有结果的基础上,对非奇异M-矩阵的性质做进一步的研究.

首先给出相关概念和定义.

记N={1,2,…,n},Rn×n(Cn×n)表示n阶实(复)矩阵的集合.

定义1[1]设A=(aij)∈Rn×n, 若矩阵A的所有元素aij≥0, 则称矩阵A为非负矩阵,记为A≥0, 用ρ(A)表示非负矩阵A的谱半径.

记Zn×n={A=(aij)∈Rn×n|aij≤0,1≤i,j≤n,i≠j}.

定义2[3]若A∈Zn×n, 且A-1≥0, 则称A为非奇异M-矩阵.

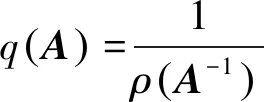
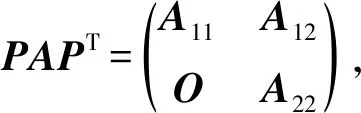
定义5[3]若A是不可约非负矩阵(或不可约M-矩阵),则存在正向量u,使得Au=ρ(A)u(或Au=q(A)u), 其中u称为A的右Perron特征向量.

2 主要结果

下面给出相关引理.

引理1[6]设A=(aij)∈Rn×n为非负不可约矩阵,并且有n维正向量x,使得Ax≤αx对某一α∈R成立, 则ρ(A)≤α.

引理2[7]设A=(aij)∈Rn×n为非负矩阵,则A不可约的充要条件是ρ(A)为A的单重特征值,且A与AT相应于ρ(A)的特征向量皆正.

引理3[7](Gerschgorin圆盘定理) 设A=(aij)∈Cn×n, 则A的所有特征值包含在如下n个圆盘的并之中:

引理4[7](Hölder不等式) 设y=(y1,…,yn)T∈Rn,z=(z1,…,zn)T∈Rn为非负向量,0<α<1,则

引理5[9]设A=(aij)∈Rn×n为非奇异M-矩阵,则q(A)≤aii,i∈N.

下面给出本文关于非奇异M-矩阵及非奇异M-矩阵最小特征值的相关性质.

定理1设A=(aij)∈Rn×n为非奇异M-矩阵,n维非负非零向量x满足Ax≤αx对某一α∈R成立,则q(A)≤α.

证明记A=sI-B,s>ρ(B),B=sI-A≥0,ρ(B)=s-q(A),令ε>0,构造矩阵B(ε)=(bij+ε)n×n, 则B(ε)>0,BT(ε)>0, 故BT(ε)有正向量y(ε),使得

BT(ε)y(ε)=ρ(BT(ε))y(ε)

注意到ρ(BT(ε))=ρ(B(ε)), 则有

yT(ε)B(ε)=ρ(B(ε))yT(ε)

(1)

又由Ax≤αx, 知-Ax≥-αx,进一步有(sI-A)x≥(s-α)x,也即Bx≥(s-α)x.

因为

B(ε)x-(s-α)x>Bx-(s-α)x≥0

所以

B(ε)x-(s-α)x>0

上式两边同时左乘yT(ε), 再结合式(1)得

注意到yT(ε)x>0, 可知对任意ε>0有

ρ(B(ε))-(s-α)>0

进一步得

另一方面,ρ(B)=s-q(A), 因此q(A)≤α.

推论1设A=(aij)∈Rn×n为非奇异M-矩阵,n维非负非零向量x满足Ax≥βx对某一β∈R成立, 则q(A)≥β.

定理2设A=(aij)∈Rn×n为非奇异M-矩阵,n维非负非零向量x满足βx≤Ax≤αx对某α,β∈R成立, 则β≤q(A)≤α.

定理3设A=(aij)∈Rn×n为非奇异M-矩阵,则A不可约的充要条件是q(A)为A的单重特征值,且A与AT相应于q(A)的特征向量皆正.

证明记A=sI-B,s>ρ(B),B=sI-A≥0, 由A不可约可知B也不可约,根据引理2得q(A)=s-ρ(B)为A的单重特征值, 且B与BT相应于ρ(B)的特征向量皆正,由A与B的关系可知A与AT相应于q(A)的特征向量也皆正.

定理4设A=(aij)∈Rn×n为不可约非奇异M-矩阵, 则A不能有两个线性无关的非负特征向量.

证明因为A是不可约的M-矩阵, 故设x=(x1,x2,…,xn)T>0是A对应于q(A)的特征向量, 此外假设y=(y1,y2,…,yn)T≥0且y≠0是A对应于α的特征向量, 且x与y线性无关.由定理3知,q(A)为A的单重特征值, 故α≠q(A).进一步记z=(z1,z2,…,zn)T为AT相应于q(AT)=q(A)的正特征向量,于是有

q(A)(y,z)=(y,q(A)z)=(y,ATz)=

zTAy=(Ay,z)=(αy,z)=α(y,z)

注意到α≠q(A), 故必有(y,z)=0, 这与y≥0,z>0且y≠0时(y,z)>0矛盾, 这就证明了y是不存在的,故A不能有两个线性无关的非负特征向量.

注1当A为可约非奇异M-矩阵时定理4未必成立.例如, 考虑如下的可约M-矩阵

非负向量x=(1,0,0)T及y=(0,1,0)T均为特征值2的特征向量, 并且x和y线性无关.

定理5设A=(aij)∈Rn×n为非奇异M-矩阵, 向量v=(v1,…,vn)T>0,0≤α≤1.记

则

证明当α=0和α=1时, 由Gerschgorin圆盘定理易得结论成立. 故设0<α<1. 构造矩阵V=diag(v1,…,vn),因为v=(v1,…,vn)T>0,所以V可逆. 记

由引理5知λ≤att,t∈N,从而有

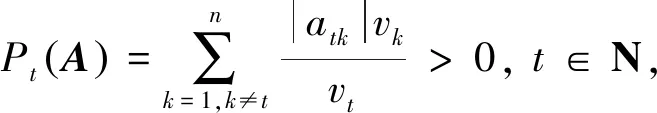
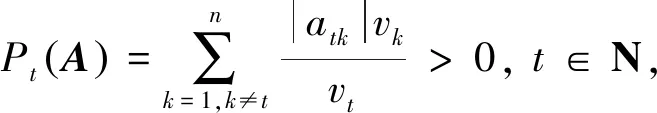
所以

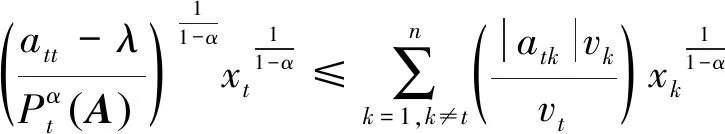
(2)

式(2)两边同时对t求和得

(3)

假设对满足xt≠0的所有t都有

则与式(3)矛盾. 因此, 至少有一满足xt≠0的t使得

也即

从而

进一步有

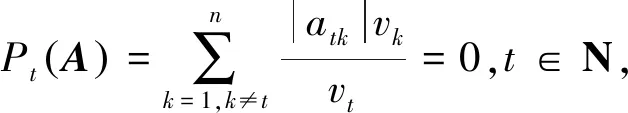
(4)

式中

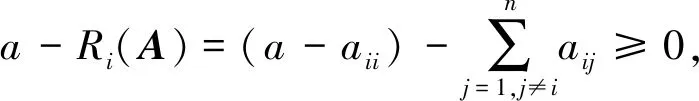
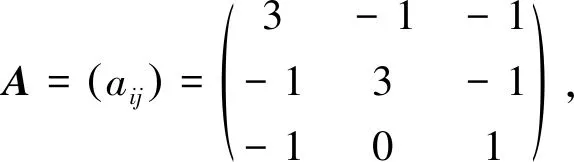
可得q(A)≥0.267 9,利用本文推论2可得q(A)≥0.333 3(α=1).

可得q(B)≥0.438 4,利用本文推论2可得q(B)≥0.500 0(α=1).

和文献[8]的估计结果相比, 虽然非奇异M-矩阵最小特征值的下界没有得到改进, 但是从计算量上看, 文献[8]的估计式需要计算非奇异M-矩阵的逆矩阵, 计算量较大, 本文推论2的结果只需根据非奇异M-矩阵自身的元素即可计算出最小特征值的下界.

3 结论

本文利用非负矩阵与M-矩阵的关系, 给出了M-矩阵的特征向量和最小特征值以及非奇异M-矩阵的相关性质, 并且结合Gerschgorin圆盘定理和Hölder不等式给出了非奇异M-矩阵最小特征值的下界估计式.

致谢:本文得到四川大学锦江学院教改项目应用型大学《线性代数》课程教学设计的研究与实践(2023JG013)的资助,在此表示感谢.