四阶非线性分数阶反应扩散方程的混合有限元方法
覃 燕 梅
(内江师范学院 数学与信息科学学院, 四川 内江 641100)
0 引言
近年来,分数阶偏微分方程因其在物理、化学、生物和工程等各个领域的频繁出现而成为研究的焦点[1-5]. 四阶分数阶反应扩散方程是一类重要的四阶分数阶偏微分方程模型,经常出现在许多科学领域,如:反应扩散行波问题系统,液晶中畴壁的传播和双稳态系统的模式形成等[6-10]. 本文将研究如下四阶非线性分数阶反应扩散方程:
(1)
其中Ω⊂R2,J=(0,T]分别表示空间区域和时间区域,且Ω是一个有界凸多边形区域,边界为∂Ω,反应项f(u)是关于u的非线性函数,且满足|f(u)|≤C|u|和|f′(u)|≤C(C>0为常数),初始值u0(x)和g(x,t)为已知函数,且Riemann-Liouville(R-L)分数阶导数定义为

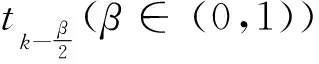
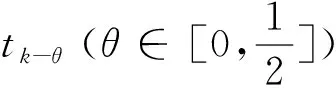
本文结构安排如下:第1节,推导出含参数θ的二阶混合有限元格式;第2节,导出该格式的无条件稳定性;第3节,对该格式的先验误差进行详细分析,并证明误差结果在时间上可达到二阶精度.
1 含参数θ的二阶混合有限元格式
为了给出全离散格式,在时间区间[0,T]上插入节点:tn=nΔt(n=0,1,2,…,N),对于任意正整数N,步长Δt=T/N,tn满足0=t0 引理1[16]若 在tn-θ时刻,存在如下二阶逼近: (2) 其中 (3) f(tn-θ)=(1-θ)fn+θfn-1+O(Δt2) (4) g(v(tn-θ))= (5) (6) 其中 (7) 而 (8) 引理5[15-17]设{ϖγ(i)}如式(7)所定义,则对任意实向量(v0,v1,…,vL)∈RL+1和正整数L,有 (9) 成立. 为了形成混合有限元算法,引入辅助变量σ=Δu,可将原问题(1)改下为如下耦合系统: (10) 当n=1时, (11) 当n≥2时, (12) 其中 (13) (14) (15) 注2文献[10,15]所研究的方法仅仅针对f(u)=γu(γ为常数)进行了讨论,而本文针对f(u)为u的非线性函数进行了讨论. 相比于文献[14]的双重有限元方法,本文所给的方法不需要在多重网格上进行计算. 该格式的稳定性和误差估计将在下面两节给出. 为了讨论的方便,本文用c表示与h和Δt无关的非负常数,且在不同的情况下表示不同的常数. (16) 其中 [χn]=(3-2θ)‖χn‖2-(1-2θ)‖χn-1‖2+ (17) 且 (18) (19) ∇∇ (20) 根据式(6)、Cauchy-Schwarz不等式、Young不等式和|f(u)|≤c|u|,可得 (21) (22) 和 (23) 将式(21)-(23)代入式(20)可得 ∇∇ (24) (25) 可得 (26) 用类似于n≥2的方法,可以得到 (27) 又因为 故进一步可得 ∇∇ (28) 将式(28)代入(24),并由式(9)可得 (29) 根据Gronwall不等式和引理6可得 (30) 即得到定理1的结论.证毕. 为了给出先验误差估计,引入投影和估计不等式. (∇v,∇φh)=(∇(Λhv),∇φh), ∀φh∈Vh, (31) 满足估计不等式 (32) 存在不依赖时空步长(h,Δt)的常数c,使得对n≥1,有 证明为了给出误差估计,引入记号 (33) 和 (34) 当n=1时, (35) 当n≥2时, (36) ∇∇ (37) ∇∇ (38) 根据式(6)、Cauchy-Schwarz不等式、Young不等式、|f(u)|≤c|u|和|f′(u)|≤c,可得 (39) (40) (41) 和 (42) 将式(39)-(42)代入式(38),可得 ∇∇ (43) (44) ∇∇ (45) 将式(45)代入式(43)可得 ∇∇ (46) 根据式(9)、(18)、(46)和Gronwall不等式,得 再结合三角不等式可得定理2.证毕. 本文基于θ格式结合分数阶导数的WSGD格式近似时间方向,并采用Galerkin有限元方法离散空间方向,针对四阶非线性分数阶反应扩散方程,建立了二阶混合有限元格式. 证明了该方法的无条件稳定性,给出了先验误差估计. 误差结果表明,本文所建立的格式在时间上可达到二阶精度.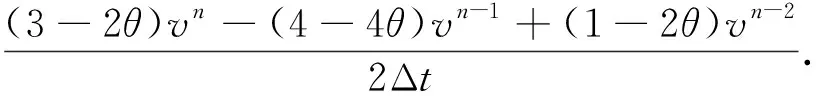
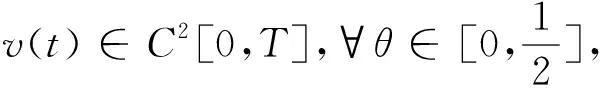
≜fn-θ+O(Δt2),
(2-θ)g(vn-1)-(1-θ)g(vn-2)+O(Δt2)
≜g[vn-θ]+O(Δt2).
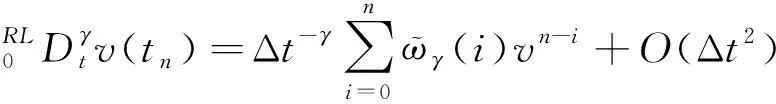



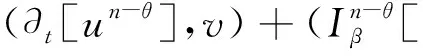
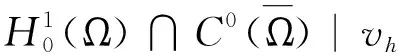
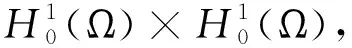

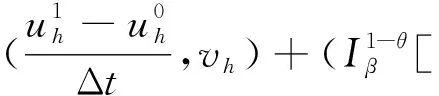

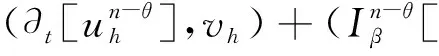
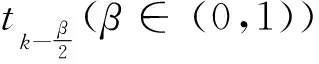
2 稳定性
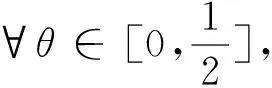
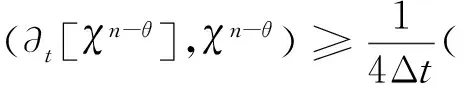
(2-θ)(1-2θ)‖χn-χn-1‖2,
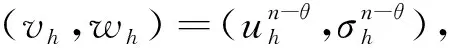
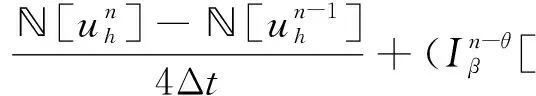
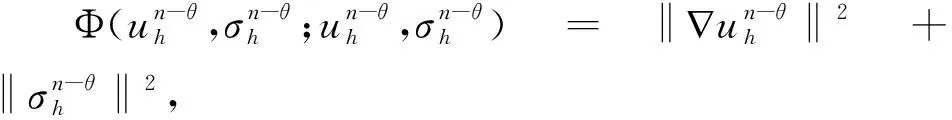
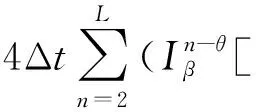


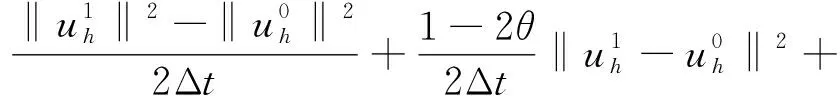


3 先验误差估计
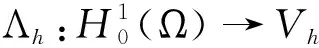


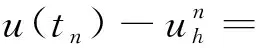






4 结语

