双定数混合截尾下Burr XII分布失效率和可靠度的贝叶斯估计
金雪莲, 李云飞
(西华师范大学 数学与信息学院, 四川 南充 637009)
0 引言
定数截尾试验是可靠性统计分析中一种重要的寿命试验方案.定数截尾试验方案是取n个产品,事先规定失效数r,截尾样本记为t1≤t2≤…≤tr.诸多学者对此试验方案进行了研究.龙兵等[1-2]研究了定数截尾试验下Lomax分布参数的估计问题;张春雨等[3]研究了在不同损失函数下Poisson-Lomax分布参数的Bayes估计;刘璐等[4]研究了Pareto分布参数的区间估计问题.龙兵等[5]提出了双定数混合截尾试验,即两个定数截尾试验的混合,双定数混合截尾试验与定数截尾试验相比,能更多了解产品的性能和提高产品的精度.
Burr XII分布由Burr[6]在1942年基于微分方程dF(x)/dx=F(x)(1-F(x))g(x,F(x))引入,在社会学、经济学等领域有着广泛的应用,国内外众多学者致力于研究此分布. Kohansal[7]研究了混合逐步截尾样本下Burr XII分布的Bayes估计和经典估计; Rania等[8]对Burr XII分布和Weibull分布的未知参数进行估计;周巧娟[9]研究了Burr XII分布参数θ的估计问题;周洁等[10]基于不同的损失函数对Burr XII分布参数θ的Bayes估计问题进行讨论;刘荣玄[11]基于逐次定数截尾样本,采用减函数法对Burr XII分布的失效率的Bayes估计进行了讨论;韦师等[12]结合复合LINEX对称损失函数,研究Burr XII分布的Bayes估计和E-Bayes估计;王雪琴等[13]研究了Burr Type XII分布参数θ的估计问题.然而在双定数混合截尾场合,研究Burr XII分布失效率和可靠度的Bayes估计的文献较少.因此,本文假设刻度参数已知,将基于双定数混合截尾试验对Burr XII分布失效率和可靠度的Bayes估计问题进行讨论.
Burr XII分布的分布函数和概率密度函数为:
F(x,α,θ)=1-(1+xα)-θ,
x>0,α>0,θ>0,
f(x,α,θ)=αθxα-1(1+xα)-(θ+1),
x>0,α>0,θ>0,
其中α为刻度参数,θ称为形状参数.
失效率和可靠度函数分别为:
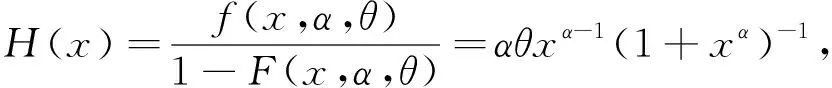
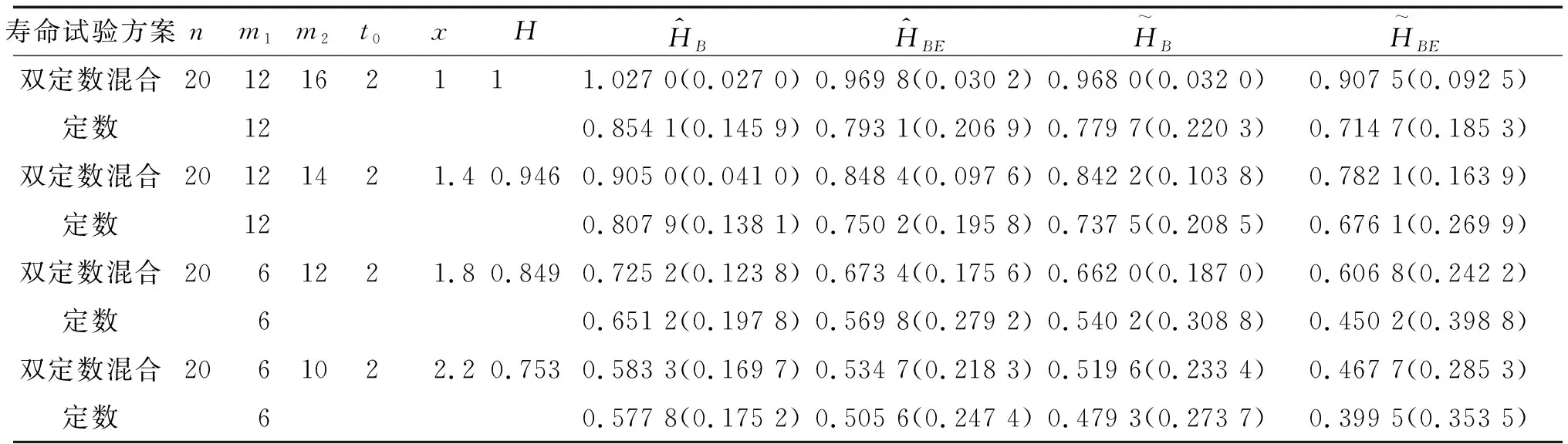
双定数混合截尾试验如下:假设随机抽取n个寿命独立同分布的样品进行试验,事先确定正实数t0以及正整数m1,m2,且满足m1 把上述两种情形分别表示为CaseI和CaseII,从而得到如下观测数据: 其中 设Burr XII分布的样本容量为n的双定数混合截尾样本为x*=(x1:n,x2:n,…,xk:n),则x*的似然函数为 (1) 取形状参数θ的先验分布为Ga(a,b),其概率密度函数为 (2) 由式(1)、(2),可得到θ的后验密度函数: 由于H(x)=αθxα-1(1+xα)-1,则 H>0,因此,H(x)的后验密度函数为 利用平方损失函数和熵损失函数的定义及计算公式[14-17],可得到如下定理. 定理1在平方损失函数L(H,δ)=(H-δ)2下,若形状参数θ的先验分布为π1(θ),则H(x)的Bayes估计为 证明在平方损失函数下,H(x)的Bayes估计为 证明在熵损失函数下,H(x)的Bayes估计为 由于可靠度R(x)=(1+xα)-θ=e-θln(1+xα),则可以得到可靠度R(x)的Bayes估计如下. 定理3在平方损失函数L(R,δ)=(R-δ)2下,若形状参数θ的先验分布为π1(θ),则R(x)的Bayes估计为 证明在平方损失函数下,R(x)的Bayes估计为 令[b+s+m+ln(1+xα)]θ=y,则上式为 证明在熵损失函数下,R(x)的Bayes估计为 θ>0. (3) 由式(1)、(3),可得到θ的后验密度函数为 即 θ>0. 根据先验分布π2(θ)可得如下定理. 定理5在平方损失函数L(H,δ)=(H-δ)2下,若形状参数θ的先验分布为π2(θ),则H(x)的Bayes估计为 定理7在平方损失函数L(R,δ)=(R-δ)2下,若形状参数θ的先验分布为π2(θ),则R(x)的Bayes估计为 定理5-8的证明过程在此省略. 类似文献[19]的方法,用随机模拟产生一个服从Burr XII分布的简单随机样本,步骤如下: (1)设均匀分布U(0,1)产生的相互独立随机样本为Y1,Y2,…,Yn. 其中一个样本按从小到大排列如下:0.368 2,0.513 9,0.556 1,0.587 3,0.734 2,0.844 3,0.904 8,0.920 6,1.243 6,1.259 8,1.321 2,1.355 7,1.399 3,1.399 5,1.454 5,1.562 0,1.831 2,2.232 7,2.307 9,4.152 1. 以上样本取不同的截尾数,可以计算出H(x)和R(x)在Gamma分布和Jeffreys先验分布下的Bayes估计以及各个估计的误差值(括号中),如表1和表2所示. 表1 失效率H(x)的估计 表2 可靠度R(x)的估计 由表1和表2可知: (1)在双定数混合截尾试验下,得到的失效率H(x)和可靠度R(x)估计值的误差比定数截尾试验下所得估计值的误差更小,说明双定数混合截尾试验可以提高估计精度. (2)当刻度参数α已知,形状参数的先验分布取Gamma分布时,在平方损失和熵损失函数下, Burr XII分布的失效率H(x)和可靠度R(x)的Bayes估计都比取Jeffreys先验分布更接近真实值. 在双定数混合截尾试验下,对Burr XII分布的失效率和可靠度做估计,在Jeffreys先验分布和Gamma分布下,对不同损失函数下失效率和可靠度的Bayes估计进行比较.结果表明,与定数截尾试验相比,双定数混合截尾试验可以提高失效率和可靠度的估计精度.当形状参数θ的先验分布取Gamma分布时,失效率和可靠度的Bayes估计值比取Jeffreys为先验分布时估计结果更好.1 取共轭先验分布族时的Bayes估计
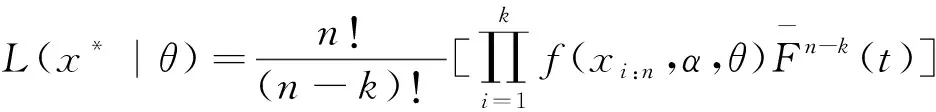
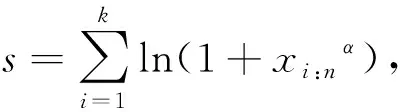

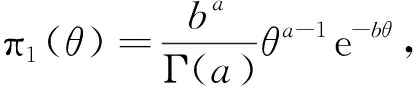
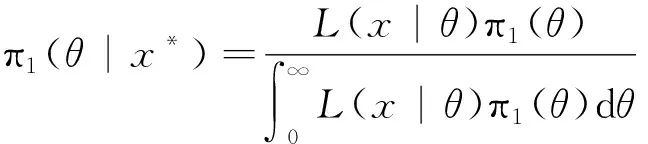
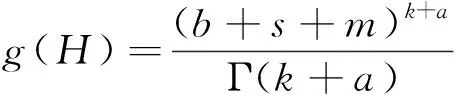
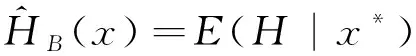
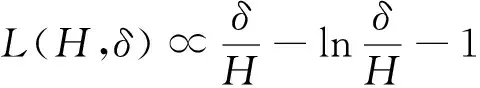
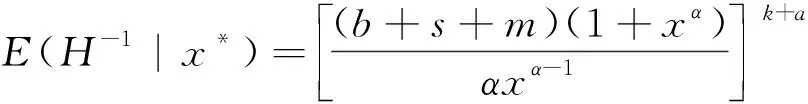
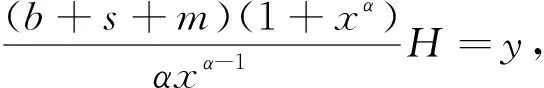
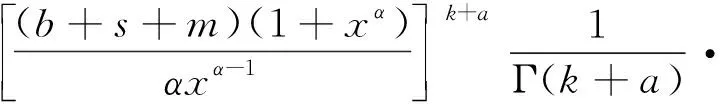


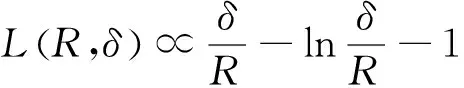
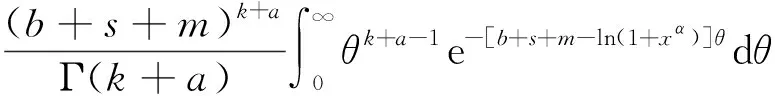
2 取无信息先验时的Bayes估计
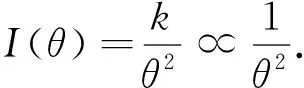

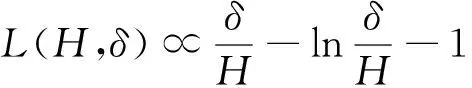
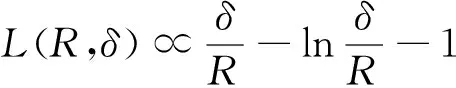
3 算例分析
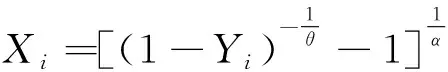

4 结论

