趋化NS系统的全局吸引子
尹艳琼, 范小明
( 西南交通大学 数学学院, 四川 成都 610065)
0 引言
趋化现象刻画的是生物在环境中某些化学物质的影响下产生的一种定向运动.关于它的研究可追溯到Patlak[1]和Keller等[2-3]的创造性工作,他们提出的趋化模型主要研究在化学物质的影响下细菌的聚集过程.而生物学中的许多问题都可以用趋化NS系统来进行模拟[4-10],因此对于数学家和生物学家来说,趋化NS系统已经成为重点的研究数学模型之一[11-13].至今对于此类方程的解的适定性问题已有了大量研究[14-20],但是有关其吸引子的研究甚少.因此本文主要考虑在二维有界域下的趋化NS系统的全局吸引子:
∂tn+u·∇n-Δn=
-∇·(S(n)∇S1(c))-∇·(n∇m)+
f(n,c,m),x∈Ω,t>0,
(1)
∂tc+u·∇c-Δc=-nc-c+k,x∈Ω,t>0,
(2)
∂tm+u·∇m-Δm=
-m+g(c,m),x∈Ω,t>0,
(3)
∂tu+(u·∇)u-Δu=∇p+n∇φ,x∈Ω,t>0,
(4)
∇·u=0,x∈Ω,t>0,
(5)
其中未知函数u=(u1,u2),n,c,m,p分别代表流体速度,细胞种群密度,氧气,化学引诱剂,流体压力.k是一个常数.Ω⊂2是一个带有光滑边界Γ:=∂Ω的有界区域.
针对以上方程,我们考虑n,c,m满足Neumann边界条件,u满足no-slip边界条件
(6)
其中ν(x)是x∈Γ上的单位外法向量.
初始条件
n(x,0)=n0(x),c(x,0)=c0(x),
m(x,0)=m0(x),u(x,0)=u0(x),x∈Ω,
(7)
同时假设φ是重力势并且满足∇φ∈L∞(Ω),Δφ=0.
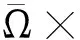
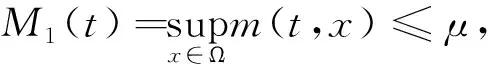
并满足下列条件:
1)0≤f(n,c,m)≤-αn+βc+ηm,其中α是正的常数,β,η是常数.
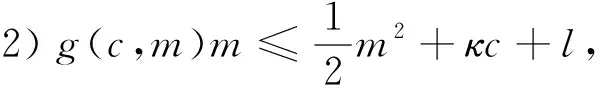

其中γ≤1-2μ-μ1.
本文结构如下:第一部分给出所需的函数空间以及一些基本定义定理;第二部分证明系统吸引子的存在性;第三部分证明系统是一致渐近紧的.
1 预备知识
本章节将会给出一些符号和概念.
L2(Ω)是Hilbert空间,其内积和范数分别为
我们记
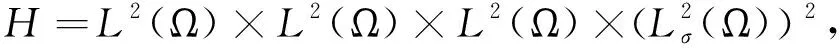
其中
定义1[21-22]设{S(t)}t≥0是算子半群,若紧集A⊂H满足条件:
(1)A是不变集,即S(t)A=A,∀t≥0.
(2)A是一致吸引的,即对于H中的任意一个有界集B,满足
则称A是半群{S(t)}t≥0的全局吸引子.
引理1[22]Ω是n上的有界开集,若对任意的
则有
‖u‖Lq(Ω)≤C‖∇u‖Lp(Ω),

引理2[21]Ω是n上的有界开集,则对任意的
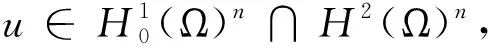
有
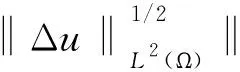
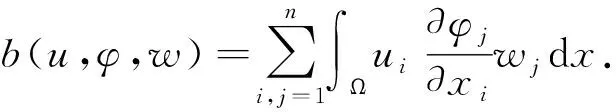
引理3[21](一致 Gronwall 引理) 设y,y1,y2,y′2在[t0,+∞)上均是正的局部可积函数, 若对于t≥t0,满足
y′2≤yy2+y1,


其中r,a1,a2,a3是正的常数.则对∀t≥t0,有
定理1假设S,S′,f,g,h满足以上所给条件,初边值条件满足(6)-(7),则在二维空间上,趋化NS系统 (1)-(5)存在唯一的整体解(n,c,m,u),且∀T>0,有
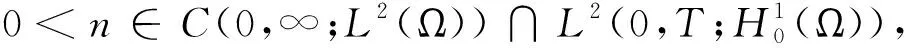
此定理的证明主要是运用Faedo-Galerkin方法[21],可参考文献[23-26],在此不做过多赘述.
根据定理1,可在空间H上定义连续的算子半群{S(t)}t≥0:
下面运用Temam[21]的研究方法推出在空间H上半群{S(t)}t≥0的全局吸引子A存在.
2 吸收集
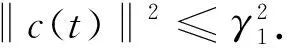
证方程(2)的两边分别与c作L2(Ω)的内积

故有
(8)
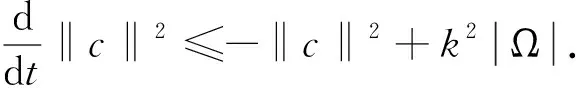

设B1是L2(Ω)中的一个有界集,包含在以RB1为半径、0为圆心的球领域里面.则存在常数γ1>ρ1,以及
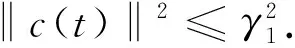
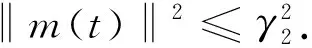
证由引理4可知,c从L2(Ω)的任一有界集出发,时间t1过后,总是会回到吸收集B1中,其中B1是ο(0,γ1)在L2(Ω)中的有界闭集,故可设c总在B1中.方程(3)的两边分别与m作L2(Ω)的内积
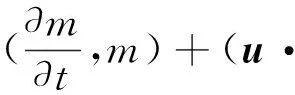
(-m,m)+(g(c,m),m).
由条件2)可得
(g(c,m),m)≤
再由引理4可得
即

(9)
故
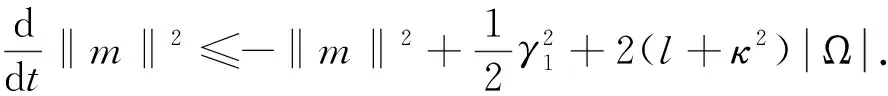
由Gronwall不等式,有
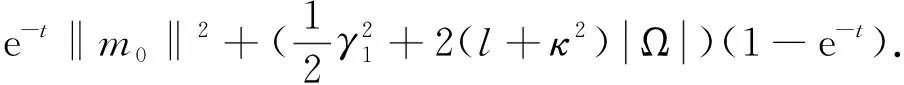
设B2×B1是L2(Ω)×L2(Ω)中的一个有界集,包含在以RB2×B1为半径、0为圆心的球领域里面.则存在常数
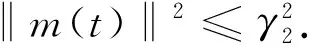
由引理5可知,(m,c)从L2(Ω)×L2(Ω)的任一有界集出发,时间t2过后,总是会回到吸收集B2×B1中,其中Bi(i=1,2)是ο(0,γi)(i=1,2)在L2(Ω)中的有界闭集,故可设(m,c)总在中B2×B1.
引理6从吸收集B2×B1出发的解(c,m)满足


证方程(3)的两边分别与m作L2(Ω)的内积
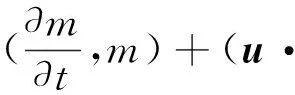
(-m,m)+(h(n,m),m).

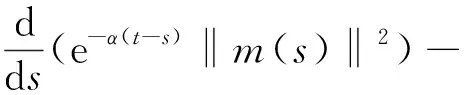
由引理4可得
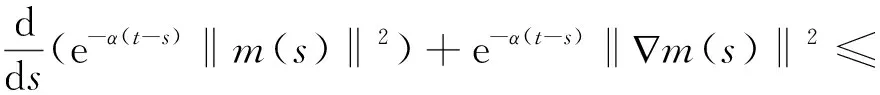
从0到t对s进行积分,有

则

对方程(2)的两边分别与c作L2(Ω)的内积

(-nc,c)+(-c+k,c).

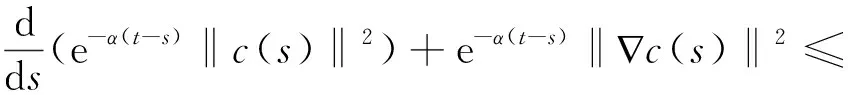
由引理5可得
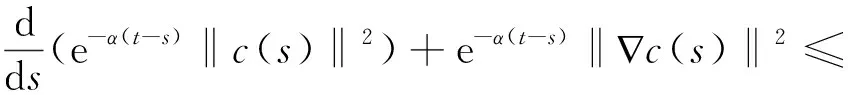
从0到t对s进行积分,有
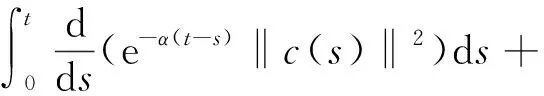
则

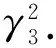
证对方程(1)的两边分别与n作L2(Ω)的内积,得到

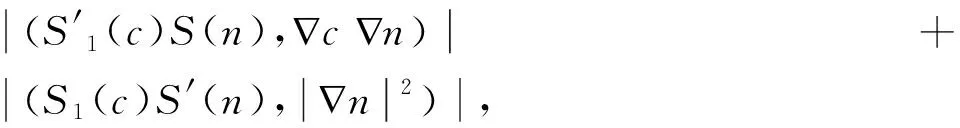
再由条件3)可得
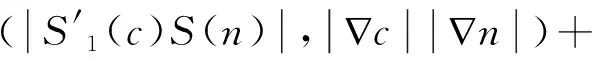
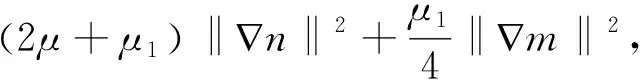
再由条件1)、引理4、引理5及Young不等式,可得
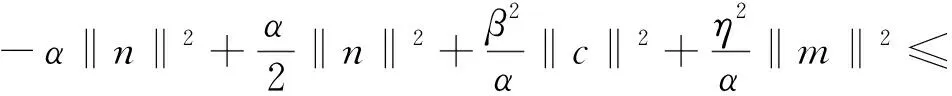
故
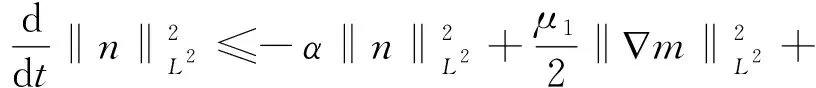
(10)
令
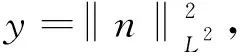
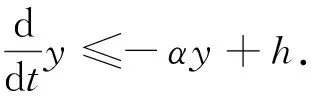
由引理6可得

其中
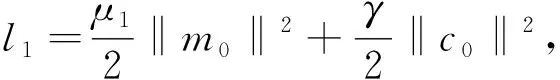
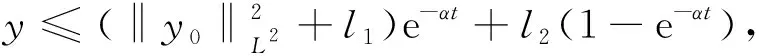
设B3×B2×B1是L2(Ω)×L2(Ω)×L2(Ω)中的一个有界集,包含在以RB3×B2×B1为半径,0为圆心的球领域里面.则存在常数γ3>ρ3,
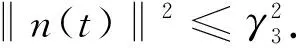
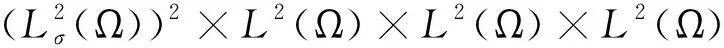
证由引理7可知,(n,c,m)从L2(Ω)×L2(Ω)×L2(Ω)中的任一有界集出发,时间t3过后,总会回到吸收集B3×B2×B1中,其中Bi(i=1,2,3)是ο(0,γi)(i=1,2,3)在L2(Ω)中的有界闭集,故可设(n,c,m)总在B3×B2×B1中.


(∇p,u)+(n∇φ,u).
此时压力项将会消失,得到

因为∇φ∈L∞(Ω),故存在一个常数C,使得‖∇φ‖L∞ (11) 利用Gronwall不等式,得 定理2由方程(1)-(5)生成的解半群{S(t)}t≥0,在H上具有一个正向有界不变的吸收集. 引理9设(u,n,c,m)∈,其中 为有界吸收集,则对任意固定r>0,存在常数γ5(r)>0,γ6(r)>0,γ7(r)>0,γ8(r)>0,使得 证因为(u,n,c,m)∈,故式(8)-(11)成立.对任意固定r>0,将式(11)两边同时从t到t+r对s进行积分,有 由引理8可知,存在常数 使得 将式(9)两边同时从t到t+r对s进行积分,有 由引理5可知,存在常数 将式(8)两边同时从t到t+r对s进行积分,有 将式(10)两边同时从t到t+r对s进行积分,有 由引理7可知,存在常数 本节证明半群{S(t)}t≥0是一致渐近紧的,设B⊂H是{S(t)}t≥0正向不变集, (n,c,m,u)是系统(1)-(5)的解.现只需证明从B出发,最终此系统的解进入K的有界集. 证将方程(4)两边同时乘以-Δu,并在Ω上积分,得 (∂tu,-Δu)-(Δu,-Δu)= ((u·∇)u,Δu)+(n∇φ,-Δu). 由Young不等式和引理8,有 使用一致Gronwall引理可得 证将方程(2)两边同时乘以-Δc,并在Ω上积分,得 (∂tc,-Δc)-(Δc,-Δc)= 其中k2是充分大的正常数. 故有 (12) 对上式关于s从0到r积分,可得 由定理8可得 证将方程(2)两边同时乘以-Δc,并在Ω上积分,得 (∂tm,-Δm)-(Δm,-Δm)= 其中k3是充分大的正常数. 从而 故,由引理11,有 (13) 对上式关于s从0到r积分,可得 证方程(4)两边同时乘-Δn,并在Ω上积分 (∂tn,-Δn)-(Δn,-Δn)= 其中k5为充分大的正常数. 从而 其中 则 任意的T>0,对式(12)、(13)分别在区间[0,T]上积分,可得 再由引理11和引理12,可得 定理3由方程(1)-(5)生成的解半群{S(t)}t≥0是一致渐近紧的. 由定理2和定理3可得以下定理. 定理4由方程(1)-(5)生成的解半群{S(t)}t≥0,在H上具有一个全局吸引子. 本文利用Temam等人的理论,证明了在二维空间下趋化NS系统存在全局吸引子.一般地,在获得系统的吸收集和算子{S(t)}t≥0的一致渐近紧性时,我们将几个方程抽象为一个整体进行处理.而本文在证明过程中将方程分为四个部分,分别在对应的函数空间上进行证明,并且证明的顺序是不可改变的.在以后的研究中,可进一步讨论此类方程的吸引子维数,以及在三维空间下研究其吸引子的存在性问题和吸引子维数问题.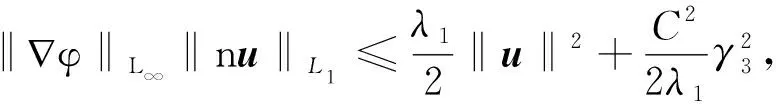

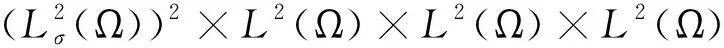
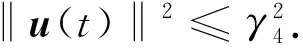
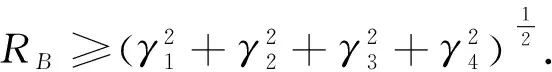

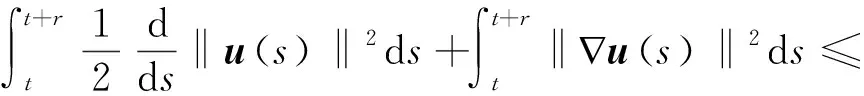



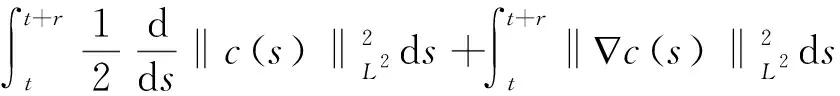
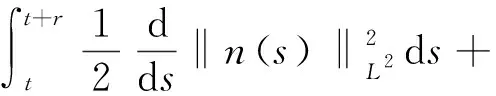

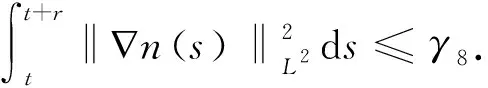
3 渐近紧性
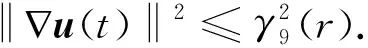

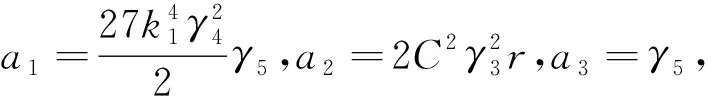

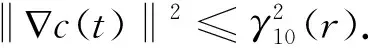
(u·∇c,Δc)+(nc,Δc)+(-c+k,-Δc).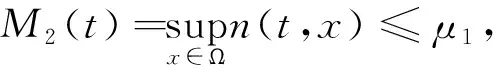

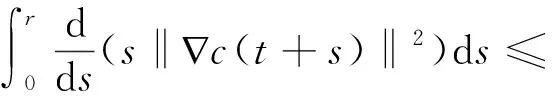
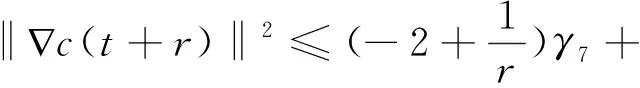

(u·∇m,Δm)-(m,-Δm)+(g(c,m),-Δm).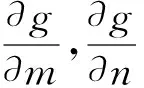
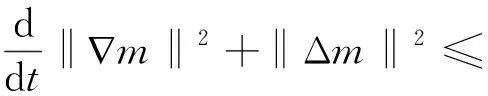
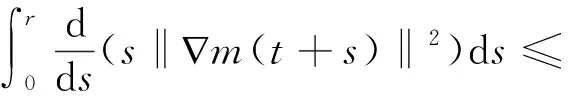
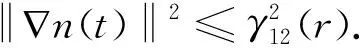
(u·∇n,Δn)+(-∇·(S(n)∇S1(c)),-Δn)-
(∇·(n∇m),-Δn)+(f(n,c,m),-Δn),
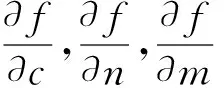
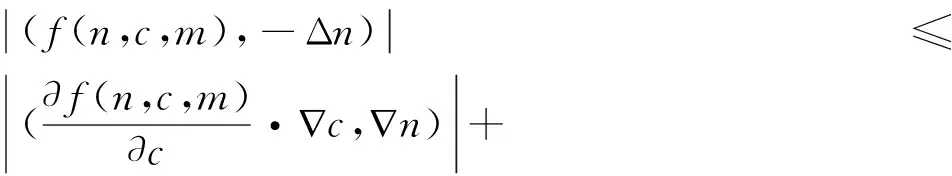
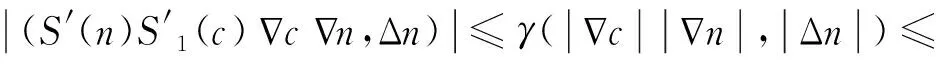
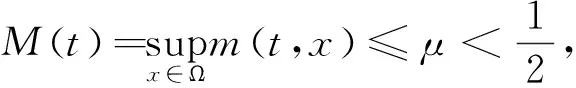
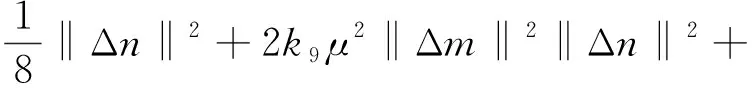
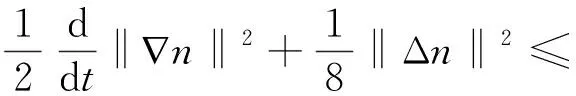

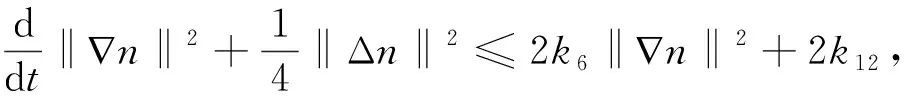
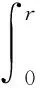

4 结论

