浅谈初中数学教学中的变式教学

许晓枫

摘要：变式教学是连接双基与创新的纽带。在初中数学教学中常用变式题进行教学，变式题是把原问题加以变化形成新问题，通过例题、习题变式，使学生在变化中发现其规律和本质，可拓展学生的思维。促使学生自觉将数学学习技术内化为主体需要，使教学过程成为有利于学生积极探究的过程，提高学生的学习效能。在初中数学教学过程中，应用变式题有什么技巧，本文就该问题进行浅要分析。

关键词：初中数学 教学 变式题 有效教学

前言

《数学新课程标准》指出：学生的数学学习内容应当是现实的、有意义的、富有挑战性的，这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动。数学教学过程不仅是课本知识的传授，更重要的是对学生能力的训练和情操的培养，尤其要重视学习能力和学习方法的培养。数学教学的本质就是利用数学规律进行变式教学解决实际问题的过程，教师适当地对数学题进行演变、引申和拓展，不仅可以有效提高学生对数学的探索、应变能力，还能激发其发散性、广阔性思维，使学生观察思考问题更加多角度，提高学生思维的严密性、整体性，最终达到提高学生综合素质的目的。抓住典型习题，寻求多种解题途径，促使学生的思维向多层次、多方向发散。注重这种变式模式的教学，对提高学生分析问题和解决问题的能力大有益處。

因此，在例题、习题教学中，当学生获得某种基本解法后，教师应引导学生发掘例、习题的潜在因素，通过改变题目的条件、探求题目的结论、改变情境等多种变式途径，强化学生对知识和方法的理解，帮助他们对问题进行多角度、多层次的思考。同时变式题教学要把握好度，在进行变式题练习时，数学教师要引导学生主动参与意识，鼓励学生自主大胆的变式，活跃课堂氛围，激发学生积极学习的兴趣。

一、在形成数学概念的过程中，利用变式启发学生积极参与观察、分析、归纳，培养学生正确概括的思维能力

从培养学生思维能力的要求来看，形成数学概念，提示其内涵与外延，比数学概念的定义本身更重要。在形成概念的过程中，可以利用变式引导学生积极参与形成概念的全过程，让学生自己去“发现”去“创造”，通过多样化的变式提高学生学习的积极性，培养学生的观察、分析以及概括能力。

如在讲分式的意义时，一个分式的值为零是指分式的分子为零而分母不为零，因此对于分式[x+12x-3]的值为零时，在得到答案[x=-1]时，实际上学生对“分子为零而分母不为零”这个条件还不是很清晰，难以辨析出学生是否考虑了“分母不为零”这个条件，此时可以做如下变形：

变形1：当x__________时，分式[x2-1/2x-3]的值为零？（分子为零时x=[±1]）

变形2：当x__________时，分式[x2-1/x-1]的值为零？（[x=1]时分母为零因此要舍去）

通过以上的变形，可以对概念的理解逐渐加深，对概念中本质的东西有个非常清晰的认识，因此教师在以后的练习中也明确类似知识点的考查方向，防止教师盲目出题，学生盲目练习，在有限的时间内使得效益最大化。

二、在解题教学中，利用变式来改变题目的条件或结论，揭示条件、目标间的联系，解题思路中的方法之间的联系与规律，从而培养学生联想、转化、推理、归纳、探索的思维能力

（一）多题一解，适当变式，培养学生求同存异的思维能力

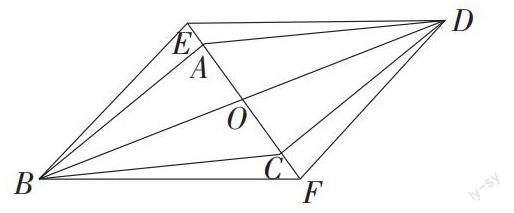
例题：已知，如图6-13（1），在平行四边形ABCD中，点E、F在对角线AC上，并且AE=CF.求证：四边形BFDE是平行四边形吗？

证明： 如图，连接BD交AC于点O.

∵ 四边形ABCD是平行四边形

∴ OA=OC OB=OD

又∵AE=CF

∴OA-AE=OC-CF

∴OE=OF

∴四边形BFDE是平行四边形

【变式练习】

变式1：对于上述例题，若E，F继

续移动至OA，OC的延长线上，仍使AE=CF（如图），则结论还成立吗？若成立，请证明。

变式2：已知：E、F是平行四边形ABCD对角线AC的两点，若BE//DF，四边形BFDE是平行四边形吗？

变式3：如图所示，四边形ABCD的对角线相交于点O，若AB∥CD，请添加一个条件             （写一个即可），使四边形ABCD是平行四边形。

（二）一题多问，通过变式引申发展，扩充、发展原有功能，培养学生的创新意识和探究、概括能力

例题：某工厂去年的利润（总产值—总支出）为200万元。今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元。去年的总产值、总支出各是多少万元？

分析：设去年的总产值为x万元，总支出为y元

变式问题：若条件不变，求今年的总收入、总支出是多少万呢？

变式：某工厂去年的利润（总产值—总支出）为200万元。今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元。今年的总产值、总支出各是多少万元？

由这道题可知：设间接未知数，设去年的总收入为x万元，总支出为y万元，计算更方便些。

这一组变式教学经历了一个特殊到一般的过程，有助于深化、巩固知识，培养学生的问题意识和探究意识。

（三）一题多变，总结规律，培养学生思维的探索性和深刻性

通过变式教学，不是解决一个问题，而是解决一类问题，开拓学生解题思路，培养学生的探索意识，实现“以少胜多”。

例题：如左图，有一块三角形余料ABC，它的边BC=120mm，高AD=80mm。

要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点

分别在AB、AC上。问加工成的正方形零件的边长为多少mm？

变式1：将“正方形PQMN”改为“矩形PQMN”。问矩形的长和宽分别为多少时，所截得的矩形面积最大？最大面积是多少？余料的利用率是多少？

变式2：一块直角三角形木板的一条直角边AB长为1.5[m]，面积为1.5[m2]，工人师傅要把它加工成一个面积最大的正方形桌面，请甲乙两位同学设计加工方案，甲设计方案如图（1）所示，乙设计方案如图（2）所示。你认为哪位同学设计的方案较好？试说明理由。（加工损耗忽略不计，计算结果可保留分数）

（四）多题一解，异中求同

由问题的条件或结论的外形结构，联想到与其形式类似的有关题型，从而获得转化桥梁，打开解题思路。

【案例】如图1，一块铁皮呈锐角三角形，它的边BC=80cm，高AD=60cm，要把它加工成矩形零件，使矩形的长、宽之比为2：1，并且矩形长的一边位于BC上，另两个顶点分别在边AB、AC上。求这个矩形零件的长与宽。

变式1：如图1，一块铁皮呈锐角三角形，它的边BC=80cm，高AD=60cm，要把它加工成矩形零件，使矩形的长、宽之比为2∶1，并且矩形长的一边位于BC上，另两个顶点分别在边AB、AC上。（1）求这个矩形的周长；（2）求这个矩形的面积；（3）求△APQ的面积。

变式2：如图2，一块铁皮呈三角形，∠BAC=90°，要把它加工成矩形零件，使矩形一边位于BC上，另两个顶点分别在边AB、AC上。试问：PS、BS、CR之间有何关系？为什么？

变式3：如图2，一块铁皮呈锐角三角形，它的边BC=80cm，高AD=60cm，要把它加工成矩形零件，矩形的一边位于BC上，另两个顶点分别在边AB、AC上。求这个矩形面积的最大值。

总之，在教学中，我们既要有强烈的变式意识，娴熟的变式方法，更要遵循变式教学的规律，合理安排变式教学的内容。如果我们能够遵循学生认知发展规律，根据教学内容和目标加强变式训练，对巩固基础、培养思维、提高能力有着重要的作用。变式训练能培养培养学生敢于思考，敢于联想，敢于怀疑的品质，培养學生自主探究能力与创新精神。当然，课堂教学中的变式题最好以教材为源，以学生为本，体现出“源于课本，高于课本”，并能在日常教学中渗透到学生的学习中去。让学生也学会“变题”，使学生自己去探索、分析、综合，以提高学生的数学素质。培养学生创造性思维，激发学生学习数学的兴趣，提升学生的数学核心素养。