如何用图象法解答三角函数问题
王继祖

图象法是解答三角函数问题的重要方法.运用图象法解题,需根据三角函数的解析式画出相应的图象,通过数形结合来求得问题的答案.图象法常用于研究三角函数的性质、解三角不等式、解答三角函数零点问题.下面结合实例探讨一下,用图象法解答这三类三角函数问题的思路.
一、利用图象法研究三角函数的性质
三角函数的图象可以直观地反映出三角函数的所有性质.在解答有关三角函数性质问题时,我们可以先画出三角函数的图象,通过研究和分析三角函数的图象,了解函数图象的变化趋势,进而确定函数的最小值、单调性、对称性、奇偶性、周期性、与坐标轴的交点等.
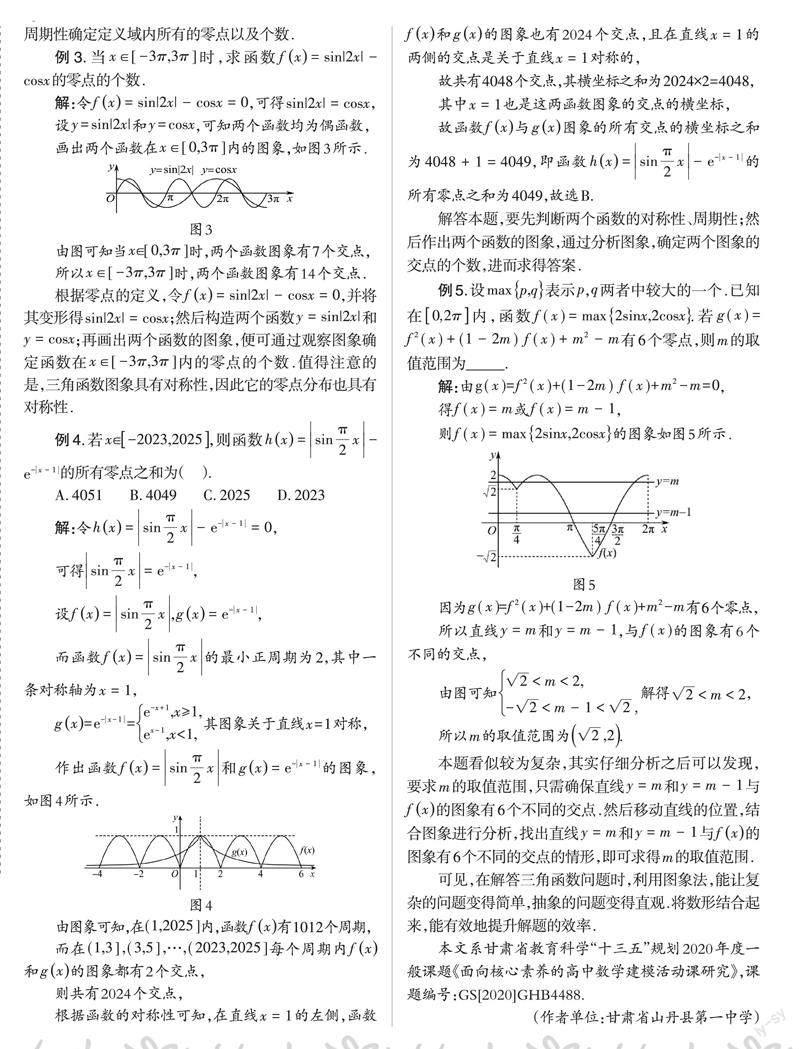
由图1可知[fx]的周期为[9π4-π4=2π],则A项错误;
[fx]的减区间为[π4+2kπ,π+2kπk∈Z]和 [5π4+2kπ,3π2+2kπk∈Z],则B项错误;
[fx]的最大值为[fπ4=22],则C项错误;
[fx]图象的对称轴为[x=π4+kπk∈Z],D项正确.故选D.
该三角函数式中含有绝对值,需去掉绝对值符号,用分段函数表示.再根据函数的解析式画出图象,通过观察图象,即可明确三角函数的周期、单调区间、最值、对称轴,从而快速判断出四个选项的对错.利用函数的图象去研究三角函数的性质,既清楚明了,又便捷.
二、利用图象法解三角不等式
解三角不等式,通常要用到三角函数的图象和性质.在解题时,可根据不等式的结构特征,构造出一个或两个三角函数模型,将问题转化一个三角函数图象上两点之间的位置关系问题,或两个三角函数图象之间的位置关系问题.通过研究函数的图象,便可找出使不等式成立的位置关系,进而求得不等式的解集.利用图象法解三角不等式,关键是确定函数图象的交点,或函数图象与x轴的交点,并根据图象找出满足不等式的部分曲线.
要使当x∈(0,2π)时,sinx>|cosx|,需使y=sinx的图象始终在y=|cosx|的下方,此时x∈[π4,3π4].故选A.
我们将三角不等式左右两边的式子分别构造成函数,即y=sinx与y=|cosx|;然后根据函数的解析式画出当x∈(0,π)时两个函数的图象.通过观察可发现,两个函数存在交點,于是求得两个函数图象的交点,并找出y=sinx的图象在y=|cosx|的图象下方的一段曲线,求出对应的x的取值范围,即可求得不等式的解集.
三、利用图象法解答三角函数零点问题
函数的零点是函数为0时x的取值,即函数图象与x轴的交点的横坐标.而三角函数的零点往往不会只有一个,因而在解题时,要先画出三角函数的图象,并找出一个周期内函数图象与x轴的交点;然后根据三角函数的周期性确定定义域内所有的零点以及个数.
根据零点的定义,令[fx=sin|2x|-cosx=0],并将其变形得[sin|2x|=cosx];然后构造两个函数[y=sin|2x|]和[y=cosx];再画出两个函数的图象,便可通过观察图象确定函数在[x∈[-3π,3π]]内的零点的个数.值得注意的是,三角函数图象具有对称性,因此它的零点分布也具有对称性.
故函数[fx]与[gx]图象的所有交点的横坐标之和为[4048+1=4049],即函数[hx=sinπ2x-e-x-1]的所有零点之和为4049,故选B.
解答本题,要先判断两个函数的对称性、周期性;然后作出两个函数的图象,通过分析图象,确定两个图象的交点的个数,进而求得答案.
例5.设[maxp,q]表示[p],[q]两者中较大的一个.已知在[0,2π]内,函数[f(x)=max2sinx,2cosx].若[g(x)=f2(x)+(1-2m)f(x)+m2-m]有[6]个零点,则[m]的取值范围为_____.
本题看似较为复杂,其实仔细分析之后可以发现,要求m的取值范围,只需确保直线[y=m]和[y=m-1]与[fx]的图象有6个不同的交点.然后移动直线的位置,结合图象进行分析,找出直线[y=m]和[y=m-1]与[fx]的图象有6个不同的交点的情形,即可求得m的取值范围.
可见,在解答三角函数问题时,利用图象法,能让复杂的问题变得简单,抽象的问题变得直观.将数形结合起来,能有效地提升解题的效率.
本文系甘肃省教育科学“十三五”规划2020年度一般课题《面向核心素养的高中数学建模活动课研究》,课题编号:GS[2020]GHB4488.

