彰显模型思想 凸显推理能力 尽显素养立意
——一道“含参二次函数”中考题的解法赏析与教学启示
江苏省南京市竹山中学 夏乾冬 (邮编:211100)
江苏省无锡市太湖格致中学 陈 锋 (邮编:214125)
2023年中考数学江苏南京卷第25题,与其他省市中考试题中二次函数与几何图形的糅合考查不同,它是基于含参二次函数,利用参数对二次函数图像以及性质的影响,考查整式的运算、二次函数、方程、不等式等“数与代数”领域的核心知识.试题设置3小问,文字表述简约、严谨,入口宽,思维拾级而上,既能体现对基本知识、基本技能以及基本思想方法的考查,又能体现对思维品质和综合能力的考查,彰显模型思想、凸显推理能力、尽显素养立意.
1 试题呈现
(南京中考第25题)已知二次函数y=ax2-2ax+3(a为常数,a≠0)
(1)若a<0,求证:该函数图像与x轴有两个公共点;
(2)若a=-1,求证:当-1
(3)若该函数的图像与x轴有两个公共点(x1,0),(x2,0),且-1 《义务教育数学课程标准(2022年版)》(以下简称《课标(2022年版)》)在“函数教学”中指出“理解函数图像与表达式的对应关系,理解函数与对应的方程、不等式的关系”[1].方程、不等式和函数是刻画现实世界的有效模型,本试题的命制与课标要求吻合.例如,本题中第(1)问是二次函数图像与x轴的交点问题,可以从函数角度分析,也可以从方程的角度分析.第(2)问求证-x2+2x+3>0,可以从不等式的角度分析,也可函数的角度分析.因此,本题通过建立模型,选择模型,从不同的数学模型来分析问题,彰显模型思想. 《课标(2022年版)》中指出:“在义务教育阶段,数学思维主要表现为运算能力、推理意识或推理能力”.代数推理作为一种手段,其目标可以是求得(发现)未知结果或结论,也可以是证明(确定)已知结果或结论[2].试题的3小问也都可以利用代数推理解决,然而解决问题的思维水平逐级提升.第(1)问中,判断一元二次方程ax2-2ax+3=0(a<0)有两个不相等的实数根即可,这里可以证b2-4ac>0,也可以解方程,并说明两根不相等,学生有一定的知识和技能储备.然而第(2)问需要将问题转化成:当-1 本题中的参数a,一参二用,a用作二次项系数,-2a用作一次项系数,而不是使用多个参数去为难学生.其中,a既能决定开口方向,又能刻画开口的大小以及顶点的位置,但不决定对称轴,感受“变中有变”和“变中不变”.第(1)、(2)问要求学生写出过程,考查学生用数学语言或图形语言进行说理,做到“步步有据,句句有理”的规范表达,突出数学的严谨性.第(3)问以填空题的形式出现,而没有刻意提示学生“结合函数图像”,学生可以从几何直观、代数推理等多个的角度进行思考,然而不同角度带来的思维难度、运算能力的要求都不一样,有助于对学生思维能力的甄别. 本题蕴含着从特殊到一般、数形结合、分类讨论以及转化等思想方法的渗透,算式的建立、求解与证明,考查学生的几何直观、数学建模、数学运算和推理能力等素养,实现了对数学核心素养的综合考查. 思路1建立一元二次方程模型求证 法1因为令y=0,即ax2-2ax+3=0,所以b2-4ac=4a2-12a=4a(a-3),因为a<0,所以4a<0,a-3<0,所以b2-4ac=4a(a-3)>0.所以方程有两个不相等的实数根,所以该函数图像与x轴有两个公共点. 思路2利用二次函数模型求证 法3因为y=ax2-2ax+3=a(x-1)2+3-a,所以该函数图像的顶点为(1,3-a).因为a<0,所以该函数图像的开口向下,且-a>0,所以3-a>0.即该函数图像的顶点在x轴上方.所以由图像可知,该函数图像与x轴有两个公共点. 法4因为a<0,所以二次函数图像开口向下.因为x=0时,y=3,所以与y轴的交点为(0,3).因为二次函数图像与y轴的交点为(0,3)且开口向下,所以当a<0时,该函数图像与x轴有两个公共点. 思路1利用二次函数模型求证 法1当a=-1时,y=-x2+2x+3=-(x-1)2+4,所以该函数图像对称轴为直线x=1.所以当-1 法2因为当a=-1时,y=-x2+2x+3,所以可画图像如图1所示;所以由图像可知,当-1 图1 思路2利用不等式模型求证 法3因为当a=-1时,y=-x2+2x+3=-(x-1)2+4,又因为-1 所以-2 法4当a=-1时,y=-x2+2x+3=(-x+3)(x+1).而-1 法5当a=-1时,y=-x2+2x+3.因为-1 法6因为当a=-1时,所以y=-x2+2x+3.因为当y>0时,所以-x2+2x+3>0,即(-x+3)(x+1)>0. 解得:-1 思路1利用函数和不等式模型求解 法1画出满足条件的图形,建立不等式组 因为y=ax2-2ax+3=a(x-1)2+3-a,所以该函数图像对称轴为直线x=1,顶点为(1,3-a).因为当x=0时,y=3;所以二次函数图像经过定点(0,3). ①当a<0时,画出y=ax2-2ax+3的草图,如图2.因为-1 图2 解得a<-1. ②当a>0时,画出y=ax2-2ax+3的草图,如图3.因为当顶点在x轴下方时,满足-1 图3 思路2利用函数和方程模型求解 法2画出临界情况,建立方程 ①当a<0时,画出y=ax2-2ax+3的草图, 如图4.寻找临界情况(虚线),此时,图像经过点(-1,0).当x=-1时,y=0,即a+2a+3=0,解得a=-1.在临界情况的基础上,当图像的开口变小时,满足-1 图4 ②当a>0时,画出y=ax2-2ax+3的草图,如图5.寻找临界情况(虚线),此时,图像与x轴只有一个公共点(顶点在x轴上),即3-a=0,解得a=3.在临界情况的基础上,当图像的开口变小时,满足-1 图5 思路3利用不等式模型求解 法3当y=0时,ax2-2ax+3=0, 模型思想可以在数学解题过程中提供一种思维突破口,教师不仅需要引导学生积极敏锐地去发现题目条件与所求问题之间的丝缕关联,还要鼓励学生在已知的数学信息中探讨模型的分类,并对不同解法进行探究、归纳总结,最终形成对应的解题方法.例如,本题的第(3)问,如果学生对二次函数图像和性质掌握透彻,能够从“形”入手,再结合方程和不等式来分析,那么这个问题的解决方法就很容易能想到,解法显得简便、简洁.此时,需要根据含参函数中寻找“确定”条件,即图像经过两个定点(0,3)、(2,3)和对称轴直线x=1,虽然,顶点(1,3-a)不完全确定,但也很重要.此时,还要根据二次项系数a的正负进行分类讨论,分别画出开口向上、向下两种情形,画出符合条件的草图.接下来,需要结合图像寻找特殊的“点”(顶点、与x轴的交点等)满足要求的不等式,建立不等式组求解,或者寻找临界情况后,建立方程求解.利用“a决定形状、开口大小,a的绝对值越大(小),开口就越小(大)”确定a的取值范围.当然,也可以只从不等式的角度分析.这也是实现“数”“形”转化的关键所在,是教师培养学生数学抽象能力的重要发力点.因此,教师在解题教学中要引导学生分析其中的确定元素,从“形”的特点出发,借助图形分析和解决问题. 在此情况下,如何寻找有效的解题模型?需要运用模型思想进行分析,碰到障碍适时调整建立模型的方法,并灵活调整解题模型,最终解决问题.因此,在平时教学中,教师要在问题求解的过程中,有意识地渗透模型思想,经历建立方程、函数等数学模型求解问题的过程,不断提升学生的解题能力. 在实际的教学过程中,教师往往忽视代数推理,认为几何证明才是发展学生推理能力的重要方面.事实上,推理是逻辑推理的重要组成部分,在培养学生推理能力方面有着不可替代的作用.本题的诸多解法中,大量使用到推理,说明推理在问题求解中有着非常重要的作用.例如,第(1)、(2)问的代数推理证明中,要引导学生知道证明的条件、结论是什么?如何由“果”索“因”或由“因”导“果”?需要用到哪些代数中的运算公式、法则、性质?教师要进行解题示范,规范证明的步骤,明白每一步的依据,即代数推理证明的“基本套路”.最后,还要引导学生进行反思.例如,第(1)、(2)问中为什么这样证可以?为什么那样证不行?推理教给学生的不仅是解决问题的方法,更要培养学生重论据、合逻辑的思维习惯,帮助学生形成实事求是的科学态度和理性精神.因此,在数学教学中,教师应重视代数推理的教学,准确把握推理教学的时机,依托教学内容,适时、适度、适切地渗透推理的知识,培养学生逻辑推理的能力. 在“数与代数”领域,是学生形成抽象能力、模型思想、几何直观、运算能力、推理能力、感悟用数学语言表达世界的重要载体.教学中,教师要让学生经历知识的发现或问题解决的全过程,加强学法指导,培养数学能力,发展数学素养.2 试题评价
2.1 立足核心知识,彰显模型思想
2.2 关注数学思维,凸显推理能力
2.3 聚焦关键能力,尽显素养立意
3 解法赏析
3.1 关于第(1)问
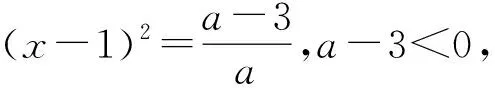
3.2 关于第(2)问
3.3 关于第(3)问
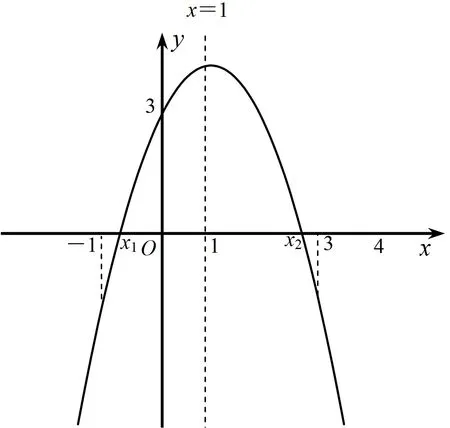
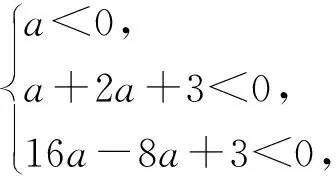
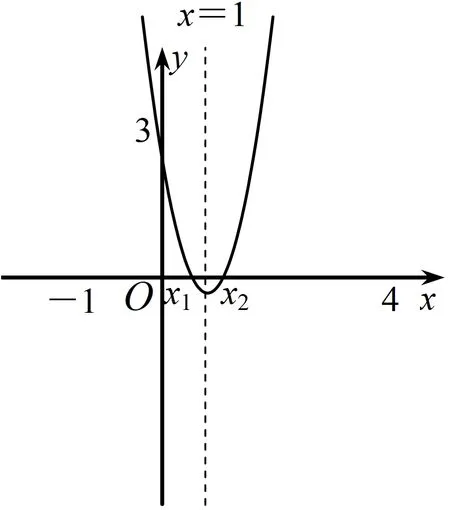

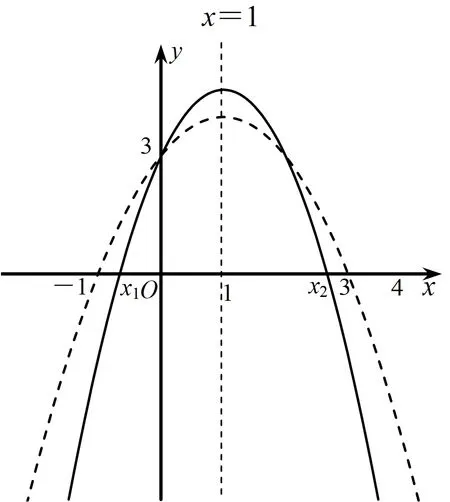
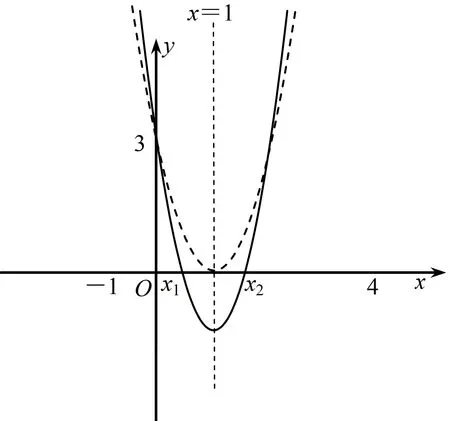
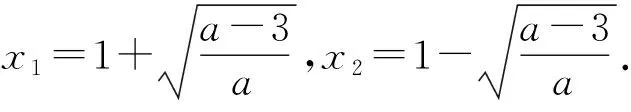
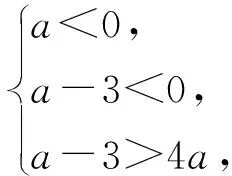
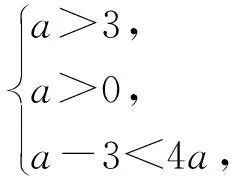
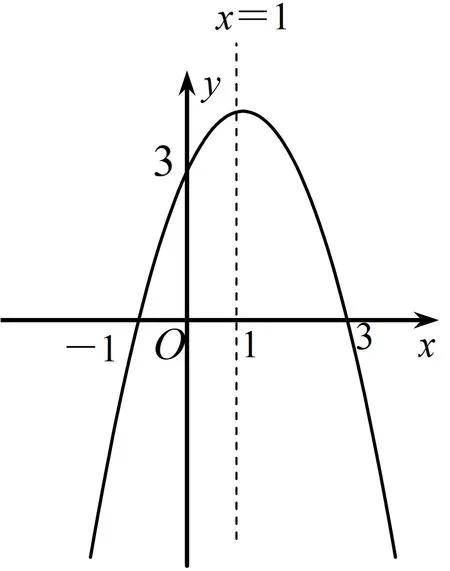
4 教学启示
4.1 强化知识关联,注重模型思想
4.2 加强学法指导,重视推理能力

