基于双层规划模型的高速公路差异化收费定价研究

程思洁 邵晓明 李镇 王江锋

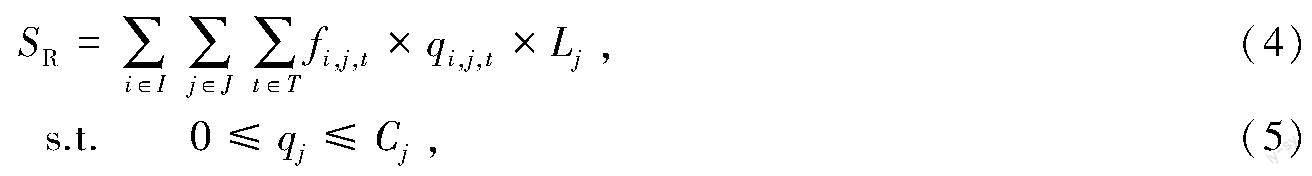
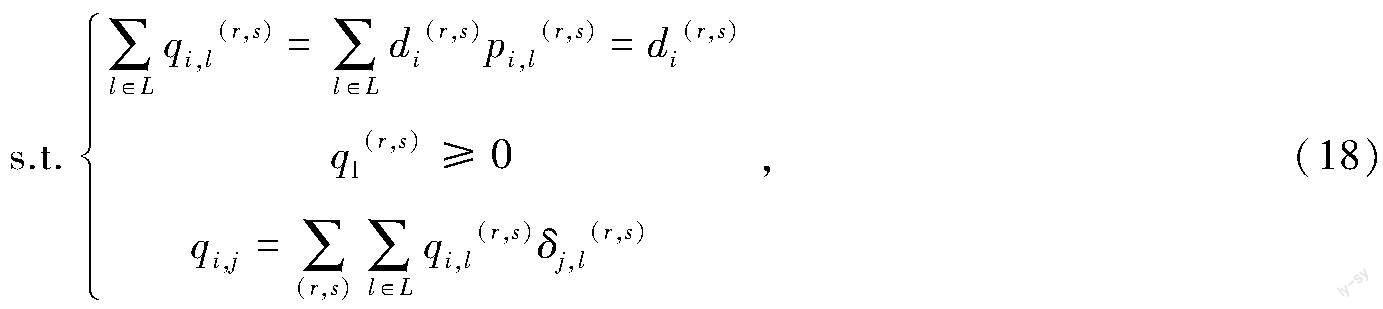
摘要：为了提高高速公路利用率，减轻平行国省道的交通负担，综合考虑高速公路经营者和使用者双方的利益，建立了以实现高速公路运营收益增加为上层目标，以实现路网多用户随机均衡分配为下层目标的差异化收费定价模型，设计了遗传算法和模拟退火算法与迭代加权法组合的模型求解算法。在分析山东省龙青高速及其平行国省道交通流特征的基础上，运用设计的模型有针对性地制定分出入口路段、分时段、分车型的高速公差异化收费方案。研究结果表明最优的差异化收费方案能使龙青高速北向南方向的运营收益增加786.19万元/年，道路使用者的出行成本减少716.51万元/年，验证了差异化收费定价模型的实用性，进一步完善了高速公路多模式差异化收费方案。

关键词：高速公路；差异化收费；双层规划；广义费用函数；多用户随机均衡分配；遗传算法；模拟退火算法；迭代加权法

中图分类号：U491.1+22   文献标志码：A   文章编号：1002-4026（2023）05-0093-09

Research on differentiated toll pricing for highways based on bi-level programming

CHENG Sijie1，SHAO Xiaoming2，LI Zhen3，WANG Jiangfeng1*

（1. Key Laboratory of Transport Industry of Big Data Application Technologies for Comprehensive Transport， School of Traffic and Transportation， Beijing Jiaotong University， Beijing 100044， China；2. Shandong Provincial Communications Planning and Design Institute Group Co.Ltd，Jinan 250101， China；3. Shandong Hi-speed Company Limited，Jinan 250013， China）

Abstract∶To improve the utilization of highway resources and the traffic situation in parallel national and provincial roads， in this study， the interests of highway operators and users was comprehensively accounted; a differentiated toll pricing model with the upper-level objective of increasing highway operating revenues and the lower-level objective of achieving multiclass stochastic traffic network equilibrium was established; and a model incorporating the genetic algorithm， simulated annealing algorithm， and iterative weighting method was developed. Based on the analysis of the traffic characteristics of the Longqing highway and its parallel national and provincial roads in the Shandong Province， the proposed model was used to develop differential toll schemes for entrance and exit sections， time periods， and vehicle types on the highway. The results show that the optimal differentiated tolling schemes can increase the operating revenue of the Longqing highway in the north-south direction by 7861900 yuan/year and reduce the travel cost of the road network by 7 165 100 yuan/year， which confirms the practicality of the proposed model and the effectiveness of the multimode differentiated tolling schemes for highways.

Key words∶highway; differentiated tolling; bi-level programming; generalized cost functions; multiclass stochastic traffic network equilibrium; genetic algorithm; simulated annealing algorithm; iterative weighting method

公路是我國覆盖范围最广、通达程度最深的交通基础设施。近年来公路网交通流分布不均衡的问题日益严重，国省道公路拥堵频发，部分路段交通流量过大，给路面造成了巨大的损耗，增加了公路养护和维修的成本。高速公路凭借良好的道路条件、高效的运输效率，承担起了支撑经济社会发展“大动脉”的作用，但其通行费率依旧在车辆的出行成本中占据较大的比重，高额的出行成本影响了高速公路的竞争力。差异化收费是解决这一问题的有效方式，通过经济杠杆的作用提升道路交通吸引力，对路网的交通流进行有效引导，优化路网交通流分配，从而有效提升路网使用效率，改善路网循环质量、提高交通运输效率、降低运输成本，促进经济和社会的发展。

高速公路收费定价问题的研究涉及政府、道路使用者和运营者等多方利益，需要考虑成本、收益、交通量、污染排放等因素[1-4]。目前主要的高速公路收费定价模式包括基于级差效益的定价模式和基于成本的定价模式。基于级差效益的定价模式考虑的是道路使用者的利益，目的是让道路使用者通过支付通行费用换取运输量增加、运输成本降低、运行距离减少、运行时间节约等道路使用效益。基于此种模式，陈传德等[5]考虑了车辆在途时间、维修保养费用等因素，对高速公路的收费定价进行计算；安乔治等[6]将道路使用者的收益影响因素分为时间节省、油耗降低和安全性提高三个方面，构建了高速公路收费定价模型。基于成本的定价模式考虑的是道路经营者的利益，目的是为了实现道路建设项目及运营的收支平衡[7]。基于此种模式，曾光辉[8]对高速公路的建设、运营和养护成本以及投资收益进行分析，设计了高速公路基准收费定价模型。单一的定价模式仅考虑了道路使用者或出行者其中一方的利益，为了考虑多个主体的利益，Li等[9]、张欢等[10]、魏连雨等[11]建立了双层规划模型来描述高速公路的收费定价问题。

在差异化收费研究方面，现有的方案大多面向单一场景。为了缓解高峰期拥堵问题，李金华等[12]和刘伟铭等[13]分别基于消费者均衡理论和瓶颈模型，设计了重大节假日期间高速公路阶梯式收费定价方案；李明[14]提出对一天当中两个道路拥堵时段的高速公路通行费率进行降价调整；针对路段拥堵问题，Lee [15]基于道路饱和度指标对高速公路拥堵路段区间进行筛选，制定分路段差异化收费策略；还有一些学者侧重设计分车型的差异化收费方案，王玉彤[16]和申科等[17]根据不同车型车辆对成本变化的敏感性，制定分车型差异化收费方案；王海兰等[18]和Figueiras等[19]为实现物流企业降本，专门设计了针对货车的差異化收费定价方案。

现有的高速公路收费方案往往难以同时满足道路使用者、经营者等多方的利益需求，且相关研究往往只针对某一种场景，缺少对多模式、适用性强的差异化收费定价方案进行设计。为了进一步完善高速公路差异化收费方案，本文考虑道路经营者和使用者两方面的利益，以增加高速公路运营效益和实现路网多用户随机均衡分配为目标，建立基于双层规划模型的高速公路差异化收费定价模型，设计模型求解算法，并制定一套分路段、分出入口、分时段、分车型的高速公路差异化收费方案，方案对于提高高速公路竞争力，促进路网交通流合理分布，提升高速公路运营收益有重要意义。

1 研究方法

1.1 差异化收费定价模型

差异化收费定价问题中，道路经营者和使用者是双层决策者，二者间具有领导和跟随关系，其中，道路经营者是上层领导决策者，根据一定的目标确定通行费率，道路使用者是下层跟随决策者，基于领导者制定的价格，综合考虑行程时间等因素做出路径选择。领导者的决策会影响跟随者的选择，而跟随者的决策又会反馈给领导者，在上下层决策相互作用、不断迭代优化的过程中，形成最优的差异化收费定价方案。为了充分发挥差异化收费的价格杠杆作用，实现通行费率降低、交通流分配优化、运输效率和质量提升的目的，本文同时考虑道路经营者和使用者利益，设计双层规划模型进行差异化收费定价。

1.1.1 上层规划

对于经营性高速公路的运营方而言，通行收费是维持公路后期养护和运营的关键。为了保证高速公路的正常运行以及高速公路运营企业的生产生存，将实现高速公路运营方收益增加作为定价模型的上层规划目标。高速公路运营方的收益由收费总收入、道路养护成本、环境治理成本、管理运营成本和设备成本构成，计算公式如下：

Smax=SN－SA，（1）

SN=SR－SM－SE－SO－SD，（2）

s. t.   SN≥SA ，（3）

其中，S为差异化收费定价方案实施后高速公路运营方收益的变化量，单位为万元/年；SN为施行差异化收费方案后高速公路运营方的收益；SA为施行差异化收费方案前高速公路运营方的收益；SR为高速公路收费总收入；SM为道路养护成本；SE为环境治理成本；SO为管理运营成本；SD为设备运行成本。

（1）高速公路收费总收入

其中，I为车型集合，根据交通运输部最新修订的《收费公路车辆通行费车型分类》（JT/T 489-2019）[20]划分，详情见表1；J为高速路段集合；T为通行时段集合，包括客车通行高峰时段和平峰时段；fi，j为路段j上车型i的通行费率，qi，j为路段j上车型i的交通流量，Lj为路段j的长度，Cj为路段j的通行能力。

（2）道路养护成本

其中，MO为日常养护成本；MR为中、大修均摊成本；FMO，j为路段j的养护费用，据调研，山东省高速公路单车道的日常养护费用为1.5万元/km；lj为路段j的车道数；k1为通车年限系数，通车第3年取1，之后每增加1年调增8％；k2为地形地貌系数，平原微丘区路段取1，山岭重丘区路段取1.1；k3为通行费收入系数，每车道每公里年通行费收入在62.5万元以下取1，在62.5万元～125万元取1.1，高于125万元取1.15；k4为交通量系数，每车道年平均日交通量小于6 250辆取1， 6250～10 000辆取1.2，高于10 000辆取1.3；FMR，j为路段j的中、大修费用，据调研，FMR，j取每10年100万元/km。

（3）环境治理成本

其中，fp为标准车型的环境治理费用，单位为元/公里，取值范围一般为0.06～0.08元/km[21]；kp为标准车型折算系数。

（4）管理运营成本

其中，fO为管理运营费用，包括管理、养护人员工资等费用，据调研，fp取35万元/（km·a）。

（5）设备成本

其中，fD为设备支出费用，包括监控设备购买与安装费用、电费等，据调研，fD取10万元/（km·a）。

1.1.2 下层规划

模型的下层规划目标是实现路网多用户随机均衡分配，即各车型出行者均不能通过单方面改变路径来降低估计的路段阻抗。定义一个广义费用描述路段阻抗，广义费用由时间成本和费率成本两部分组成，计算公式如下：

其中，ri，l为车型i选择路径l的广义费用，单位为元；vi为车型i的时间价值，单位为元/min；

Oi为车型i的百公里燃油费用，单位为元；Fi为车型i的百公里油耗量，单位为L；Pf为燃油的月平均价格，单位为元/L；tj为路段j的行程时间；tj，0路段j的自由流行驶时间；α、β为阻滞系数，分别取0.15和4[22]。

出行者路径感知阻抗的随机误差项服从Gumbel分布，令感知阻抗的负值为路径的效用，基于最大效用理论，各车型出行者基于logit模型进行路径选择。则下层规划实现多用户随机均衡的条件如下[23]：

其中，di（r，s）为车型i在r和s间的OD交通量；pi，l（r，s）为车型i选择路径l的概率。

根据变分不等式理论，多用户随机均衡分配问题等价于求一个可行路径流量，使以下变分不等式成立：

其中，q（r，s）*为所求的路径流量解；Ωq（r，s）为可行路径流量集合。

Ωq（r，s）满足的约束条件如下：

其中，δj，l（r，s）为路段-路径相关变量，若路段j属于路径l，则δj，l（r，s）=1，否则δj，l（r，s）=0。

由于变分不等式模型的可行域由线性和非负约束条件构成，因此Ωq（r，s）是紧凸集，且路段阻抗函数ri（r，s）在Ωq（r，s）上是随交通量变化的严格单调递增连续函数，因此存在并且具有唯一的解。

1.2 模型求解算法

基于双层规划的差异化收费定价问题属于非确定性多项式困难问题，使用精确算法求解难度很大且需要花费大量时间，通常使用启发式算法进行求解。考虑到启发式算法求解得到的是近似最优解，本文分别使用遗传算法（genetic algorithm，GA）和模拟退火（simulated annealing，SA）算法与下层规划求解算法进行组合进行求解。

1.2.1 遗传算法求解步骤

第一步：将各车型通行费率的折扣率设为候选解，考虑实际情况将折扣率的取值范围定为[0，10%]，使用二进制编码法生成规模为20的初始种群，设置最大迭代次数为50次，令初始迭代次数k=1；

第二步：基于种群中每个个体计算各车型通行费率，代入下层规划求解交通流分配结果，将高速公路运营收益增量作为适应度函数，计算每个个体的适应度；

第三步：使用轮转法进行个体选择，选择概率为个体适应度在种群总適应度中的占比；使用单点变异进行交叉运算，交叉概率设为0.6；使用二进制变异进行变异运算，变异概率设为0.08，生成新种群；

第四步：若k>50，解码输出最优个体对应的折扣率，否则令k=k+1，返回第二步。

1.2.2 模拟退火算法（SA）求解步骤

第一步：设置初始温度Ts为100，终止温度Te为0，温度下降比例为0.95，内层循环次数为50，将现行初始费率代入下层规划，求解得到初始交通流分配结果，计算初始收益增值，令外层循环次数m=1，内层循环次数n=1；

第二步：在当前温度Tm下，以[0，10%]为折扣区间更新费率，代入下层规划，计算新的收益增值，令n=n+1；

第四步：若n>50，转到第五步，否则返回第二步；

第五步：若Tm

1.2.3 下层规划求解算法

下层规划实现多用户随机均衡分配，采用迭代加权法（method of successive algorithm，MSA）进行求解。

第一步：按照各路段的初始阻抗对各车型的交通需求执行随机加载，得到各路段的初始混合交通流量xj，0，令循环次数m=1；

第二步：基于各路段当前的混合交通流量xj，m，使用广义费用函数计算各路段阻抗；

第三步：基于新的路段阻抗，使用Dial算法对各车型的交通需求执行logit加载，得到各路段的附加混合交通量yj，m；

第四步：使用MSA法计算各路段当前的混合交通量

2 研究区域

本次研究的区域为山东省东北部地区，在现有行政区划的基础上，将研究区域划分为16个交通小区，信息如表2所示。

各小区间的OD数据从山东省2021年高速公路联网收费数据以及路段卡口数据中提取得到。研究区域内的主要路段包括龙青高速青岛段，以及3条与其平行的国省道，分别是G204烟沪线莱西至城阳段、S209蓬黄线莱阳至即墨段、S213龙青线莱西至即墨段。

龙青高速研究路段全长78.10 km，起至莱西东收费站，终点为城阳收费站，由北向南途径6个收费站，按收费站将龙青高速划分为7个出入口段。龙青高速各路段和平行国省道两个方向的交通量和交通饱和度VC比（即：最大交通量V /最大通行能力C）如图2所示。

由图2可知，两个方向的交通流在高速公路和平行国省道上的分布情况具有一定的相似性。具体而言，龙青高速路段H_3、H_7双向的年平均日交通流量高于平行国省道，为国省道分担了一部分的交通压力；而高速路段H_1、H_2、H_4、H_5、H_6的交通流量都低于平行国省道，且国省道承担了较大的交通流量，路段交通饱和度数值较大，道路资源不能充分满足路段的交通需求，交通运行效率将受到影响，面临拥堵的问题。因此本文以龙青高速北向南方向为代表，对交通流量低于平行国省道，且平行国省道交通饱和度比较大的高速公路路段H_1、H_2、H_4、H_5的通行费率进行调整。

为了提高货物运输效率，节约物流运输成本，本文还考虑对高速公路两轴以上货车（即3～6类货车）的通行费率进行进一步调整。首先对高速公路客车通行交通量时变情况进行统计，结果如图3所示。

由图3可知，高速公路客车车辆主要集中在6：00—18：00间出行，且经过统计，这一时段客车通行量在一天通行量当中占比为60%以上。为了在吸引中、大型货车选择高速公路的同时，减少货车对高速公路高峰时期客车运行的影响，本文以60%的比例为节点，将日均出行交通量划分为高峰出行交通量和平峰出行交通量，运用双层规划模型对出行平峰期两轴以上货车的通行费率进行调整，进一步完善分时段、分车型的差异化收费定价方案。

3 龙青高速差异化收费方案设计

山东省高速公路现行通行费率以及各车型收费系数如表3所示。

基于现状各车型在OD间对高速公路和国省道的选择结果，使用极大似然估计方法对各车型的时间价值Vi进行标定，结果如表4所示。

首先保持各车型间的收费系数不变，对需要调整费率的龙青高速路段H_1、H_2、H_4、H_5进行排列组合，制定15种不同的分出入口差异化收费方案，使用第一节提出的双层规划模型以及两种求解算法进行求解，得到每种方案的高速公路运营方年收益增值以及最优费率调整幅度，结果如图4所示。

由图4可知，基于两种算法求解得到高速公路收益增值及对应的最优折扣率结果具有一定的相似性，验证了近似最优解的可信度。同时发现方案4、6、7、12实施后不满足上层规划中高速公路收益增值必须为正的约束条件，将这4个方案剔除。在此基础上，进一步调整两轴以上货车在当日18：00至第二天6：00这一平峰时段的通行费率，11种方案中有5种方案能够使高速公路收益得到进一步提升。

随着高速公路通行费率的调整，道路阻抗发生变化，出行者重新进行路径选择，其出行时间、燃油费用和通行费率构成的出行成本也随之改变。为了从5种备选方案中选出效益最优的方案，对差异化实施前后路网交通流的出行成本差值进行计算，计算公式如下：

其中，D为出行成本降低量，单位为万元/年；ri，j为方案实施前车型i在路段j上的广义费用；qi，j为方案实施前路段j上车型i的交通流量；ri，j′为方案实施后车型i在路段j上的广义费用；qi，j′为方案实施后路段j上车型i的交通流量。

经过计算，得到5种备选方案实施后的效益如表5所示。

由表5可知，方案14实施后能够使龙青高速运营方的年收益提升最多，增加了786.19万元，同时使道路使用者出行成本降低716.51万元/年，将其作为最终的差异化收费定价方案，具体方案是在6：00—18：00客车出行高峰时段，对路段H_2、H_4、H_5各车型的通行費率降价2%，并在此基础上，再给予当日18：00至第二天6：00平峰时段出行的两轴以上货车降价3%。龙青高速北向南方向各车型在高峰和平峰时段的通行费率如表6所示。

4 结语

本文通过建立双层规划模型描述了道路经营者和使用者对高速公路收费定价的共同决策作用，对高速公路差异化收费问题进行研究。模型上层规划考虑了高速公路收费总收入、养护成本、环境治理成本、管理运营成本等多个因素，以实现高速公路运营收益增加为目标，下层规划考虑了道路使用者的时间成本和费用成本，以实现路网多用户随机均衡分配为目标。在分析路网交通流时空分布特征的基础上，利用设计的模型有针对性地为山东省龙青高速青岛段制定了分出入口路段、分时段、分车型的差异化收费方案，其中最优收费方案能使龙青高速在北向南方向上的年收益增加786.19万元，路网用户出行成本降低716.51万元。研究结果进一步完善了多模式差异化收费方案，促进了方案的实施与推广，使路网资源得到更加合理的配置，有效减轻平行国省道的交通负担，同时也为高速公路差异化收费方案的制定提供理论支持和参考依据。

参考文献：

［1］林文新， 王建伟， 林渝钧. 基于养护成本的高速公路收费费率问题研究[J]. 交通运输系统工程与信息， 2013， 13（5）： 145-149. DOI： 10.16097/j.cnki.1009-6744.2013.05.007.

[2]ABULIBDEH A， ZAIDAN E. Analysis of factors affecting willingness to pay for high-occupancy-toll lanes： Results from stated-preference survey of travelers[J]. Journal of Transport Geography， 2018， 66： 91-105. DOI： 10.1016/j.jtrangeo.2017.11.015.

[3]金雪晴. 可持续发展条件下高速公路收费费率研究[D]. 重庆： 重庆交通大学， 2018.

[4]吴晓东. 考虑车流量变化的经营性高速公路定价策略研究[D]. 杭州： 浙江大学， 2019.

[5]陈传德， 赵文义. 基于级差效益的公路收费定价模型[J]. 长安大学学报（自然科学版）， 2009， 29（4）： 39-42. DOI： 10.19721/j.cnki.1671-8879.2009.04.009.

[6]安乔治， 唐洁. 基于受益角度的京津冀高速公路收费定价模型构建[J]. 价格月刊， 2016（12）： 15-18. DOI： 10.14076/j.issn.1006-2025.2016.12.03.

[7]孙如龙， 陆正峰， 速鸣， 等. 高速公路收费定价模式分析及建议[J]. 交通企业管理， 2020， 35（1）： 37-41. DOI： 10.3963/j.issn.1006-8864.2020.01.012.

[8]曾光辉. 高速公路市场化经营模式下的政府定价方法[J]. 粤港澳市场与价格， 2009（4）： 10-14.

[9]LI T F， SUN H J， WU J J， et al. Optimal toll of new highway in the equilibrium framework of heterogeneous households′ residential location choice[J]. Transportation Research Part A： Policy and Practice， 2017， 105： 123-137. DOI： 10.1016/j.tra.2017.08.012.

[10]张欢， 史峰， 卢毅， 等. 弹性需求下高速公路超限补偿费率优化模型[J]. 中国公路学报， 2012， 25（4）： 126-132. DOI： 10.19721/j.cnki.1001-7372.2012.04.018.

[11]魏连雨， 李壮. 基于路网特征的高速公路计重收费费率确定[J]. 重庆交通大学学报（自然科学版）， 2014， 33（6）： 122-126. DOI： 10.3969/j.issn.1674-0696.2014.06.26.

[12]李金华， 吕相舟， 周思远， 等. 缓解高速公路拥堵的消费者均衡模型研究[J]. 工业技术经济， 2018， 37（6）： 100-105. DOI： 10.3969/j.issn.1004-910X.2018.06.013.

[13]刘伟铭， 陈纲梅. 基于阶梯函数的节假日高速公路拥堵收费和过渡收费模型[J]. 广西大学学报（自然科学版）， 2018， 43（5）： 1912-1920. DOI： 10.13624/j.cnki.issn.1001-7445.2018.1912.

[14]李明. BOT运营模式的高速公路货车多维度差异收费决策方法研究[D]. 西安： 长安大学， 2019.

[15]LEE E， KIM D K， KHO S Y， et al. Segment-based differentiated pricing strategy for reducing congestion of expressways[J]. Journal of Korean Society of Transportation， 2014， 32（6）： 675-685. DOI： 10.7470/jkst.2014.32.6.675.

[16]王玉彤. 高速公路货运车辆差异化收费方案研究[D]. 石家庄： 石家庄铁道大学， 2020.

[17]申科， 段莉珍， 李洁云， 等. 高速公路收费新标准下货车车型收费系数测算[J]. 公路与汽运， 2021（3）： 24-29. DOI： 10.3969/j.issn.1671-2668.2021.03.006.

[18]王海兰， 郑彦军. 基于运输货类的货运车辆收费费率调整分析[J]. 公路， 2015， 60（9）： 195-199.

[19]FIGUEIRAS P， GONALVES D， COSTA R， et al. Novel Big Data-supported dynamic toll charging system： Impact assessment on Portugal′s shadow-toll highways[J]. Computers & Industrial Engineering， 2019， 135： 476-491. DOI： 10.1016/j.cie.2019.06.043.

[20]中華人民共和国交通运输部. 收费公路车辆通行费车型分类： JT/T 489-2019[S].北京：中国标准出版社，2019.

[21]闫丹丹. 基于两部制的高速公路收费定价研究[D]. 昆明： 昆明理工大学， 2021.

[22]邵春福. 交通规划原理[M]. 北京： 中国铁道出版社， 2004.

[23]徐兵. 多用户多准则随机交通均衡理论与应用研究：基于变分不等式方法[D]. 上海： 复旦大学， 2006.