局部阴影下光伏阵列最大功率点跟踪算法的研究

刘晨 黄翼虎

摘要：传统的最大功率点跟踪（MPPT）算法在光伏阵列多峰情况下容易陷入局部最优，蝴蝶优化算法有全局优化能力，但由于收敛精度较低而没有被广泛使用。提出了一种改进蝴蝶优化算法与扰动观察法相结合的MPPT算法，引入混沌映射理论和动态切换概率改进蝴蝶优化算法。先通过蝴蝶优化算法的全局搜索能力定位最大功率点范围，后切换小步长扰动观察法精准定位最大功率点。混合算法结合了蝴蝶优化算法和扰动观察法的优点，通过Simulink仿真实验，与传统蝴蝶优化算法、粒子群算法作对比，改进后的算法能够适应复杂多变的光照环境，且在收敛精度和速度方面均有一定优势。

关键词：光伏发电；最大功率点跟踪；蝴蝶优化算法；扰动观察法；混沌映射

中图分类号：TM615   文献标志码：A   文章编号：1002-4026（2023）05-0044-08

Maximum power point tracking algorithm for photovoltaic arrays under local shadow

LIU Chen，HUANG Yihu

（College of Automation and Electronic Engineering， Qingdao University of Science and Technology， Qingdao 266061， China）

Abstract∶The traditional maximum power point tracking （MPPT） algorithm is prone to fall into local optimization in the case of a multipeak photovoltaic array. The butterfly optimization algorithm has a strong global search capability and a relatively stable convergence process; however， it has not been widely used due to its low convergence accuracy. This paper proposes an MPPT algorithm that combines the improved butterfly optimization algorithm with the perturbation and observation method. The traditional butterfly optimization algorithm was optimized by introducing the chaotic mapping theory to improve the distribution of the initial butterfly population. Besides， the dynamic switching probability was used to optimize the switching strategy. Herein， first， the global search capability of the butterfly optimization algorithm was used to locate the range of the maximum power point， and then the small step size perturbation and disturbance observation method were used to accurately locate the maximum power point. This algorithm combines the advantages of the global optimization of the butterfly optimization algorithm and the precise optimization of the perturbation and observation method. Furthermore， Simulink simulation experiments were conducted， and the results were compared with the traditional butterfly optimization algorithm and particle swarm optimization algorithm. The results show that the improved algorithm can adapt to complex and changing light conditions and has certain advantages in both convergence accuracy and speed.

Key words∶photovoltaic power generation; maximum power point tracking; butterfly optimization algorithm; perturbation and observation method; chaotic mapping

科技的發展能够提高人们的生活水平和改善人们的生活方式，但由此导致对能源（特别是电能）的可靠性要求和需求量大幅提高[1]，传统化石能源对生态环境的破坏不能满足未来的发展要求。光伏发电是一种绿色环保的发电方式，因其发电过程中没有污染物产生和碳排放，符合国家政策和未来发展的需要，是未来能源供应的重要一环。光伏阵列的最大功率点容易受光伏阵列所处环境的影响，若外界环境变化时不能及时地做出相应的调整，则光伏电池的能源转换效率降低。

开路电压法[2]、扰动观察法[3]、电导增量法等传统的最大功率点跟踪算法收敛速度慢且存在振荡，容易陷入局部最优。粒子群算法（particle swarm optimization， PSO）[4]、布谷鸟算法[5]、蚁群算法[6]等群智能算法虽然能够进行有效的全局寻优，但缺乏收敛精度和速度。蝴蝶优化算法（butterfly optimization algorithm，BOA）具有强大的全局搜索能力[7]，为了提高蝴蝶优化算法的最大功率点跟踪（maximum power point tracking，MPPT）性能，本文引入混沌映射理论和动态切换策略优化传统的蝴蝶优化算法，提出了一种将扰动观察法和蝴蝶优化算法相结合的复合型MPPT算法，该算法启动时先采用蝴蝶优化算法进行全局寻优和局部寻优[8]，直到光伏电池达到最大功率点附近，后采用小步长扰动观察法精确跟踪到最大功率点[9]。采用Matlab/Simulink模拟光伏阵列在多种光照条件下的输出特性，通过仿真与粒子群算法和传统蝴蝶优化算法对比，验证了改进型蝴蝶优化算法在光伏发电MPPT中的优越性。

1 光伏发电系统

1.1 光伏电池的建模

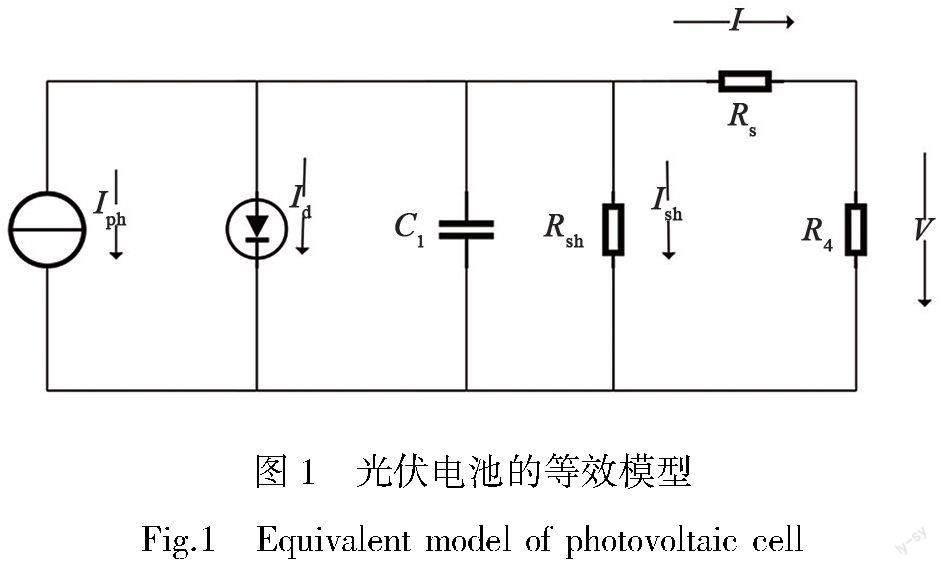
光伏发电是利用了半导体的光电效应：光能直接转变为电能的一种技术[10]。光伏电池的等效电路如图1所示。[JP]光伏电池的输出特性方程见公式（1）～（4），式中的物理量含义见表1，这些变量受光照强度和温度变化的影响，其中光伏电池内部的串联电阻Rs可忽略不计。

1.2 遮阴情况下的光伏电池输出特性

在自然条件下遮阴问题的存在使光伏阵列的各个光伏组件处于不同的光照条件下，此时会产生“热板效应”，影响甚至破坏光伏组件。光伏电池并联旁路二极管[11]可以避免“热板效应”，却造成了光伏模组输出功率的多峰值，影响传统MPPT算法的精度。

1.3 不同环境下光伏电池的输出特性

本文采用5块串联光伏电池构成光伏阵列，每块光伏电池由4×2光伏组件构成。光伏组件的电气参数如下：开路电压36.60 V，短路电流7.84 A，最大功率点电压29 V，最大功率点电流7.35 A。为了分析外界复杂的环境，分别设置3种不同的光照模式，见表2。模式1～3分别模拟了光伏阵列在恒定光照、阴影环境、动态阴影这3种情况[12]。根据光伏电池的数学型，本文搭建了光伏电池模型，保持输入温度t=25 ℃不变，仿真分析不同光照环境光伏阵列的输出特性，输出P-V曲线如图2所示。

2 IBOA-P&O在MPPT中的应用

2.1 扰动观察法

扰动观察法（perturb and observe algorithms， P&O）是最经典的MPPT算法，也是目前应用最广的MPPT算法。给光伏电池输出电压施加一个微小的代数增量（增量可为负值），判断此时光伏电池输出功率在最大功率点的方位，从而进一步改变光伏电池输出功率[13]。若光伏模组的输出功率的变化量为正，则继续向这个代数增量的正方向添加扰动；若光伏模组的输出功率的变化量为负则反之，直到光伏电池的输出功率工作在最大功率点附近。

2.2 蝴蝶优化算法

蝴蝶优化算法（BOA）是元启发式智能算法的一种。该算法从蝴蝶群体的日常生理活动中得到启发。在观察蝴蝶交配行为时发现蝴蝶存在一种器官能感受到其他蝴蝶在空气中释放的激素，也就是香味，蝴蝶通过香味的浓度来判断其他蝴蝶的位置。当蝴蝶移动时，其释放出的香味浓度发生变化，其他蝴蝶通过器官感知某一区域的香味的浓度来判断是否有同伙在此区域，若蝴蝶感受某一区域的香味浓度高，则向这一区域蝴蝶靠近，这就是全局搜索。若感受不到浓度更高的香味时，则随机移动，这就是局部搜索[14]。香味计算公式如式（5）所示：

f=cSa。（5）

蝴蝶的香味由幂指数a、感觉因子c和刺激强度S决定。其中适应度决定了蝴蝶收到的刺激的强度[15]。该算法有两个阶段，即全局搜索阶段和局部搜索阶段，可表示为：

g*表示适应度更高的蝴蝶，k和j表示随机选择的第k只和第j只蝴蝶。设置P切换全局搜索和局部搜索。迭代时用随机数r与设定的切换概率P对比，选择算法进行全局搜索还是局部搜索[16]。

r=rand（0，1）。（8）

2.3 改进型蝴蝶优化算法

2.3.1 Tent映射初始化

由于BOA在搜索空间内采用随机策略初始化蝴蝶种群位置，可能会导致蝴蝶个体分布不均匀，从而造成算法过早收敛，陷入局部最优。Tent混沌映射结构简单，且具有遍历性的特点[17]，为了解决上述问题，本文引入Tent混沌映射对蝴蝶个体位置初始化，使蝴蝶种群均匀地分布在搜索空间中，有利于算法初期在空间内进行更好地搜索，提高了算法的精度。

当u=0.5时，Tent混沌映射最典型，所得的序列具有均匀分布的特性。此时Tent混沌映射的公式为：

2.3.2 动态切换策略

BOA在搜索过程中分为全局搜索和局部搜索，算法迭代过程中过多的全局搜索会导致算法收敛时间过长，影响收敛精度；若过多地进行局部搜索则可能导致算法过早收敛，容易陷入局部最优。本文提出了一种动态切换概率Pi的控制策略，迭代时Pi与0.6对比，选择进行全局搜索还是局部搜索。公式为：

式中的P0= 0.65；N为算法最大迭代次数，n为当前迭代次数，r为[0，1]区间内的随机数。在算法迭代前期使全局搜索的概率大于局部搜索，算法迭代后期局部搜索概率大于全局搜索。动态切换策略在不影响算法随机性的前提下进一步提升了算法的精度和收敛速度。

2.4 IBOA-P&O的復合控制策略

传统的BOA因其算法公式较少、结构特殊、能够跳出局部最优而被广泛应用，其在解决光伏阵列因遮阴产生的多峰问题上具有优越性，但收敛精度低和收敛速度慢仍是该算法等群智能算法的通病。本文通过引入混沌映射理论和动态切换概率对蝴蝶优化算法进行改良（以下简称IBOA），并与扰动观察法结合的策略解决上述问题。在全局范围先采用蝴蝶优化算法进行全局寻优对最大功率点定位，当蝴蝶间距小于设定值时切换为小步长扰动观察法对MPPT精准定位。

算法流程图如图3，具体步骤如下：

（1）初始化蝴蝶种群位置和参数；

（2）以光伏阵列输出功率作为适应度函数，计算当前位置各个蝴蝶的适应度；

（3）依据公式（10）～（12）更新位置，寻找最大功率点；

（4）判断是否锁定最大功率点范围或达到最大迭代次数；

（5）切换小步长扰动观察法直至搜索到最大功率点。

3 仿真分析

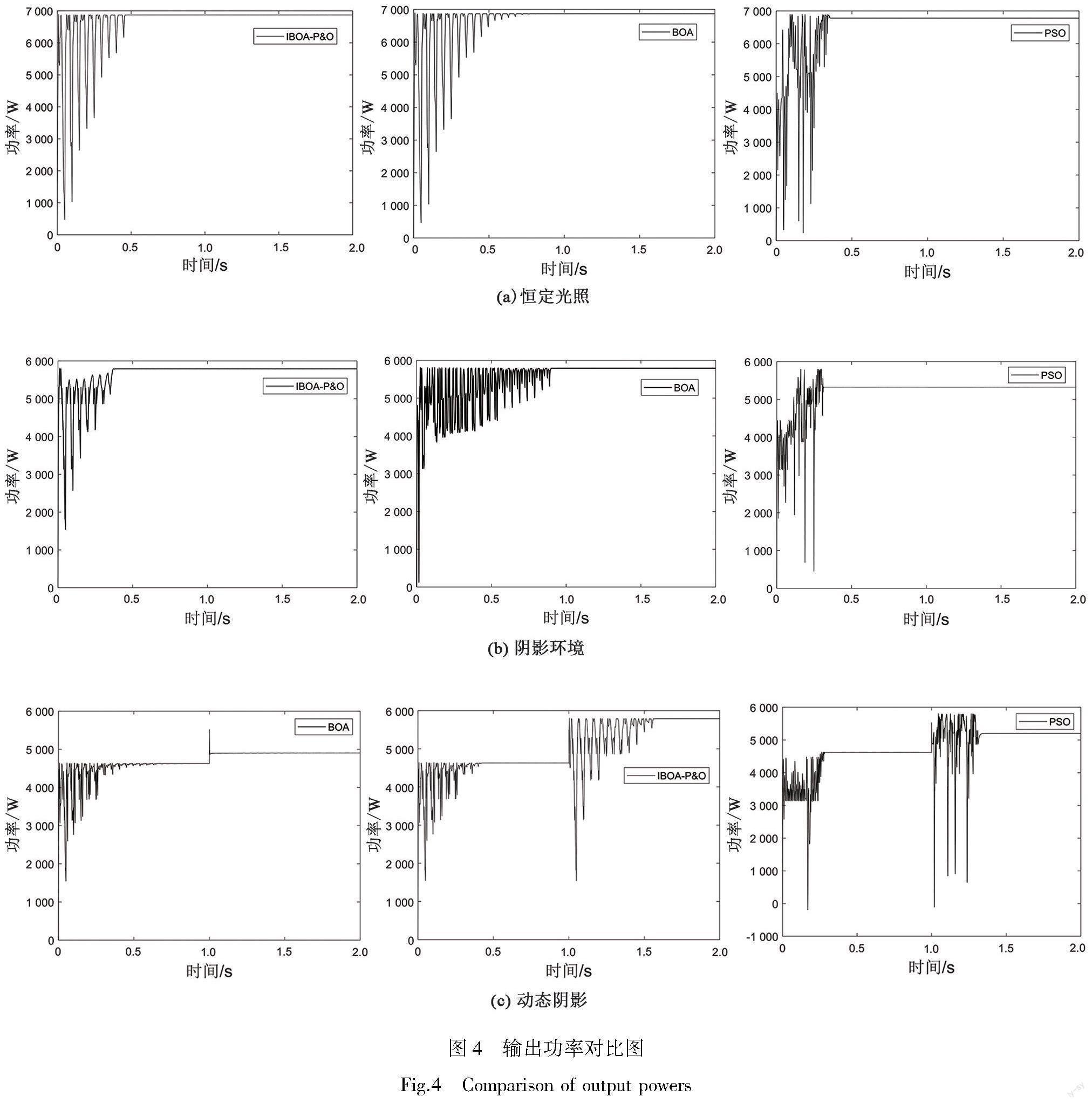
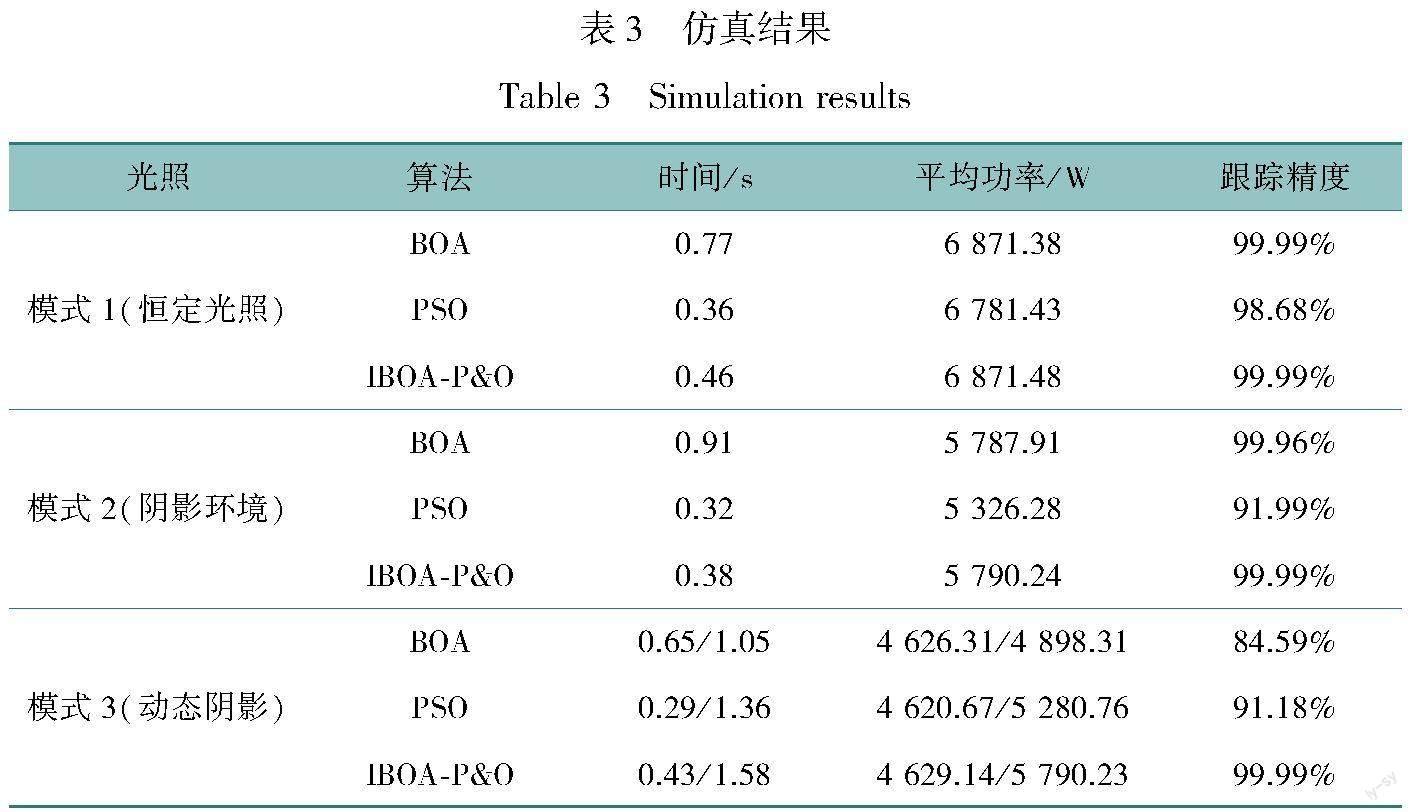
本文采用Matlab/Simulink平台对光伏阵列MPPT仿真以验证改进蝴蝶优化算法的優越性。仿真环境选取在温度25 ℃，分别使光伏模组在模式1（无遮阴）、模式2（局部遮阴）和模式3（变化阴影）这3个条件下进行仿真实验，建立粒子群算法（PSO）、传统蝴蝶优化算法（BOA）和改进型蝴蝶优化算法（IBOA-P&O）的MPPT模块，对这3个环境下仿真结果进行分析仿真，结果见图4及表3。

环境温度25 ℃，光照模式为模式1时，光伏阵列的输出特性曲线见图4（a）。传统BOA算法在0.77 s寻找到最大功率点，其最大输出功率为6 871 W；采用PSO算法的光伏阵列在0.36 s时寻找到最大功率点，其最大输出功率约为6 781 W；IBOA-P&O算法在0.46 s寻找到最大功率点，其最大输出功率为6 872 W。多块光伏电池组成的光伏阵列在光照和温度恒定的情况下，3种算法都能够较为精确的寻找到最大功率点。传统BOA算法收敛速度最慢；IBOA-P&O算法在收敛速度稍逊PSO算法，但在收敛过程中系统的稳定性要优于PSO算法且收敛精度最高。PSO算法因其随机性较强且收敛稳定性差，故认为结构简单且稳定的IBOA-P&O算法更适合用作MPPT算法。

环境温度为25 ℃，光照模式为模式2，光伏阵列输出功率曲线见图4（b）。传统BOA算法在0.91 s寻找到最大功率点，其最大输出功率为5 788 W。采用PSO算法的光伏阵列在0.32 s时寻找到最大功率点，其最大输出功率为5 326 W；IBOA-P&O算法在0.38 s寻找到最大功率点，其最大输出功率为5 790 W。光伏阵列因遮阴导致输出特性多峰值时，传统BOA算法收敛速度过慢；PSO算法在寻优速度快于IBOA-P&O算法但其跟踪精度远低于IBOA-P&O算法，且系统稳定性低；而IBOA-P&O算法虽然收敛时间略长但MPPT精度最高。因此在处理光伏阵列因遮阴产生的输出功率多峰值问题时IBOA-P&O算法更为合适。

环境温度为25 ℃，光照模式从模式2变为模式3时，光伏阵列输出功率曲线见图4（c）。当光照条件发生突变时传统BOA算法陷入局部最优；PSO算法在收敛时间上优于IBOA-P&O算法但其跟踪效率远低于IBOA-P&O算法，系统稳定性相对也较差，因此在处理变化阴影问题上IBOA-P&O算法更加合适。

综上所述，传统BOA算法收敛时间过长且易陷入局部最优；PSO算法在全局寻优中寻优速度较快，但因其精度低、系统稳定性差、寻优随机性大并不能更加准确的寻找到最大功率点；IBOA-P&O算法既可以快速地进行全局寻优，又可以准确地寻找到最大功率点，相比以上两种算法，更适合用作MPPT算法。

4 结论

本文提出的蝴蝶优化算法和扰动观察法相结合的MPPT算法解决了蝴蝶优化算法寻优精度低和扰动观察法不能进行有效的全局寻优的问题。通过仿真分析3种MPPT算法在不同环境下的输出特性，通过对比表明了改进型蝴蝶优化算法在光伏发电MPPT的优越性。改进型蝴蝶优化算法在MPPT精度和系统稳定性上较于其他两种算法有明显的优势，在光伏阵列阴影变化时更能明显体现出此算法的高精度性。

参考文献：

［1］裴婷婷. 光伏发电系统中光伏阵列的故障诊断与配置重构策略研究[D].兰州： 兰州理工大学， 2020.

[2]钟长艺， 康龙云， 聂洪涛， 等. 基于开路电压法光伏电池最大功率追踪器[J]. 电力电子技术， 2011， 45（7）： 103-105. DOI： 10.3969/j.issn.1000-100X.2011.07.038.

[3]刘军， 王得发， 薛蓉. 光伏发电系统MPPT控制方法的研究及改进[J]. 电子测量技术， 2016， 39（5）： 10-13. DOI： 10.19651/j.cnki.emt.2016.05.003.

[4]韩思鹏， 蒋晓艳， 罗意， 等. 遮阴条件下光伏MPPT自适应粒子群算法优化[J]. 太阳能学报， 2022， 43（6）： 99-105. DOI： 10.19912/j.0254-0096.tynxb.2020-1001.

[5]王洪亮， 周于尧， 刘志坚， 等. 基于改进CS算法的光伏系统MPPT仿真研究[J]. 电子测量技术， 2020， 43（7）： 67-71. DOI： 10.19651/j.cnki.emt.1903795.

[6]王朱锁， 张军朝， 张俊虎， 等. 基于DSP的改进蚁群二阶段MPPT控制器设计[J]. 电子器件， 2019， 42（6）： 1399-1404. DOI： 10.3969/j.issn.1005-9490.2019.06.010.

[7]高文欣， 刘升， 肖子雅， 等. 全局优化的蝴蝶优化算法[J]. 计算机应用研究， 2020， 37（10）： 2966-2970. DOI： 10.19734/j.issn.1001-3695.2019.07.0274.

[8]郭德龙， 周锦程， 周永权. 基于Levy飞行改进蝴蝶优化算法[J]. 数学的实践与认识， 2021， 51（12）： 130-137.

[9]杨海柱， 岳刚伟， 康乐. 基于粒子群优化算法和电导增量法的多峰值MPPT控制[J]. 电源学报， 2019， 17（6）： 128-136. DOI： 10.13234/j.issn.2095-2805.2019.6.128.

[10]张鹏. 局部遮阴情况下光伏阵列最大功率点跟踪技术研究[D]. 济南： 山东大学， 2021.

[11]王青云. 光伏微网失配分析与智能MPPT控制[D]. 杭州： 杭州电子科技大学， 2022.

[12]郭昆丽， 刘璐雨， 蔡维正. 基于混合算法的光伏多峰值MPPT研究[J]. 电源技术， 2021， 45（8）： 1040-1043. DOI： 10.3969/j.issn.1002-087X.2021.08.022.

[13]易磊， 谢雨龙， 曾凡炎， 等. 基于神经网络的改进扰动观察法MPPT控制[J]. 太阳能学报， 2022， 43（4）： 198-203. DOI： 10.19912/j.0254-0096.tynxb.2020-0803.

[14]李田来， 刘方爱. 带混沌映射的WSN蝴蝶优化定位算法[J]. 计算机工程与设计， 2019， 40（6）： 1729-1733. DOI： 10.16208/j.issn1000-7024.2019.06.040.

[15]王依柔， 张达敏， 徐航， 等. 基于自适应扰动的疯狂蝴蝶算法[J]. 计算机应用研究， 2020， 37（11）： 3276-3280. DOI： 10.19734/j.issn.1001-3695.2019.08.0281.

[16]尹晓叶. 基于传统BOA的新型自适应蝶形优化算法设计[J]. 电子技术与软件工程， 2019（12）： 166.

[17]滕志军， 吕金玲， 郭力文， 等. 一种基于Tent映射的混合灰狼优化的改进算法[J]. 哈尔滨工业大学学报， 2018， 50（11）： 40-49. DOI： 10.11918/j.issn.0367-6234.201806096.