借助直观教学 有效落实四基

何贺辉

《义务教育数学课程标准（2011年版）》将义务教育阶段的数学课程总目标由“双基”发展成“四基”，即获得适应社会生活和进一步发展所必须的数学的基本知识、基本技能、基本思想和基本数学经验。朱智贤在《儿童心理学》一书中指出：小学生思维的特点是以具体形象思维为主要形式逐步过渡到以抽象思维为主要形式，但这种抽象逻辑思维在很大程度上仍然是与直接和感性经验相联系的，仍然有很大成分的具体形象性。小学生对问题的理解往往还停留在表面，抽象思维能力差，所以，充分借助直观教学是有效落实四基的方法。

• 数形结合，落实基本知识的理解

著名数学家华罗庚说过：“数形本是相倚依，焉能分作两边飞。数缺形时少直觉，形缺数时难入微。”数形结合既是一种数学思想，又是一种数学方法。在平时的教学中，有些知识学生会难以理解，恰到好处地使用数形结合的方法进行教学，可以化抽象为形象，促成学生对基本知识的理解。

我们在教学小数的近似数这一内容时，经常会碰到如“1.50和1.5谁更精确”这样的问题，这也是这一内容的难点。为了让学生更好地理解，完全可以借助数形结合的数学思想，避免生硬的说教，直观呈现，发展学生思维。

• 演示操作，落实基本技能的掌握

演示是指教师在课堂教学中，向学生展示各种直观的教具、运用电教媒体或做某项实验等，使学生通过观察获得直观的、生动的感性认识，从而促进理性的感悟。教师的演示操作不能简单地定义为：老师示范，学生模仿。教师在教学中配合适当的演示，可以让学生从教师的演示过程中去归纳、概括所学的知识，从而形成一定的技能技巧。

比如，在教学《认识平行线》这一课时，在认识了平行线之后，要学习平行线的画法，在让学生尝试了各种方法之后，教师要将平行线的画法进行演示。教师在演示的过程中还要纠正三角尺的各种错误摆法，务求正确、规范，并要求学生注意观察，将老师的每一个动作用一个字归纳出来。这样，教師的演示是直观的，学生的归纳是抽象的。通过这样的演示，最后归纳出平行线的画法：一摆，二靠，三移，四画，学生很好地掌握了画平行线的技能。

• 适时渗透，落实基本思想的形成

美国教育心理家布鲁纳指出：掌握基本的数学思想，能使数学更易于理解，更利于记忆，领会基本数学思想和方法是通向迁移大道的“光明之路”。 教师在日常教学中适时渗透数学思想方法，对进一步深化数学课堂教学极其重要，这样可避免“题海战”，减轻学生学习负担，提高学生数学能力，更是培养学生创新意识的必要条件。在课堂教学中渗透数学思想又要尽量做到直观，这样可以避免晦涩难懂。在小学数学教学中，特别是在概念教学时，由于小学生的年龄小、逻辑思维能力差，加上数学概念大都比较抽象，所以在概念教学时，要多借助直观具体、明确好懂的数学表达形式，帮助学生理解，形成正确的概念。集合图因其具有形象性、准确性、简明的特点，在小学数学概念教学中经常运用。

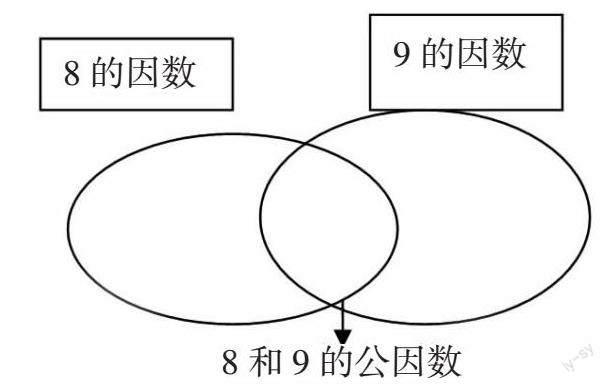
比如，在教学“互质数”的概念时，老师先叫学生用已学过的公因数的知识填下图，接着再引导学生观察8和9的公因数情况，引出：公因数只有1的两个数叫做互质数。集合图在这里清楚地表示出“公因数只有1”这个特征，从而帮助学生准确建立互质数的概念。

除了集合思想，小学数学教材中渗透的数学思想还有：数形结合、对应、分类、函数、极限、化归、归纳、符号化、数学建模、统计、假设、代换、比较、可逆等思想方法。数学思想的形成有一个循序渐进的过程。在课堂探究过程中，教师要根据不同的知识点，适时渗透，直观形象，让学生在探究活动中领悟不同的数学思想方法。

• 实践活动，落实基本活动经验生长

课标指出“数学基本活动经验”是培养学生“创新能力”基石。著名教育家陶行知关于人如何获得知识曾做过一个形象的比喻：“我们要有自己的经验做根，以这经验所发生的知识做枝，然后别人的知识才能接得上去，别人的知识方才成为我们知识的一个有机组成部分。”可见，基本活动经验是学生数学学习的必要前提，是其获得数学直觉的源泉。数学学习离不开活动，学生数学经验的生长是通过参与数学活动实现的。

在教学“长方体和正方体的认识”这一课时，首先要认识长方体和正方体的特征。课堂上，老师让学生动手切萝卜，第一刀切下去，学生感觉面平平的，在切之前萝卜的面是凹凸不平的，让学生体会到生活中的面和数学中的面是不同的；第二刀切下去，多了一个面，两个面相交形成了棱，又让学生认识到立体图形的棱不同于平面图形的边；第三刀切下去，又多了一个角。通过教师的引导，面、棱、角被创造出来，学生获得了具有数学意义的活动经验。接着，老师让学生用学具袋中的小棒搭长方体，有别于以往教学根据教具数长方体棱的条数，使内隐的知识显性化，在学生搭的过程中，学生触及到概念的本质：长方体有12条棱，相对的4条棱的长度相等。然后，教师又出示了长方体连接于同一个顶点的三条棱，让学生想象出六个面是怎样的长方形。随着数学经验的积累，他可以不依附于具体的情境，在头脑中进行合理地推理。学生由棱想到了面，又由面想到了棱，就这样，长方体的特征在学生的头脑中清晰地建立起来。最后，教师出示了几组日常生活中的物体的长宽高，请学生猜一猜是什么东西，说说为什么。能猜中并能说清理由说明学生相关的知识经验已经形成，正如朱德全教授所指出的：“应用意识的生成便是知识经验形成的标志。”

学生的生活经验是丰富的，我们在教学中要尽量结合教材，有利于学生主动进行观察、操作、猜测、推理与交流，让学生经历将生活问题抽象成数学模型。这些都是活动促使经验得以生长。

“双基”变“四基”，对数学教师提出了更高的要求，课堂教学中借助直观教学，以适应儿童的心理特点，促进儿童的健康成长，使人人获得良好的数学素养，不同的人在数学上得到不同的发展。