目标海域中航行船舶横摇谱密度值的预报策略

朱倩云，梁玉珂，沈林维

（浙江大学海洋学院，浙江舟山 316021）

0 引 言

对实际海浪中的船舶耐波性进行分析，需要对不同环境因素下的船舶非线性横摇运动响应进行计算。目前，虽然模型试验在确定船舶横摇方面依旧处于核心地位，但随着数值模拟技术的发展及有利的发展前景，需要更多的数值模拟结果来建立对该问题的一般方法[1-2]。为了更好地探索船舶的横摇运动，本文基于CFD 软件Star-CCM+，利用波浪激励船舶横摇的方式来模拟船舶横摇运动，并计算不同浪向、航速下，遭遇频率大于固有频率的频段中船舶横摇幅值响应算子。

实际海洋环境中的波浪为不规则波，目前尚不能从理论上直接得到海浪频谱。包括Star-CCM+在内的CFD 计算软件,对不规则波的模拟仍是基于传统的海浪谱展式，难以反映海浪情况，因此，探索海浪谱密度的估算方法成为必要。P-M 谱是描述充分发展海洋的典型波谱[3]，本文基于P-M 谱的自相关函数解析式展开研究，以期根据目标海域实测数据修正海浪谱展式，为探索海浪时历信号的自相关函数与海洋环境参数间的关系打下基础。

1 研究流程及船舶模型

本文一方面基于CFD 方法建立数值模型，分析波浪、航速及其耦合对船舶横摇运动的影响，计算得到船舶横摇幅值响应算子；另一方面基于成熟海浪谱展式，推导得到海浪自相关函数表达式，结合目标海域时历数据对其进行修正，反推目标海域海浪谱；最后，结合上面两部分内容对船舶的横摇谱密度进行预报。具体流程如图1所示。

本文选取标模DTMB 5512 作为研究对象，模型与实船的缩尺比为1:46.6，实船与模型的主尺度如表1所示。

采用船体坐标系分析船舶运动姿态，设船舶重心为原点（O），原点指向船艏为x轴正方向，原点指向右舷为y轴正方向，原点指向船底为z轴正方向。

船舶在海上航行时，受到各种作用力和力矩。基于牛顿第二定律建立横摇运动方程式[4]：

式中，Ixx+A44为横摇质量惯性矩系数和附加质量惯性矩系数，N44=B44+B44v为线性阻尼力矩系数和非线性粘性阻尼力矩系数之和，S44为复原力矩系数，ME4(t)为横摇激励力矩。

表1 DTMB 5512船模与实船主尺度Tab.1 Principal dimensions of ship model DTMB 5512

2 横摇幅值响应算子计算

2.1 数值模型

在参考文献[14]的基础上，利用Star-CCM+对船舶运动进行数值模拟。下面对船舶横摇数值模拟的物理建模过程进行说明。

（1）物理模型

求解基于雷诺平均的连续方程和动量守恒方程[5]：

式中，u=(u,v,w)代表时均速度场，u、v、w是速度矢量在x、y和z方向的分量，ρ是模拟中水或空气的密度，p*代表时均压力，f代表质量力，μν为动力粘度，τRe为雷诺应力。利用SSTk-ω湍流模型来计算获得雷诺应力。

船舶运动过程中，采用二阶VOF（volume of fluid）方法来捕捉自由液面。同时，采用二阶迎风格式离散对流项，并选取隐式方法，利用分离流模型求解非耦合条件下的控制方程。

（2）计算域

根据ITTC 船舶CFD 应用指南[6]，建立一个长方体计算域。计算域包括流入面和流出面，流入面施加一个已知的速度场；流出面设置为压力出口边界，并以阻尼消波方式抑制回流；将两侧、顶部和底部边界设为速度入口来避免壁面和流动间产生速度梯度。上述边界条件设置能将所有横向边界上的流动都指向出口边界，保证边界上的流动反射速率最小。分别将流入面、流出面、两侧边界、顶部边界和底部边界设置在离船重心2倍船长处、4倍船长处、2.5倍船长处、1.5倍船长处和2.5倍船长处。

（3）网格划分

为捕捉船舶大幅横摇运动，采用重叠网格法，包括船体域和背景域网格划分。针对船型特征和横摇研究特点，首先对船体控制区域进行整体网格加密，再对球鼻艏、舭龙骨等区域进行局部加密；针对规则波问题，自由液面应保证每个波长内至少包含40 个单元格、每个波高范围包含20 个单元格[7]，为准确捕捉液面波动，本文将自由液面网格加密区的垂向距离扩充至两倍波高。共计网格608.11 万个（背景网格165.55万个，重叠区域网格442.56万个）。

（4）时间步长

本文考虑ITTC 推荐的时间步长和库朗数来确定时间步长。船模的横摇固有周期为1.54 s，根据ITTC推荐得时间步长Δt＜0.0154 s；为保持数值稳定性，要求满足网格单元的库朗数CFL小于1，自由表面的库朗数小于0.5[1]，波浪中的横摇计算以自由表面最小网格尺寸来确定时间步长，即Δt＜0.003 125 s。本文取时间步长为0.003 s。

（5）数值验证

除文献[13]提供的数值验证之外，本文对初始强迫横摇角为10°、傅汝德数Fr=0.41的船模衰减横摇进行了仿真，以进一步验证数值模型。模拟结果与试验结果对比如图2 所示。

船舶在静水中衰减，半个周期内横摇幅值由ϕi变为ϕi+1，由于横摇在到达峰值时横摇角速度皆为零，根据能量守恒定律可知势能变换等于阻尼耗散能量。

船舶势能变换为

图2 横摇衰减曲线对比图Fig.2 Comparison of roll attenuation curves obtained by test and simulation

式中，D为船舶重量，-- --GM为初稳性高

将阻尼力矩展开为三次项形式，有

则阻尼做功，即消耗的能量为

用弧度制绘制消灭曲线并进行三次多项式拟合：

得到系数a、b、c。

将式（7）代入式（4），根据ΔE=W可得

可求得等效线性阻尼系数：

拟合曲线峰值得到的阻尼系数如表2 所示。CFD 模拟结果中，一次和二次阻尼系数与试验结果较吻合，三次阻尼系数相差较多；横摇幅值不大时，三次阻尼系数对阻尼力矩影响较小。稳态周期横摇时，线性阻尼系数Nϕ1和平方阻尼系数Nϕ2可视为常数；但大幅横摇时，存在船舶舭龙骨出水的情况，此时Nϕ1、Nϕ2并非常数，Bassler[8]将其视为分段函数，传统的利用横摇衰减技术得到的横摇衰减曲线计算等效线性阻尼的方法并不适用。

表2 阻尼系数对比Tab.2 Comparison of damping coefficients obtained by test and simulation

2.2 横摇模拟

本节基于CFD 方法考虑不同自由度、航速、遭遇频率、浪向等对横摇运动特性的影响。为保持结果的一致性，船舶初始横摇角设置为0°，受波浪激励发生横摇运动。

2.2.1 模拟工况

如表3 所示，选取12 种工况研究波浪频率、浪向和航速对横摇运动特性的影响，横摇激励采用了一阶线性规则波激励，波高为0.06 m，监测了Fr=0.246（中等航速）和Fr=0.41（高航速）两种航速状态，以及中等航速下270°和225°浪向角（浪向角为船舶前进方向与波浪传播方向的夹角，且以波浪传播方向顺时针度量，如图3所示）。在模型尺度下，选取谐摇区激励频率作为研究对象，研究遭遇频率大于船模固有频率的频段，遭遇频率计算式如下：

表3 横摇模拟工况Tab.3 Simulation of rolling conditions

式中，ω为波浪频率，U为船速，βwave为浪向角。

2.2.2 结果分析

为了便于分析，一致截取物理模拟时间前20 s进行对比。图4 显示了不同航速、波浪频率下船舶横摇时历变化曲线。可以发现，经过几个周期后，横摇运动趋于稳定。

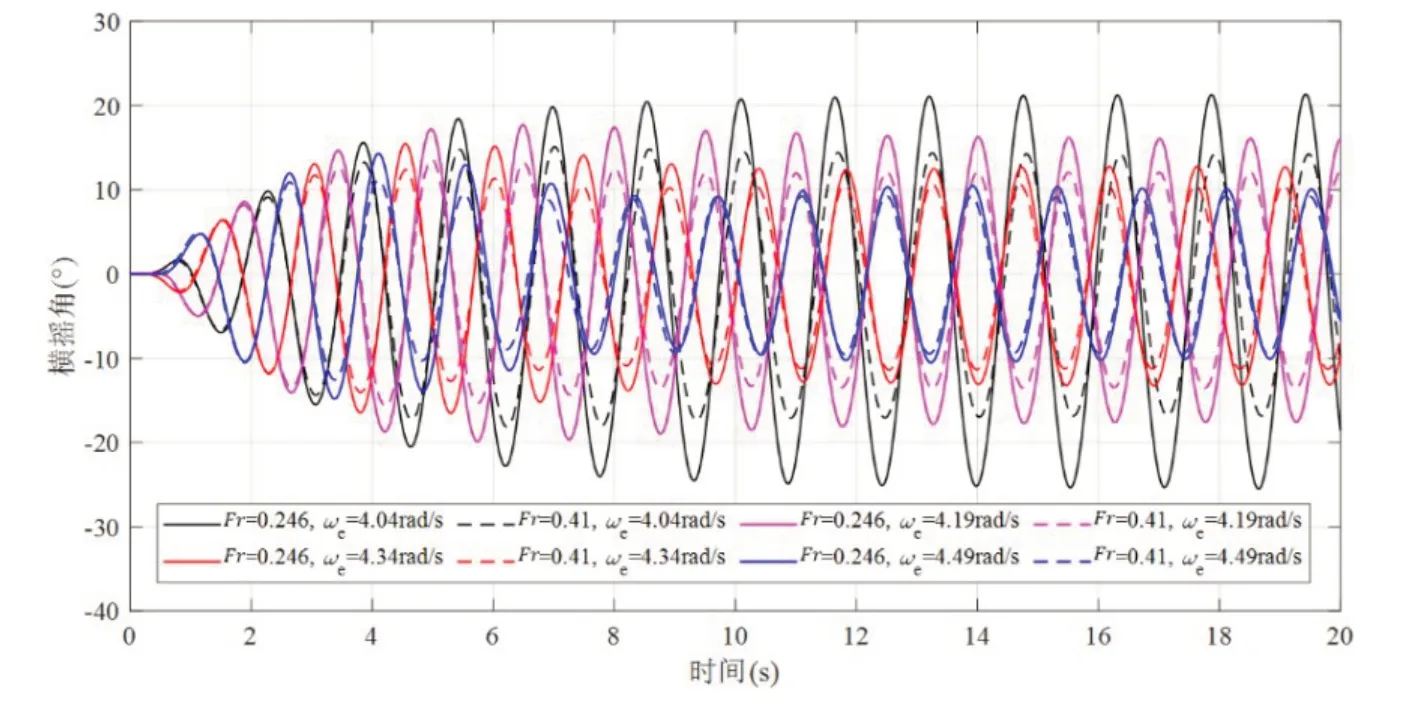
图4 不同激励频率、航速下船舶横摇时历对比图（横浪）Fig.4 Comparison of ship roll histories at different excitation frequencies and speeds (transverse wave)

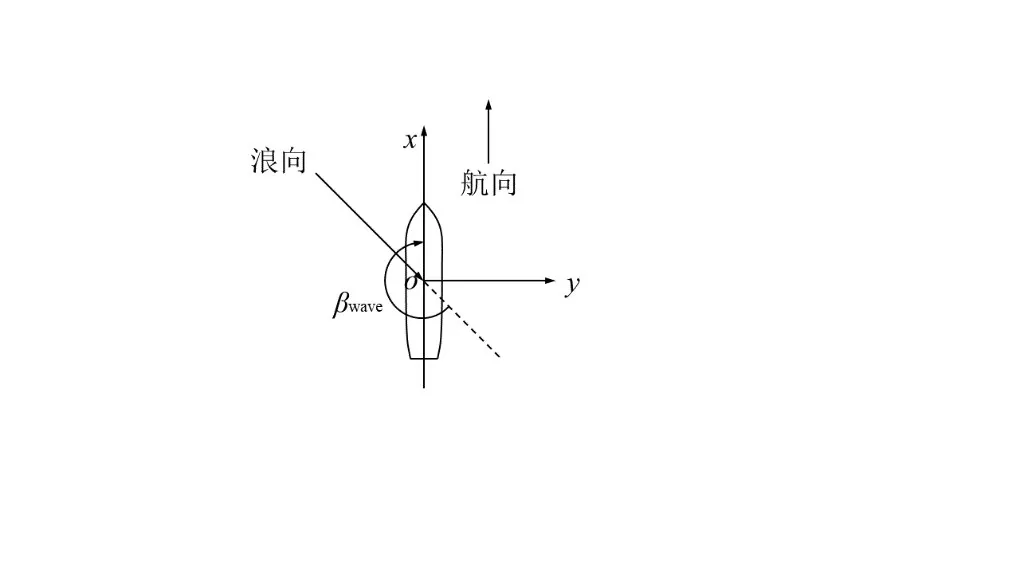
图3 浪向示意图Fig.3 Schematic of wave direction

（1）频率

不同航速下横摇幅值随频率的变化情况见图5。可以发现在不同频率的横浪条件下，船模在频率为4.04 rad/s 下会产生较大的横摇运动特性幅值，此时波浪频率最接近模型的固有频率；随着波浪频率远离固有频率，稳定周期内横摇幅值越来越小。

（2）航速

本文根据简谐激励技术估算不同航速横摇阻尼[9]。如图6 所示的横浪工况中，在4.19～4.49 rad/s 频段内，航速较高的情况下横摇阻尼更大；高航速条件下，本文研究频段与其固有频率相差较大，同一频率下横摇幅值较中等航速中横摇幅值小；中等航速工况中，横摇阻尼变化也更快；Fr=0.246 时，4.04 rad/s 的遭遇频率已接近船固有频率，产生较大横摇角，导致船舶舭龙骨出水，再入水时受到自由表面冲击，同时伴有气泡入水，横摇阻尼进一步增加。

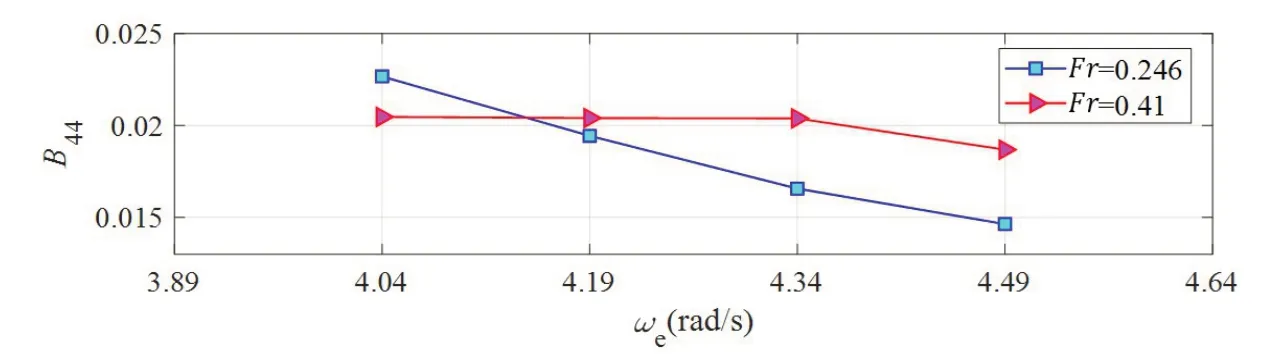
图6 无因次阻尼系数B44Fig.6 Roll damping coefficients B44

图5 不同航速下船舶最大横摇角随激励频率变化Fig.5 Variation of maximum roll angle with wave frequency at different speeds

（3）浪向

本文以225°浪向角的艏斜浪下、Fr=0.246工况为例，对与横浪工况中相同遭遇频率的船舶横摇响应值进行求解分析。

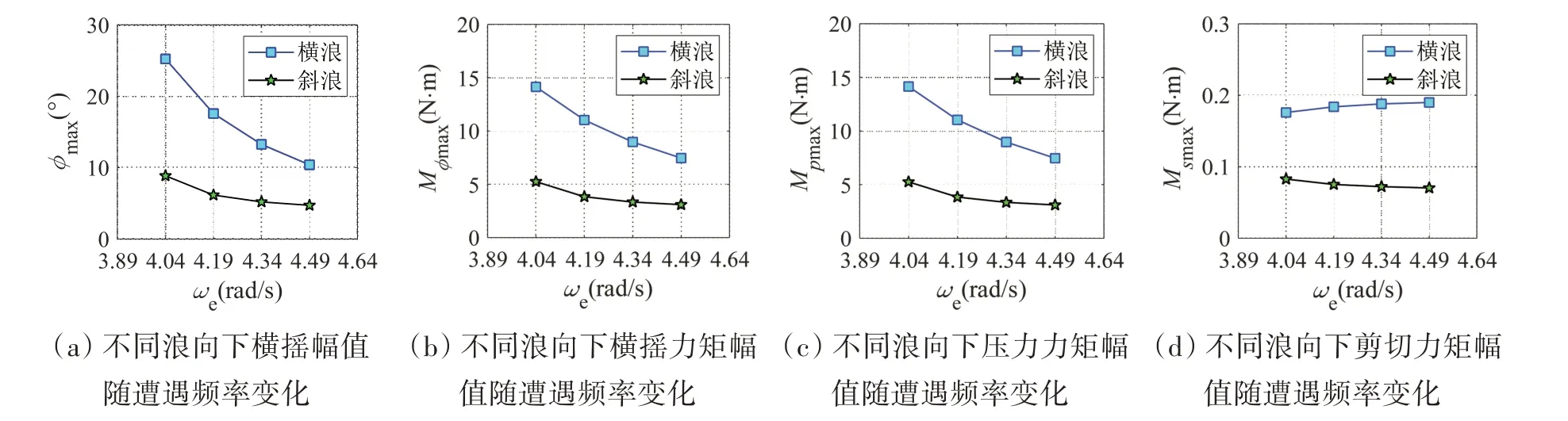
图7 不同浪向下横摇特性随遭遇频率变化Fig.7 Variation of rolling characteristics in different wave direction conditions with the encountered frequency

如图7（a）所示，在同样遭遇频率下，艏斜浪中横摇幅值较横浪情况下大幅减小。稳定横摇时，不同浪向下船舶所受总力矩、压力力矩和剪切力力矩幅值对比分别如图7（b）、图7（c）和图7（d）所示。同一遭遇频率下，斜浪中船体所受横摇压力力矩较横浪中小（见图7（c））；而斜浪中由于航速和波浪传播速度的叠加，自由表面水相对船体流速增大，因此横摇中船体所受摩擦力矩减小（如图7（d）所示）。

2.3 结果统计

横摇频率响应函数（RAO）可以表示为

式中，ζA为波幅。

模型与实船存在以下关系：

图8 横摇RAO2Fig.8 Roll-RAO2

式中，下标‘s’和‘m’分别表示实船和模型。从而可得实船的RAO如下：

统计12种工况下横摇响应幅值计算结果，根据船模遭遇波浪频率对应的实船遭遇波浪频率为0.6 rad/s、0.62 rad/s、0.64 rad/s和0.66 rad/s。绘制实船横摇RAO2曲线如图8所示。

3 海浪谱

通过对P-M 波谱对应的自相关函数的解析式修正得到目标海域海浪谱展式，有利于对特定海域的波浪进行有效表达，可为目标海域中的船舶横摇谱密度预报提供新思路。

3.1 P-M谱自相关函数

数学建模技术的发展为海浪自相关函数的研究提供了便利，Yang 等[10]借助Maple 软件推导出PM波谱对应的海浪自相关函数表达式为

式中：α=8.1×10-3；β=0.74；g为重力加速度，单位m/s2；V为海面上19.5 m高度处的风速，单位m/s；S(ω)的单位为m2·s；Meijer-G函数是一个可以表示大部分特殊函数的通用函数，其表达式[11]定义如下：

式中，0≤m≤q，0≤n≤p，且对于任意j和k，Γ(bj-s)的极点不得与Γ(1 -ak+s)的极点重合（其中，j=1,…,m;k=1,…,n）。

3.2 目标海域自相关函数

如图9所示，选取某实验室不规则波仿真程序模拟得到的有义波高为3 m、跨零周期为8.16 s的波浪时历，时间步长为0.04 s，数据长度为20 000。

海浪谱估计时，常将海浪视为平稳随机过程，即海浪信号ηt的期望μη和标准差σ不随时间t变化，其自相关函数可表示为时间延迟τ的函数：

利用Matlab求得其自相关函数，如图10中红色实线所示。图10中蓝色虚线为相应风速下由P-M谱自相关函数表达式所绘制的曲线。

图9 海浪时历曲线Fig.9 Time history of wave height

图10 P-M波谱对应自相关函数与实际海浪自相关函数对比Fig.10 Comparison of autocorrelation function obtained from P-M spectrum with actual wave autocorrelation function

两条曲线变换趋势基本一致，可以通过设置修正系数来修正由P-M波谱得到的自相关函数。

（1）两参数修正

观察由P-M 波谱得到的自相关函数曲线与目标海浪实际相关函数曲线，设置γ1和γ2两个修正系数对P-M波谱得到的自相关函数进行初步修正，修正自相关函数表达式如下：

令γ1=0.708，γ2=2.05，修正后的自相关函数曲线与目标海域实际自相关函数曲线的对比如图11 所示。两参数修正后的自相关函数曲线与目标海域海浪时历得到的自相关函数曲线相对吻合但还有一定差距，拟纳入第三个参数γ3对由P-M波谱得到的自相关函数进行修正。

（2）三参数修正

设置γ1、γ2和γ3三个修正系数对P-M 波谱得到的自相关函数进行进一步修正，修正自相关函数表达式如下：

令γ1=0.595，γ2=1.77，γ3=0.5，三参数修正后的自相关函数曲线与目标海域实际自相关函数曲线对比如图12所示，三参数修正得到的自相关函数曲线与目标海域海浪时历得到的实际自相关函数曲线拟合良好。

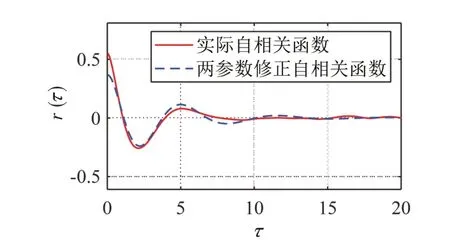
图11 两参数修正自相关函数与实际自相关函数对比Fig.11 Comparison between the autocorrelation function obtained by modifying the two parameters and the actual wave autocorrelation function

3.3 目标海域海浪谱

由维纳-辛钦定理可知，已知目标海域海浪自相关函数，易得海浪谱密度函数。由式（17）推得海浪谱密度函数：

由式（18）推得海浪谱密度函数图像如图13 中的修正波谱曲线。

通过对图9 的海浪时历数据直接进行谱分析来比较验证图13 中的修正波谱。为减小谱分析误差，本文使用周期图谱估计，对数据分块处理[12]，最后将估计得到的海浪谱密度函数进行样条拟合得到图13 中的红色虚线。对比图13中的三参数修正波谱与谱估计拟合曲线，可以发现海浪谱峰值十分接近，且频率分布接近。

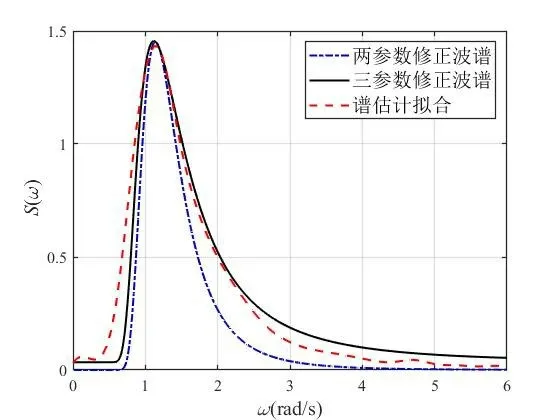
图13 海浪谱Fig.13 Ocean wave spectrum

4 横摇谱密度

对于波浪中船舶的横摇运动问题，将船舶视为线性系统，则海浪谱为输入，横摇响应幅值算子RAO为传递函数，横摇谱密度为输出且等于海浪谱和响应幅值算子的乘积，即

结合修正海浪谱，绘制横摇谱密度，如图14所示。

5 结 论

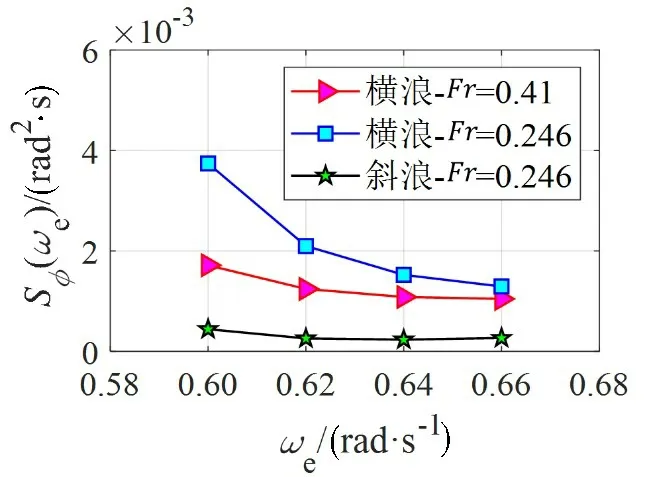
图14 横摇谱估计Fig.14 Roll power spectral density

本文针对DTMB 5512 船模的耐波性问题，着重研究难以独立预报横摇阻尼的情况中船舶的非线性横摇运动表现，探究了各因素对船舶横摇幅值的影响；同时基于P-M波谱公式推导出的海浪自相关函数表达式和海浪数据获取了目标海域海浪谱，进而预报船舶横摇谱密度。结论总结如下：

（1）通过对CFD 仿真结果分析发现，相同频率的横浪激励下，增大航速会增大横摇阻尼，并增大船体两端压差从而抑制横摇，船舶横摇幅值减小；随着遭遇频率远离固有频率，船舶横摇幅值越来越小，受涡旋的产生、舭龙骨出水等因素的影响，呈非线性变化；受波浪与航速的耦合作用影响，相同遭遇频率下，225°浪向角的艏斜浪中船舶的横摇幅值小于横浪中的船舶横摇幅值。

（2）结合目标海域的离散海浪数据对基于P-M 波谱公式推出的海浪自相关函数进行修正获取目标海域海浪谱。研究表明，基于Meijer-G 函数可以对海浪自相关函数进行有效表达，利用海浪自相关函数推导海浪谱有助于解决无法用光滑的海浪谱对其海浪能量分布进行精准表达的问题，可以靶向服务于特定目标海域中航行船舶横摇谱密度的预报。