大型框架式渔业平台水动力分析及其系泊系统设计

俞 俊，程小明，张 凯，倪歆韵，苗玉基，刘小龙

（中国船舶科学研究中心，江苏无锡 214082）

0 引 言

近海区的过度捕捞以及污染排放造成的富营养化，致使多数临海国家的近海渔业资源显著减少。渔业模式正从传统的海洋捕捞为主逐步向捕捞与养殖相结合转变，利用远海渔业养殖技术开发渔业资源，已成为海洋渔业经济发展的方向。渔业养殖平台[1-2]是人工养殖鱼类的新型装备，在海上不可避免会受到来自波浪和海流的共同作用，由此产生对平台主体以及渔网面的复杂组合载荷作用，从而容易使得平台发生倾覆乃至系泊缆失效而失去定位功能。

传统网箱[1-2]通常是柔性的，但柔性和可变形的支撑结构很难承受来自海浪、风和流的巨大载荷。大部分使用的柔性网箱都可以归类为重力式网箱，这些网箱由一个表面环结构作为保持架，一张网悬挂在水柱中，底部悬挂重物以保持网箱的形态。高强度聚乙烯（HDPE）网箱是最广泛使用的重力式网箱[3]，被认为是波浪柔顺的，即它随波浪而弯曲，而不是保持刚性。

近年来，由于不断向外海拓展[4]，网箱设计出现了以下发展趋势：使用更刚性和坚固的框架，以承受强风浪作用。大型框架式渔业平台的特点是利用立柱及横斜撑将网衣支成固定的形状，使其有效养殖容积基本保持不变，即使在强风浪流情况下也不会造成容积损失。到目前为止，越来越多的学者对波浪和海流下的半潜式近海渔场动力响应进行研究，集中在水动力特性、波浪激励和系泊载荷方面，极大地促进了对环境载荷和大型框架网箱平台之间相互作用的力学理解。Dou[5]研究了主尺度为110 m 的刚性半潜式渔场Ocean Farm 1，在GeniE 中建立了Ocean Farm 1 的有限元模型，在hydrod 中完成了水动力计算，将水动力结果输入SIMA 进行时域响应计算；Zhao 等[6]通过一系列物理模型试验，研究了刚性半潜式渔场Ocean Farm 1的水动力性能，采用的主尺度直径为120 m，系泊系统由四条360 m长的系泊缆组成，水深为120 m，针对三个不同吃水，测量了渔场波浪作用下的系缆张力和运动响应；Shi[7]参照近海养鱼场Ocean Farm 1设计了刚性框架式渔业平台，结合我国的海洋条件，采用WADAM、WASIM、SIMO 等数值模拟程序分析了其动力响应；Jin 等[8]在SIMA 环境中使用WAMIT、SIMO 和RIFLEX建立了带系泊系统的Ocean Farm 1数值模型，并进行了时域模拟；Palczynski[9]在波浪水池中完成了矩形刚性平台和中央立柱式Sea Station平台的缩比模型测试，确定了两个不同的养殖平台模型的运动和载荷；Yua 等[10-11]设计了一型底部有七个方形浮筒的刚性半潜式养殖平台，分析了不同条件下前后位置系泊张力的变化趋势和波动范围，探讨了瞬时幅值峰值出现的原因。

不同于一般的浮式结构物，渔业平台最重要的是保证养殖鱼类的健康。离岸网箱系统需要能够承受连续的海浪、洋流和风暴，理论上可以设计出永不损坏的系泊系统，但是养殖的鱼类可能先于系泊系统而失效，网衣也可能先于系泊系统出现网破鱼逃的现象，因此渔业平台的系统刚度不能过大。

本文对直径110 m 的大型框架式渔业平台及系泊系统进行水动力计算分析和评估。一方面针对莫里森公式在大入射角下基于横流原理的阻力模型不合理现象，提出基于三个方向的等效水动力系数来模拟渔网遮蔽效应的大型渔业平台复杂水动力分析方法，建立模拟大型框架式渔业平台水动力特性的工程评估模型；另一方面设计具有不同弹性特性的系泊材料组合，能够同时减少网箱受力和减小系泊恢复力的系泊布局，通过时域评估分析验证方案的可行性与经济性。

1 物理模型

1.1 大型框架式渔业平台参数

渔业平台如图1所示，俯视呈正六边形，外接圆直径为110 m，主体框架由不同规格的杆件和浮筒构成，六个顶点和平台中心处的圆柱直径为3.6 m，顶点连线中心处的圆柱直径为2.8 m，此外还有十二根直径为1 m的斜撑，详细参数见表1。平台底部有两个长度为65 m、底面直径为9.3 m的圆柱形大浮筒提供主要的浮力，两个浮筒的浮力共计8830 t，水线面处为直立或者倾斜的圆柱杆，总面积较小，共计120 m2，由此可见整个平台的垂荡、横摇、纵摇的自然周期将大于常规的海洋平台。大型框架式渔业平台布放在水深为63 m 的较浅海域，浅水效应使平台所受波浪特别是长波的影响较大，作业工况时网箱内有23万方的水体养鱼。

图1 大型框架式渔业平台主体框架Fig.1 Main frame of huge-framed offshore aquaculture platforms

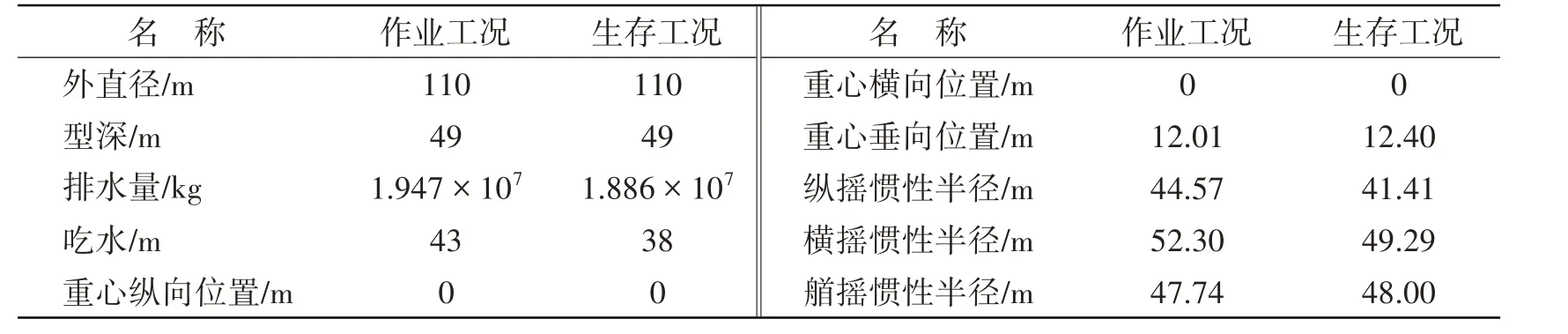
表1 大型框架式渔业平台主尺度参数Tab.1 Main parameters of huge-framed offshore aquaculture platforms

大型框架式渔业平台外围覆盖着合成纤维材料制成的渔网，网线中含有钢丝，渔网原型参数见表2。

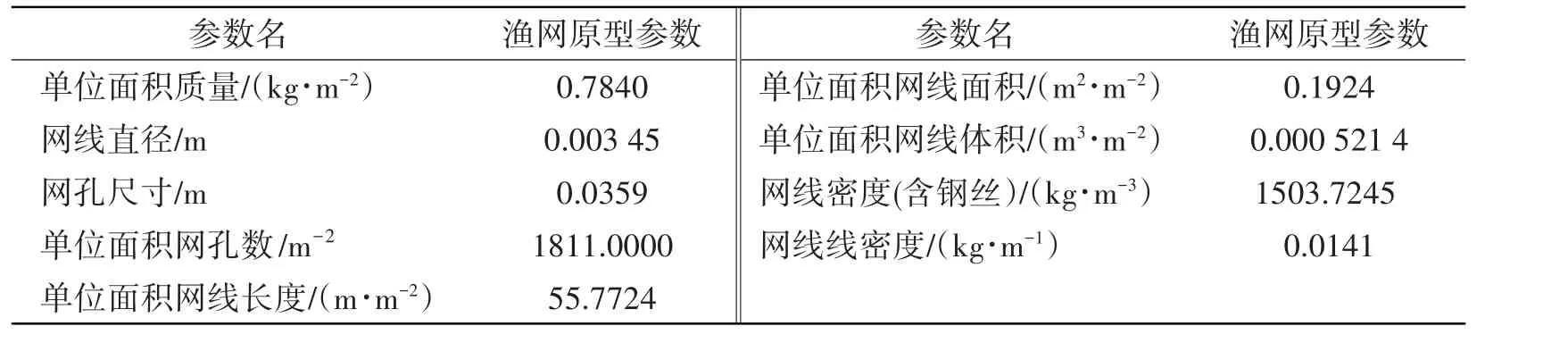
表2 大型框架式渔业平台的渔网参数Tab.2 Net parameters of huge-framed offshore aquaculture platforms

1.2 海洋环境

大型框架式渔业平台设计有作业工况和自存工况，波浪采用JONSWAP 波谱描述，详细海洋环境参数见表3。

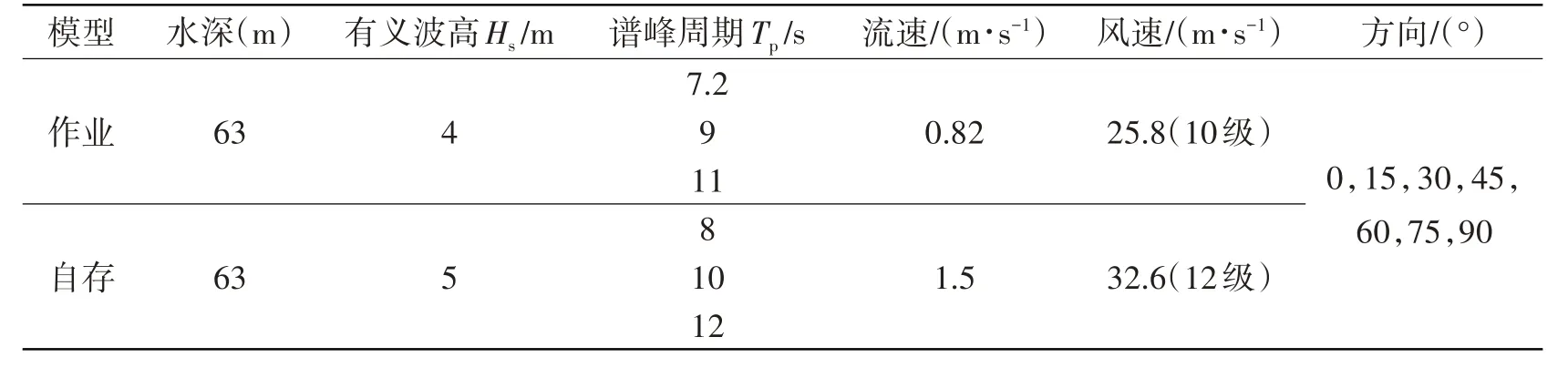
表3 大型框架式渔业平台海洋环境条件Tab.3 Designed ocean environmental of aquaculture platforms

2 水动力模型建立及计算方法

2.1 计算理论

采用三维线性势流理论计算大型框架式渔业平台的水动力载荷与响应，将流场中总的速度势Φ分解为入射势ΦI、绕射势ΦD和辐射势ΦR。假定浮式结构物在平衡位置周围作微幅的简谐振荡，则速度势可分解成空间速度势和时间因子的乘积，这样便可以转化为求解定常运动问题。大型框架式渔业平台主体结构均由细长杆形部件构成，细长杆与波长相比尺度较小，故可以采用莫里森方程计算其波浪力。大型框架式渔业平台大部分形式的结构可用圆形截面Morison单元模拟，由于杆单元会因水流和波浪的存在而移动，因此分别利用杆单元和流体速度之间的相对加速度和速度来计算惯性和阻力载荷，本文采用基于三维势流理论的AQWA 软件进行数值分析。对非圆形截面的杆件采用截面等价后的等体积圆形截面Morison单元替代。

Morison单元单位长度垂直于杆件方向的水动力[12-13]为

式中，D为杆件的特征直径，uf为垂直杆件方向的流体质点速度，us为垂直杆件方向结构自身的运动速度，A为杆件截面面积，ρ为流体的密度，Cm为惯性力系数，Cd为阻力系数。

大型框架式渔业平台四周及底部悬挂的渔网由合成纤维缆绳编织而成，穿插挂于钢丝绳上，钢丝绳均布固定在主体框架的杆件上并施加一定的预张力，这使得渔网的变形实际很有限。对大型框架网箱平台所受到的粘性力，尤其是网衣所受到的粘性力，目前还没有发展出统一的数值模型。对于这个问题，专家学者们进行了大量的分析研究。2003年Lader等[14]建立了三维网结构在波浪和水流作用下的水动力学模型，验证了圆柱形网下该模型的有效性；2012 年Kristiansen 等[15]假设网被分成许多平面的网面板，提出了网的粘性水动力载荷屏模型，可以应用于任意几何形状的网，不过所研究的平台底部没有加网衣；2012年Chen等[16]基于刚体运动学理论和集中质量法，建立了波浪作用下两网箱的网格系泊系统数值模型；2013 年Klebert 等[17]认为养殖网箱内外流体动力受网箱模型尺度的影响；2014 年Cifuentes 等[18]研究了带系泊索、浮标、喂料船和网箱的近海水产养殖系统在波浪和水流作用下的动力响应；2014 年Fredriksson 等[19]采用有限元模型对网箱系统进行了模拟；2015 年Kristiansen 等[20]对一个直径37.5 m的渔业平台设计了八根缆绳的系泊系统，在此基础上进行了数值分析和模型试验研究，然而，作者研究中也假设底部没有网；2016年Chen等[21]提出了一种基于莫里森模型荷载转换的计算多孔阻力系数的新方法，并通过平面网板和圆形网箱的稳流，以及波与平面网板的相互作用来检验数值模型的性能；2017年Chen等[22]基于多孔介质模型和集中质量结构模型之间的耦合，建立了一个水流-结构相互作用分析的网箱数值模型；2018年Gansel等[23]通过峡湾内实尺度拖曳试验研究了网箱在单纯流作用下的受力及变形，得出了关于不同流速下全尺寸网箱的流速、网变形和阻力相互作用的数据。

综合而言，网对流过的流体的影响[18]是阻碍水的流动，具体表现为网的下游流速减缓，以及水从侧面绕到网的下游。目前，常用的基于经验公式计算粘性力的水动力模型有两种[24]，即莫里森公式[25-26]和屏模型[27]。屏模型的优点在于其粘性力可以灵活地转化为法向力和切向力分量或等价为阻力和升力分量，并且便于通过试验确定系数，其主要的缺点是在水动力分析商业软件中较少将该功能嵌入；莫里森公式的优点在于它的简单性和广泛应用于细长海洋结构的分析，几乎所有相关的分析工具都包括选择这样一个水动力模型的选项，莫里森公式的缺点是大入射角下，基于横流原理的阻力模型存在不合理处，即下游网线受到上游网线的“遮蔽效应”没有得到很好的反映。本文将基于莫里森公式来考虑网衣受到的粘性力，在建模阶段就避免上述弊端，具体分析见下节。

2.2 渔网模型建立

不同于传统重力式网箱，大型框架式渔业平台的网由立柱及横斜撑支成固定的形状且本身加有预张力，因此本文将其处理为刚性。此外，考虑到网状结构的通透性，其采用截面等价的圆形杆件代替。针对莫里森公式在大入射角下阻力模型不合理问题[18-29]，本文将通过三个方向的等效水动力系数来模拟所有来流方向的渔网水动力，并通过后侧水动力系数的折减考虑渔网的部分遮蔽效应，即平行于网面方向的遮蔽效应。模拟时作以下两点假设：（1）网完全刚性；（2）对波浪无耗散作用。通过计算获得单位面积上的等效参数，采用Morison单元模拟波浪力及阻尼，获得的模型参数见表4。由此建立网箱的等效几何模型，如图2和图3所示。该模型增添了垂直于网面的、沿着Z方向的莫里森小杆件，便于模拟实际情况中各个方向的来流来浪。

图2 网箱模型局部示意图Fig.2 Morison model of aquaculture net

图3 网箱结构模型Fig.3 Numerical model of cage structure

渔网所受的阻力为

式中，Cdxw和Cdzw是实际网箱的阻力系数，lx是实际单位面积网衣在X方向的长度，lz是单位面积网衣在Z方向的长度，dw是实际网衣的直径。对于同一片网衣，考虑遮蔽效应，沿着网面的阻力系数Cdxw取值0.6，垂直于网面的阻力系数Cdzw取值1.0[28]。此外，鉴于两片平行网衣的距离达到百米级，因此不考虑不同网衣之间的遮蔽效应。

莫里森单元上的阻力为

式中，Cdxm、Cdzm是莫里森单元中的等效阻力系数，lxm是单位面积莫里森单元在X方向的长度，lzm是单位面积莫里森单元在Z方向的长度，dm是莫里森单元的直径。

根据实际情况与模型中的阻力值相等，求得

再计算等效惯性力系数。实际渔网所受的惯性力为

式中，Caxw、Caxw是网箱的实际惯性力系数，Vdxw是单位面积网衣在X方向的投影体积。对于同一片网衣，考虑遮蔽效应，沿着网面的阻力系数Caxw取值0.5，垂直于网面的阻力系数Cdzw取值1.0[31]，莫里森单元等效渔网所受的惯性力为

式中，Caxm、Cazm是莫里森单元中的等效惯性力系数，Vdxm是单位面积莫里森单元在X方向的投影体积，Vdym是单位面积莫里森单元在Y方向的投影体积，Vdzm是单位面积莫里森单元在Z方向的投影体积。

根据实际情况与模型中的惯性力值相等，求得

2.3 渔业平台整体模型

通过大型框架式渔业平台主体框架水动力模型建立方法以及渔网水动力模型建立方法，完成整个大型框架式渔业平台的水动力模型建立，如图4 所示。模型布置沿X轴呈轴对称，定义X轴正向为平台艏部，Y轴正向指向左舷，Z轴在大型框架式渔业平台中心处指向上方，XY平面上与平台底部重合，YZ平面位于中横剖面处。浪向定义：0°为随浪，180°为顶浪。根据船级社规范[31]以及上一节的等效渔网水动力模型系数，各类杆件的阻力系数Cd及附加质量系数Ca取值如表5所示。

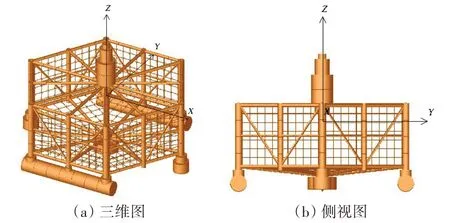
图4 大型框架式渔业平台的水动力模型Fig.4 Hydrodynamic model of aquaculture platform

表5 渔业平台的水动力模型参数Tab.5 Hydrodynamic coefficients of aquaculture platform

3 水动力结果

3.1 静水自由衰减特性

对大型框架式渔业平台进行静水中自由漂浮状态下的衰减模拟，获取平台固有属性运动固有周期。数值计算中分别赋予平台偏离平衡位置6.7 m 的初始垂荡位移、15°的初始横摇和纵摇角度，得到的作业工况自由衰减曲线如图5 所示。曲线上相邻两个峰值或谷值之间的时间间隔即为平台摇荡运动固有周期，通过多个周期数据取平均值，可以得出垂荡自然周期为29.5 s，横摇自然周期为47.6 s，纵摇自然周期为37.5 s。考虑到渔业平台构型以及水线面，横摇和纵摇方向的恢复刚度相接近，所不同的是横摇惯量为5.32×1010kg·m2，纵摇惯量为3.87×1010kg·m2，横摇惯量较大，所以计算得出的横摇自然周期比纵摇自然周期大。同样可得生存工况垂荡自然周期为32 s，横摇自然周期为54.8 s，纵摇自然周期为41 s。

3.2 规则波大型框架式渔业平台运动特性

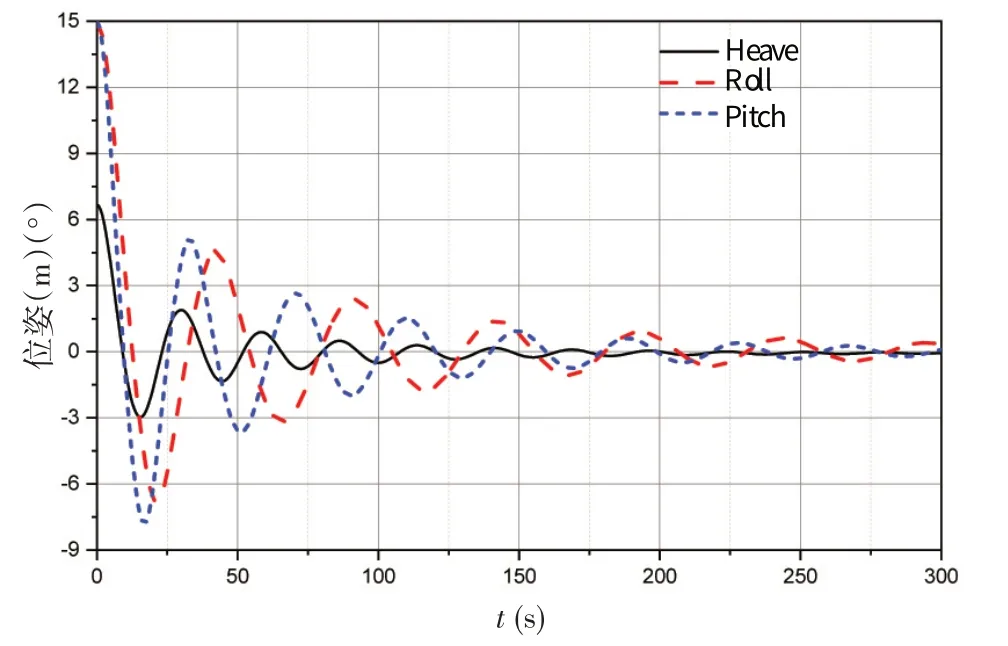
图5 自由衰减曲线Fig.5 Free decay curve

在AQWA-NAUT 模块对大型框架式渔业平台进行时域分析，采用了1 m 波幅的规则波，计算了5个浪向、34 个周期的组合工况，得到了渔业平台垂荡、横摇、纵摇运动幅值响应算子（RAO），图6 展示的是作业工况大型框架式渔业平台RAO 结果。图6（a）表明各个浪向下垂荡结果较为相似，峰值出现在30 s 左右。图6（b）展示了各浪向下的横摇结果曲线，随着浪向从0°逐渐增加至90°，横摇逐渐由0°变大，各浪向下的峰值均在50 s左右。图6（c）展示了各浪向下的纵摇结果曲线，随着浪向从0°逐渐增加至90°，纵摇逐渐减小为0°，各浪向下的峰值均在40 s左右。横摇最大值在50 s出现，为1.1 m，纵摇最大值在40 s出现，为1.6 m，这是由于双浮筒构型横摇转动惯量较大导致的，惯量越大，响应越慢，幅值越小。

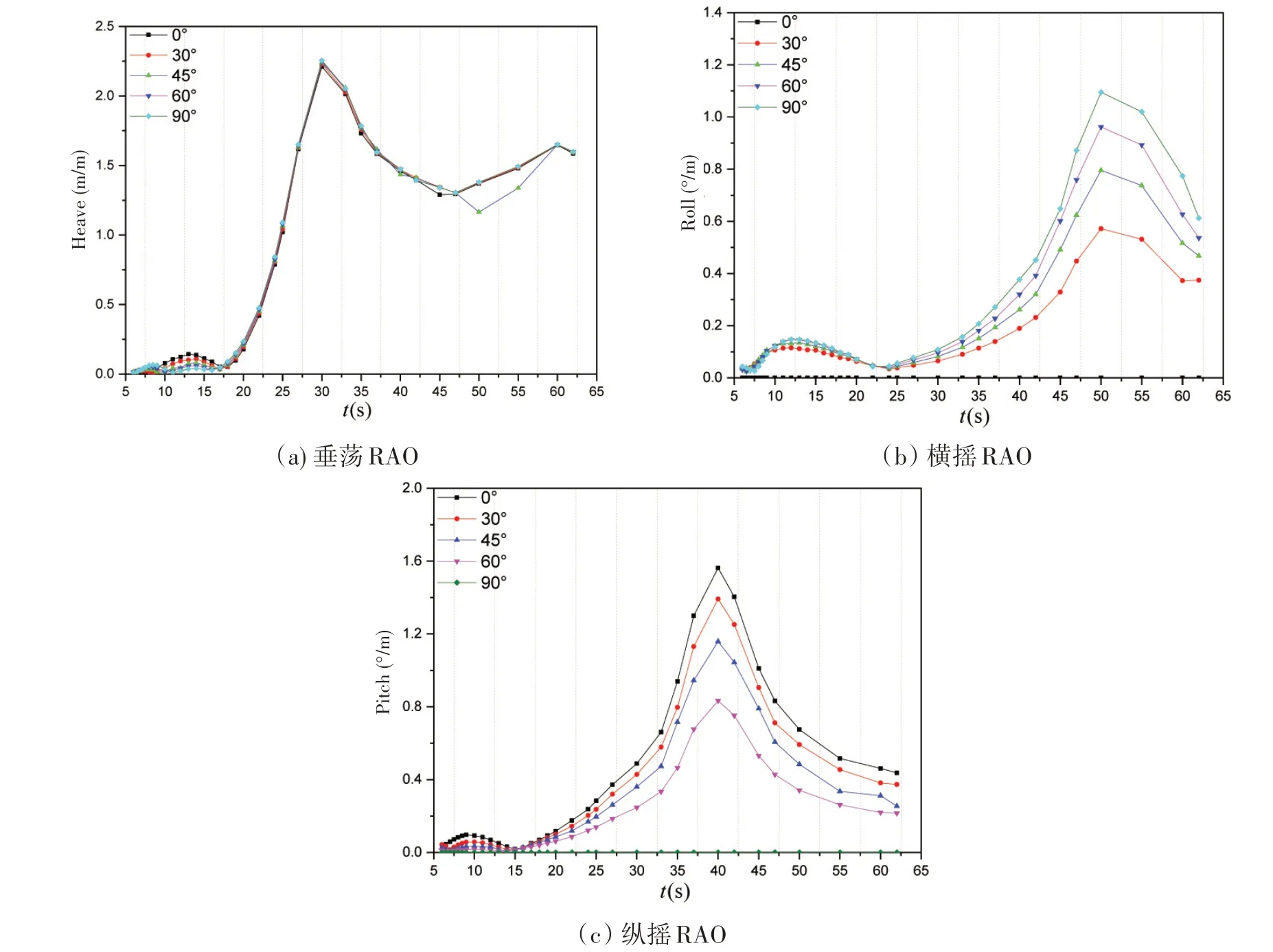
图6 渔业平台运动RAOFig.6 Motion RAO of aquaculture platform

4 系泊系统设计评估

4.1 环境载荷模拟

大型框架式渔业平台上部结构布置养殖设备，有一定的受风面积，且距离平台重心较远，风倾力臂较大。本文大型框架式渔业平台生存工况X方向的迎风面积为621 m2，Y方向的迎风面积为716.9 m2，所受的风载荷风力作用中心距结构重心39.6 m。计算过程中给定与速度无关的风力系数、风力矩系数，使用过程中乘以风速的平方可以得到具体受力情况。X方向风力系数在0°时达到最大，Y方向风力系数在90°时达到最大，随着风向变化，风力及风力矩系数在X、Y轴也相应发生变化，具体参数如图7所示。

随机波浪参数采用短期海况谱型为JONSWAP 进行时域分析，谱峰提升因子为2.0，波流具体参数参照表3，时域计算分析能够模拟渔业平台当前风浪流海洋条件下的运动响应，计入前一时刻对后一时刻的影响尤其是在冲击载荷作用下平台的运动、一阶波浪力等水动力响应演化状态，能更加真实地反映其在各种海况下的运动状态。

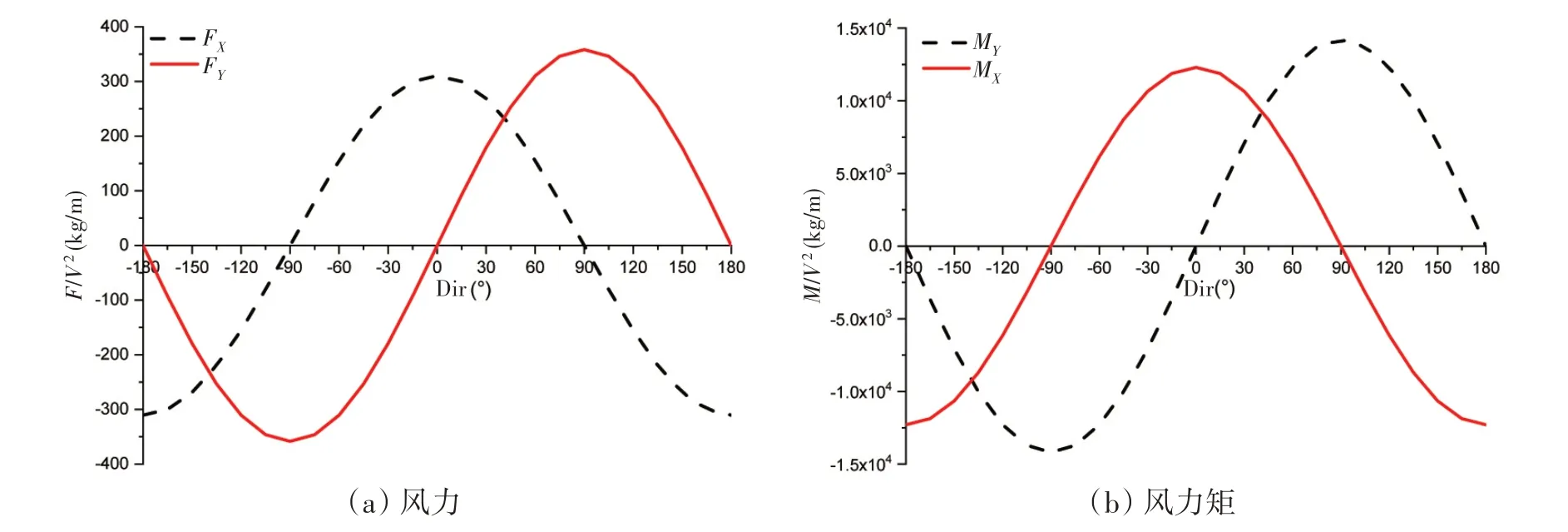
图7 风力系数Fig.7 Wind coefficients

4.2 大型框架式渔业平台系泊系统

大型框架式渔业平台因其特殊构型，无论风浪流从哪个方向而来，迎流迎浪面都较大，所承受的环境力也差不多，此外大型框架式渔业平台布置在水深较浅的63 m 处海域，属于浅水系泊。在以上大型框架式渔业平台水动力分析的基础上，首先考虑分布式系泊系统，这样无论在哪个方向，平台都将被牢牢地约束住，但这也将导致系泊锚链较多，成本较高，且背浪侧大部分锚链处于较松弛状态，浪费资源。因此，本文最终设计了平行式复合系泊系统，组合采用了不同尺寸的锚链和合成纤维缆绳的混合式系泊方案。四组缆绳平行于Y轴，一端分别连接到四根立柱上，另一端连接在海底锚固点，如图8所示。右舷从艉部到艏部缆绳编号分别是1和2，左舷从艉部到艏部缆绳编号分别是3和4。环境条件0°方向表示风、浪、流来自负X轴方向，90°方向表示风、浪、流来自负Y轴方向。表6 为系泊点位置详细坐标。为了使复杂系泊系统满足特定环境的使用需求，需要分析锚链以及合成纤维缆绳的性质和力学表现。通过多次优化迭代后，得到了图9所示的缆绳组成。

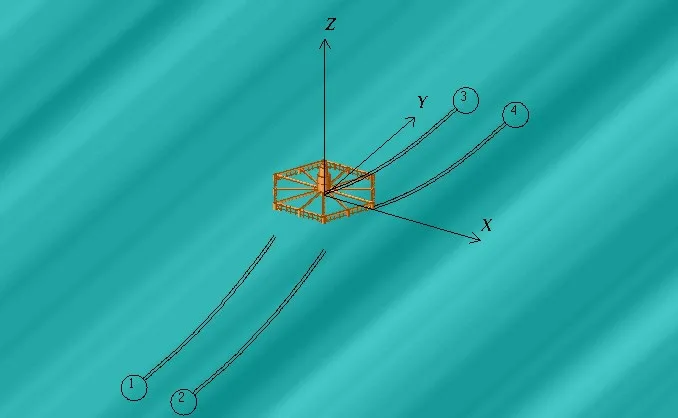
图8 大型框架式渔业平台系泊示意图Fig.8 Model of mooring system of aquaculture platform

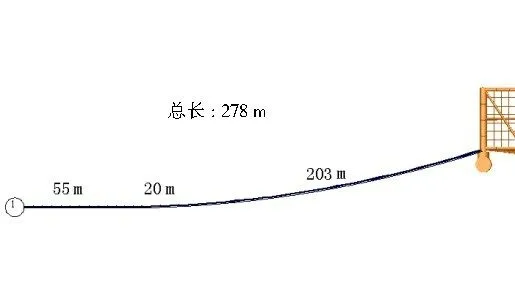
图9 缆绳组成Fig.9 Composition of mooring line

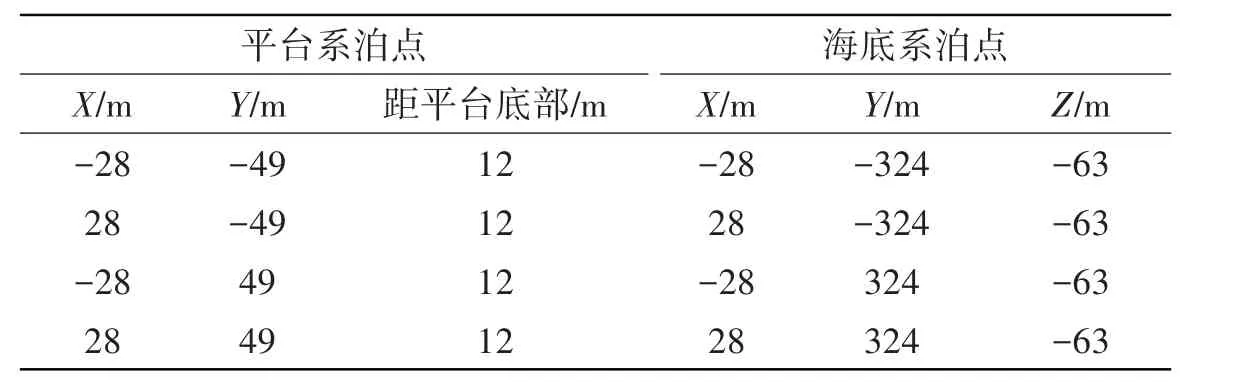
表6 大型框架式渔业平台的系泊点位置Tab.6 Coordinates of mooring points

缆绳的具体参数如表7所示。整个复合系泊系统提供了不同方向下的合适刚度，使得渔业平台在严酷海洋环境下可以在位运行。海底段选择湿重如此大的锚链组合是为了避免对锚固基础产生上拔力。因为浅海系泊中，锚链的悬链线形态不易呈现，因此锚固基础容易出现垂向上拔分力，较重的海底段锚链可以防止此种情况发生。

表7 单根系泊缆绳力学参数Tab.7 Detailed mechanical properties of mooring lines

赋予渔业平台多个浪向下的不同水平面内位移，可以得到单根锚链水平方向的刚度以及整个系泊系统的回复刚度，如图10～11所示。结果表明，无论是观察单根缆绳还是整个系统，它们均在X方向具有较小的刚度且表现出一定的非线性，而在Y方向具有较大的刚度。

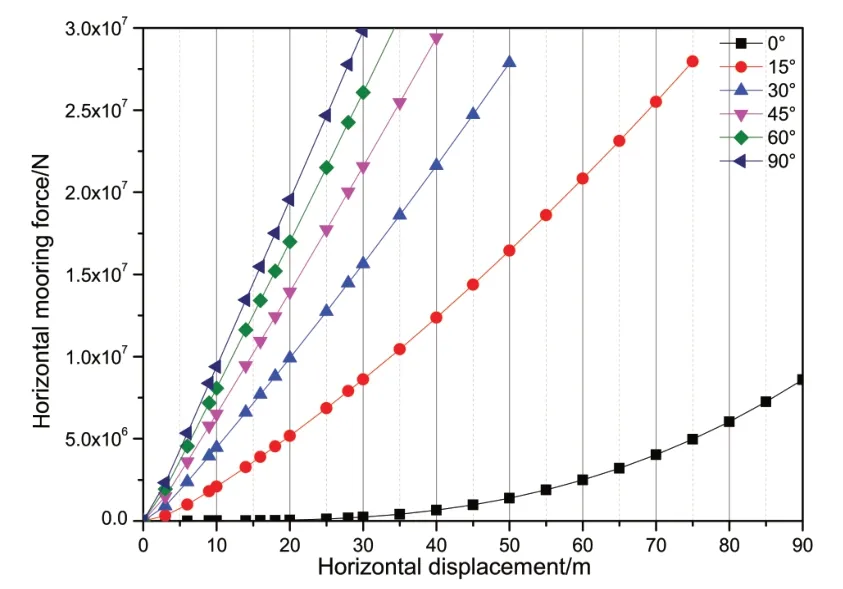
图11 系统回复力Fig.11 Horizontal stiffness curve of mooring system

4.3 系泊系统计算结果

借助软件模块AQWA-DRIFT 进行系泊系统计算分析，得到了大型框架式渔业平台受到的水动力、锚链以及合成纤维缆绳受到的拉力。每个浪向周期下采用10个随机波浪seed，通过3小时时域计算，得到系泊系统锚链张力的Gumbel分布计算结果。选取生存工况的计算结果，如图12～14所示。缆绳最大张力不超过746 t。整个系泊系统安全系数为2.07，大于规范中要求的2.0，满足要求。从张力结果图中可以看出当风浪流来自于0°时，四根缆绳的受力大致相当，为650 t 左右。当风浪流来自于90°时，缆1、2 的受力相当，为500 t 左右，背浪侧的缆3、4 基本不受力。在其余浪向下，缆1 的受力最大，缆2次之，缆3受力最小。缆绳最大张力发生在30°浪向下，此时缆1最大张力达到746 t。

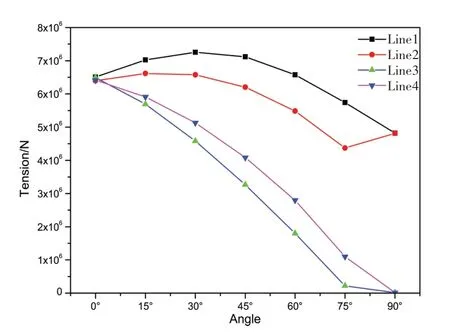
图12 8 s周期系泊张力结果Fig.12 Mooring tension results in 8 s period

图13 10 s周期系泊张力结果Fig.13 Mooring tension results in 10 s period

考虑单缆破断情况下整个系泊系统的安全性，缆绳1 所受的张力较大，对缆1 进行破断分析。首先分析聚酯缆绳破断一股的情形，由于聚酯缆绳采用环绕的方式连接，故此一旦破断，相当于两根聚酯缆绳失效，缆1 的破断力下降一半为7.7×107N，刚度也降低。因为四根系泊缆的刚度差异（刚度由5.225×107N 降为2.624×107N），系泊系统实质上不对称，因此在0°浪向下四根缆绳张力差异较大。所得的系缆力时域结果如图15所示。此时缆2受力最大达到824 t，安全系数为1.87，缆1 受力最大505 t，安全系数为1.52，大于规范中要求的1.46，符合要求。接着分析中间段锚链破断一股的情形，缆1 的破断力下降一半为1.088×107N，刚度由5.225×107N 降为5.199×107N，变化不大。计算结果如图16 所示，此时缆1 最大受力为744 t，安全系数为1.463，符合规范要求。

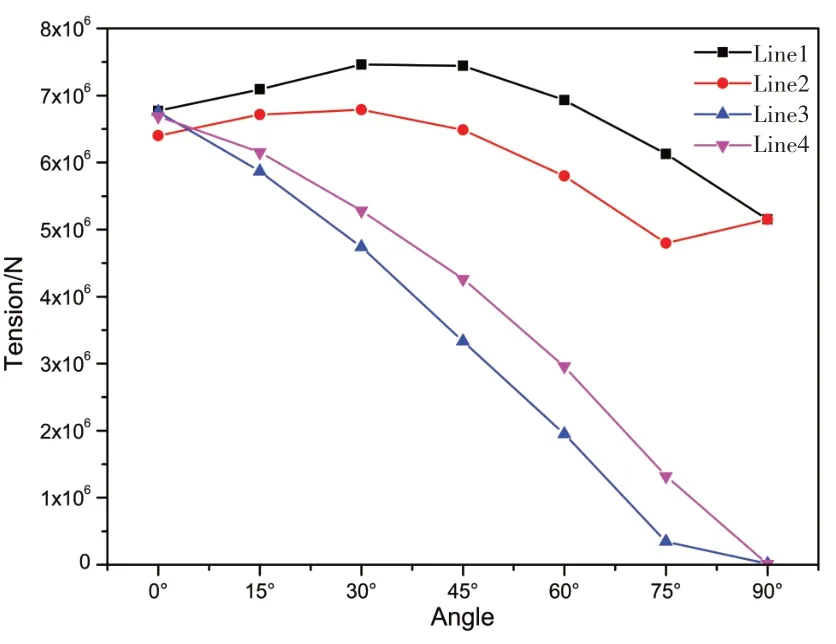
图14 12 s周期系泊张力结果Fig.14 Mooring tension results in 12 s period

图15 单股聚酯破断系泊张力结果Fig.15 Mooring tension results with one strand polyester break

图16 单股锚链破断系泊张力结果Fig.16 Mooring tension results with one strand chain break

4.4 系泊系统造价评估

对整个系泊系统造价进行初步评估，得到的总价大致为833.77 万元，详见表8。整个系泊系统有较低的成本，具有经济适用性，可在实际工程应用中使用。

表8 系泊系统造价Tab.8 Cost of mooring system

5 结 论

本文对直径110 m 的大型框架式渔业平台进行了水动力评估，并进行了系泊系统优化设计；通过平行于网面的遮蔽效应和参数等效，基于三个方向的等效圆形截面Morison 单元，建立了模拟所有来流方向的渔网数值分析模型；结合主体框架数值模型最终建立了渔业平台整体的工程评估水动力模型；通过时域评估分析验证了方案的可行性与经济性。本文的方法能快速计算网箱的水动力，可为设计阶段分析评估渔业平台在位运行时的水动力性能提供有效手段。通过计算分析，获得了以下结论：

（1）大型框架式渔业平台的自然周期较大，主要由两方面的原因引起，一方面是其湿表面较小，另一方面是其大面积的网具有较大的粘滞效应。

（2）渔业平台在位运行时所受到的波浪力较大，尤其生存工况时有义波高达到5.0 m，流速达到1.5 m/s，海况较为恶劣，波流联合作用下水质点与莫里森单元之间的相对运动速度较大，使得整个平台受到较大的水动力。因此，本文设计了采用两侧共四股锚链的平行布局系泊系统，其主要优点是锚链载荷共享程度较高，可以明显降低每股锚链的极限载荷，从而降低系泊系统包括锚固基础的建设成本。针对该系泊系统的造价评估表明其具有较好的经济性。

（3）时域计算分析了系泊系统在不同浪向角下系缆的张力值，结果表明合成纤维缆绳较小的刚度给予了大型框架式渔业平台一定的运动幅度，使得大型框架式渔业平台所受到的水动力在多根缆绳上分布较为均匀，降低了极个别缆绳张力的峰值。缆绳完好状态下缆绳安全系数大于2.0，单缆破断情况下缆绳安全系数大于1.46，满足规范要求。这些结果可为实际工程应用提供一定的依据。