邮轮甲板结构冗余度的可靠性研究

赵 南，吴恒良，胡嘉骏，吴剑国

（1.中国船舶科学研究中心，江苏无锡 214082；2.浙江工业大学，杭州 310023；3.深海技术科学太湖实验室，江苏无锡 214082）

0 引 言

结构冗余度（Redundancy）是指结构系统在某些构件受损或失效后能继续承受外载荷的能力。它是评估受损结构系统安全性的一个重要指标。按照传统的设计方法，船舶与海洋结构物的冗余度隐含在对结构形式、构件尺度、材料选择、焊接质量等规定中。一般认为满足规范要求的海上结构物在具有足够强度储备的同时也就具有了足够的冗余度。但是近年来，一系列因冗余度不足而导致的海损事故使人们认识到这样一个事实：为了结构的安全，需要设置冗余度。它包含两层意思：一是结构物具有超出基本安全需求的富余度；二是结构的备份或替代。

海洋工程结构冗余度研究的起因可追溯到1980 年Alexander L.Kielland 号平台严重海损事故，由于一根关键承力支柱的疲劳破坏导致一系列相邻支柱的连续失效，致使该平台在20 分钟内倾覆沉没，造成人员及财产的重大损失。这次事故使人们认识到结构冗余度在海洋工程结构物设计与维护中的重要性。20世纪八九十年代，共有约170艘散货船失事和1300余名船员遇难，对海上结构特别是船舶结构的冗余度评估再一次提出了迫切的要求。在2009 年召开的IACS MSC86 会议上首次指出结构冗余度是新船建造标准的功能性要求，这意味着船体结构冗余度已成为结构安全性研究的重点内容。

邮轮作为一个超大载体，为旅客提供食宿、休闲、娱乐等多方面的服务，是名副其实的海上度假村。为了不断丰富并满足旅客多样化的需求，邮轮向着大型化、多功能化不断发展，由此带来巨大经济效益的同时，也对邮轮航行性能以及船体结构强度设计提出了更高的要求。由于环境载荷、工作载荷以及意外事故等多种原因，邮轮结构将不可避免地受到不同程度的损伤，因此，完善结构的设计使其具有足够的安全裕度就显得尤为重要。

目前针对冗余度衡准和方法的研究，大都是针对离散型结构系统提出的，对于船舶与海洋工程结构的加筋板这类连续型组合结构的极限承载能力、局部受损对整体承载能力的影响等诸多影响结构冗余度的因素缺乏明确认识。Frangopol等[1]以损伤可靠性相关的知识定义了冗余度；Chen等[2]通过引入结构系统失效的概念以及可靠性指标的概念，提出了一种分析结构冗余度的新方法；Deco 等[3-4]提出了基于船体弯曲强度概率的结构冗余度评估方法，还提供了一份在不同海况、航向和腐蚀作用下的船舶结构可靠性和冗余度的全面性研究报告；Saydam 等[5]提出了一种在不同工况下船体突发损伤性能评估的概率框架，在冗余度方面对船体的性能进行量化，评估了完整和受损船体的纵向弯曲能力；Zhu 等[6]对瑞利分布的荷载效应进行更新，提高了对船舶横断面的冗余度评估的准确性；陈鹏等[7-8]基于冗余技术的并行原理，在三舱段分析模型的基础上，进行油船和单舷侧散货船舷侧局部结构失效路径判断，运用后屈曲理论和非线性有限元方法，把储备冗余度因子作为结构冗余度的表达形式。

本文以邮轮甲板结构为研究对象，基于结构冗余度准则构造邮轮甲板结构冗余度可靠性计算的极限状态方程，通过逐步迭代法得到加筋板损伤前后的极限承载力；采用一次二阶矩法计算一艘极地邮轮上层建筑在不同参与度时邮轮甲板结构冗余度的可靠性指标和失效概率，并进行相互比较，得出失效概率最大时的上建参与程度。

1 冗余度的极限状态方程

以冗余度准则[9]作为极限状态方程：

式（1）也可表示为

式中，UI、UD分别表示完整加筋板和局部损伤加筋板极限承载力，σI为“100%的静载+100%动载”作用下的完整状态工作应力，σD为“100%的静载+80%动载”作用下的损伤状态工作应力，Uc表示按照规范计算得出的加筋板极限承载力。所以式（2）亦可表示为

令变量X1:UD/UI表示局部损伤结构和完整结构的能力之比，变量X2:Ms表示静水弯矩值，变量X3:Mw表示波浪弯矩值，变量X4:Uc表示加筋板极限承载力的规范计算值，变量X5:σs表示静水弯矩作用下的甲板结构的应力，变量X6:σw表示波浪弯矩作用下的甲板结构的应力，得到甲板结构冗余度的极限状态方程：

2 加筋板极限承载力计算的逐步迭代法

加筋板极限承载力计算通常采用非线性有限元方法，基于“3跨5筋”模型[9]，见图1，虽然这种方法准确率高，但建模和计算时间长。也有较之简化的“1 跨1 筋”模型[8]，见图2。本章在有限元分析的基础上，构造损伤扶强材单元承载能力计算公式，提出损伤加筋板极限承载力的逐步迭代法，为其概率特性计算打下基础。

图1 加筋板应力变形云图Fig.1 Stress and deformation cloud diagram of stiffened plate

图2 扶强材应力变形云图Fig.2 Stress and deformation cloud diagram of stiffener

2.1 拟合扶强材柔度和承载力比值关系式

针对完整、断裂和局部永久变形三种状态下的“1 跨1 筋”扶强材单元，采用非线性有限元方法开展不同柔度系数下扶强材极限承载力计算，其中15 个加筋板的计算结果列于表1。基于此结果拟合出扶强材断裂和局部永久变形两种状态下，承载力比值与扶强材柔度的关系曲线，见图3。

根据拟合的柔度和承载力比值的关系，结合塑性修正，得出扶强材断裂临界应力σbc1和局部永久变形的临界应力：

表1 极限承载力对比结果Tab.1 Comparative results of ultimate bearing capacity

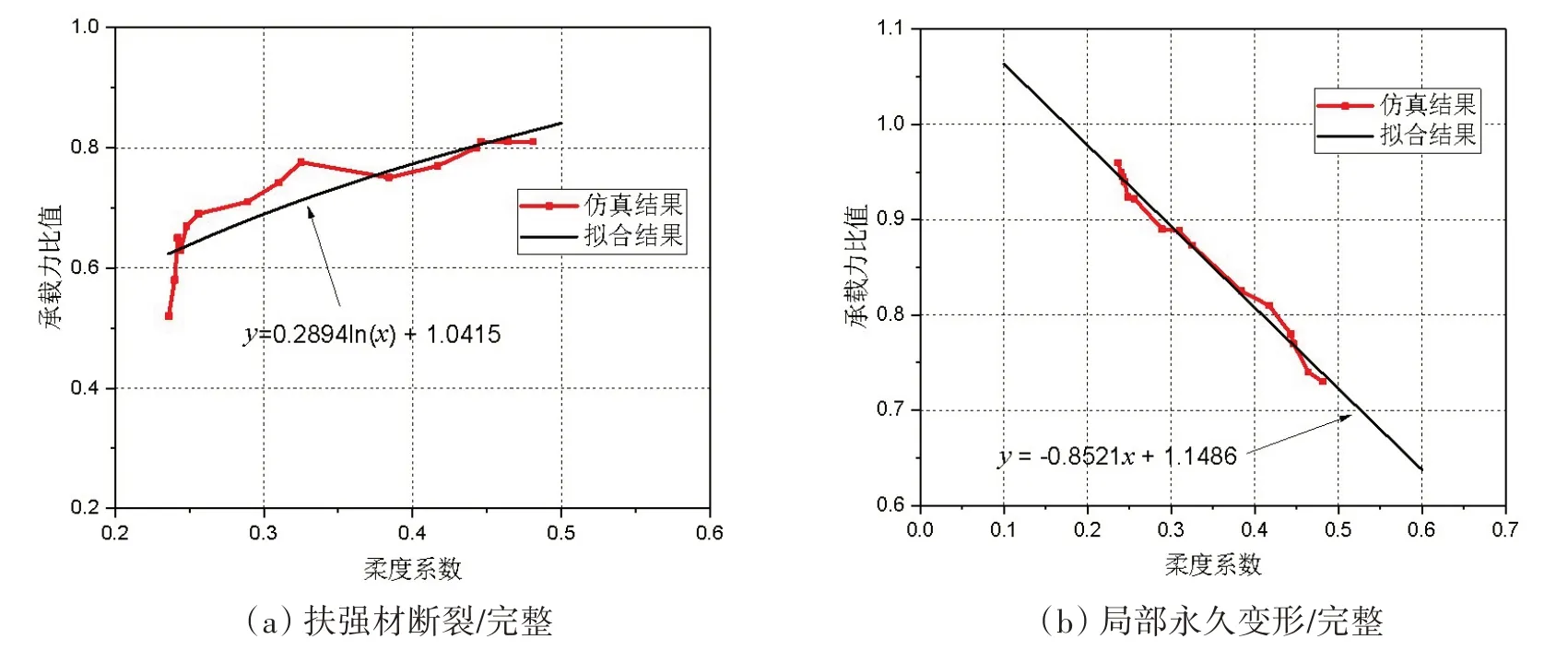
图3 极限承载力比值和扶强材柔度的关系图Fig.3 Relationship between the ultimate bearing capacity ratio and the flexibility

式中，σc1为完整扶强材临界应力，公式如下：

式中，ReHB为单元的等效最小屈服应力，单位为N/mm2；ε为相对应变，ε=εE/εY，σE1为欧拉应力，计算公式详见规范[10]。

2.2 梁柱屈曲的应力应变关系

参照2021 版《钢质海船入级规范》[10]附录5 船体梁极限弯曲能力2.3.4 节梁柱屈曲计算公式，扶强材单元梁柱屈曲的应力-应变关系由下式得出：

式中，As为扶强材的净剖面积，单位为mm2；Ap为带板的净剖面积，单位为mm2；Φ为边缘函数,详见规范[10]：ApE为带板宽度为bE时的净剖面积，单位为cm2。

2.3 损伤加筋板极限承载力计算的逐步迭代法

损伤加筋板的极限承载力计算采用“5筋”模型[9]，即假定加筋板由5根筋（扶强材）组成，仅中间的一根扶强材出现损伤，其他4根扶强材保持完整。假设加筋板在轴向压力的作用下保持平截面，即所有5个扶强材单元的端缩相同；损伤扶强材的应力-应变关系同完整扶强材，只是用临界应力公式（5）替代公式（6）中的σc1。由此构造出含损伤的加筋板结构极限承载力计算的逐步迭代方法如下：

（1）设定一端缩量，即具有一定量的应变。

（2）分别按照完整和损伤扶强材的应力应变关系，计算5 根扶强材单元的应力，乘以其截面积获得每根扶强材单元的压力，累加5根扶强材压力，获得加筋板结构的总压力。

（3）逐步增加端缩量，重复步骤（2），直至获得加筋板压力的最大值，即为损伤加筋板的极限承载力。

基于上述逐步破坏法和“3跨5筋”模型的非线性有限元法，针对不同邮轮甲板结构开展极限承载能力计算，相应的结构尺度参数和计算结果列于表2中。通过对比可以看出，本文所提逐步迭代法与商用有限元软件的计算结果十分接近，表明本文所提逐步迭代法对于损伤状态加筋板结构极限承载力计算具有足够的精度，可用于工程计算。

表2 加筋板参数及损伤前后的极限承载力比较Tab.2 Parameters of stiffened plate and comparison of ultimate bearing capacity before and after damage

3 概率特性参数确定

3.1 损伤前后极限承载力比值概率特性

选取一艘极地邮轮46组典型加筋板结构，采用本文所提逐步迭代法计算了损伤前后各加筋板结构的极限承载能能力（由于篇幅限制，此处不详细列出各加筋板结构尺度及相应结果信息），并进行相应的统计分析，获得损伤和完整状态下极限承载能力比值X1的统计特性，其中均值μX1=0.936，标准差σX1=0.056。

3.2 静水弯矩概率特性

静水弯矩X2的均值和标准差可通过下式计算[11]，静水弯矩概率特性见表3。

表3 静水弯矩的概率特性Tab.3 Probabilistic characteristics of hydrostatic bending moment

式中，Msw0是静水弯矩设计值；νsT、νsT0分别是船舶在一段营运时间T及设计寿命T0（25年）内一种特定载荷状况的发生次数，假设在使用期限内载荷的发生次数为108次，即νsT0=108。

3.3 波浪弯矩概率特性

波浪弯矩X3具有长期的不稳定性，主要来源有海况发生概率、波浪谱型、有义波高和载荷传递函数等，波浪弯矩的平均值和标准差可用以下方程式[12]来估计，波浪弯矩概率特性见表4。

式中，N是船舶运行过程中的波周期数，取108；Mw0是波浪弯矩规范计算值，单位为kN·m。

表4 波浪弯矩的概率特性Tab.4 Probabilistic characteristics of wave bending moment

3.4 加筋板极限强度的概率特性

本文将材料的厚度和弹性模量E作为随机变量处理。假设厚度分布服从正态分布，弹性模量E服从对数分布，详细参数见表5。采用改进罗森布鲁斯（Rosenblueth）法[13]求解其均值和标准差，获得邮轮甲板结构极限强度概率特性，见表6。

表5 与极限强度相关的随机变量概率特性Tab.5 Probabilistic characteristics of random variables associated with ultimate strength

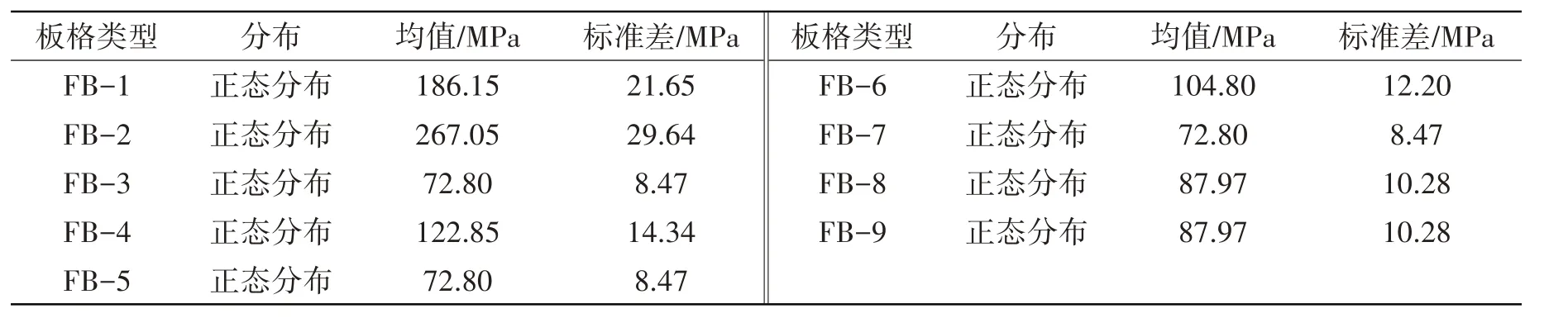
表6 完整甲板结构极限强度的概率特性Tab.6 Probabilistic characteristics of ultimate strength of complete deck structure

3.5 静水和波浪作用下甲板结构应力概率特性

取该邮轮中部33#肋位到66#肋位的舱段结构建立有限元模型，采用有限元软件进行应力分析，获得邮轮甲板结构在上层建筑不同参与度时受到的压应力，分别计算静水弯矩和波浪弯矩作用下压应力σs和σw的概率特性。σs和σw的概率特性由式（12）计算获得，相应的结果见表7 和表8。限于篇幅仅列出中垂弯矩作用下结构的应力与变形图，3 层甲板及以下结构参与总纵强度见图4（a）；4 层、5层、全部甲板及以下结构参与总纵强度时应力与变形图见图4（b）～（d）。

表7 静水弯矩作用下甲板压应力的概率特性Tab.7 Probabilistic characteristics of deck compressive stress under hydrostatic bending moment

表8 波浪弯矩作用下甲板压应力的概率特性Tab.8 Probabilistic characteristics of deck compressive stress under wave bending moment

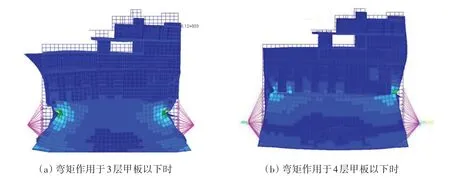
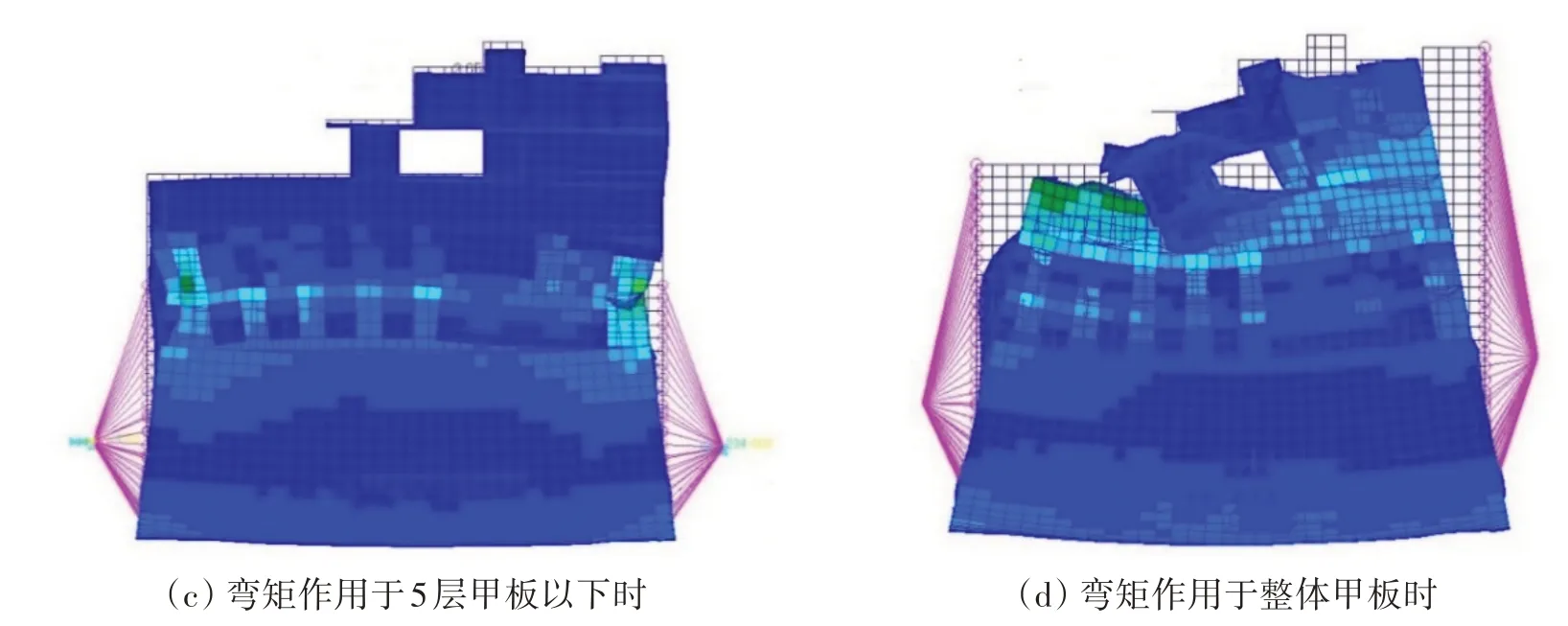
图4 舱段结构应力与变形图Fig.4 Stress and deformation diagram of hold cargo

4 极地邮轮甲板结构冗余度的可靠度计算

以结构冗余度准则作为可靠度的极限状态方程，采用一次二阶矩法，进行上层建筑不同参与度时各种类型甲板结构冗余度的可靠度计算，获得甲板结构的可靠性指标β及失效概率，见表9；将其绘制成图5，同时给出了上建不同参与度时甲板结构的最大失效概率，见表10。

图5 各类型加筋板失效概率Fig.5 Failure probability of each type of stiffened plates

表10 上层建筑不同参与度时甲板结构的最大失效概率Tab.10 Maximum failure probability of deck structure with different participation degrees

由图5和表10可知，随着上层建筑参与程度的提高，结构最大失效概率所在甲板的层数随之上升，总体最大失效概率随之下降。对于中垂状态，当上层建筑不参与总纵强度时，位于3 层甲板的FB-5 加筋板的失效概率最大。位于3 层甲板的FB-5加筋板，是结构主要承受压力的区域，由于参与抵抗总纵强度的结构最少，所以失效概率最大。当4 层甲板及以下结构参与总纵强度时，第4 层甲板是结构主要承受压力的区域，位于4层甲板的FB-6加筋板失效概率最大。由于参与总纵强度的结构增加，第4层甲板上的FB-6加筋板受到的压应力要比上层建筑不参与总纵强度时FB-5加筋板稍小，所以最大失效概率也会稍小。当5层及以下甲板及以下结构参与总纵强度时，第5层甲板是结构主要承受压力的区域，位于5层甲板的FB-7加筋板失效概率最大。由于参与抵抗弯矩的结构不断增加，第5层甲板上的FB-7加筋板受到的压应力也要比4 层甲板及以下结构参与总纵强度时FB-6 加筋板稍小，所以最大失效概率也会稍小。当所有上层建筑参与总纵强度时亦是如此。

对于中拱状态，无论上层建筑的参与程度多少，1 层甲板上的FB-1 和FB-2 始终都是承受压应力的主要区域，但由于加筋板未考虑侧向荷载的作用，所以加筋板的失效概率较小，且随着上层建筑参与程度的提高而下降。

5 结 论

本文构造了邮轮甲板结构冗余度可靠性计算的极限状态方程，提出了损伤加筋板结构极限承载力计算的逐步迭代法，获得了邮轮甲板结构的极限强度、波浪弯矩和静水弯矩等随机变量的概率特性，采用一次二阶矩法计算了极地邮轮上层建筑在不同参与度时，甲板结构冗余度的可靠性指标和失效概率，结果表明：

（1）本文所提出的损伤状态加筋板结构极限承载力计算的逐步迭代法具有足够的精度，计算简便，可应用于工程结构分析。

（2）对于具有较多上层建筑的邮轮结构，随着上层建筑参与程度的提高，结构最大失效概率所在甲板的层数随之上升，最大失效概率随之下降。就极地邮轮甲板结构而言，即便不考虑上层建筑参与总强度，仍具有足够的冗余度，表明该邮轮结构设计是偏安全的。