中等水深10MW张力腿浮式风机基础设计及结构动力特性研究

韩彦青，巩庆涛，徐胜男，楚胜涛

（1.鲁东大学a.水利工程学院；b.蔚山船舶与海洋学院，山东烟台 264025；2.天津大学水利工程仿真与安全国家重点实验室，天津 300350；3.山东省海上航天装备技术创新中心，山东烟台 264004）

0 引 言

我国东南部沿海地区经济发达，但能源紧缺。开发海上风能资源，有效改善能源供应和环境问题，已成为我国“30·60”目标中能源战略转型的一项重要内容。为了更大程度上地利用海上风能资源，《能源技术革命创新行动计划（2016-2030年）》已将远海深水风电场设计建设技术及大型浮式海上风电机组基础设计建设技术列为未来重要的创新突破方向。

目前，我国对于海上浮式风机的研究与规划仍处于初期阶段。与欧美等国家近海水深大（大部海域水深在100 m 以上）相比，我国近海大部海域水深较小，从风电场选址水深方面考虑，我国浙江、福建、广东等省东南部离岸100 km 以内、中等水深（50～100 m）海域适合采用浮式风机发展海上风电[1]，同时这些海域也是风能资源更加集中的区域[2]。从海上浮式风机基础型式方面考虑，张力腿式基础和半潜式基础吃水较小，安装水深灵活，较为适宜于我国东南沿海中等水深海域。相对于半潜式浮式风机，张力腿式浮式风机通过基础（支撑平台）产生大于结构自重的浮力及系泊系统预张力平衡来保持稳定，其受外界载荷所引起的运动幅度小，风机发电较为稳定，并且不需要分散、复杂的系泊系统和压载系统，但技术难度相对较大。国外有美国可再生能源实验室[3]、麻省理工学院[4]、挪威科技大学[5]、GICON公司[6]等，国内有上海交通大学[7]、哈尔滨工业大学[8]、天津大学[9]、江苏科技大学[10]等科研机构学者陆续开展了张力腿式浮式风机的相关研究，提出了多种概念模型，部分项目正在规划建设兆瓦级样机阶段。

海上张力腿式浮式风机主要由风电机组、塔筒、基础（支撑平台）及系泊系统四部分组成。浮式风机的设计水深是一个重要的参数，它影响着系泊系统长度、刚度和基础的吃水、排水体积等主要参数的确定，进而影响到浮式风机的运动与结构内力响应。美国麻省理工学院Sclavounos等[11]研究了不同水深下张力腿式浮式风机基础运动、系泊系统的静力和动力以及作用在锚上的最大张力等参数，研究指出随着水深的减小，浮式风机基础运动响应将会增大，甚至可能不能满足设计要求。Bachynski[12]研究了100 m、150 m 及200 m 水深下张力腿式浮式风机典型固有周期的变化，发现随着水深的增加，基础横荡/纵荡、垂荡周期明显增加，这些运动关系着发电的波动性及支撑结构寿命。特别是在水深较小时，张力腿系泊系统设计尤为关键，非线性影响也更加明显。

为了深入研究张力腿式浮式风机的动力特性，学者们建立了相对完善的时域动力分析模型。美国可再生能源实验室NREL[3]、挪威科技大学Moan教授课题组[12]等多个科研机构基于多体动力学提出了浮式风机空气动力-水动力-结构动力-控制系统耦合的数值分析方法，可以考虑到浮式风机复杂的非线性及瞬时动力特性，如张力腿浮式风机在随机风浪载荷下的动力响应，风机变桨故障停机对塔筒、基础产生的冲击效应等[13]。另外，张力腿式浮式风机不同部位的结构固有振动频率不同，范围可以从0.02 Hz（基础纵荡频率）到5 Hz（二阶基础纵摇、塔筒弯曲振动频率）。这些结构振动频率可能与波浪频率或者叶轮转动频率1P和叶片通过频率3P相近产生共振响应，导致结构损伤发生破坏。张力腿浮式风机在外界风浪载荷作用下将会表现出复杂的结构动力学特性。

因此，针对我国东南部海域中等水深特点设计的张力腿浮式风机，基础（支撑平台）和系泊系统等结构主要参数的设计及中等水深条件下张力腿浮式风机结构动力响应的影响仍需更加深入的研究。本文基于我国东南部中等水深海域环境及载荷特点（本文以60 m 为例），提出一种小水线面、浅吃水、可自浮整体拖航运输安装的张力腿浮式风机结构。通过对结构主尺度参数的优化分析，选择适宜的基础结构形式及尺寸，并对其在工作海况和极端海况下的结构非线性动力响应进行研究，验证其适宜性。

1 张力腿浮式风机基础形式

本文提出的海上张力腿浮式风机基础形式设计理念如下：（1）在位状态下，基础的水线面面积小，主要结构淹没在水面下一定深度，使基础受波浪载荷小（具有较优的水动力性能），同时，较小的水线面也使得在大潮差海域极端水位的变化不会引起较大的系泊载荷变化；（2）在位状态下，基础通过张紧系泊与海床相连，整体运动性能较好，结构内部受力较小，发电稳定（较优的动力特性）；（3）基础吃水小，适用水深范围较广；（4）整机拖航运输工况下，基础吃水较浅，可连同上部风机一起整体浮运拖航，浮运拖航稳性由基础在拖航状态下较大的水线面提供（以增加施工安全性、减小施工安装成本）。

鉴于以上设计理念，本文提出一种小水线面、浅吃水、可自浮整体拖航运输安装的张力腿浮式风机基础结构形式，如图1 所示。浮式风机由DTU-10 MW 海上风电机组[14]、塔筒、基础结构和四组张紧的系泊缆绳组成，其中，风电机组及塔筒的主要参数如表1所示。

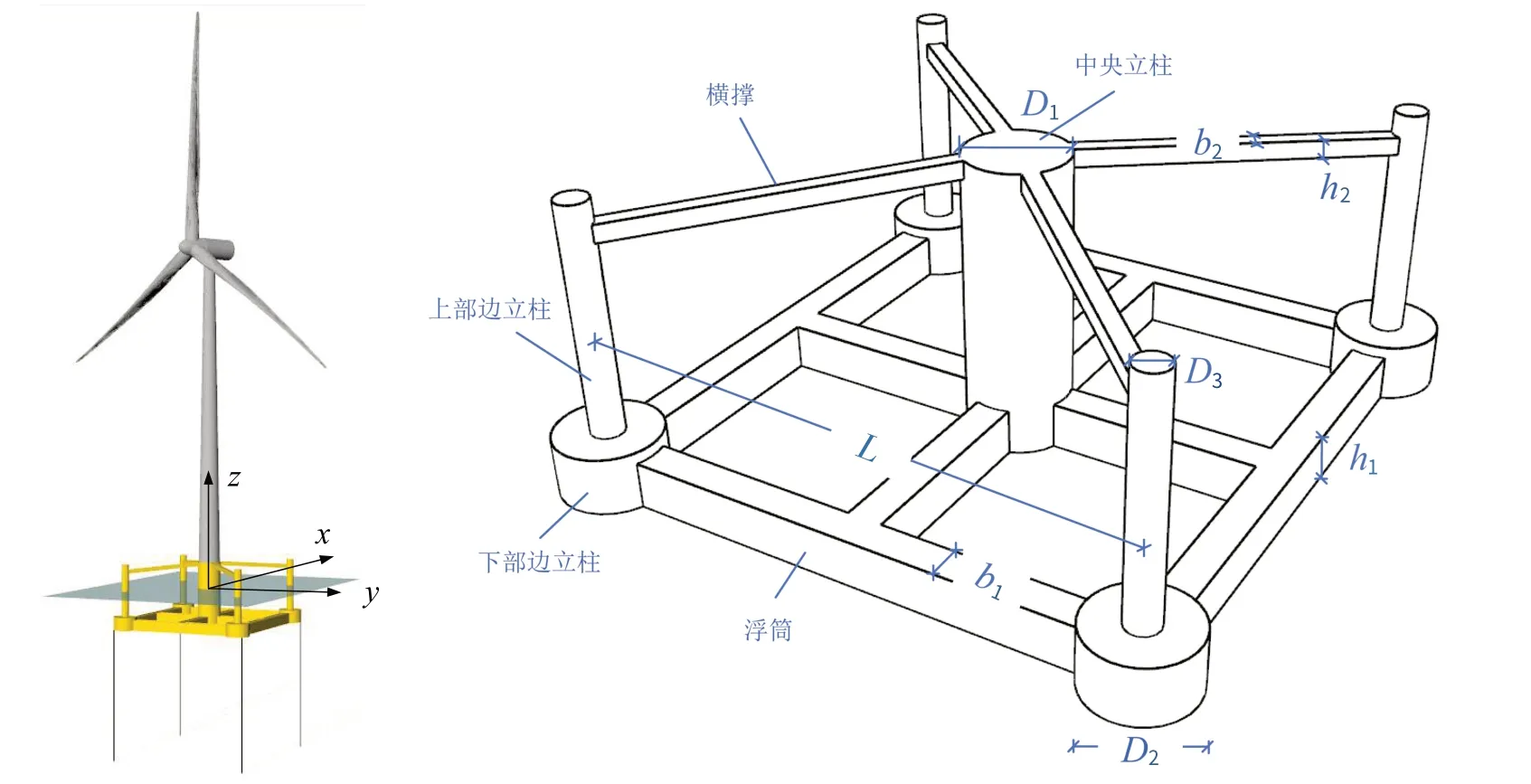
图1 张力腿浮式风机及基础结构示意图Fig.1 Schematic layout of the TLP wind turbine

表1 DTU-10MW海上风电机组及塔筒主要参数Tab.1 Main parameters of the DTU-10 MW wind turbine

基础结构的主尺度参数、质量、排水体积和系泊预张力参数为本文的主要设计优化内容。基础结构形式是在文献[15]潜式张力腿浮式风机基础形式上进行优化后得到的，如图1所示，包括中央立柱、下部边立柱、上部边立柱、浮筒和横撑，其中中央立柱顶部与风机塔筒底部相连，具体尺寸参数符号见表2。

表2 基础结构主尺度参数符号表示Tab.2 Symbols of the main dimension parameters of the floating foundation

2 设计参考依据

在深入分析相关文献及设计规范的基础上，提出了适用于本文中张力腿浮式风机基础结构设计参考依据：

（1）单位兆瓦钢材质量

材料用量在一定程度上影响张力腿浮式风机的成本。James 等[16]总结了近年来多个半潜式、Spar式和张力腿浮式风机单位兆瓦钢材的用量，并指出张力腿浮式风机单位兆瓦钢材用量最小。Soares等[17]提出张力腿浮式风机单位兆瓦质量小于225 t的建议（水线面以上和以下钢材厚度分别取0.035 m和0.04 m）。因此，对于10 MW 海上风机，本文设计的张力腿浮式风机所用钢材质量控制在2250 t 以内。

（2）纵荡、垂荡、纵摇周期

为防止基础与一阶波浪载荷发生共振效应，基础纵荡、横荡的自振周期应大于25 s，基础垂荡、横摇、纵摇的自振周期应小于5 s，并避免接近风机运行1 P及3 P频率[12]。

（3）拖航吃水及拖航稳性

可自浮拖航是本文提出的张力腿浮式风机的一个优点。在风机基础尺寸初步确定时，需要考虑其拖航吃水与拖航稳性。在运输安装过程中，张力腿浮式风机整体稳性至关重要，参考海上石油天然气行业及在前期研究[18]的基础上，提出拖航吃水及拖航稳性的设计要求：拖航吃水小于6 m，初稳性高度大于1 m。

（4）其他参考依据

为减小张力腿浮式风机基础的水动力载荷，应使在位时的基础具有较小的水线面面积。考虑到基础后期运行维护平台需求，设计的中央立柱直径应略大于塔筒底部直径（8.3 m）。下部边立柱高度在满足拖航稳性要求下尽量小，使大部分浮体体积潜于静水面一定距离。

3 分析方法及动力模型

3.1 设计参数估算

根据浮式风机基础主尺度、设计吃水、设计水深参数，通过编制计算表格可估算基础质量M、排水体积∇，进而求得系泊系统预张力：

式中，ρ为海水的密度，M为风机系统的总质量。

基础附加质量Aij、静水回复刚度Cij及系泊系统刚度Kij可根据基础主尺度、系泊缆绳截面及材料属性参数近似求得[5,19]，进而通过下式求得不考虑耦合效应基础不同自由度的自振周期Tn：

整机拖航吃水可根据无系泊时的整机质量及水线面面积求得。初稳性高-- ——GMw可通过下式求得：

式中，K为中央立柱底点，B为基础在拖航状态下的浮心，Mw点为稳心，G为整机重心为稳心半径。

式中，IXX为水线面面积关于X轴的二阶矩。

根据设计参考依据对表2中参数进行估算并初步选定基础方案。

3.2 频域分析

基于三维势流理论及莫里森方程，开展张力腿浮式基础频域水动力分析，分析内容包括：附加质量、辐射阻尼和一、二阶波浪传递函数等参数。这些参数都与平台几何形式、入射波频率及方向、与海床和自由液面的距离等因素有关。采用挪威船级社开发的频域水动力软件Wadam[20]建立张力腿浮式基础模型，并计算以上各参数。软件基于三维势流理论和莫里森方程：即在进行大尺度物体波浪载荷计算时采用三维势流理论，对于小尺度细长物体波浪载荷则采用莫里森方程计算。

3.3 时域耦合动力分析模型

张力腿浮式风机在运行过程中会受到环境载荷作用，如风载荷、水动力载荷、系泊系统载荷等。时域耦合动力分析模型可表示为

式中，M为张力腿浮式风机质量矩阵，A为附加质量矩阵，ζ为基础六自由度运动，K为刚度矩阵，Fw为气动载荷，FI为波浪激励力项，Fd为拖曳力项，Fc为辐射阻尼力项，Fm为系泊系统载荷。采用美国可再生能源实验室开发的OPENFAST软件进行建模，并对正常和极端海况下的结构动力特性进行分析，参考我国《海上浮式装置入级规范》[21]等标准，采用湍流风及随机波浪对海况进行模拟，其中湍流风采用根据IEC 61400-3提供的Kaimal风速谱，随机波浪采用Jonswap谱生成，风及波浪作用方向沿图1中的x轴正向，未考虑海流影响，具体海况及环境参数见表3。

表3 海况及环境参数Tab.3 Sea states and environmental parameters

4 研究结果

4.1 参数估算结果

采用表格估算方法对不同水深条件下张力腿浮式风机基础质量、排水体积、系泊系统预张力、自振周期、拖航吃水等参数进行分析计算，确定三种张力腿浮式风机基础方案，其主尺度参数见表4。其中基础方案TLP1与TLP2质量相近，排水体积及预张力相差较大；TLP2与TLP3预张力相近，质量与排水体积相差较大。为了减小水线面面积，将三种方案的中央立柱直径D1选定为9 m。

表4 不同张力腿浮式风机基础方案属性Tab.4 Attributes of the tension leg platform wind turbines

4.2 频域分析结果

本节从附加质量、势流阻尼、一阶及二阶波浪载荷等频域水动力参数对三种张力腿浮式风机特性进行对比分析。

图2所示为三种张力腿浮式风机纵荡、垂荡及纵摇方向附加质量随频率的变化曲线。图2（a）中，浮式风机TLP1、TLP2 的纵荡方向附加质量明显大于TLP3 的纵荡附加质量；如图2（b）所示，TLP1、TLP2的垂荡附加质量小于TLP3的垂荡附加质量，这是由于TLP1、TLP2较大的下部边立柱高度H2、浮筒高度h1及长度（L-D2）能够提供较大的纵荡附加质量，而TLP3中较大的下部边立柱直径D2及浮筒宽度b1则提供了较大的垂荡附加质量。三种张力腿浮式风机纵荡及垂荡附加质量随频率变化较小。图2（c）中，较大的TLP2 纵摇附加质量与其具有较大的排水体积密切相关，且纵摇附加质量随频率的变化更为明显。

图2 附加质量Fig.2 Added mass

图3为三种张力腿浮式风机纵荡、垂荡及纵摇方向势流阻尼随频率的变化曲线。可以看出三种浮式风机各方向的势流阻尼随频率变化的规律类似，但幅值大小略有不同。浮式风机TLP1及TLP2具有较大的纵荡势流阻尼，TLP3则具有较大的垂荡势流阻尼，三种浮式风机纵摇势流阻尼幅值相差不大。

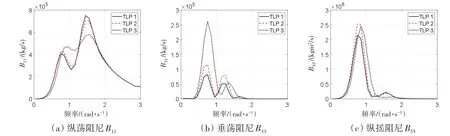
图3 势流阻尼Fig.3 Potential damping

前面提到，本文中张力腿浮式风机在位状态下具有较小的水线面，通过采用基于三维势流理论的频域水动力软件WADAM 计算了三种张力腿浮式风机一阶波浪载荷及二阶和频波浪载荷。由于三种张力腿浮式风机主要结构均在水面以下一定距离，水线面面积大小相同，故纵荡及纵摇方向一阶波浪载荷幅值及变化规律相似，如图4（a）及4（c）所示。由于TLP3中较大的下部边立柱直径D2及浮筒宽度b1，其受到的垂荡方向一阶波浪载荷更加明显，见图4（b）。图5 为浮式风机TLP1 纵荡、垂荡及纵摇方向二阶和频波浪载荷，可以看出，其幅值明显低于一阶波浪载荷。

图4 一阶波浪载荷Fig.4 First-order wave forces

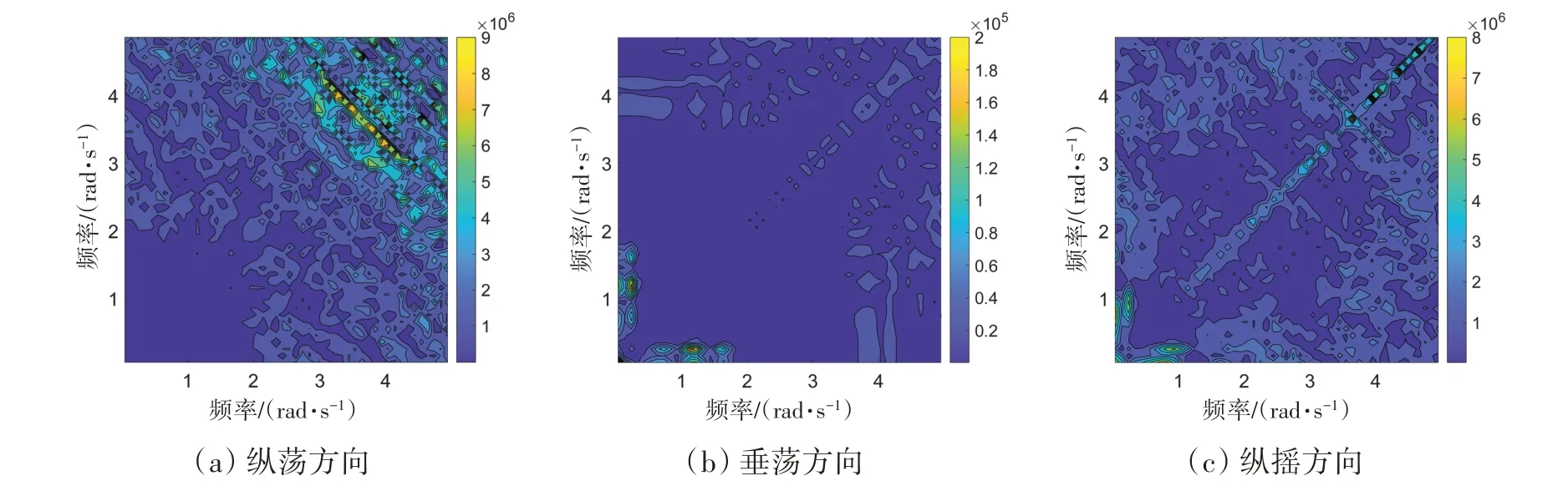
图5 张力腿浮式风机TLP 1二阶和频波浪载荷Fig.5 Second-order sum-frequency wave forces on TLP 1

4.3 时域分析结果

为了研究三种张力腿浮式风机在中等水深下的结构动力特性，本文采用时域耦合分析方法对不同海况下的张力腿浮式风机运动响应、塔筒底部弯矩及系泊系统载荷变化等动力特性进行更加深入的分析，并在时域分析的基础上，进一步对三种张力腿浮式风机的动力特性进行频谱分析。

图6所示为海况LC2下三种张力腿浮式风机动力响应时程曲线，图7所示为不同海况下三种张力腿浮式风机运动响应的统计值，图8 为海况LC2 下张力腿浮式风机运动响应功率谱密度，图9 为海况LC4下张力腿浮式风机运动响应功率谱密度。

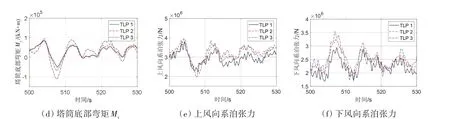
图6 LC2海况下三种张力腿浮式风机动力响应Fig.6 Dynamic responses of the three TLP wind turbines in LC2

从图7（a）～（d）中可以得到，在风机运行正常的海况下（LC1、LC2），张力腿浮式风机TLP1 的纵荡（图7（a）～（b））标准差及最大值均略大于其他两种结构，而在恶劣海况风机停机情况下（LC3、LC4），TLP1 的纵荡（图7（c）～（d））平均值及最大值均小于其它两种结构。这种结果可以通过对比图8（a）及图9（a）分析得到：在风机运行正常的海况下，张力腿浮式风机的纵荡运动主要由风载荷引起，由于TLP1 的纵荡自振频率较其它两个结构小，风载荷引起TLP1 纵荡自振频率下的纵荡运动更加明显，正常海况下浮式风机纵荡频率远离波浪频率，不会发生较大的波频纵荡响应；而在恶劣海况下，由于TLP3的纵荡自振频率较大，更加接近波浪频率，并且其质量及附加质量均小于其它两种结构，更有可能发生较大的波频纵荡运动。如图7（e）～（h）所示，三种浮式风机垂荡统计规律与纵荡类似，即在风机运行正常的海况下，TLP1垂荡较大；在恶劣海况下，TLP3的垂荡更加明显。出现这种现象是因为张力腿浮式风机的低频垂荡响应主要是由纵荡引起的下沉效应（set-down）而产生，在高频处，浮式平台的垂荡自振频率可以很好地避开一阶波浪的频率，不会与一阶波浪发生明显的共振响应；在恶劣海况下，TLP3 较大的波频纵荡引起了更加明显的垂荡响应。三种张力腿浮式风机的纵摇运动规律类似，在正常及恶劣海况下，纵摇运动主要受波浪影响，尤其是对于基础质量及排水体积均较小的TLP3 来说，纵摇运动更加显著。

图7 不同海况下三种张力腿浮式风机运动响应统计特性Fig.7 Statistical values of the TLP wind turbines'motion responses in different LCs

图8 海况LC2下三种张力腿浮式风机运动响应功率谱密度Fig.8 Power spectral densities of the TLP wind turbines'motion responses in LC2

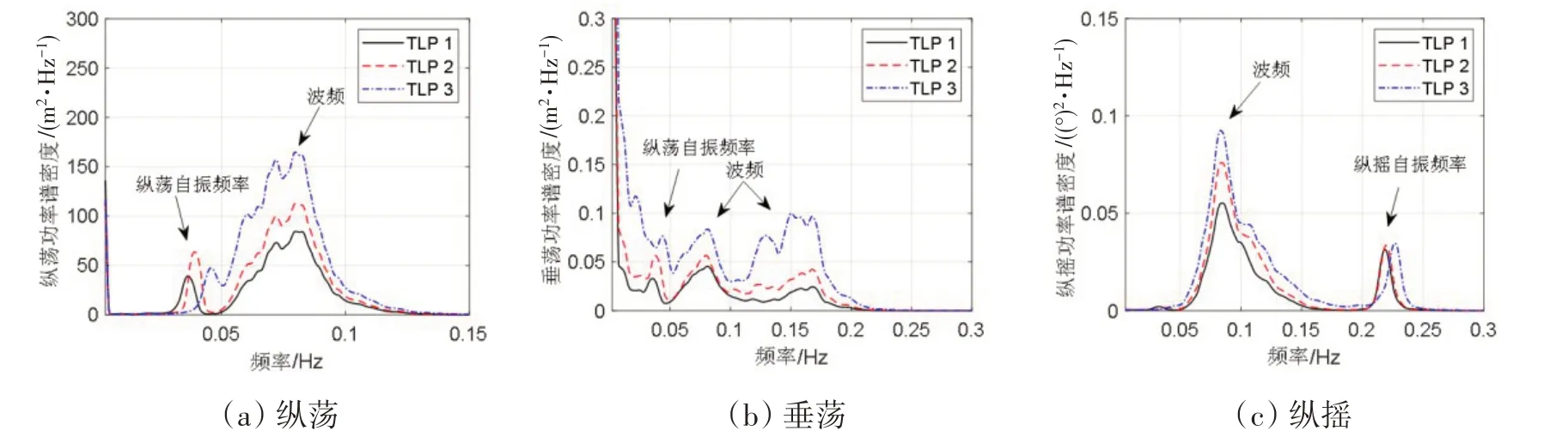
图9 海况LC4下三种张力腿浮式风机运动响应功率谱密度Fig.9 Power spectral densities of the TLP wind turbines'motion responses in LC2

图10所示为不同海况下三种张力腿浮式风机结构内力响应的统计值。图11和图12所示分别为海况LC2和LC4下的张力腿浮式风机结构内力响应功率谱密度。

图10 不同海况下三种张力腿浮式风机载荷响应统计特性Fig.10 Statistical values of the TLP wind turbines'structural responses in different LCs

从图10（a）～（d）中可以得到，在风机运行海况下（LC1、LC2）及恶劣海况下（LC3、LC4），张力腿浮式风机TLP1 塔筒底部弯矩My的标准差及最大值均小于其他两种结构。从图11（a）可以分析得到，在风机运行海况下塔筒底部弯矩My主要受波浪影响，在恶劣海况下My主要受波浪及基础纵摇运动影响，且对于基础质量及排水体积均较小的TLP3影响更加明显。从图10（e）～（h）及图10（i）～（l）可以看出，风机运行海况及恶劣海况下，上下风向系泊张力具有类似的统计规律。这主要是因为上下风向系泊张力均受波浪影响较为明显（图11（b）～（c）），对于基础质量及排水体积均较大的TLP1，其系泊张力较小；在恶劣海况下（图12（b）～（c）），由基础纵摇及垂荡运动引起的系泊张力变得更加显著，尤其是对于TLP3，基础垂荡引起的系泊张力变化比其它两种张力腿结构更加明显。

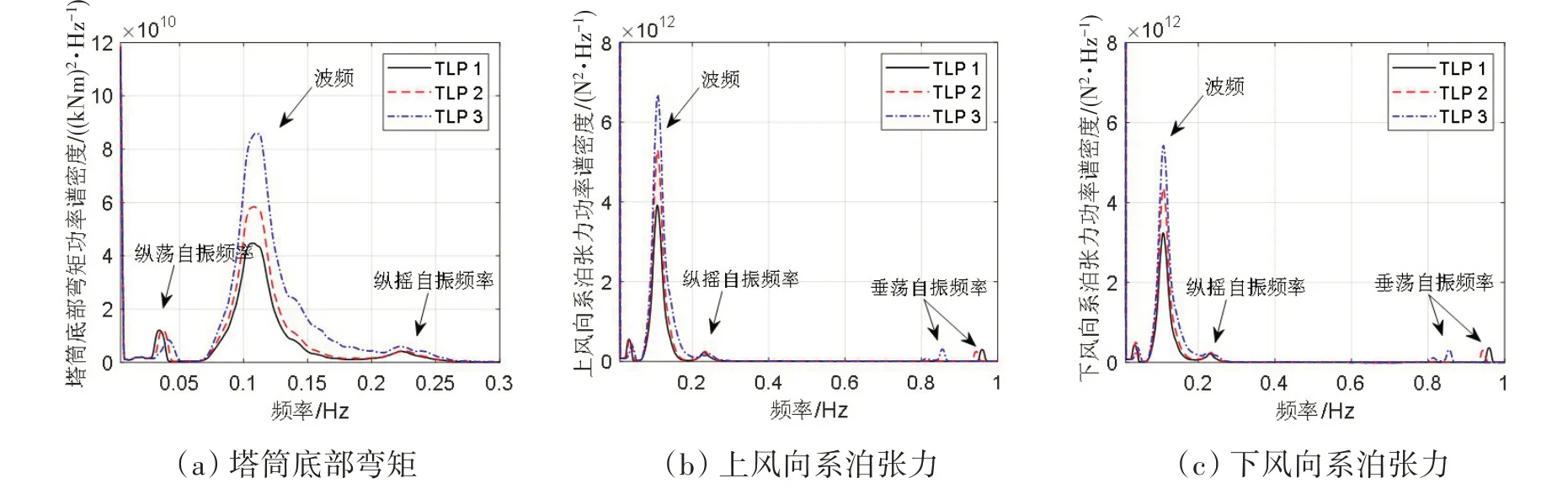
图11 海况LC2下三种张力腿浮式风机结构响应功率谱密度Fig.11 Power spectral densities of the TLP wind turbines'structural responses in LC2

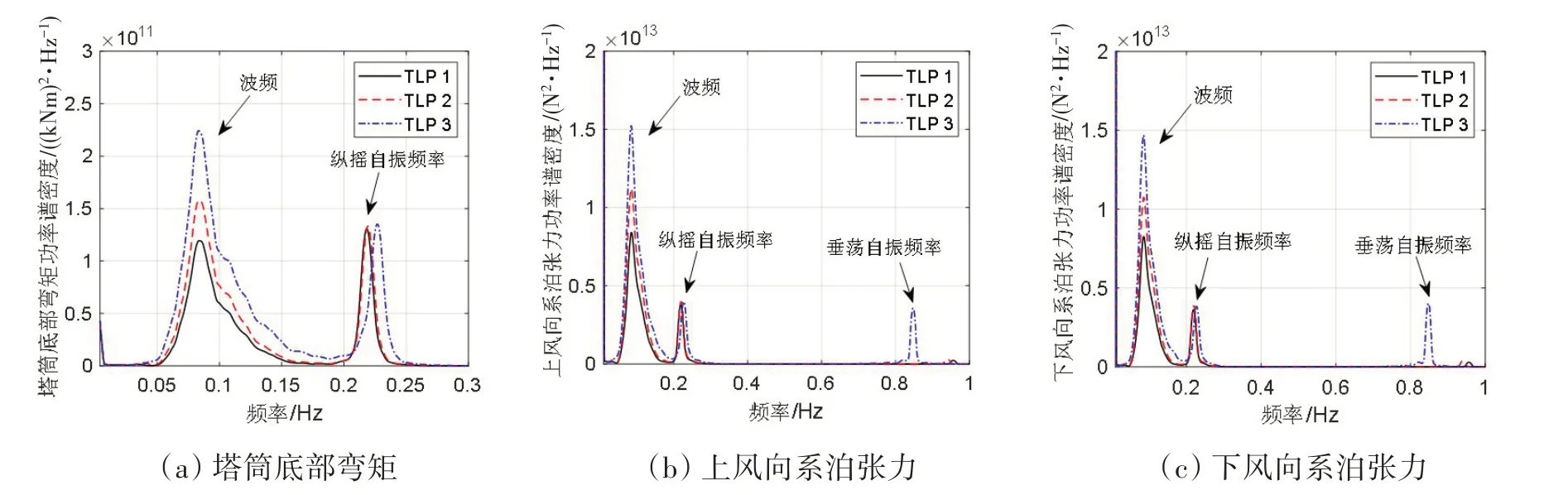
图12 海况LC4下三种张力腿浮式风机结构响应功率谱密度Fig.12 Power spectral densities of the TLP wind turbines’structural responses in LC4

综上所述，张力腿浮式风机TLP1、TLP2 的基础质量及运动自振周期符合设计参考依据；TLP3 的基础质量较小，预张力较大，纵荡自振周期小于25 s，可能与一阶波浪载荷发生共振，产生较大的结构动力响应。通过三种张力腿浮式风机在运行及恶劣海况下的基础运动、塔筒底部弯矩、系泊张力对比分析可以得到，张力腿浮式风机TLP1具有较优的动力性能。

5 结 论

本文针对我国东南部海域中等水深及环境载荷特点，基于某10 MW海上风机，提出了一种小水线面、浅吃水、可自浮整体拖航运输安装的张力腿浮式风机基础结构。通过设计对比分析三种不同主尺度、基础质量及排水体积的张力腿浮式风机结构，得到如下结论及建议：

（1）对于中等水深张力腿的设计，其纵荡自振周期应大于25 s，以避开常见一阶波浪周期。在不增加基础质量的前提下，可以通过加大底部浮筒的高度，减小其宽度，从而增加纵荡的附加质量及势流阻尼。

（2）当张力腿浮式风机基础质量较小（单位兆瓦质量小于180 t）时，可能引起较大的基础运动、塔筒底部弯矩及系泊张力等动力响应。

（3）对于张力腿浮式风机来说，预张力较大导致系泊成本增加，且并不一定得到较优的动力性能，尤其是对于中等水深处张力腿浮式风机，预张力越大，纵荡自振周期越小，可能与一阶波浪载荷发生共振。