新型DBA隔板结构下LNG储罐液体晃荡的数值研究

张茴栋，李 琪，史宏达

（中国海洋大学，山东青岛 266100）

0 引 言

随着国家对清洁能源需求的增加，LNG造船业得以蓬勃发展，其储罐中液体的晃荡逐渐成为船舶研究中的热门问题。液舱晃荡是指部分充满液体的液舱在受到外部激励时，舱内具有自由表面的液体发生剧烈运动的一种现象。当外界激励频率接近液舱的固有频率或者激励振幅较大时，会引起舱内液体发生剧烈晃荡，其产生的冲击压力可能会损坏储罐舱壁，对经济、环境和安全产生不利的影响[1]。因此，提出一种有效的制荡结构对海上作业以及运输安全具有重要意义。

在理论分析方面，Faltinsen 等[2]使用多模态方法（Multimodal Method）建立了矩形液舱中晃荡问题的非线性解析解，因而可以更加准确地预测晃荡对舱壁产生的动压力；Miao 等[3]通过理论方法，分析了内部带有隔板的圆柱体储罐在外界激励下的晃荡荷载问题；Zhang 等[4]基于势流理论和摄动对三维液舱在横荡和纵荡耦合激励下的晃荡问题进行了研究。随着CFD（Computational Fluid Dynamics）技术的成熟和实验结果精度的提升，这为分析晃荡问题提供了更多的方法。

针对内置隔板制荡问题，Liu 和Lin[5]基于Navier-Stokes 方程，运用界面捕捉的方法研究带有竖隔板的液舱晃荡问题；Tang 等[6]则进一步改进了液舱的竖隔板结构，提出一种不均匀挡板高度分配的方案，并论证了挡板高度的分配模式会对液舱晃荡产生显著的影响；Wang等[7]基于线性势流理论详细推导了晃荡问题的SBFEM（Scaled Boundary Finite Element Method）方程，研究了T型隔板中载液率、隔板的排列方式和隔板的长度对晃荡频率、相应的晃荡模态和波幅的影响；Sanapala 等[8]采用数值模拟的方法研究了部分充液的矩形液舱在竖向简谐激励和地震激励下的晃荡动力学问题，得到了挡板的最佳位置和宽度；Xue等[9]通过试验的方法研究了不同的竖直隔板对晃荡压力的影响，试验结果表明，竖直隔板会改变液舱的一阶固有频率，同时降低舱壁处的冲击压力；Jiang 等[10]采用IRF（impulse-response-function）方法和CFD 方法相结合的混合数值模型，研究了不同参数的横隔板对晃荡抑制的效果，结果发现采用多层水平隔板可有效地抑制晃荡响应；Kargbo 等[11]建立了矩形液舱内因密度分层的油水与T 形挡板形式的刚性多孔结构相互作用的数值模型，分析了多孔结构在不同工况下的阻尼效果及对液舱壁面处波面高度和冲击压力的影响。

综上所述，目前大部分工作是针对传统隔板，即横隔板、竖隔板以及T 型隔板所做的研究。为进一步提升装置的制荡性能，本文提出一种新型的DBA（Different Baffle Angle）隔板结构，针对其制荡结构的最优形式开展一系列的数值研究。首先，开展网格无关性验证，确定合适的网格尺寸；其次，通过数值与试验结果的比对，验证晃荡模型的准确性；最后，提出DBA 新型隔板结构，通过液面高度、冲击压强、速度幅值和流动状态分析不同激励条件下液舱的晃荡程度，探寻出隔板制荡的最佳形式。

1 数值模型

1.1 控制方程

流体的运动受到各种守恒定律的控制，最基本的守恒定律包括质量守恒、动量守恒和能量守恒。这些守恒定律都可以采用控制方程进行数学描述。首先，流体必须满足质量守恒定律，即流体单元在单位时间内的质量增加等于在同一时间间隔内流入单元的净质量，其数学表达式可简写为

式中，ρ代表液体的密度，t代表时间，xi和ui分别表示i方向上的空间坐标和速度。其次，流体也必须满足动量守恒定律，可以理解为流体单元中动量的变化率等于作用于这个单元上的各种外力的总和。动量守恒方程又称N-S方程，其表达式为

式中，p为流体压强为网格运动在i方向上的速度分量，μ为流体动力学黏性系数，fi为单位体积流体所受到的体积力，其余变量的物理含义与公式（1）中的完全相同。

本文采用了Lauder和Spalding于1972年提出的标准k-ε模型，该模型由湍流能量k和湍流耗散率ε方程组成：

式中，μ是层流粘性系数，μt=ρCμ k2/ε是湍流粘性系数，Gk是由平均速度梯度引起的湍流能量k的生成项，计算公式如下：

根据Launder等的建议和试验验证，模型常数项取值如下：

1.2 自由液面

本文采用VOF（volume of fluid）方法对自由液面进行捕捉，该方法的基本思想是引入一个流体体积函数αi，其定义如下：

根据体积分数的值，可以判断网格单元中是否存在液体，评判标准如下：

注意，本文将αi=0.5的等值面看作是液舱内的自由液面。

1.3 外界激励及固有频率

为了有效模拟液舱内液体的晃荡，需要对液舱施加一个外界激励。如果外部激励频率接近液舱的固有频率，就会发生共振现象，产生剧烈的晃荡。因此，施加激励前有必要对液舱的固有频率进行计算，对于矩形液舱其计算公式如下：

式中，h为液体高度，L为液舱长度，ωm和km分别代表圆频率和波数，m代表晃荡模态的阶数。当m=1时，对应的ω1是液舱的一阶固有频率。此外，本文中液舱的激励可以表示为

式中，A为振幅，ω为激励频率，t为时间。

1.4 DBA隔板液舱模型

为了抑制液舱的晃荡，学者们对加入横隔板以及竖隔板的液舱做了大量的研究，分析隔板的制荡效果。最近有学者提出可将横隔板与竖隔板进行组合形成T 型隔板，此隔板兼有横隔板和竖隔板的优势且当制荡效果相同时用料更少，结构更轻。在T型隔板的基础之上，本文提出了一种新型的DBA隔板形式，其在液舱中的布置如图1 所示。本文中的算例均采用STAR-CCM+软件进行计算，始终采用P1 点作为压强测点，通过切割体网格生成器来提高生成网格的质量，选择棱柱层生成器对壁面处的网格进行细化处理，设定棱柱层的总厚度为内部网格的5%，棱柱层设定为6层，棱柱层的延伸率设为1.5。此外，STAR-CCM+采用全y+壁面处理，该处理使用混合壁面函数，该函数可以描述三个边界层（粘性底层、缓冲层和对数层）中的速度和湍流，它可以根据输入流速和边界网格自动计算y+值，并自动切换壁面函数[12]。为了更加接近真实环境，本文数值模型中的液舱壁均设置为不可滑移壁面，y+值小于5，并且满足无通量条件。舱内采用欧拉多相流模型，气相和液相分别设定为空气和水，舱内空气压力设定为标准大气压，液舱通过轨迹法实现运动。计算的时间步长设定为0.001 s，时间步长中最大内部迭代次数设定为10。求解方式采用隐式不定常，计算模式采用二阶时间离散。

本文的研究对象为立方体液舱，其边长D为1 m，底部竖隔板和翼缘板的长度分别取为0.3D。定义翼缘板与水平线之间的夹角为θ，在底部竖隔板的高度与翼缘板的长度不变的情况下，随着翼缘板的转动，夹角也会随之不停地改变。理论上θ的可转动范围介于-90°～+90°之间，当θ小于零时，翼缘板将会向下伸展，取-45°的情况进行分析；当θ等于零时，这便是传统的T型隔板；当θ大于零时，翼缘将会向上伸展，取+15°、+30°、+45°、+60°、+75°和+90°（即竖隔板）的角度进行研究。

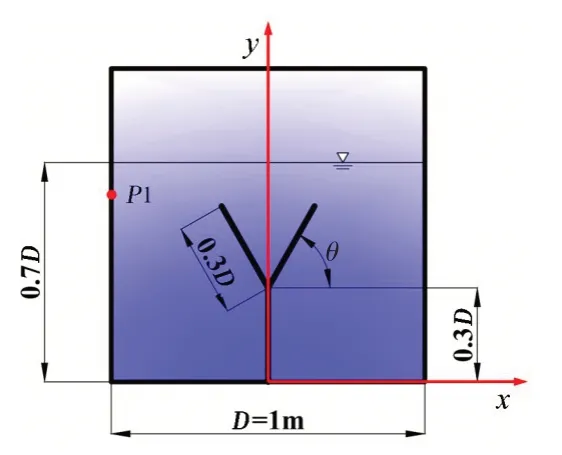
图1 DBA隔板液舱示意图Fig.1 Diagram of DBA baffle tank

2 数值模型验证

首先，开展网格无关性的验证。选取边长为1 m的二维矩形液舱，液深定为0.5 m。考虑不同振幅和激励频率的影响，通过两组典型算例进行分析，具体工况见表1。鉴于Arun和Cho[12]以及Tang等[6]学者的数值模型与本文的研究对象比较接近，参考其网格尺寸划分方法，在满足CFL（Courant-Friedrichs-Lewy condition）条件下，本研究提出如下三种网格：粗网格D1的尺寸为10 mm×10 mm，中等网格D2为5 mm×10 mm，细网格D3为2 mm×4 mm。选择计算稳定后的数据进行对比，如图2所示，基于D2和D3网格得到的结果非常接近，即使采用粗网格D1，其计算精度与细网格D3的相对误差最大也不超过7%，因此，为了保证计算精度和节省计算时间，本文选取D2尺寸的网格开展晃荡的研究。

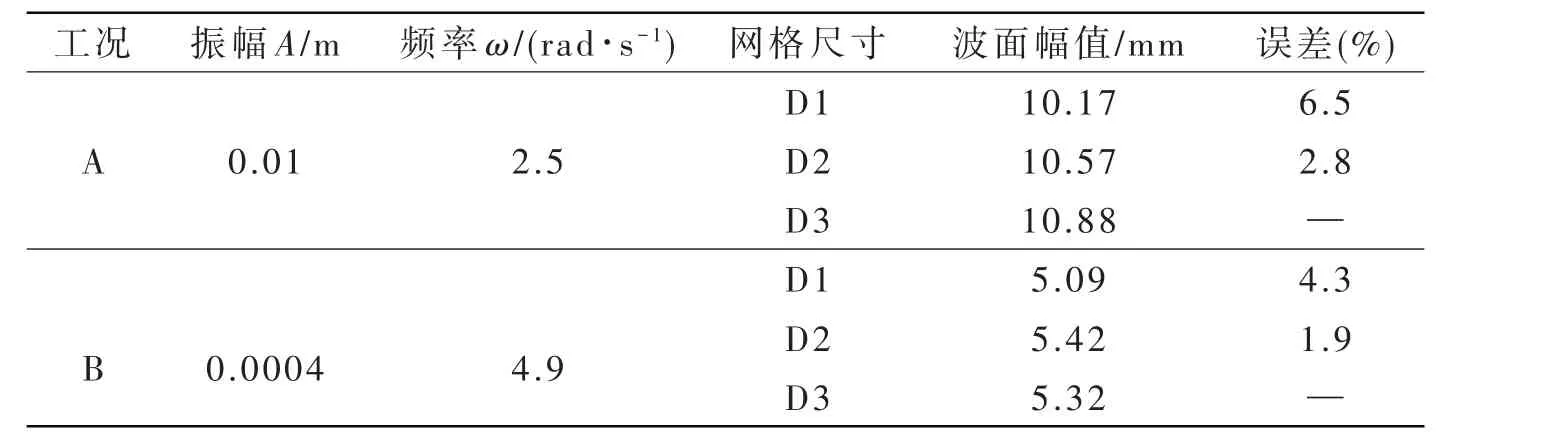
表1 工况和网格无关性验证结果Tab.1 Cases and results of mesh convergence analysis

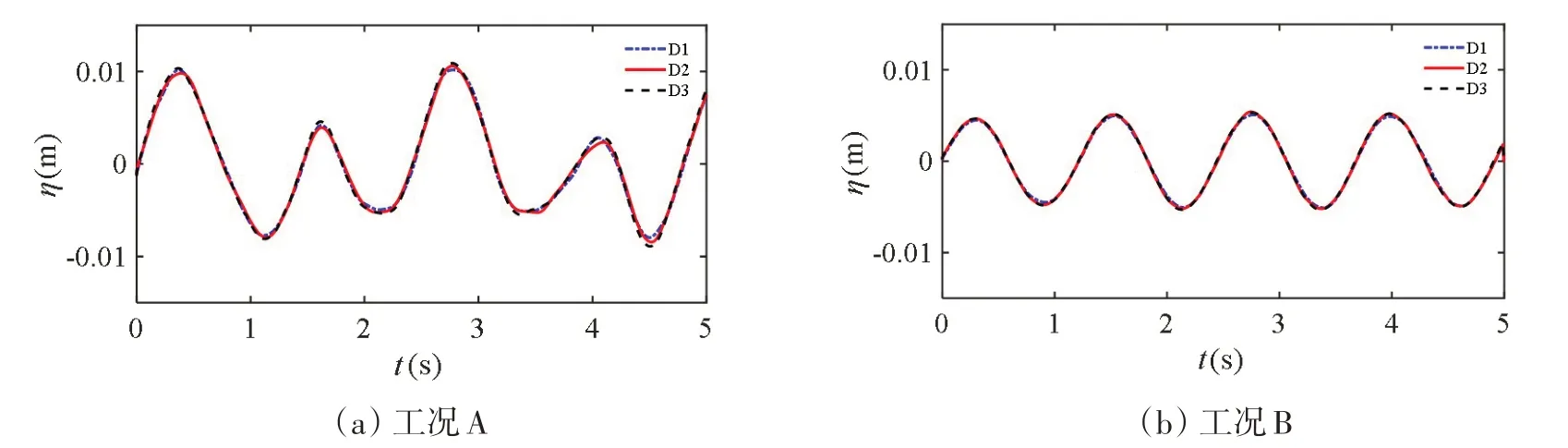
图2 网格无关性验证Fig.2 Mesh convergence analysis

其次，进行模型计算精度的分析。基于Liu 和Lin[5]的物理实验建立数值模型，液舱固有频率ω0=6.0578 rad/s，激励类型为简谐振动，两种工况的激励频率分别取为0.583ω0和1.0ω0，激励振幅均为5 mm，将数值计算结果与实验测量值进行对比，通过图3可知，两者吻合较好，数值模拟精度较高，因而证明了该模型可以用来继续开展液舱晃荡的相关研究。

3 结果与讨论

3.1 DBA隔板对液舱固有频率的影响

本节分析不同DBA 隔板形式对液舱固有频率产生影响的规律。过去的研究表明，一般储罐的装载极限为89.1%[13]，而装载率为70%是最危险的工况[14]。为了验证这一论点，本文将液深分别设置为600 mm（60%）、650 mm（65%）、700 mm（70%）、750 mm（75%）和800 mm（80%），比较不同载液率情况下液舱发生共振时同一测点压强的最小值和最大值，最终发现载液率在70%时，舱壁处的压强峰值最大，液舱处于最危险的状态，因此本文以载液率为70%的方形液舱为研究对象，开展DBA 隔板制荡形式的优化探索研究（图4测点均位于左舱壁初始自由液面下0.1 m处，激励振幅0.01 m）。

图4 不同液深下液舱发生共振时舱壁压强的最大值和最小值Fig.4 Maximum and minimum values of bulkhead pressure when tank resonates at different liquid depths

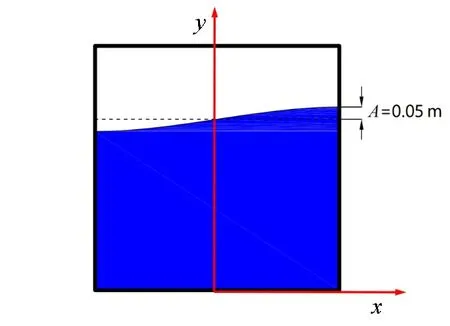
图5 自由液面一阶振型示意图Fig.5 Schematic diagram of the first order mode of free surface

首先对无隔板液舱进行分析，通过数值方法模拟液面的自由衰减试验。在初始时刻给舱内液体设定一个初始液面，舱内液体在因重力引发的晃荡过程中会显示其固有谐振的特征。为了提取该液深下的一阶固有频率，将自由液面设置为一阶振型（波长等于液舱长度的二倍），如图5 所示，自由液面场函数设定为

式中，η0=0.7 m，A=0.05 m，L=1 m。提取左舱壁处的液面时历曲线（图6）并对其进行傅里叶变换得到对应的频谱图（图7）。

从图7中可以观察到频谱有一明显的峰值，该峰值对应的频率即为液舱的一阶固有频率，其大小为5.481 rad/s，与理论解析解相同，因此该数值方法可有效获得液舱晃荡的固有频率。采用同样的方法处理装有DBA隔板的各个液舱，得到的一阶固有频率如表2所示。随着角度逐渐增大，即翼缘隔板逐渐抬升，液舱的一阶固有频率会略微减小，但当角度增大到75°时，液舱的一阶固有频率会突然增大，随后缓慢减小。这一频率突变是由于翼缘板的转动引起的，因为舱内隔板的总高度较大时，整个液舱近似等价为顶部连通的两个小液舱，依据公式（8）可知，长度较小的液舱固有频率应该较大。

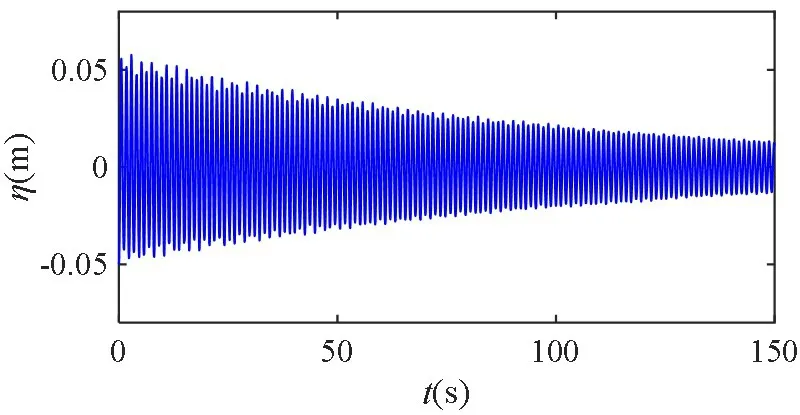
图6 无隔板液舱自由衰减时历曲线Fig.6 Time series of free decay of tank without baffle

图7 自由衰减时历曲线对应的频谱图Fig.7 Spectrum of time series of free decay

表2 液舱一阶固有频率数值解Tab.2 Numerical solution of first-order natural frequency of tank

3.2 DBA隔板对波幅极值的影响

通过比对不同外界激励条件下左舱壁液面的波幅极值，分析DBA 隔板角度对液舱制荡效果的影响。假设液舱受到水平方向的正弦激励，以ω0=5.481 rad/s 为基准，选取一系列的外界激励频率，振幅均设为0.01 m。监测左侧舱壁处的波面时历曲线，提取波幅极值并进行无因次化处理。

通过图8 可知，无隔板液舱、DBA 隔板转角为-45°、0°、15°和30°的液舱在0.85ω0～1.0ω0的频率范围之内出现明显的峰值，这是因为此时外界激励频率接近于四种液舱的固有频率而诱发共振现象，微小的激励振幅也会使舱内液体最终发生剧烈的晃荡；当外界激励频率（1.7ω0）接近五种液舱的高阶模态固有频率时，其诱导产生的最大晃荡幅值与其它隔板类型的液舱差距并不太大。此外，非常明显的是其余四种隔板转角的液舱在所有激励频率的作用下并未出现特别剧烈的晃荡。当DBA隔板转角为60°时，整个激励频率范围内响应的波幅极值均保持在较低的水平，即使该液舱发生了共振现象，其幅值相较于其它类型液舱来说也是较小的，因此，整体来看转角为60°的隔板抑制晃荡的效果最优。

图8 不同激励频率下无因次波高最大值Fig.8 Maximum dimensionless wave height with different exciting frequencies

晃荡是一种液体运动，运动就意味着能量的变化，因而可以从能量的角度来探究隔板对晃荡的影响。鉴于DBA隔板转角为60°的液舱的制荡效果最好，选取最接近其固有频率（即0.78ω0）的激励工况进行分析，提取三种典型隔板液舱（-45°、60°、90°）以及无隔板液舱此时的液高时历曲线并对其进行傅里叶变换。

图9（a）中的能量谱呈现出明显的双峰现象，第一个峰值对应外界激励频率处，第二个峰值出现在液舱的一阶固有频率处。总体而言，能量主要集中在两个峰值的位置，且基本处于同一量级。图9（b）展示出与图9（a）相似的规律，但由于隔板的影响，此时能量开始逐步分散到两个谱峰频率之间的成份上，因而可知此时流场开始变得紊乱。图9（c）展示了转角为60°液舱的频谱图，由于激励频率接近液舱固有频率，此时未能出现双峰现象，二倍频率处的能量也非常少。虽然发生了共振现象，但是翼缘隔板有效地抑制了晃荡的程度，再次证明了DBA 隔板转角为60°时的优越性。图9（d）说明如果外界激励频率远离液舱固有频率，晃荡的能量将主要集中在外界激励频率附近，频谱双峰现象将会消失。

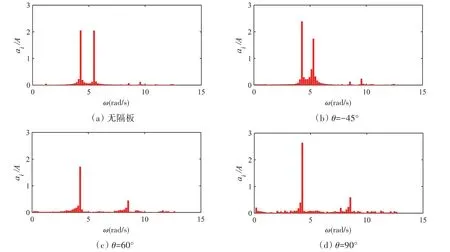
图9 液舱波面时历曲线的频谱图Fig.9 Spectrum of time series of tank surface elevation

3.3 DBA隔板对舱壁压强的影响

液舱晃荡除了会对船舶的稳定性造成影响外，强烈的冲击压力还可能损坏舱壁。因此，本节对液舱晃荡过程中舱壁处的压强进行比较。同时为了进一步论证DBA 隔板转角为60°时最优，压强比较时对其它所有角度的隔板进行了尺寸调整，以确保具有相同的投影面积，如图10 红色方框所示。在左舱壁初始自由液面以下0.1 m 处设置压强监测点，外界激励频率设为4.251 rad/s（接近60°隔板液舱的固有频率）。

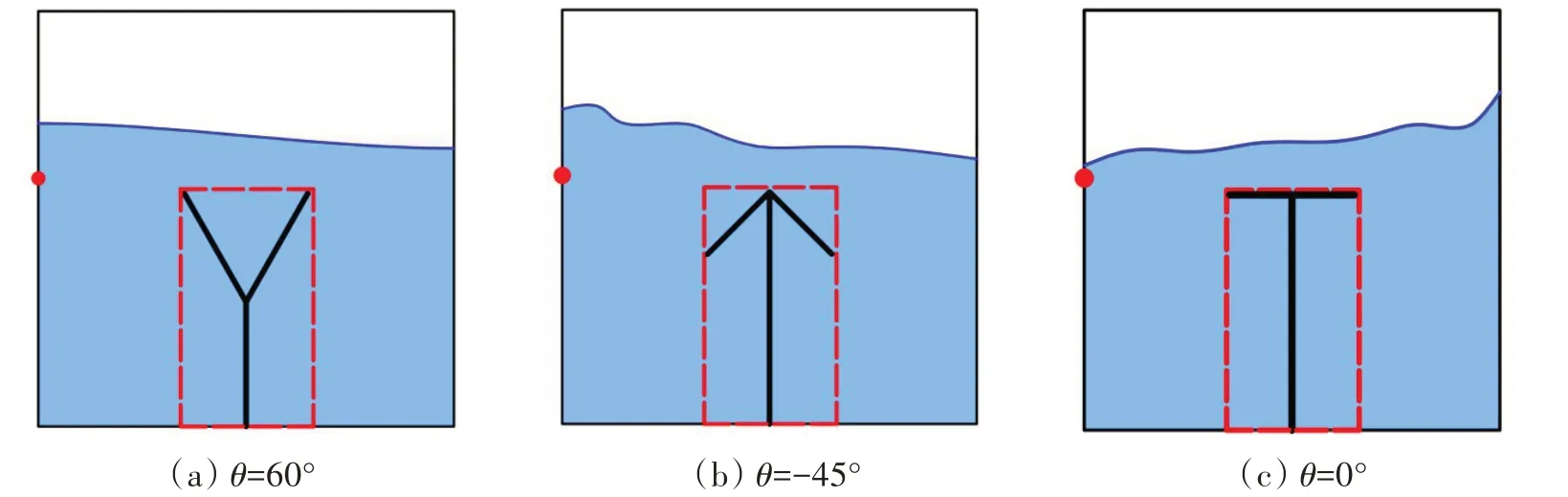
图10 具有相同投影面积的DBA隔板示意图Fig.10 Diagram of DBA baffles with the same projection area

图11（a）展示了不同DBA隔板转角对液舱晃荡强度的影响。可以看出，0°隔板液舱压强的曲线较为规律，而-45°和60°隔板液舱的压强曲线均出现了双峰现象。隔板角度为正时的最大冲击压强远远小于其它两种形式液舱的压强，说明转角为正时隔板的制荡效果明显优于其它两种方案。在图11（b）中，重点分析了不同正向角度的隔板对舱壁处压强的影响，很显然，翼缘板转角小于60°时压强曲线依然保持双峰现象，超过60°时此现象逐渐消失，此外，60°隔板液舱的压强波动幅值始终最小，再次证明其为最优翼展角。

为了更加清晰地展示DBA 隔板对液舱晃荡的抑制效果，可对液舱内流体的速度矢量幅值以及流动状态进行分析研究。图12 选取隔板转角分别为-45°、0°和60°的液舱进行比较，这三种液舱里都出现了大量的漩涡，可有效地消耗能量，达到抑制晃荡的目的。相比于其它两种角度，60°时液舱中流体速度幅值偏大的区域占比较低(见图12(c))，因为此时翼缘隔板产生的涡旋可以最大程度上消耗外部激励传导给液体的能量。当流体与壁面作用的垂直速度分量较小时，因晃荡而引起的冲击压强将会显著降低，这是60°转角液舱的舱壁压强最小的根本原因之所在。

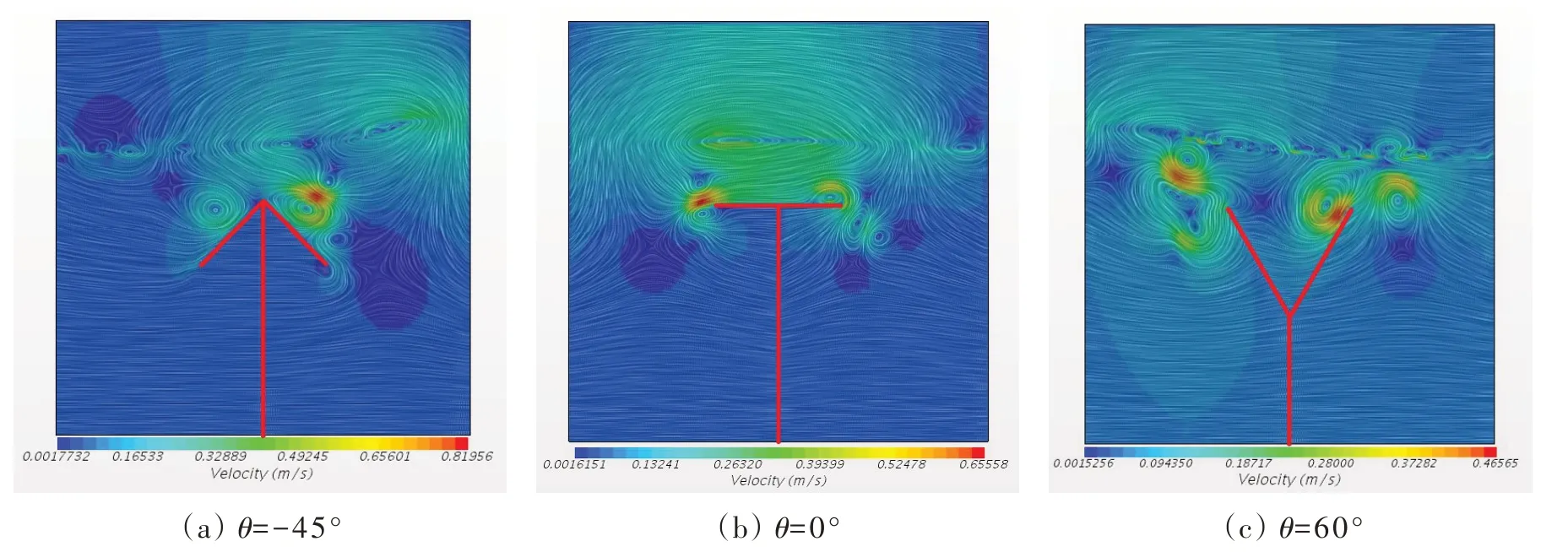
图12 t=5 s时液舱流动状态和速度矢量幅值Fig.12 State of tank flow and amplitude of velocity vector at t=5 s

3.4 DBA隔板构件尺寸对晃荡的影响

鉴于转角为60°的隔板抑制晃荡的效果最佳，以图10（a）中的DBA隔板为基准,下面对其构件尺寸进行进一步的探索研究。保持垂向总高度和翼缘板角度不变，改变底部竖隔板的高度以及翼缘板的长度，可以得到新的四种隔板形式，如图13所示。

设置两种测试工况，激励振幅为0.01 m，激励频率分别取为6.577 rad/s（远离固有频率）和4.251 rad/s（接近固有频率）。在这两种工况下比对调整后隔板液舱和基准隔板液舱的波幅和压强极值，结果如表3和表4所示。工况一中只有第四种隔板（400 mm）的性能优于基准隔板，但此时波幅和压强的极值较小，差距并不明显。工况二的波动幅度更大，此工况下进行对比更有实际工程意义，在隔板总高度和转角不变的情况下，基准隔板即底隔板高300 mm的制荡效果最优。

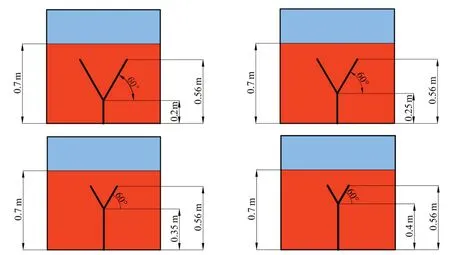
图13 调整后的四种液舱隔板示意图Fig.13 Diagram of four tank baffles with adjustment

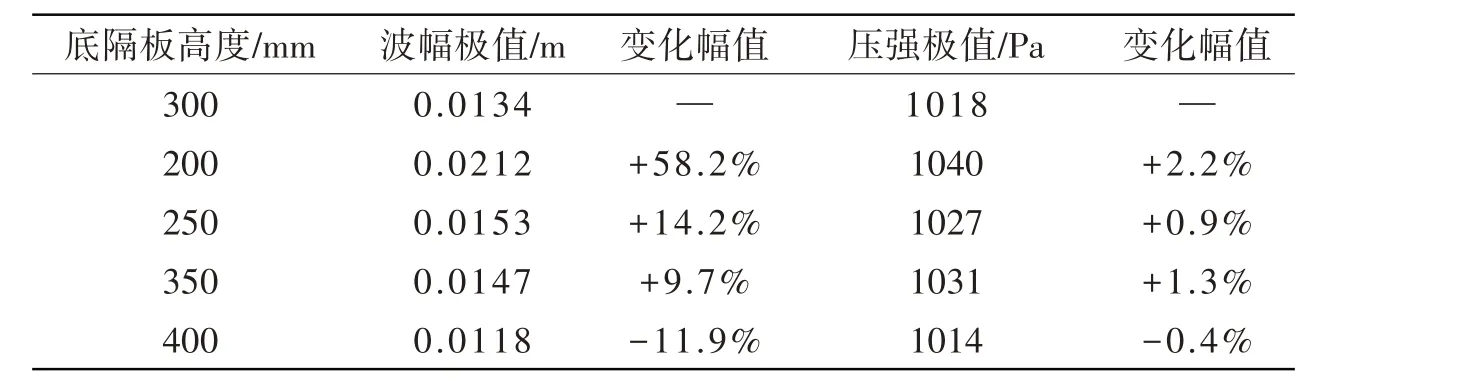
表3 工况一（激励频率6.577 rad/s）Tab.3 Case 1(Excitation frequency 6.577 rad/s)

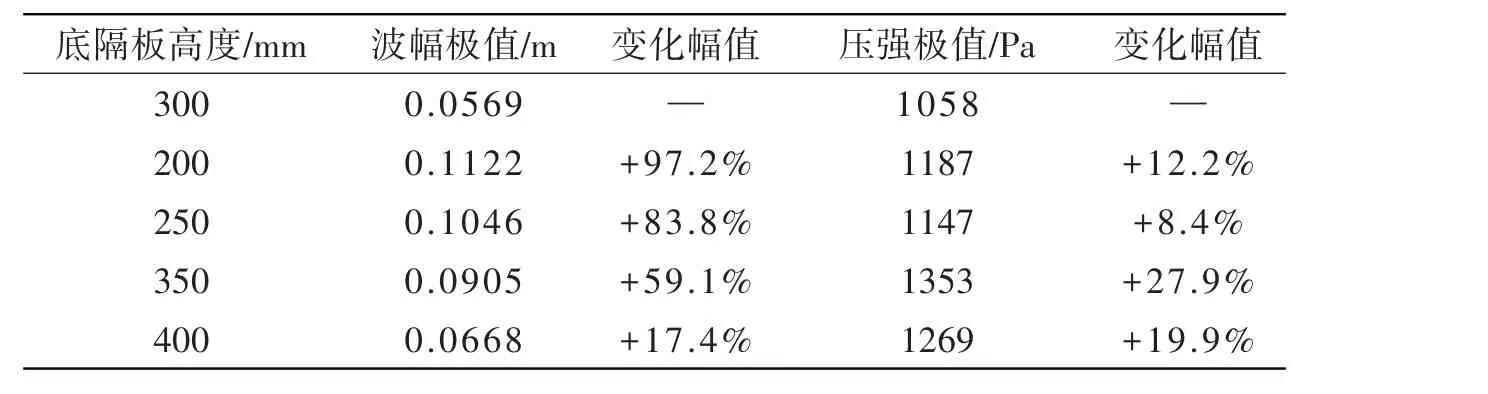
表4 工况二（激励频率4.251 rad/s）Tab.4 Case 2(Excitation frequency 4.251 rad/s)

4 结 论

本文在传统T 型隔板的基础之上，提出了一种新型的DBA 隔板结构。然后基于STAR-CCM+软件，模拟分析了不同外界激励条件下，几种典型转角和尺寸的DBA 隔板对液舱的制荡效果，探讨其对晃荡过程中的液面升高极值、冲击压强大小、速度矢量幅值以及流动状态所产生的作用和影响，得到了以下结论：

（1）当液舱内DBA 隔板转角较小时，隔板不会明显改变液舱的固有频率；当DBA 隔板转角较大时，由于翼缘隔板的遮蔽效应，液舱固有频率会在角度为60°～75°之间时发生突变，且处在一个较高的频率范围之内。

（2）当液舱受到不同频率的水平外界激励时，DBA 新型隔板能够有效地抑制舱内液体的晃荡，使得波幅极值大幅度降低，最佳制荡效果的DBA 隔板结构形式为底部隔板与翼缘隔板等长且转角θ为60°。

（3）最危险载液率条件下，液舱发生受迫运动时，DBA 隔板主要通过诱导生成的漩涡来有效地消耗掉液体晃荡时其激励频率附近的谐波能量，从而减小水质点的运动速度，达到抑制晃荡的目的。