压缩载荷下不同微观结构浮力材料力学特性研究

高 博，陈章兰，孙承猛，王景泽，崔维成

（1.集美大学轮机工程学院，福建厦门 361021；2.山东交通学院船舶与港口工程学院，山东威海 264209；3.西湖大学工学院，浙江省海岸带环境与资源研究重点实验室，杭州 310024）

0 引 言

微珠复合泡沫材料是一种常见的固体浮力材料，主要由空心玻璃微珠、环氧树脂组成，具有强度高、密度低、吸水率低、可机加工等优异的特性，是深海无人/载人潜水器的一种重要材料[1]。在我国“十三五”期间开展全海深无人/载人潜水器研制时，发现国内外所有的供应商中没有一家可以提供满足潜水器设计规范要求的强度级别的浮力材料，这是因为当前玻璃微珠/环氧树脂型的固体浮力材料基本上已经优化到了强度极限，不太可能指望生产厂家在短期内能够生产出满足规范强度要求的新产品[2]。这就要求在全海深无人/载人潜水器中超规范使用现有的浮力材料。对浮力材料的有效弹性模量、破坏准则等力学特性更深入的了解，将为浮力材料如何超规范使用，如安全措施标准选择，提供一定的理论支撑。对微珠复合泡沫材料力学行为相关的研究，主要涉及模量和强度的理论和数值仿真预测、以及试验研究。例如：卢子兴利用三相、四相、五相球模型预测了浮力材料的有效弹性模量[3-8]；陈鹿等[9]利用ANSYS 软件从微观角度分析固体浮力材料的弹性模量；Marur 等[10]采用理论和数值方法研究了浮力材料的宏观弹性行为；Yu 等[11]利用有限元软件，从微观结构出发，预测浮力材料的弹性力学行为；Bardella[12-16]通过建立包含多微珠三维有限元模型，分析和研究浮力材料的破坏准则，以及涂层对浮力材料性能的影响。理论计算结果通常表示材料的平均水平，不能较好体现局部的不同；有限元模型通常对浮力材料细观结构进行理想化，如假设微珠直径（外径）一样，均匀分布在基体中，材料各向同性[17]。研究者对于含有不同微珠外径、壁厚等浮力材料强度预测还较少报道。为了更好地了解由不同外径、壁厚组成浮力材料的应力分布，以及对于微珠破坏的影响，提出考虑微珠大小、壁厚和体积分数等因素后材料有效弹性模量的预测公式、微珠弹性应变能等。本文采用ANSYS 软件，建立由多种微珠外径、壁厚、体积分数组合而成单胞有限元模型，分析压缩载荷下浮力材料有效弹性模量的影响因素，相邻微珠外径不同、壁厚不同等的应力分布，探讨浮力材料的强度预测问题，同时通过试验验证破坏准则。

1 弹性模量计算

基于微分等效介质理论，浮力材料中均匀加入等体积的空心玻璃微珠，可建立复合材料的有效模量与基体有效模量、玻璃微珠有效模量及其体积含量之间的微分关系，得到以下微分方程式[18]：

式中，K、μ分别为浮力材料的体积模量和剪切模量，K2,、μ2分别表示空心玻璃微珠的体积模量和剪切模量，F为玻璃微珠的体积分数。

固体浮力材料在静水压力作用下，可简化成三相球模型的自洽模型，三相球模型如图1 所示，微珠内部为气相，微珠壁材部分为增强相和外侧基体相。可得到玻璃微珠的等效体积模量[3]，以及空心玻璃微珠的等效剪切模量分别为

式中，Kg、μg分别表示玻璃微珠壁材的体积模量和剪切模量分别为空心玻璃微珠内外径，内外径之比η=ri/ro，如图2所示。

图1 三相球模型（自洽模型）[7]Fig.1 Three-phase spherical model(self-consistent model)[7]

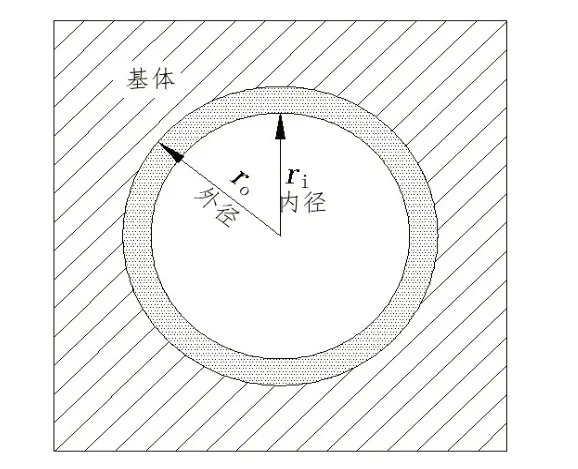
图2 浮力材料二维示意图Fig.2 Two-dimensional schematic diagram of buoyancy materials

在求解浮力材料的有效体积模型和剪切模量后，可利用公式（5）的弹性常数间的相互关系，来确定浮力材料的有效弹性模量，以及弹性模量随空心微珠体积分数的变化趋势。

从公式（1）～（5）可发现浮力材料的等效弹性模量与微珠的体积模量和剪切模量成正相关，而微珠体积模量和剪切模量与微珠的内外径之比有关。

以上方法是基于基体中加入的微珠外径和壁厚都一样。浮力材料通常由空心玻璃微珠、气孔及基体三相组成，且制造过程中存在微珠破裂或者微珠与基体脱粘等缺陷。针对脱粘微珠和破裂微珠等缺陷部位可简化成气孔[19]。同一批次的玻璃微珠大小和壁厚通常存在不同。因此，计算浮力材料弹性模量时，应充分考虑气孔、微珠壁厚等因素。为解决浮力材料有效弹性模量问题，可采用多次单相夹杂的思路。假设存在两种壁厚空心玻璃微珠（即第一类壁厚微珠和第二类壁厚微珠），夹杂过程为：第一步将第一类微珠与基体组合，第二步以第一步组合成的浮力材料作为新的“基体”，将第二类HGM填充在新基体，第三步以第二步组合成的浮力材料再次作为“基体”将气孔作为填充进行添加。

在基体中添加微量微珠或气孔后，材料弹性模型的变化可通过微分形式表示，即dE与dφ关系式，考虑到微珠体积分数增大后，颗粒之间的相互作用就会变得不可忽略。经文献[20-23]证明，将dφ用dφ（1-φ/φm）表示能较好地解决以上问题。多次夹杂可通过下列微分方程解释：

式中，φ1、φ2、...φN为添加微珠的体积分数，φm为基体体积分数。通过上式理论上可求解浮力材料的弹性模量，但较难确定不同外径和壁厚的微珠的比例，第一次组合后，添加气孔公式预测较好[19]，但是对于后续多次添加不同壁厚、粒径的微珠，结果有待验证。从上式中可发现，微珠内外径之比η是影响浮力材料弹性模量的主要因素，计算过程中针对微珠微观结构可做一定等效简化。假设所有微珠外径一样，此时不同微观结构主要体现在微珠的壁厚（η不同）。此时在计算时可引入平均内外径之比ηˉ，平均内外径之比可通过微珠体积分数、微珠壁材密度和微珠质量求得。每一个微珠的内外径之比与平均值差可采用Δηi表示，即

文献[24]给出了基于平均壁厚和体积分数的二阶微分修正参考，并与试验结果相吻合。

由于微珠尺寸小，工程中想要准确知道浮力材料不同外径和壁厚的微珠数量困难较大，可提出如下简化过程：以生产批次微珠内外径平均值为基准，第一次，基于平均差-- --Δηi，将微珠分为高于和低于平均值两类，同时取各自类别中的平均值；第二次，以第一次的两类微珠的新平均值为基准，再次将微珠分为新的高于和低于两类。当Δηi为负数时，且数值越小，起到的增强效果越小，甚至对浮力材料弹性模量有减弱作用。

2 压缩强度及破坏准则分析

2.1 压缩强度经验公式

Turcsanyi[25]对抗压强度提出了一个半经验的公式：

式中，A为常数，与填料形状有关，对于球形微珠，A=2.5。

Nicolais和Narkis[26]，Ahmed和Jones[27]在考虑玻璃微珠的孔隙影响的基础上提出：

式中，σcu为浮力材料极限强度应力，σmu为基体极限强度应力，Vs、Ve和Vg分别为玻璃微珠、基体和孔隙体积含量。

从以上公式可发现，针对强度的预测公式主要考虑基体极限强度应力与各相体积含量之间的关系，并没有考虑浮力材料的微观结构对压缩强度和应力分布的影响。

2.2 破坏准则

通过阅读已发表的文献可发现，压缩载荷作用下，浮力材料的破坏模式主要有：包括不同加载方向在内的平面分裂的脆性破坏[28-29]、准脆性剪切破坏[30-31]、垂直于加载方向发生的局部“弱层”破坏[32]、在均匀体积载荷或其他普遍压缩的载荷条件下微球的大规模断裂、没有宏观断裂和大的非弹性变形[33]。

格里菲里提出理想晶体的理论断裂强度公式为

式中，γ表示单位面积上的断裂表面能，a为平衡晶格常数，σth为广义破坏强度。通过上式说明材料的破坏强度与γ平方根成正比，如果为球形材料，受到剪切破坏时，可以得出：

微珠为中空球，可根据比面积

根据文献[34]，

式中，K与材料的弹性模量（Em，Eg）、泊松比（μm，μg）、微珠中空度Vh和体积占比Vg等相关，k为比例常数，pth为破坏压力。

从上面公式中可以看出，当微珠的体积分数和内外径之比相同时，则K值一样，破坏压力与微珠半径平方根成反比，随着压力增大半径较大的微珠将先发生破坏。实际浮力材料中玻璃微珠的大小和壁厚不统一，k和K值通常是不一样的，两个变量的值对于材料的破坏起源预测增加了难度和不确定性，因此，计算过程中为减少变量，可以结合能量入手，考虑微珠的弹性应变能。

式中，σij，εij分别为空间应力和应变值，S为微珠表面积，V为微珠体积。

文献[13]提出了破坏应力和破坏弹性应变能临界值关系式，载荷作用下，应变能超过临界时微珠将发生破坏，

公式（19）并未考虑微珠大小对破坏的影响，实际浮力材料中，存在不同大小的微珠，不同大小的微珠在浮力材料中各自占的体积分数也不同，令

若式（19）中p0为微珠的破坏压力，则p0=pth，综合公式（17）、（19）和（20），可得出U0与微珠外径的关系：

微珠的大小对弹性应变能存在一定的影响，但不能简单地认为是反比关系，弹性应变能需要综合考虑微珠壁厚、体积分数和半径的影响。

3 数值计算

材料在弹性变形阶段，其应力和应变成正比例关系（即符合胡克定律），其比例系数称为弹性模量。数值计算基于ANSYS 有限元分析软件开展，施加位移载荷，位移大小为基体边长1/100。通过软件可提取载荷加载面的支反力，端面支反力之和除以表面积为端面的应力。

玻璃微珠/环氧树脂固体浮力材料的微珠壁厚、微珠半径、微珠体积分数对材料的力学行为有较大影响，研究固体浮力材料细观结构在位移载荷作用下的杨氏模量、压缩强度，对实际生产具有一定的指导意义。本文采用的基本假设是：微珠与树脂基体完好粘结，即相当于刚性连接；微珠均匀分布于树脂基体中；浮力材料中不存在杂质和气泡；浮力材料力学性能均为各向同性。

3.1 有限元模型

（1）模型概述

基于上述假设，建立了浮力材料的体心立方单胞模型，单胞模型由两个玻璃微珠和树脂基体组成，基于对称原理和减少运算量原则，将模型简化为1/8单胞模型，如图3（b）所示。

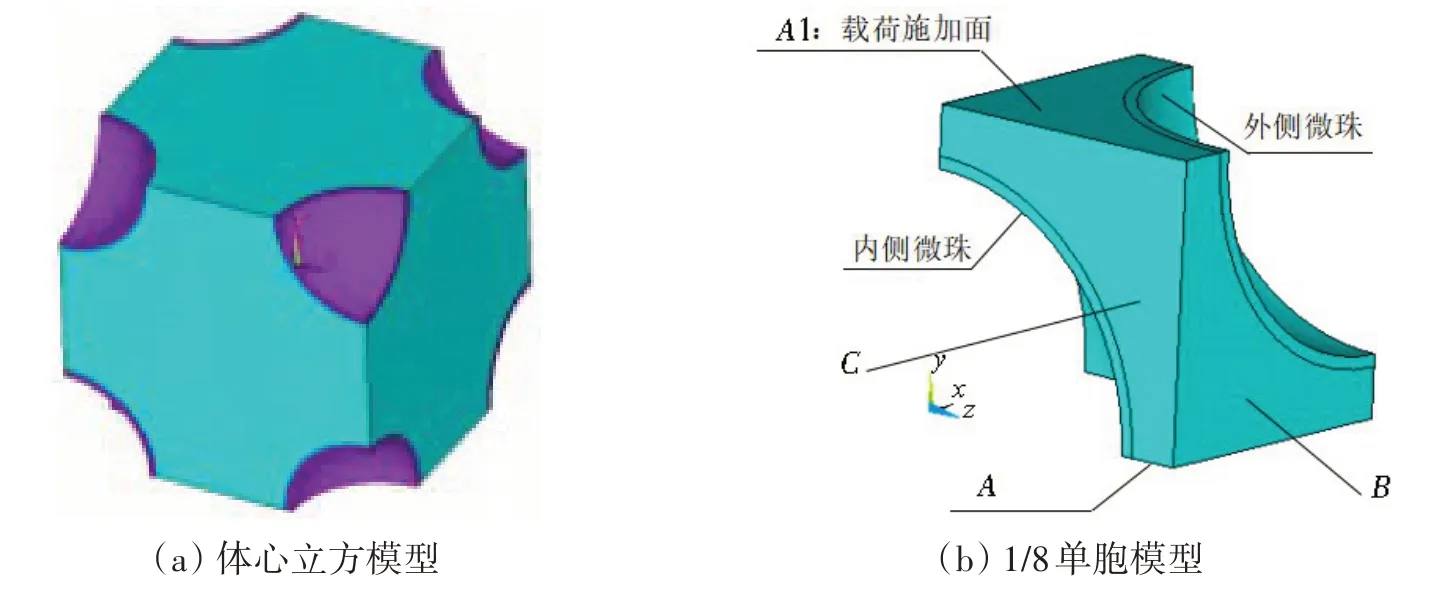
图3 浮力材料单胞有限元模型Fig.3 Finite element model of buoyancy material

（2）网格划分

模型单元选择三维10 节点实体单元Solid187，材料参数如表1 所示，采用自由网格划分，划分网格后模型如图4所示。

（3）边界条件

分析弹性模量时的边界条件：对A面施加固定约束，A1面为施加载荷面，施加位移载荷，B面、C面的法向位移为零[35]，如图5所示。

分析压缩强度时的边界条件：A1面施加40 MPa载荷，A面、B面、C面施加位移约束，设置三个面的法向位移为零[36]。

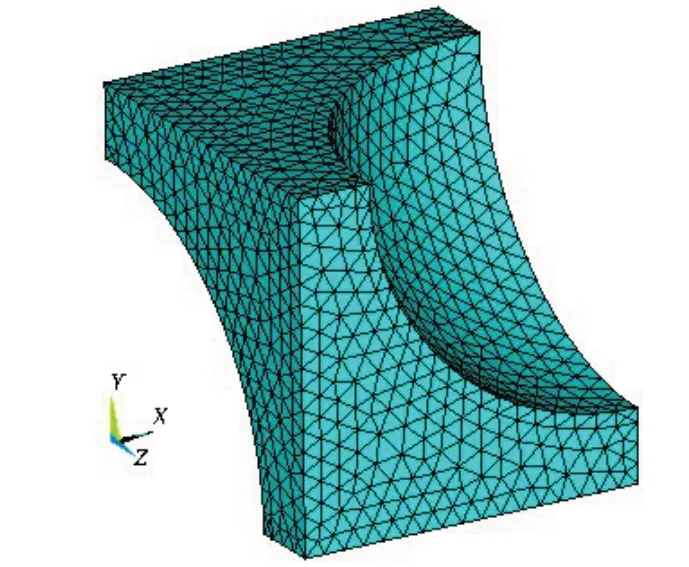
图4 网格划分图Fig.4 Meshing

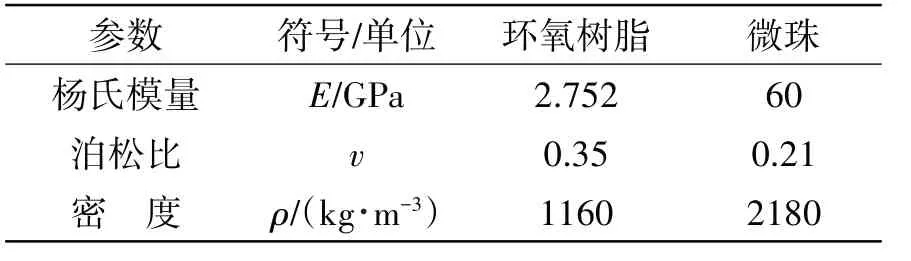
表1 材料参数Tab.1 Material properties

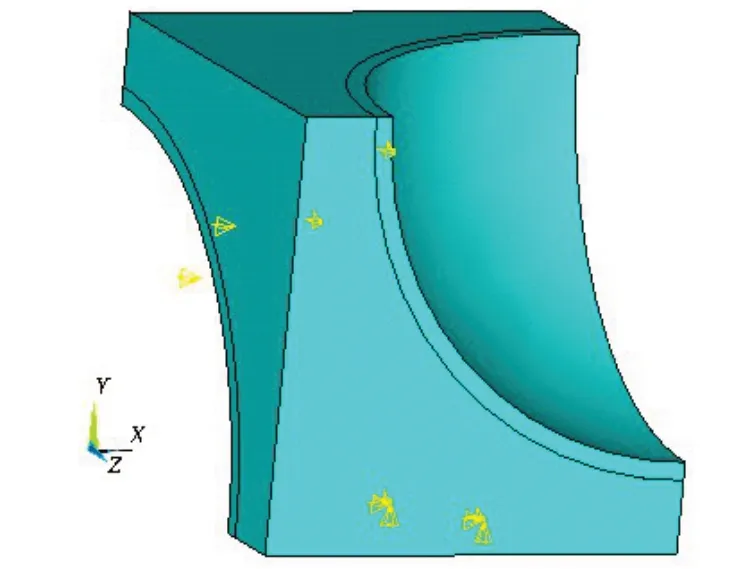
图5 分析弹性模量时约束情况Fig.5 Constraints when analyzing elastic modulus

3.2 计算工况

本文建立了三维单胞有限元模型，Hobaica 和Cook[37]的测试结果表明，当微珠体积占比超过67%时，由于浮力材料中气泡和污染物的增加以及微珠与基体界面的完整性变差，浮力材料的吸水率显著增加，一般认为67%为微珠体积占比的上限。基于微珠的体积分数设计的20类工况（表2），分别对微珠体积分数为10%、20%、30%、40%、50%和60%进行计算和分析，不同微珠内部结构模型的平面投影如图6所示。

我们对不同微观结构的浮力材料弹性模量和压缩强度情况进行了分析，主要分析的工况如下：

（1）两个微珠外径、壁厚一致，改变微珠的体积分数，同时改变两个微珠外径，分析微珠体积分数、微珠大小与浮力材料的弹性模量的关系、基体和微珠应力分布情况；

（2）两个微珠外径一致，固定为20µm，改变微珠体积分数、微珠的壁厚，分析壁厚与材料的弹性模量的关系、微珠应力分布情况，验证破坏准则；

（3）两个微珠半径不一致，体积分数相同和不同时，微珠壁厚不同，分析基体和微珠应力分布，以及加载方向对材料的内部应力的影响，验证破坏准则。本文计算工况如表2所示。

表2 计算工况Tab.2 Calculation conditions

图6 不同微观结构模型示意图Fig.6 Diagram of different microstructure models

4 结果与讨论

4.1 试验结果

选用Engineered Syntactic Systems（ESS）公司HZ-42 浮力材料，材料尺寸为610 mm×305 mm×100 mm，进行静水压试验，按2～3 MPa/min的速度均匀加压至试验压力值165 MPa，并保压2小时。试验后取材料部分区域放大250 倍SEM 图如图7 所示。图7 中可发现破坏的微珠存在半径较大又存在较小的微珠，说明微珠的破坏强度与微珠大小不是简单的反比关系，微珠的破坏需要同时考虑微珠的壁厚和大小等因素；从图中还发现微珠的破坏通常在赤道位置开始。

4.2 微珠大小和体积分数对浮力材料弹性模量的影响

根据胡克定律，单轴应力状态下的应力应变关系如下：

式中，σ为应力，ε为应变，d为加载位移载荷，l为三维模型基体边长，S为施加载荷面表面积。

环氧树脂基体中加入的空心玻璃微珠组成浮力材料，当空心玻璃微珠有效弹性模量大于基体弹性模量时，微珠属于材料的颗粒增强元素，此时加入越多，越有利于提高浮力材料的弹性模量，因此玻璃微珠的体积分数和壁厚对于浮力材料的弹性模量具有重要影响。我们设计了A1-A6 工况（详见表2），对单胞模型进行有限元分析。发现浮力材料有效弹性模量与微珠体积分数成正相关，但是随着内外径之比的变大（即壁厚变薄），有效弹性模量的变化随微珠体积分数的变化趋于平缓，如图8 所示，壁厚越薄玻璃微珠的有效弹性模量越低，可以预测当玻璃微珠壁厚减小至某一值时，浮力材料的有效弹性模量将等于基体的弹性模量，规律与文献[9]的一致；微珠壁厚继续变薄，浮力材料的有效弹性模量将低于基体的弹性模量，此时，加入微珠将降低浮力材料的强度。

为研究微珠大小对浮力材料弹性模量的影响，我们设计了A7-A10工况（见表2）进行单胞模型有限元分析，发现当微珠体积分数一样时，A7-A10 工况浮力材料的有效弹性模量值与A2 工况的一样。说明，当浮力材料中添加微珠的体积分数一样、内外径之比一样，且一种浮力材料中的微珠大小相同（不同种浮力材料中微珠彼此间大小不一样）时，浮力材料的有效弹性模量值相同，此时，不同材料间的有效弹性模量与微珠外径大小无关。

图7 静水压力下微珠破坏250倍SEM图Fig.7 Crack section of solid buoyancy material under hydrostatic pressure

图8 不同体积分数材料的有效弹性模量Fig.8 Effective elastic modulus of materials with different volume fractions

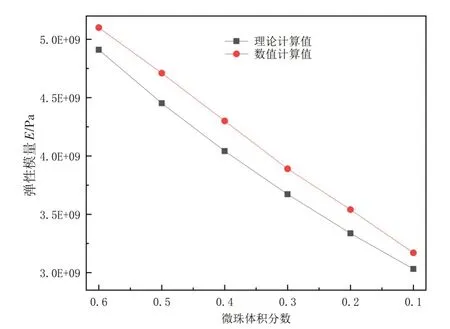
图9 理论与数值计算所得弹性模量随体积分数变化Fig.9 Theoretical and numerical calculation of elastic modulus with different volume fractions

基于表2中A1工况和表1数据，利用式（3）、式（4）求得玻璃微珠的体积模量和剪切模量后并代入式（1）和式（2）求出浮力材料的K、µ，最后将K、µ代入式（5）可解出浮力材料的有效弹性模量，结果见表3，理论计算与数值计算结果随体积分数变化情况如图9 所示。从计算结果可发现：两种情况算出的结果随体积的变化都接近线性变化，且两条线的斜率差值较小；数值计算值略大于理论计算值，差别在3%～6%区间内，由此可见，两种方法用于计算浮力材料的有效弹性模量是合理的。

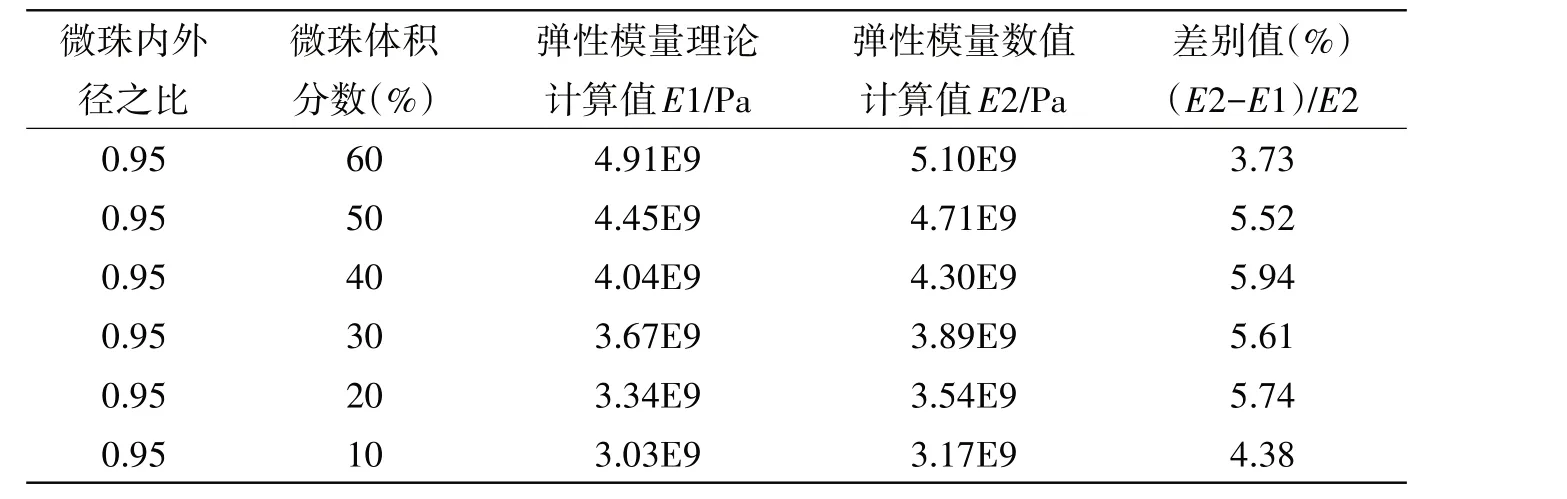
表3 有效弹性模量理论计算与数值计算比较Tab.3 Comparison between theoretical and numerical calculations of effective elastic modulus

当浮力材料中出现微珠破损、气泡、脱粘等缺陷时，可以将缺陷简化成气孔，基于多次夹杂原理，通过式（6）和式（7）可计算材料的有效弹性模量。基于表2中A1部分工况，材料中存在缺陷时，不同缺陷体积分数的计算结果见表4。

表4 浮力材料存在缺陷后有效弹性模量理论计算与数值计算比较Tab.4 Comparison between theoretical and numerical calculations of effective elastic modulus for buoyancy material with defects

通过比较E3与E1差值比例，发现将缺陷简化成气孔后，由于气孔的体积模量和剪切模量都为0，所以当缺陷所占体积分数一样时，微珠的体积分数对于浮力材料的弹性模量下降水平影响很小。

通过对A2和A4工况进行分析，当浮力材料体积分数一样时，浮力材料的有效弹性模量随微珠厚度的增大而增大，与体积分数成正相关，浮力材料的有效弹性模量变化趋势与微分法计算结果一致。在施加相同压力载荷时，当较薄微珠远离载荷加载面，最大应力值出现在较薄微珠上，且应力值要远大于较薄微珠在载荷施加面时的；较薄微珠在载荷施加面时，最大应力随着较薄微珠壁厚变薄，最大应力值变大。这说明随着载荷的增加，较薄的微珠将先到达破坏应力的临界值，即先破坏，验证了2.2节中的破坏准则，与文献[12]的结果一致。

4.3 两个微珠内外径之比一样时，微珠大小对于浮力材料压缩强度的影响

浮力材料中，不同粒径玻璃微珠，不仅对于微珠和基体粘结性有影响，而且对浮力材料的应力分布情况也存在影响，在压缩载荷下，微珠和基体的最大应力位置及趋势将影响材料的破坏强度。本文设计B1-B10 计算工况，选取其中两个内外径之比一样的微珠，包括：0.9、0.92、0.94、0.95 和0.96，分析加载方向和粒径对浮力材料压缩强度的影响，研究浮力材料的破坏。体积分数较大时，材料的破坏将以微珠破坏为主[28-33]，本文重点关注微珠的失效，以微珠的失效强度来反应浮力材料的强度，分析过程中微珠的应力值为微珠壁材的强度。

当微珠体积分数较大时，最大应力出现在内侧微珠，且应力值明显高于外侧微珠，说明材料中存在不同大小的微珠时，最大应力与载荷的施加位置有关；随着微珠内外径之比变大，材料的最大应力值也变大，说明材料的强度与微珠壁厚有关。

外径较小微珠在内侧时，随着两个微珠外径的接近，最大应力的值逐渐变大，两个微珠大小一样时，最大应力值最大。外径较大微珠在内侧时，此时最大应力值比外径较小微珠在内侧时的值大，两个微珠外径相同时，最大应力的值最小。

通过分析，最大应力位置通常出现在内侧微珠（远离加载面）的赤道，如图10 所示的内侧微珠外径不同的应力云图，说明微珠破坏从赤道位置开始破坏，与图7中显示的结果一样。图11显示的是微珠体积分数为50%，外径为15µm 和10µm 的两个微珠在不同位置随内外径之比变化的最大应力值，从图中可知较大微珠在内部时，最大应力值较大。因此，当微珠内外径之比一样时，相同载荷下，外径较大的微珠先到达破坏临界值，将先破坏，验证了2.2 节中的破坏准则，即微珠内外径之比一样，微珠的破坏速度与微珠的外径成反比。

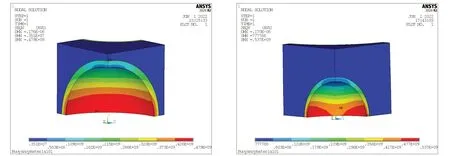
图10 浮力材料应力云图Fig.10 Stress clouds of buoyancy material

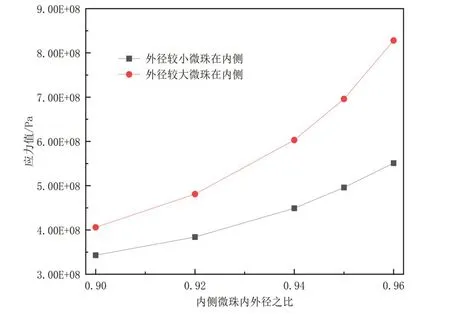
图11 微珠外径不同时浮力材料最大应力值随内外径之比变化曲线Fig.11 Variation of maximum stress value of buoyancy materials with η at different outer diameters of HGMs

4.4 两个微珠内外径之比不一样时，微珠大小对于浮力材料压缩强度的影响

本文设计B1～B10 计算工况，选取微珠内外径之比分别为0.9、0.92、0.94、0.95 和0.96，且模型中两个微珠的内外径之比彼此不一样，对浮力材料的压缩强度进行分析。

通过分析发现，当微珠体积分数较大时，最大应力出现在内侧微珠赤道位置的内表面。

（1）外径较小微珠在内侧：当微珠体积分数较大时，最大应力出现在内侧微珠赤道位置的内表面；当外侧微珠内外径之比不变时，随着内侧微珠壁厚变薄，微珠的最大应力值变大；当内侧微珠壁厚不变，改变外侧微珠壁厚时，最大应力值变化幅度很小。

（2）外径大的微珠在内部：当微珠体积分数较大时，如一个微珠壁厚保持不变，则另一个微珠的最大应力值会随着微珠壁厚的变薄而变大，内侧微珠的最大应力值随两个微珠的大小之比（外侧微珠外径/内侧微珠外径）变小而变大。

通过分析，最大应力位置出现在内部微珠赤道位置，外侧微珠壁厚不变而改变内侧微珠壁厚（减小壁厚）时，比仅改变外侧微珠壁厚（减小壁厚）时最大应力值更大；外径较大微珠在内侧最大应力值最大，说明微珠的破坏与外径和施加方向相关，验证了破坏准则。通过比较两个不同大小微珠在内侧时的最大应力可以发现，外径小的微珠壁厚比较大微珠壁厚薄时，小微珠上的最大应力也会大于较大微珠的，如图12 所示，外侧微珠内外径之比为0.9，内侧微珠内外径之比分别为0.9、0.92、0.94、0.95 和0.96，从图中可看出小微珠在内侧时且内外径之比为0.95 时最大应力值大于大微珠在内侧内外径为0.92 时的值，如果材料中存在上述两种微珠，在相同载荷下，小微珠将先发生破坏。与图7中显示的一致，说明壁厚和半径对微珠的破坏都有影响。

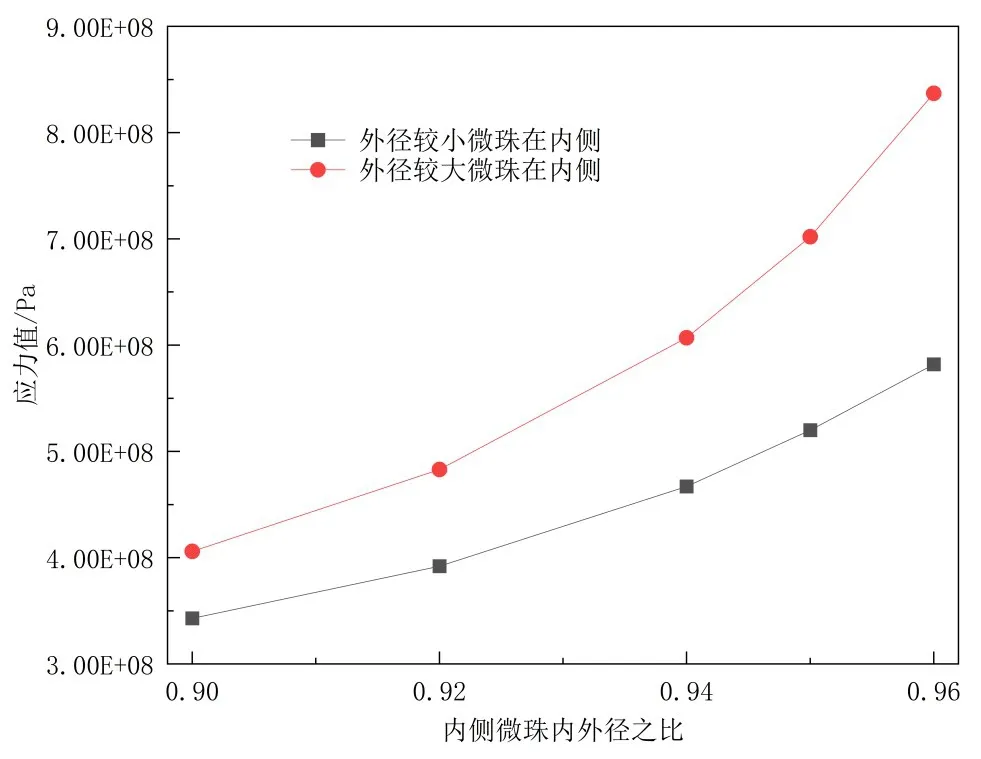
图12 内侧微珠内外径、壁厚不同时最大应力值Fig.12 Maximum stress values of inner HGM with different outer diameters and wall thicknesses

5 结 论

本文对压缩载荷下不同微观结构浮力材料力学特性进行了研究，给出了含不同规格微珠的浮力材料有效弹性模量微分计算公式，分析了微珠破坏准则，利用ANSYS 软件构建的三维细观单胞模型对浮力材料进行了力学性能有限元分析，通过实验和有限元数值分析手段对破坏准则进行了验证，得到如下结论：

（1）当浮力材料中所有玻璃微珠的外径大小一样、壁厚一样时，浮力材料有效弹性模量仅与微珠体积分数有关，而与外径大小无关；当内外径之比小于某个值时，浮力材料的有效弹性模量与微珠体积分数成正相关，此时玻璃微珠对浮力材料的刚度起到增强作用，但当微珠内外径之比较大时，浮力材料的有效弹性模量的变化会随微珠体积分数的变化趋于平缓。

（2）微珠的破坏可以从弹性应变能角度分析，破坏强度与微珠的壁厚和大小都存在关系，微珠的破坏通常从赤道处开始。通过有限元分析，当微珠大小和体积分数不同时，最大应力通常出现在远离加载面的微珠赤道位置，说明微珠的破坏与加载方向存在一定关系。

（3）当浮力材料中的微珠内外径之比相同、微珠大小不同时，此时较大微珠将首先发生破坏，微珠的破坏速度与微珠的外径成反比；浮力材料中的微珠外径相同、内外径之比不同时，较薄微珠将先发生破坏。

（4）微珠内外径之比和微珠大小均不一样时，微珠的壁厚和大小将对微珠的应力产生不同程度的影响，两者的影响敏感度需要进一步研究。