基于迁移学习的多源波浪载荷融合方法研究

陈 帅，蒋彩霞，王子渊，张 凡，王艺陶

（1.中国船舶科学研究中心，江苏无锡 214082；2.深海技术科学太湖实验室，江苏无锡 214082）

0 引 言

船舶波浪载荷，特别是恶劣海况下的强非线性波浪载荷是海洋结构物安全可靠运行的“潜在杀手”。现如今，对于如何准确快速评估高海况下作用于船舶结构上的外载荷已成为船舶结构安全性与可靠性方向的研究热点。为研究高海况下船舶结构响应，使得设计者获得船舶总纵应力极值分布，研究人员提出了多种非线性波浪载荷预报方法，如三维时域非线性水弹性理论[1-2]、CFD-FEA 双向耦合方法[3-4]、极端波浪载荷预测[5-6]和混合时域边界元法[7]等，这些方法的准确性主要还是通过模型试验[8]对比来验证。波浪载荷试验在现代船舶结构设计中发挥着重要的作用，通常研究者们把数值计算方法作为波浪载荷试验的重要补充，但是存在极端条件下计算精度不足的问题。船模试验和数值计算的波浪载荷数据有效融合，不仅能降低波浪载荷计算和试验成本，还可以提高波浪载荷的预测精度。

受客观或主观因素的制约，模型试验的工况往往十分有限，如何将小样本的试验数据与理论计算结果进行有效融合，对于波浪载荷快速有效预报意义重大，因此，也出现了一些数理方法和机器学习等新型方法对波浪载荷进行智能预报的探索。迁移学习[9]旨在通过迁移不同但相关的源域蕴含的知识来提高目标学习器在目标域上的表现，可以减少构建目标学习器对大量目标域数据的依赖，非常适用于船模试验和数值计算的载荷数据融合应用场景。Li 等[11]提出了一种多源压力融合模型，该模型基于大量数值计算数据和少量风洞试验数据融合进行压力分布预测。Zhao等[12]提出了跨领域的航空发动机故障诊断方法，该方法基于两阶段迁移学习只需少量的目标域数据就可以获得很高的诊断准确率。迁移学习[10]是机器学习中解决训练数据不足的基本问题的重要工具，它通过放宽训练数据和测试数据必须是独立同分布的假设，将知识从源域转移到目标域。这将对许多由于训练数据不足而难以改进的领域产生巨大的积极影响。迁移学习还在自然语言处理[13]、医学成像[14]和图像分类[15]等领域被广泛应用。

通常在船舶初步设计中，进行大量的模型试验是昂贵的、耗时的，甚至是不切实际的。迁移学习是经验概括的结果，可以实现从理论计算域到模型试验域的知识转移。因此本文在传统切片理论基础上结合机器学习方法实现了波浪载荷的智能预报。为了泛化模型试验，以数值计算波频数据作为源域一、规则波模型试验波频数据作为源域二、不规则波模型试验合成数据（波频与砰击叠加）为目标域，基于迁移学习建立多源波浪载荷融合方法，对不规则波工况下的波浪载荷预测进行二次修正。该方法使得船舶设计者更方便和高效地计算船舶在不同航速、海浪周期、波高及航向角下任意剖面的外载荷响应，对船舶结构分析与设计意义重大。

1 低频波浪载荷智能预报（LFWLIP）方法

1.1 低频波浪载荷智能预报方法

本文结合试验设计方法、数据标准化处理方法、线性切片理论和深度神经网络[16]（deep neural networks，DNN）建立了低频波浪载荷智能预报（low frequency wave load intelligent prediction，LFWLIP）方法，如图1。图中采用的波浪载荷程序（LILOAD.exe）为中国船舶科学研究中心自主开发的线性波浪载荷计算程序，后文与试验数据对比验证了该程序的合理与准确性。本文通过计算和分析，建立适用于LFWLIP的数据处理、试验设计和机器学习等分析方法，实现线性波浪载荷高精度和快速计算。

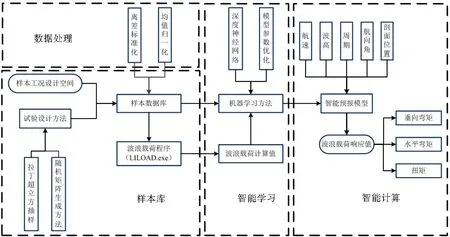
图1 LFWLIP方法Fig.1 LFWLIP method

1.2 模型评估指标

智能预报模型预测结果与波浪载荷计算值的均方误差Mse作为训练过程中的评估指标，均方误差也称为收敛过程中的Loss值，计算公式为

式中，n为样本工况数，yi、y̑i为第i个工况的预测值和计算值。

1.3 模型验证指标

为了评估智能预报模型的拟合程度，本文选择均方根误差Rmse和拟合优度统计量R2作为评价指标，公式为

式中，yˉ为计算值的平均值。

2 试验设计与数据处理方法

试验设计（design of experiments）方法是数理统计学的一个分支，它提供了合理而有效的获得信息数据的方法，要实现波浪载荷的智能预报，如何设计样本工况将影响模型构建的速度与精度。本章主要分析波浪载荷数值计算数据集输入参数和输出参数之间的关系和趋势，在构建智能预报模型的同时，提高样本工况设计的稳健性。

2.1 多源波浪载荷数据

以不规则波工况下的波浪载荷短期预报为目标，多源波浪载荷数据包括数值计算数据（低频）、模型试验规则波中的传递函数（低频）和模型试验不规则波工况数据（合成）。波浪载荷短期预报以规则波中的波浪载荷响应为基础，通过理论计算，确定船舶在给定时间运行于实际海况中的波浪载荷变化特性，波浪载荷短期预报[17]有义值为

式中：Sζ(ω,H,T,θ)是ISSC 双参数谱；H(ω,V,TZ,β+θ)是系统传递函数的模，其值为单位规则波下的载荷响应幅值；ω是波浪圆频率；V是航速；θ是组合波与主浪向的夹角；H是有义波高；T是波浪的特征周期；β为航向角。

以某船为对象，数值计算数据源于中国船舶科学研究中心自主开发的线性波浪载荷计算程序，本文称为低精度数据集。模型试验在中国船舶科学研究中心耐波性水池开展，包括规则波模型试验和不规则波模型试验。图2为单位波高下某船低频波浪垂向弯矩传递函数，以工况B01航速10 kn、顶浪180°和工况B02航速18 kn、斜浪150°为例，给出了10站处数值计算与模型试验数据的对比，可以看出规则波中数值计算与模型试验的传递函数较为吻合。

图2 单位波高下低频波浪垂向弯矩传递函数Fig.2 Low frequency wave vertical moment transfer function under unit wave

对于不规则波模型试验（合成），高频为砰击颤振等非线性成分，本文称为高精度数据集。图3为不规则波工况下的波浪垂向弯矩计算值与试验值低频成分对比，从图中可以看出本文程序的低频波浪载荷短期预报结果与试验值较为吻合。对于高频成分，表1 给出了部分不规则波工况模型试验高频与合成的比值，从表中可以看出航速与波高越大，高频成分占比越大，其砰击、上浪等现象会更明显，总体而言高频成分占比10%～60%。

图3 不规则波工况下的低频波浪垂向弯矩计算与试验对比Fig.3 Calculation and experimental comparison of low frequency wave vertical bending moment in irregular wave condition

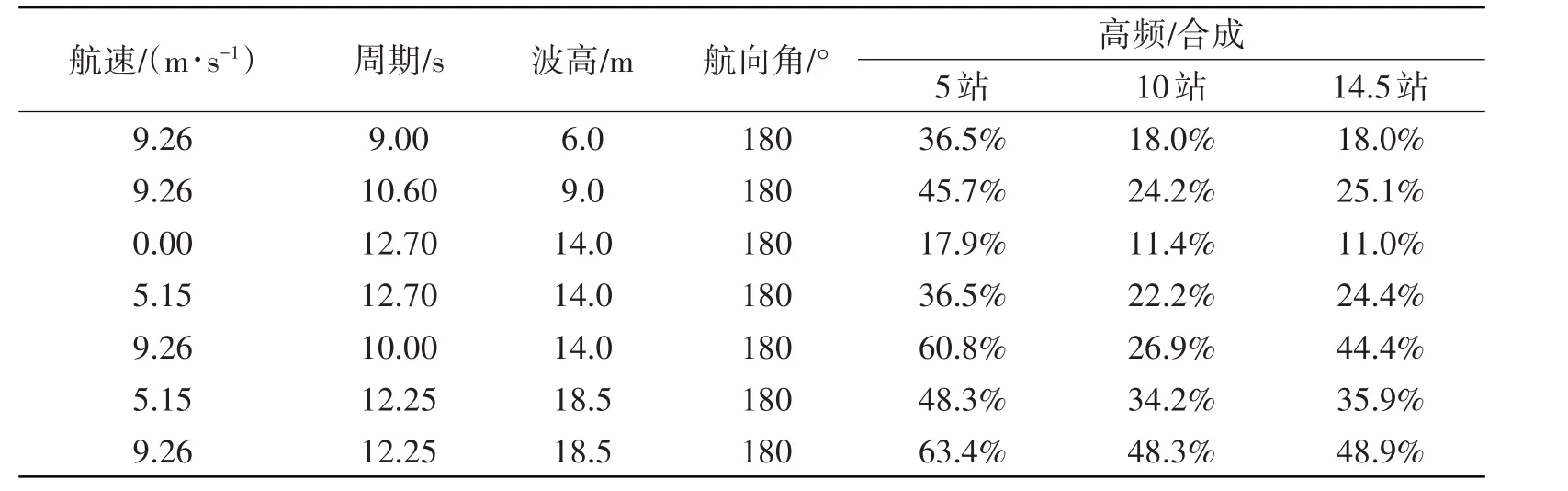
表1 部分不规则波工况模型试验高频成分Tab.1 Part of the model test high-frequency components under irregular wave working condition

2.2 拉丁超立方抽样

拉丁超立方抽样[18]（Latin hypercube sampling,LHS）使所有的试验点尽量均匀地分布在设计空间中，它在数据密度和位置方面具有灵活性，还具有非常好的空间填充性和映射性。随机矩阵生成（random matrix generation,RMG）方法，即在样本空间中随机产生n个样本。

为了分析样本数据对预报精度的影响，采用RMG 方法和LHS 试验设计方法生成200～2000 个样本，其中LHS使用pyDOE开源库。图4～5所示为R2和Rmse随样本数n的变化，从图中可以看出，当样本数小于400时，LHS方法明显优于RMG方法，这是由于拉丁超立方抽样具有较好的样本空间填充性和均衡性，但随着样本数的增加，LHS方法并没有太大的优势。当样本数大于1600时，随着RMG方法生成的样本数据会出现严重的冗余现象，样本空间中相同位置生成了大量重复性数据。

图4 R2随样本数n的变化Fig.4 Variation of R2 with sample number

图5 Rmse随样本数n的变化Fig.5 Variation of Rmse with sample number

图6 所示为不同样本数n下验证集计算值与预测值的对比，从图中可以看出，预报模型在值偏大时的预测能力小于值偏小时，与样本数无关。随着样本数的增加，R2增大，值偏大情况下的预测效果也逐渐变好，但RMG 方法还会出现预测值与计算值相差偏大的情况。综上，考虑到计算时间和精度，下文的分析采用LHS方法生成n=1800的样本数据。

图6 不同样本数n下的测试集计算值与预测值相关性分析Fig.6 Correlation analysis between calculated and predicted values of test sets with different sample numbers

2.3 数据处理与分析

2.3.1 数据特征与标签相关性分析

为了更加直观分析输入参数（数据特征）与输出参数（数据标签）之间的关系，采用皮尔逊（Pearson）相关系数衡量数据特征与标签之间的相关性，公式为

式中，ρx,y为相关系数，E为期望，μ为均值，σ为标准差。

Pearson 相关系数可以衡量影响因素之间的线性相关程度，利用LHS 方法生成1800 个分布均匀且填充性较好的试验样本。表2为波浪载荷影响因素与响应之间的关系，通常船中载荷为最大值，因此研究船中位置处波浪载荷影响因素与波浪载荷之间的关系很有必要。从表中可得出，航速、周期、波高、航向角，即输入参数之间Pearson相关系数几乎为0，无相关性，表明波浪载荷的影响因素之间相互独立，互不干扰。从波浪载荷影响因素对响应值的相关程度来看，波高与垂向弯矩的Pearson相关系数为0.863，呈强线性相关，水平弯矩和扭矩同理；周期与水平弯矩的值为-0.527，呈弱相关性。图7为波浪载荷影响因素与响应之间的关系图，图中可以看出周期与载荷呈三角形分布，航向角与扭矩和水平弯矩也呈三角形分布，它们之间存在一定的非线性关系。

图7 低频波浪载荷影响因素与响应值之间相关性Fig.7 Correlation between low frequency wave load influencing factors and response values

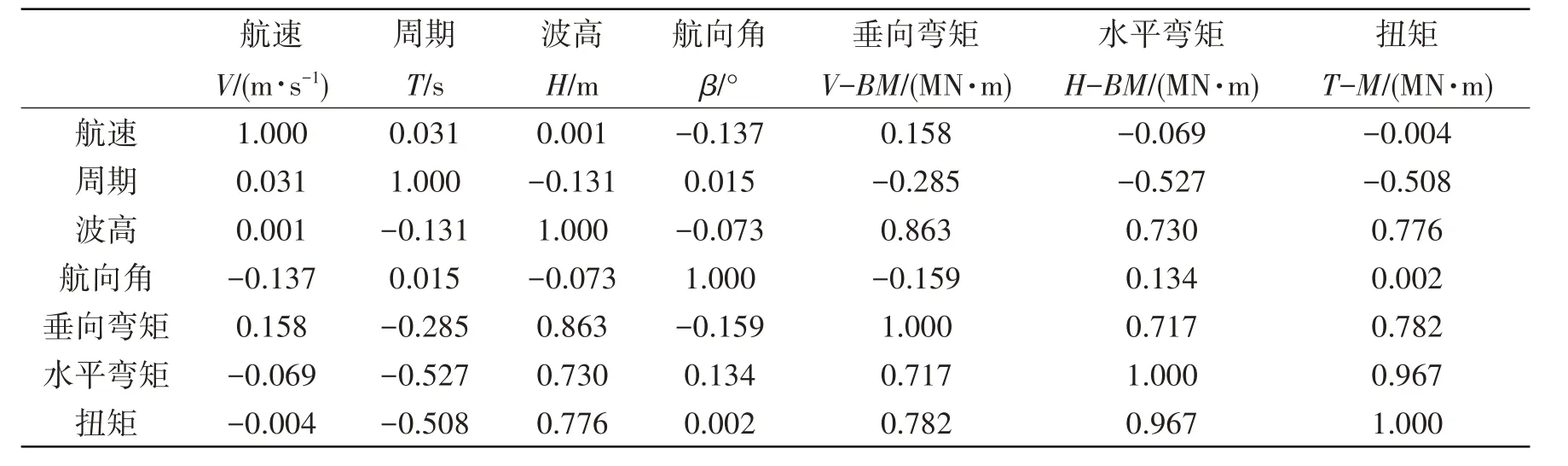
表2 波浪载荷影响因素与响应值的Pearson相关系数Tab.2 Pearson correlation coefficient between wave load influencing factors and response values

2.3.2 数据标准化方法分析

在做机器学习时，为了使不同特征变量具有相同的尺度，通常需要将样本数据进行标准化处理，也可以理解为无量纲化处理，使其实现神经元之间的信息传递，也更适用于激活函数的输入。本文采用常见的离差标准化（MinmaxNorm）方法和均值归一化（Z-scoreNorm）方法。离差标准化方法是对原始数据进行线性变换，使结果映射到[0,1 ]区间，公式为

Z-scoreNorm 方法对原始数据变换为均值为0、标准差为1的新数据，公式为

式中，平均值xˉ=，标准差s=

图8所示为采用MinmaxNorm 和Z-scoreNorm 方法的计算对比，从图中可得，两种方法测试集计算值和预测值的相关系数均大于0.99，从误差的分布来看，两者并无明显优势，MinmaxNorm 方法略好于Z-scoreNorm 方法。随后，利用两种方法训练的预报模型对指定工况沿船长的垂向弯矩进行预测，从图9可以看出，垂向弯矩沿剖面位置的预测值与程序计算值和模型试验值分布趋势也十分吻合，两种方法预测区别不大。总体而言，MinmaxNorm方法对数据处理更适用于波浪载荷智能预报。

图8 测试集计算值与预测值对比Fig.8 Comparison of calculated and predicted values for the test set

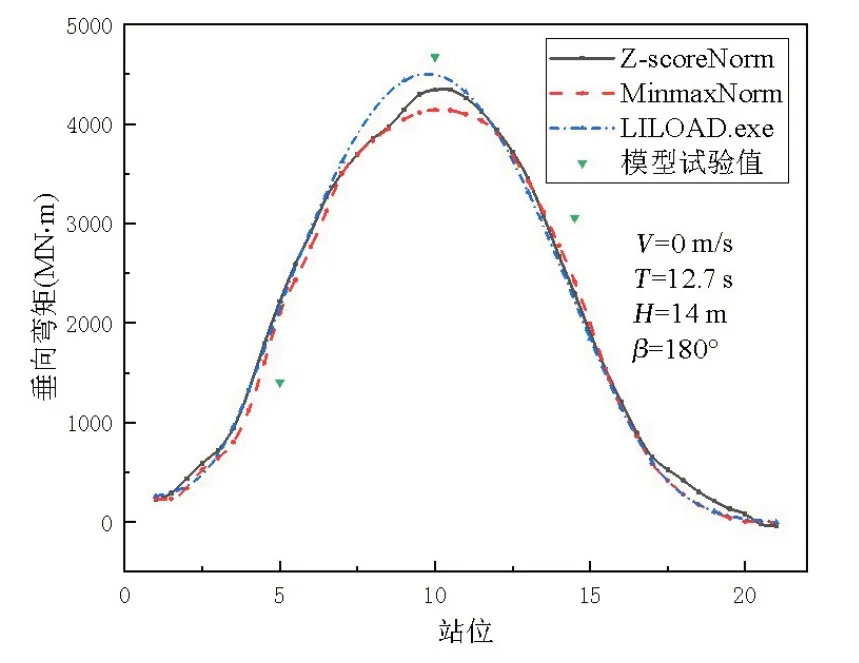
图9 指定工况下剖面位置计算值与预测值对比Fig.9 Comparison between calculated and predicted values of profile position under specified working conditions

3 超参数优化计算

通过分析发现，LFWLIP 方法的计算精度对DNN 超参数依赖性较强，为了让LFWLIP 方法的构建过程不再需要人为调参，本文选取Tensorflow[19]库搭建DNN 模型、Hyperopt 库搭建贝叶斯优化[20]（Bayesian optimization, BO）算法，将BO 算法和DNN 结合建立了自动化机器学习（automated machine learning,AutoML）方法。

3.1 自动化机器学习方法

BO 算法作为超参数优化领域最先进的方法之一，它可以被应用于神经网络架构搜索以及元学习等先进的领域。现代几乎所有在效率和效果上取得优异成果的超参数优化方法都是基于贝叶斯优化的基本理念而形成的。具体实现流程如图10 所示，首先定义DNN 超参数变量及约束条件；其次定义优化函数，设置BO算法相关参数；通过若干次网络训练达到收敛条件，输出最优参数，即测试集Rmse最小的网络模型。

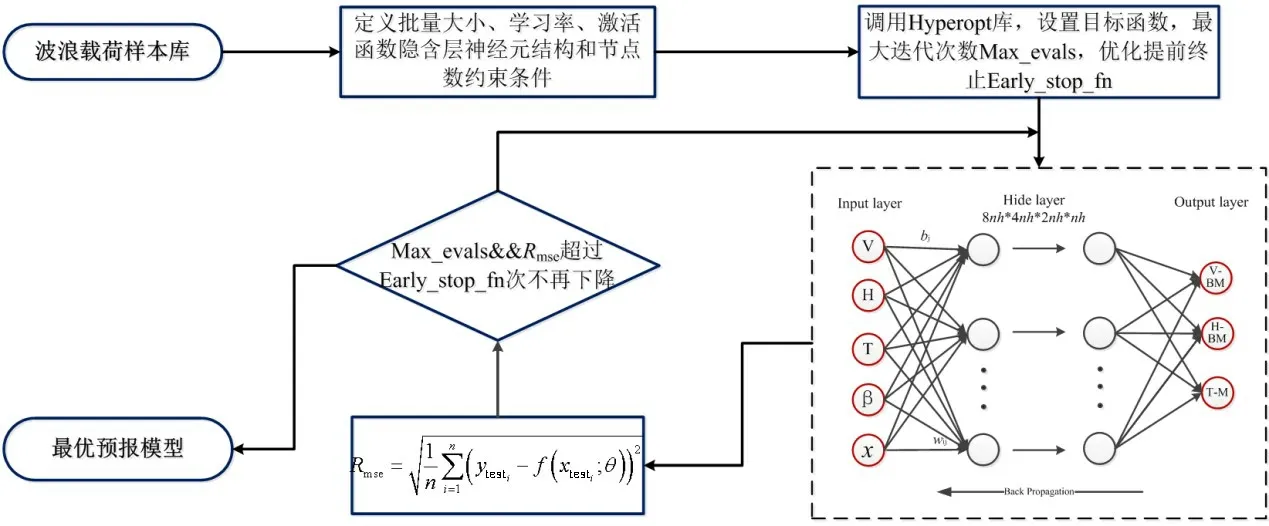
图10 基于BO-DNN的自动化机器学习方法Fig.10 Automatic machine learning method based on BO-DNN

3.2 优化数学模型

DNN 的模型参数设置见表3，网络超参数有学习率lr、隐藏层神经元数nh、激活函数af和批量大小bs。网络超参数的设置很大程度影响了LFWLIP 方法的使用效果，因此将对以上四个参数进行优化，构建网络优化数学模型为

表3 网络结构参数Tab.3 Network structure parameters

3.3 优化结果

优化数学模型见式（7），如表4 设置BO 算法参数，其中最大超参数搜索次数为3000，超参数搜索选择一种利用高斯混合模型来学习超参模型[20]的算法，称为（Tree-structured ParzenEstmator,Tpe）。为了节省计算资源，激活提前停止寻优功能，即当目标函数经过500 次后不再下降时结束优化。在超参空间中搜索1157 次后，测试集Rmse经过500 次搜索不再下降跳出循环，Rmse最终优化结果为0.011 24（见图11 所示）。

表4 BO算法优化结果Tab.4 Optimization results of BO algorithm

为了验证优化后LFWLIP预测效果，在中国船舶科学研究中心耐波性水池进行了某船波浪载荷模型试验，工况选取了0 kn、180°顶浪、波高14 m 和周期12.7 s，测量参数包括5站、10站和14.5站分段船体梁的垂向弯矩。图12 给出了LFWLIP 方法计算的沿船长方向40 个剖面的垂向弯矩值、切片理论和模型试验的对比，从图中可以看出垂弯沿船长分布的计算值与LFWLIP 方法预测值趋势一致，误差较小，预测精度较高，结果表明超参数优化效果较好。

图12 垂向弯矩试验值与预测值对比Fig.12 Comparison between test value and predicted value of vertical bending moment

4 多源波浪载荷融合

经优化后的LIWLIP模型可以快速且准确地计算任意航速、波高、航向角、周期和剖面位置的线性波浪载荷。本文利用模型试验波浪载荷传递函数结果和ISSC 双参数谱进行短期预报获得720个工况数据。模型试验还测量了不规则波工况下各分段船体梁的垂向、水平弯矩和扭矩，主要用于研究不规则波中船体结构响应，也称为高精度数据集，总共有66 个工况，包括了低频和高频成分。

高精度数据较为真实地反映了实际海况下的短期预报值，如何在较少高精度数据的基础上利用低精度数据提升预报模型的性能是亟待解决的问题。本文将低精度数据作为源域、高精度数据作为目标域，建立了一种基于迁移学习的多源波浪载荷融合（multi-source wave load fusion, MSWLF）方法，MSWLF 具体流程如图13所示。

4.1 迁移学习

图13 多源波浪载荷融合方法流程图Fig.13 Flow chart of multi-source wave load fusion method

为了泛化模型试验不规则波工况下的波浪载荷短期预报，本文将数值计算数据、规则波模型试验传递函数作为源域，模型试验不规则波工况下的波浪载荷预报作为目标域，通过迁移学习训练出精度较好的多源波浪载荷融合模型。如图14 所示，第一次迁移学习（first transfer learning net,FTLN）模型泛化和修正了不规则波工况下波浪载荷短期预报的线性成分，在训练的过程中，冻结LFWLIP 模型中的网络参数，添加两层神经元，以模型试验数据测试集计算损失函数；MSWLF 模型修正了不规则波工况下波浪载荷短期预报的非线性成分，在训练的过程中，冻结FTLN 模型中的权重和偏置，添加两层神经元，以模型试验数据测试集计算损失函数，通过LFWLIP模型的两次迁移得到高精度的多源波浪载荷融合模型。

图14 基于迁移学习的多源波浪载荷融合模型Fig.14 Multi-source wave load fusion model based on transfer learning

图14构建了数值计算和模型试验数据融合的MSWLF模型，网络参数设置如表5所示，其中FTLN和MSWLF模型的超参数在下文进行贝叶斯优化，得到适用于模型试验数据训练的网络超参。

表5 MSWLF网络结构参数Tab.5 Structure parameters of MSWLF network

4.2 模型试验线性波浪载荷修正

在模型试验数据的处理中，通常会将时域测量数据进行高低频分离，其中低频为线性成分，高频为砰击和浪等非线性成分。为了尽量融合更多的真实数据，本文首先修正波浪载荷线性成分，充分利用不同波高下规则波中分段船体梁的垂向、水平弯矩和扭矩的传递函数。如图14所示，构建FTLN 模型的过程中，在LFWLIP 模型的基础上增加两层网络，其中一层为输出层。训练FTLN 模型时，冻结了LFWLIP 模型的所有参数，相当于保留了数值计算方法的历史经验和知识，只需训练外加两层神经元的网络参数，这一步理解为修正数值计算和模型试验之间的误差。为了得到测试集较优的Rmse，采用BO算法对FTLN模型超参进行优化。第一阶段迁移学习超参数优化数学模型为

BO 算法参数设置同第3章，最大超参数搜索次数为3000，为了节省计算资源，激活提前停止寻优功能，即当目标函数经过500 次后不再下降结束优化。如图15 所示，通过在超参空间中搜索553 次后，测试集Rmse经过500 次搜索不再下降跳出循环，Rmse最终优化结果为0.0207，FTLN 模型超参数优化结果如表6 所示。以模型试验不同工况下线性波浪载荷为数据集，如图16 所示，通过对FTLN 模型网络参数训练，训练集和测试集得到了较好的Loss值。

表6 FTLN模型优化结果Tab.6 Optimization results of FTLN model

图16 FTLN模型训练过程中训练集和验证集的Loss值Fig.16 Loss of FTLN model training set and validation set

图15 FTLN模型测试集的Rmse优化收敛图Fig.15 Optimization convergence of FTLN model test set Rmse

为了验证FTLN 模型的修正效果，对模型试验测试集工况预测值误差进行分析，从图17 可以看出，载荷较小时误差相对而言较大，但也基本上在10%以内。如图18所示，本文选取工况为18 kn、周期10.5 s、波高11.8 m和斜浪150°预测波浪载荷沿剖面分布，通过对比得出，经过第一阶段知识迁移后的FTLN模型的修正结果较好，与模型试验误差较小。

图17 FTLN模型测试集预测值和试验值对比Fig.17 Comparison between experimental and predicted values of FTLN model test set

图18 某工况试验值与FTLN模型预测值沿站位分布对比Fig.18 Comparison between experimental and predicted values of FTLN model distribution along the station in a working condition

4.3 模型试验非线性波浪载荷修正

不规则波模型试验对船舶结构强度评估至关重要，然而人力、物力限制了试验次数，研究者通常利用理论计算加以补充，但是对如砰击、甲板上浪等强非线性理论计算精度与耗时目前还没有较好的解决方法。在第4.2 节中利用理论计算和规则波试验数据得到了模型泛化后精度较好的线性波浪载荷结果。如图13所示，本节考虑利用数值计算和模型试验数据二次融合的方法泛化不规则波工况下的波浪载荷预报模型，对FTLN 模型进行第二次迁移得到测试集满足精度要求的MSWLF 模型。具体流程见图14，在FTLN 模型基础上增加两层网络，其中一层为输出层。训练MSWLF 模型时，冻结了FTLN 模型的所有参数，相当于保留了波浪载荷线性成分预报的历史经验和知识，只需训练外加两层神经元的网络参数，这一步解释为修正模型试验波浪载荷非线性部分。为了得到测试集较好的Rmse，采用BO算法对MSWLF模型超参进行优化，优化数学模型为

由于不规则工况较少，加上站位影响总共66 个工况，为了防止模型过拟合，在隐含层网络参数设置中加入了Dropout 项和L2 正则化[16]，因此贝叶斯优化模型设计变量加入了Dropout 项参数pm，见公式（9）。为了得到测试集较好的Rmse，采用BO 算法对MSWLF 模型超参进行优化。如图19 所示，通过在超参空间中搜索1141 次后，测试集Rmse经过500 次搜索不再下降跳出循环，Rmse最终优化结果为0.107 192，MSWLF 模型超参数优化结果如表7 所示。以模型试验不规则波工况为高精度数据集，为了更好地捕捉到边界处的信息，根据载荷特征在船艏艉站进行了约束。如图20 所示，通过对MSWLF模型网络参数训练，训练集和测试集得到了收敛性较好的Loss值。

表7 MSWLF模型优化结果Tab.7 MSWLF model optimization results

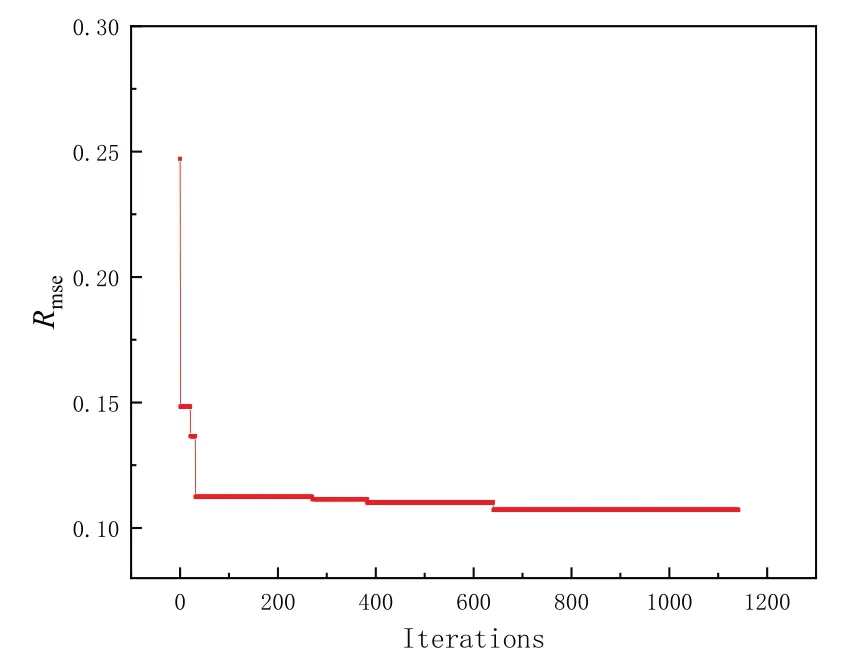
图19 MSWLF模型测试集的Rmse优化收敛图Fig.19 Optimization convergence of MSWLF model test set Rmse

为了验证MSWLF 模型的修正效果，对不规则波试验测试集工况预测值误差进行分析，从图21可以看出，载荷误差基本在20%以内。如图22 所示，选取工况为18 kn、周期12.7 s、波高14 m 和斜浪150°预测波浪载荷沿剖面分布，通过对比得出，经过第二阶段知识迁移后的非线性波浪载荷修正结果较好，与模型试验测试集误差小于20%。

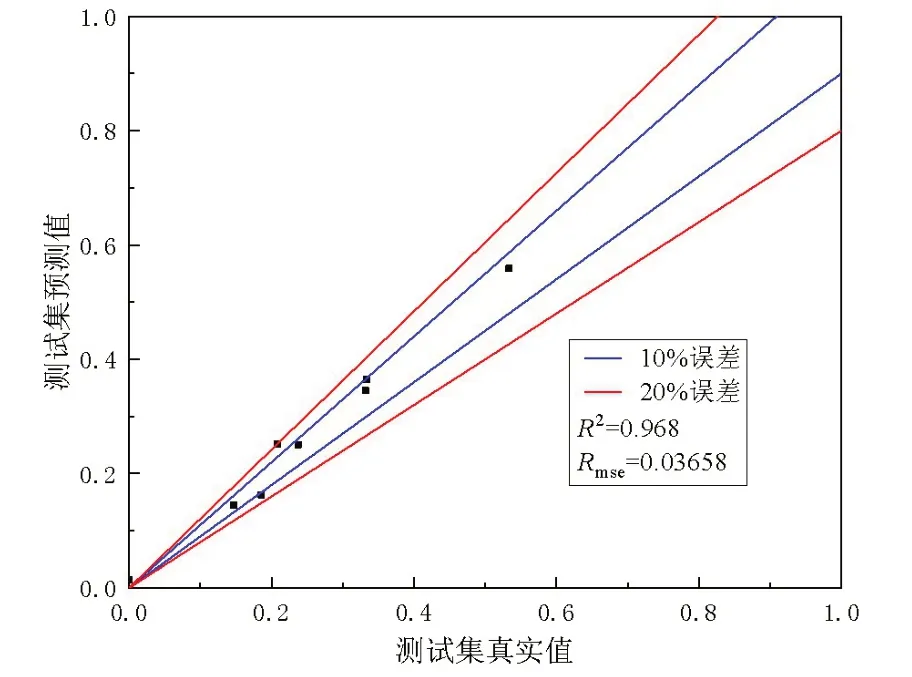
图21 MSWLF模型测试集试验值和预测值对比Fig.21 Comparison between experimental and predicted values of MSWLF model test set

图22 某工况试验值与MSWLF模型预测值沿站位分布对比Fig.22 Comparison between experimental and predicted values of MSWLF model distribution along the station in a working condition

经研究发现，迁移学习成功将源域一和源域二训练得到的知识迁移到目标域中，MSWLF 模型泛化了小样本模型试验，在波浪载荷理论、试验设计、数据标准化处理、模型试验和迁移学习等方法融合基础上，能够以较高的精度对全域空间中任意航速、波高、周期、航向角和剖面位置处的波浪载荷进行预测。

5 结 论

为了泛化模型试验工况，以数值计算数据作为源域一，规则波模型试验数据作为源域二，不规则波模型试验数据为目标域，基于迁移学习建立多源波浪载荷融合方法。通过某船开展了分析工作，得出以下结论：

（1）结合试验设计方法、数据处理方法、线性切片理论和深度神经网络建立了LFWLIP方法；采用LHS试验设计方法，样本数大于1600，测试集的计算值和预测值R2达0.99以上，Rmse小于0.02；Minmax-Norm方法对数据进行处理更适用于波浪载荷智能预报。

（2）将BO 算法和DNN 结合建立了AutoML 方法，构建了适用LFWLIP 的优化数学模型，优化后均方根误差Rmse为0.011 24，与试验对比得到了高精度的LFWLIP模型。

（3）迁移学习成功将源域一和源域二训练得到的知识迁移到目标域中，基于两次修正的MSWLF模型泛化了小样本的模型试验数据，能够以较高的精度对全域空间中任意航速、波高、周期、航向角和剖面位置处的波浪载荷进行预测，载荷误差在20%以内。

（4）该方法也存在不足，比如外插推断的验证、不同船型的波浪载荷预测等，后续将针对性地进行深入研究。