一种基于改进流固耦合力求解的浸没光滑点插值法

杨博睿，张桂勇，2，王双强，严博骞，王 鹏

（1.大连理工大学工业装备结构分析国家重点实验室；船舶工程学院，辽宁大连 116024；2.高新船舶与深海开发装备协同创新中心，上海 200240）

0 引 言

流固耦合是船舶与海洋工程领域中的一种常见现象，它涵盖了非定常流体流动和固体大变形分析，具有十分重要的研究价值。1972 年，Peskin 提出浸没边界法（IBM）[1]，并首次应用了非贴体网格。该方法无需进行网格重构操作，极大地节省了计算资源，因此十分适合应用于求解固体域发生较大变形或移动的流固耦合问题中。在此基础上，浸没类方法的思想也与有限元法相结合，应用到流固耦合问题的求解当中，取得了较好的模拟效果[2]。

光滑点插值法（S-PIM）是由Liu和Zhang[3]基于广义梯度光滑度技术[4]提出的一种插值方法。与传统的有限元方法（FEM）[5]相比，S-PIM 可以在使用简单的低阶单元时进行高阶插值，软化了模型刚度，提高了计算精度并降低了对网格质量的依赖性。本文采用的浸没光滑点插值法（IS-PIM），便是在浸没类方法的框架下，采用光滑点插值法作为固体求解器的一种流固耦合计算方法[6]。

在传统的ISPIM 求解过程中，流固耦合力是通过虚拟流体拉格朗日网格计算的[7]，并没有考虑固体边界的速度梯度。所以这种计算方式会导致边界处粘性力被忽略。本文提出一种基于真实流体欧拉网格求解，并通过插值传递到固体节点的流固耦合力施加方法。该方法直接通过流体节点的额外动量变化求解流固耦合力，可规避需单独进行粘性力计算的缺点，程序流程简单。本文对新方法与传统求解方式进行对比介绍，并通过数值算例展示新方法在提高计算精度方面的作用，同时验证流固耦合力条件和速度条件在节点动量改变方面的等效性，强化新方法的理论基础。

1 浸没光滑点插值方法介绍

1.1 流固耦合控制方程

浸没光滑点插值法采用与直接力法相似的思路，将边界处原本复杂的流固耦合作用转化为动量方程中的体力，施加到不可压缩粘性流体控制方程，即Navior-Stokes 方程中，以表示耦合作用对流场的影响：

文中统一采用右上角标f、s、fc 分别表示所属区域为流体域、固体域和虚拟流体域，FSI表示流固耦合。上式中，vf表示流体速度，Pf表示流体压力，Ff,FSI表示流体受到的流固耦合力，g为重力加速度。整个流固耦合系统控制方程可以分成三部分。

（1）不可压缩粘性流体的控制方程：

（2）固体运动方程：

式中，ρs、us和Ps分别为固体的密度、位移和第一类皮奥拉-基尔霍夫应力。

（3）流固耦合系统的速度条件和力条件：

1.2 流体控制方程的求解

本文在流体求解时采用了基于特征线算子分离的半隐式CBS方法[8]。该方法基于特征线理论，以流体守恒方程为基础，可以得到计算简单的显式格式，同时还具有较好的收敛性，消除了稳定性条件的限制[9]。通过使用三节点三角形单元对流体域进行离散，单元的速度和压力值可以表示为

文中统一采用右下角标表示变量指代的单元和方向。其中大写字母代表节点序号，小写字母表示方向。左上角标则表示时刻。如式（5）中，ΦfJ为流体单元第J号节点的形函数，nPfJ、nvfJi分别表示t=n时刻流体节点J的压力值和i方向的速度（i=1,2分别表示x方向和y方向）。

完成空间和时间离散之后，CBS方法对流体从n时刻到n+1时刻的求解可简单概括为三个步骤。

步骤二：利用中间时刻速度和压力边界条件求解第（n+1）时刻的流体压力n+1PfJ，

步骤三：利用当前压力值和速度边界条件求解第（n+1）时刻处的流体速度，

1.3 固体控制方程的求解

非线性固体的求解采用光滑点插值方法S-PIM。光滑域构造格式如图1所示。

固体单元采用的光滑函数W(Xs)为

图1 边基光滑域构造格式[10]Fig.1 Construction of edge-based smoothing domain[10]

式中：Ji表示光滑域内的第i个节点；Sˉ为光滑皮奥拉-基尔霍夫第二应力，为偏应力Sˉdev和体积应力Sˉvol之和。

2 改进的流固耦合力求解方式

2.1 施加流固耦合速度条件

虚拟流体节点需要施加耦合速度条件，以此来保证与固体的同步运动。由于采用非贴体网格，节点速度信息的传递需要通过形函数插值实现：

2.2 施加流固耦合力条件

在求解固体域时，需要将流体求解所得到的力条件传递给虚拟流体域，作为流固耦合力条件。虚拟流体的动量方程可写为

式中，力Ffc保证了虚拟流体节点速度与固体节点速度相同的虚拟流体假设，其本质可看作为流固耦合力。在原始IS-PIM 的力条件施加过程中，粘性力成分是在保证虚拟流体与固体拥有相同的运动响应的基础上，通过速度梯度求得的：

2.3 基于欧拉网格的流固耦合力求解

原始IS-PIM 方法是基于虚拟流体拉格朗日网格求解流固耦合力，进而施加力条件的。由于真实流体网格与固体网格不完全重合，因此会导致流固边界处的粘性力被忽略，产生数值误差，在模拟大刚度或低雷诺数流动问题时尤为明显。因此，本文提出一种基于欧拉网格的求解思路。不同于传统的求解方式，该方法直接通过流体控制方程求解各个流体单元所受到的流固耦合力，然后作为耦合力条件施加到固体节点上。

根据CBS计算过程，由式（6）可得到基于欧拉网格求解时的动量方程为

再考虑流固耦合速度条件的作用，将动量方程改写为

联立以上二式，可以得到欧拉网格下计算出的流体节点的流固耦合力：

该公式形式上与牛顿第二定律公式类似，体现了流固耦合力与流体节点动量变化的关系，并将在后续的数值算例部分进行验证。接下来只需通过形函数进行单元应力的插值，将流体节点流固耦合力传递给固体节点，作为求解固体域时的耦合力条件即可，过程如图2所示。

图2 应力插值过程示意图Fig.2 Schematic diagram of stress interpolation process

3 数值算例

3.1 圆柱绕流

首先对低雷诺数下圆柱绕流问题进行模拟，验证本方法对流固耦合力计算的精度及其有效性。设置圆柱直径D=1 m，流域长度L=32 m，宽度B=16 m。几何域信息如图3 所示。物理属性方面，流体为不可压缩粘性流体，密度设为ρf=1000 kg/m3；固体圆柱为固定的刚体。流场左侧边界有沿X方向、速度为Vf=1 m/s 的来流。分别采用固体节点数为380、575 和743，以及流体节点数为22 141、31 161 和55 940的网格对雷诺数为100时圆柱绕流的阻力系数Cd进行了对比。网格划分如图4所示，最终模拟结果如表1 所示。可以看到随着固体节点或流体节点数的增加，相同雷诺数下圆柱的阻力系数变化并不大，结果已收敛。

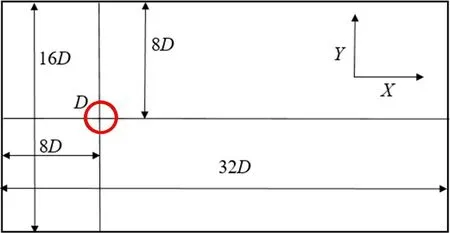
图3 圆柱绕流的几何域信息Fig.3 Geometric model of flow past a cylinder

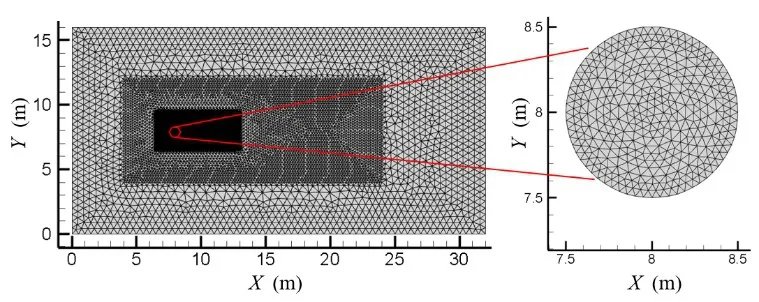
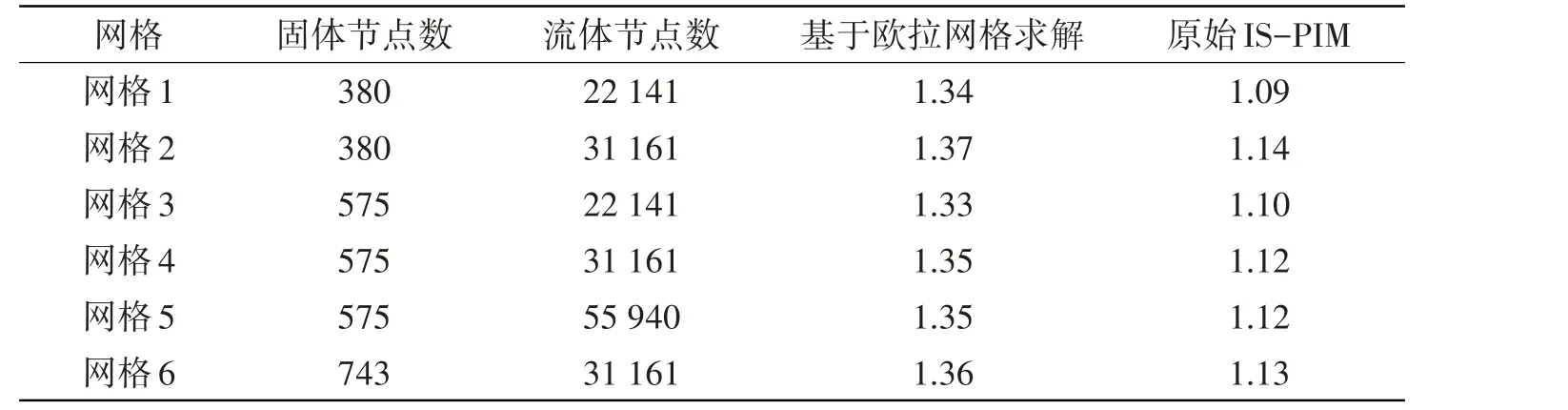
表1 Re=100时，不同方法在各网格下求得的CdTab.1 Summary of Cd obtained by 2 methods under different mesh sizes when Re=100

验证网格的收敛性后，选用网格5 对雷诺数为20、40、100 和200 时的圆柱绕流现象进行了模拟。将圆柱绕流的阻力系数Cd与其他研究学者的结果以及基于拉格朗日网格进行额外修正粘性力的ISPIM算法[12]进行了对比，结果如表2所示。

表2 两种方法在不同雷诺数下求得的CdTab.2 Summary of Cd obtained by 2 methods under different Re

结果显示，新提出的基于欧拉网格的求解方式无需进行边界粘性力的修正，即可较好地模拟低雷诺数下的圆柱绕流现象，而原始ISPIM 由于无法计算流固边界的粘性力，对阻力系数的模拟偏小很多。图5 为各雷诺数下圆柱绕流稳定后阻力系数的对比。

接下来对新方法模拟的流场速度、压力云图进行分析。图6～7 分别为不同雷诺数下流场稳定后速度云图及流线。可以看出，在低雷诺数流动下，速度云图在圆柱上下两侧呈对称分布，且圆柱两侧的流线较为平滑。随着雷诺数的增大，流场波动变得剧烈，圆柱后形成的旋涡结构也越发明显。

图5 各雷诺数下求得的Cd与其他学者结果对比Fig.5 Comparison of Cd under different Re with those of other researches

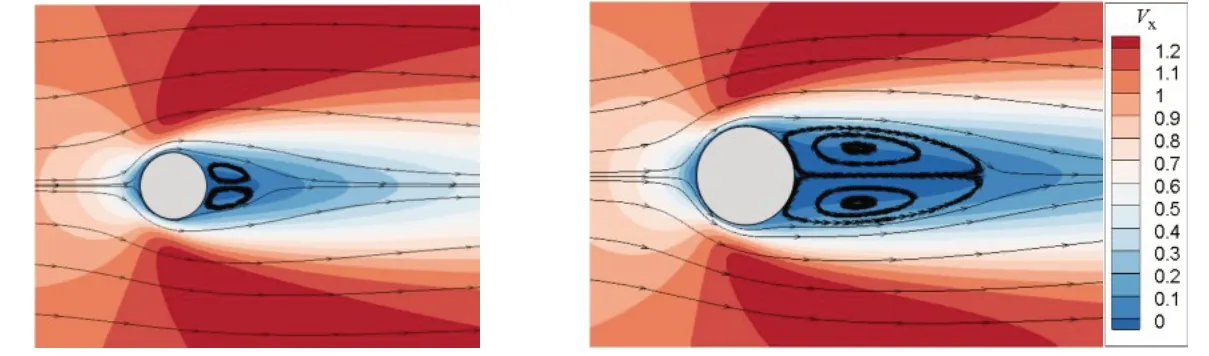
图6 基于欧拉网格模拟速度云图及流线（左：Re=20，右：Re=40）Fig.6 Velocity contour and streamline of fluid for Re=20(left)and Re=40(right)

图7 基于欧拉网格模拟速度云图及流线（左：Re=100，右：Re=200）Fig.7 Velocity contour and streamline of fluid for Re=100(left)and Re=200(right)

图8 基于欧拉网格模拟Re=100时圆柱绕流的压力云图Fig.8 Pressure contour of fluid for Re=100

图9 基于欧拉网格模拟Re=200时圆柱绕流的压力云图Fig.9 Pressure contour of fluid for Re=200

图8～9 分别展示了Re=100 和Re=200 的压力云图，圆柱后侧能观察到明显的卡门涡街现象。在图9 中，圆柱尾流上下交替出现的低压区颜色较图8 中的更深，体现了雷诺数增大后旋涡整体强度的提高。上述模拟现象均与实际物理现象相符合。

图10 为对Re=40 时圆柱后尾涡长度的测量，表3 为测量结果与其他学者结果的对比。结果显示基于欧拉网格求解的IS-PIM能够较准确地模拟圆柱绕流的尾流和旋涡结构。

图10 尾涡长度测量示意图Fig.10 Measurement of vorticity length

表3 Re=40时流场稳定后尾涡长度大小比较Tab.3 Summary of the length of the vorticity for Re=40

3.2 圆盘沉降

圆盘受重力作用在流场中自由沉降是一个经典的流固耦合算例。设置流域宽2 cm，高5 cm。圆盘直径D=0.25 cm。物理属性方面，设置固体密度为2 g/cm3，泊松比为0.3，弹性系数Es=1.0×104g/(cm·s2)。流体密度为1 g/cm3。初始时刻流体和固体速度均为0。首先以粘性系数μ=1.25 g/(cm·s)为例，选用不同节点数的网格对圆盘在下落过程中所达到的稳定速度进行了模拟计算，结果如表4所示。图11以基于欧拉网格的计算为例，展示了不同网格下的模拟结果，可以看出随着节点数的增加，模拟结果已收敛。

表4 各网格的节点数量及不同方法模拟的下落稳定速度Tab.4 Node number of meshes and steady velocities in falling simulated by different methods

经收敛性验证后，选择网格5 进行后续的数值模拟。采用新提出的基于欧拉网格求解方式和原始IS-PIM 对粘性系数为1 g/(cm·s)、1.25 g/(cm·s)和1.5 g/(cm·s)三种情况进行模拟，几何域信息及网格划分情况如图12所示。

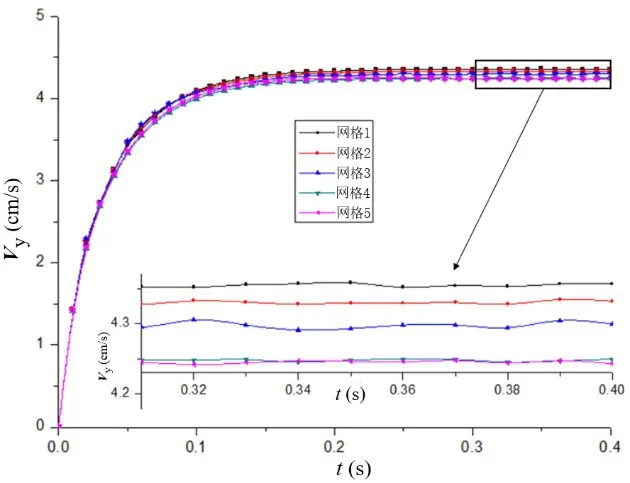
图11 基于欧拉网格在粘性系数1.25 g/(cm·s)时圆盘速度时间曲线Fig.11 Velocity-time curve with μ=1.25 g/(cm·s)solved based on Euler grid

图12 圆盘沉降的几何域及圆盘附近的网格情况Fig.12 Geometric domain of disk falling and the grid near the disk

不同粘性系数下圆盘从开始下落到达到稳定下落速度时的速度时间历程曲线如图13～15 所示，表5为最终结果及误差对比。从速度时间曲线中可以看出，0.15 s过后，圆盘的下落速度基本稳定，而原始IS-PIM 的计算方式误差非常大，这是由于流体的粘性在圆盘下落中起到非常重要的作用，而基于欧拉网格的计算方式在很大程度上弥补了这一缺陷。

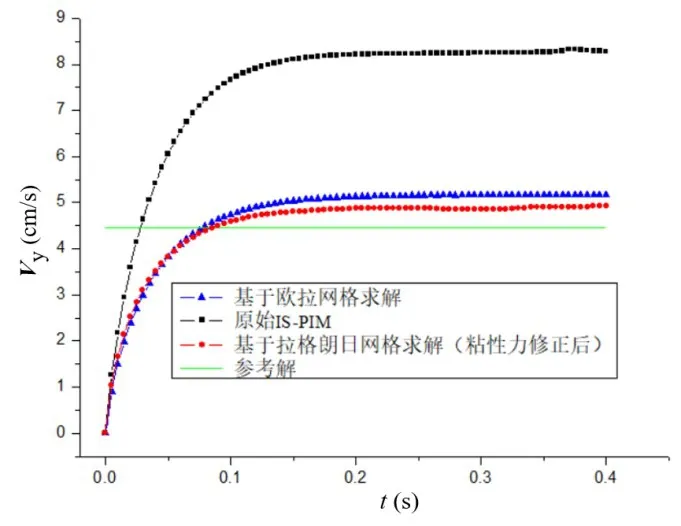
图13 粘性系数为1时圆盘速度时间曲线Fig.13 Velocity-time curve with μ=1 g/(cm·s)

图14 粘性系数为1.25时圆盘速度时间曲线Fig.14 Velocity-time curve with μ=1.25 g/(cm·s)

图15 粘性系数为1.5时圆盘速度时间曲线Fig.15 Velocity-time curve with μ=1.5 g/(cm·s)

为了说明耦合速度条件在改变流体节点动量方面与耦合力具有等效性，验证公式（18）中对流固耦合力作用的解释。在基于欧拉网格的计算模拟中，每隔0.01 s 对粘性系数为1.25 g/(cm·s)的圆盘落水的固体节点动量进行了监测，并与同时刻所求得的流固耦合力进行对比，绘制成时间历程曲线，如图16 所示。二者吻合较好，说明了该方法中所采用的施加耦合边界条件的方式来考虑原本较为复杂的流固耦合力作用的正确性。

4 结 语

表5 不同粘性系数下求得的下落中稳定速度（cm/s）Tab.5 Summary of steady velocities in falling with different viscous coefficients(cm/s)

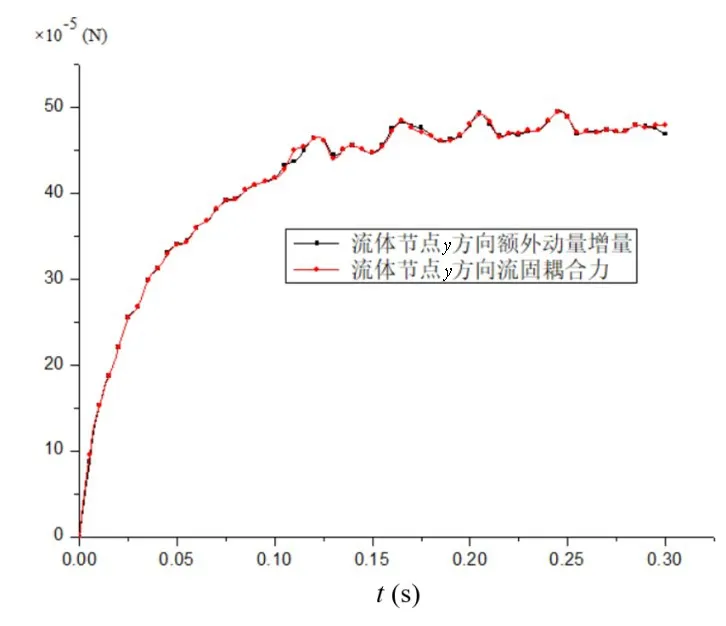
图16 基于欧拉网格模拟下流体节点在y方向上的额外动量变化与流固耦合力对比图Fig.16 Comparison of extra momentum change and FSI force of fluid nodes in y direction simulated by Euler grid

本文针对原始IS-PIM 无法计算流固边界粘性力的问题，提出了一种基于真实流体欧拉网格求解并施加流固耦合力的新方法。该方法从计算流体域全域出发求解动量方程，方法理论和求解步骤更加简单，从根本上避免了流固边界处粘性力被忽略的问题。通过数值算例的验证结果可以说明，基于欧拉网格计算流固耦合力的方法在模拟固定圆柱的绕流问题时，可以准确地体现粘性力作用，因此阻力系数的计算结果与原始IS-PIM 相比更加精确。在模拟固体运动的问题时，如圆盘沉降，精度提升的效果也十分明显，有效解决了原始IS-PIM 在模拟中忽略边界粘性力而导致圆盘下落过快的问题。在后续的研究中，可以基于该求解方式对流固边界的信息交换方式加以优化，进一步提高模拟精度。