FPSO系泊系统数值分析方法对比研究

赵 冰，姜季江，付世晓，许玉旺

（1.上海交通大学a.海洋工程国家重点实验室；b.船舶海洋与建筑工程学院，上海 200240；2.中远海运重工有限公司，上海 200135）

0 引 言

随着海洋油气资源开发走向深远海，恶劣的作业海域环境对浮式结构物关键系统的研制提出了更高的要求。通用型FPSO 是一种适用于多种海域环境的海洋油气开发平台，搭载多点、单点内转塔及外转塔等多种系泊系统，工作水深可达2000 m 左右。作为保证上部浮体正常定位作业的关键装备，系泊系统的设计分析对整个平台的安全性能尤为重要[1]。

通用型FPSO 系泊系统数值分析包括船体与系泊系统两部分。其中，船体作为刚体，受到风浪流等环境载荷作用，产生6自由度刚体运动。通常波浪载荷基于势流理论采用面元法进行频域计算，然后转至时域；而风流载荷需要开展模型试验获得，在初步设计阶段可采用已发表的近似船型风流载荷系数进行估算。系泊系统的分析主要包括解析方法和数值离散方法。解析悬链线模型忽略动态流力作用，仅考虑重力及浮力作用，且假定刚性海底无摩擦作用，从而得到船体偏移与系泊线顶端张力之间的非线性函数关系，但是这种方法只能用于系泊系统的静力计算分析[2]。另一种是离散数值模型，将系泊线视为弹性连续体，通常采用集中质量法、有限单元法或有限差分法等进行结构离散。Hall和Goupee[3]采用集中质量法对系泊线进行了建模分析，并忽略了弯曲及扭转刚度；Tang等[4]同样采用集中质量法对网箱的网衣与系泊线的动力响应进行了计算分析；Guo等[5]采用有限元法对浮式风机的悬链式系泊线回复刚度的迟滞特性进行了数值分析与研究；Kim 等[6]分别采用线性弹簧模型与非线性有限元模型模拟系泊系统对浮体运动响应进行分析，其中线性弹簧模型由于无法计及非线性因素导致结果不够准确。离散数值模型能够计及节点运动产生的修正莫里森流载荷、海洋生物附着、海土刚度及摩擦作用等非线性因素，这种方法可以用于系泊系统的非线性时域动力计算。

真实海洋环境中，船体与系泊系统的动力响应存在强烈的非线性耦合作用。在时域计算中，通常采用不同的数值分析方法来考虑二者不同程度的耦合机制，数值分析方法主要包括准静态分析方法、解耦动力分析方法以及耦合动力分析方法[7]。准静态分析方法以悬链线理论为基础，将上一时刻船体偏移位置处的系泊系统张力作为外力输入，计算当前时刻船体的偏移位置，从而得到船体6自由度运动响应以及对应的系泊水平张力[2]；解耦动力分析方法把系泊系统作为弹性体进行结构离散，将准静态方法获得的船体运动响应作为系泊系统的顶端运动边界条件，计及波流作用下的莫里森载荷等非线性因素，开展系泊系统的时域动力计算[8-9]；耦合动力分析方法将船体与系泊系统作为统一整体，建立全耦合控制方程组进行求解，这种方法由于耦合程度较高，计算结果准确性较高，但往往耗费大量计算时间[10-13]。此外，还有学者采用频域分析方法对浮式结构物的系泊系统进行耦合分析[14]，但是频域方法难以考虑所有的非线性影响因素。

本文以通用型FPSO 多点系泊系统为研究对象，基于准静态分析、解耦动力分析以及耦合动力分析等数值方法，开展系泊系统总体动力响应计算分析，通过分析系泊张力和船体运动响应等结果，对比三种数值方法的计算精度与效率，为通用型FPSO系泊系统不同设计阶段的数值分析方法提供指导性建议。

1 数值分析方法

通用型FPSO的系泊系统数值分析方法主要包括准静态方法、解耦动力分析方法和耦合动力分析方法。其中，准静态方法采用悬链线方程模拟系泊系统，解耦动力方法将准静态方法获得的船体运动响应作为系泊系统有限元模型的顶端运动边界条件，耦合动力方法将船体运动方程与系泊系统有限元动力学控制方程联立求解。

1.1 准静态分析方法

如图1所示，准静态方法将系泊系统采用解析悬链线模型进行分析，获得顶部导缆点不同偏移位置处的系泊张力，为船体运动提供系泊回复作用力-[]Km{ }x。此外，系泊系统的动态响应对船体运动还存在一种阻尼作用，在准静态分析方法中将其考虑为线性阻尼-[Cm]{ẋ}。因此，在风浪流等载荷作用下，系泊船体动力学控制方程为

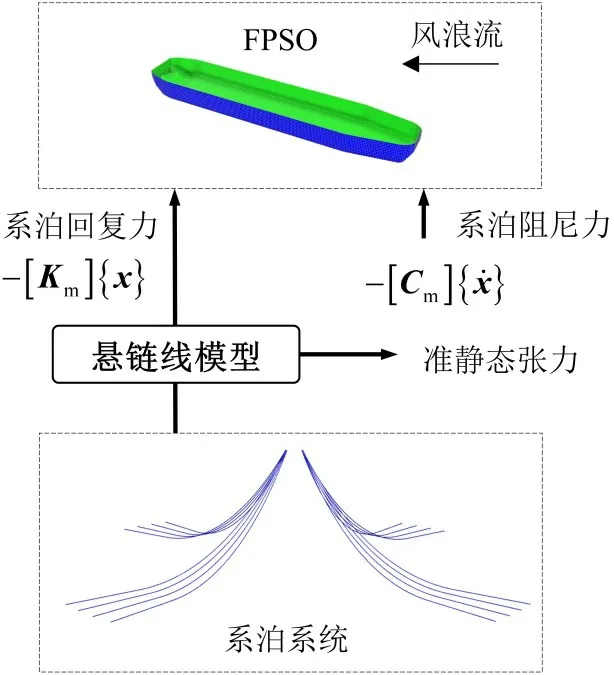
图1 准静态分析方法Fig.1 Quasi-static analysis method

1.1.1 准静态系泊刚度

在准静态分析方法中，系泊系统为船体提供的回复作用力可通过悬链线理论获得。通常单一成分的悬链线无法满足工程需求，系泊线由多种成分组成，对于每一种成分，均可采用悬链线方程模拟，在连接点处满足张力连续，形成单根多成分系泊线的悬链线方程[15]。

准静态系泊刚度是系泊系统回复力对船体位移的偏导数。根据悬链线理论计算每根系泊线在不同导缆点处的系泊张力，利用刚性船体参考点与导缆点的空间位置关系，获得系泊系统在船体参考点处的合力，其中合力水平分量对船体水平位移的偏导数为系泊系统的水平面刚度。图2给出了500 m 水深条件下一根长1200 m、直径111 mm、单位长度湿重234.4 kg/m 的锚链系泊张力水平分量与上端点水平偏移的非线性关系曲线，可以看出悬链线理论结果与商业软件Riflex和OrcaFlex 的离散数值模型静力分析结果基本相同，其中Riflex 采用有限单元法，OrcaFlex 采用集中质量法，说明悬链线理论可以获得较为准确的准静态系泊刚度。

1.1.2 准静态系泊阻尼

系泊系统对船体运动的准静态阻尼可以表示为线性阻尼，主要影响船体的水平面运动自由度（纵荡、横荡及首摇），阻尼系数阵为

图2 系泊张力水平分量-船体水平偏移关系曲线Fig.2 Horizontal component of mooring tension-ship offset relationship curve

其中，各个系数之间满足关系

式中，L为船长；Km,11为船体在初始位置处的纵荡系泊刚度；ζ为临界阻尼比，可采用衰减运动数值分析方法获得(见4.2节)。

1.2 解耦动力分析方法

如图3所示，解耦动力分析方法在准静态方法的基础上，将船体六自由度运动时历作为系泊系统有限元模型的顶端运动边界条件，同时计及莫里森流载荷、海底刚度及摩擦作用等非线性因素，开展系泊系统的动力计算，获得系泊线各个节点的动力响应。

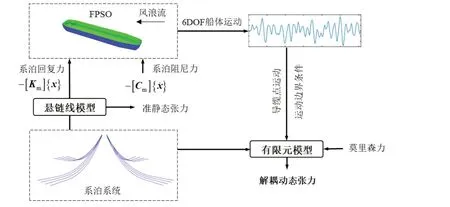
图3 解耦动力分析方法Fig.3 Uncoupled dynamic analysis method

系泊系统的动力学控制方程为

式中，[m]为系泊线质量矩阵，[c]为阻尼矩阵，[k]为刚度矩阵，{ }u、{ }u̇、{ }ü 分别为系泊线节点位移、速度及加速度列向量，{ }f为系泊线受到的莫里森载荷、海土的支持力及摩擦力等合外力列向量。系泊线顶端节点运动边界条件{uline-top} 为船体导缆点处的准静态方法获得的运动响应{xship-fairlead} 。

1.3 耦合动力分析方法

如图4 所示，耦合动力分析方法将船体动力学控制方程与系泊系统动力学控制方程通过导缆点动力响应联立同时求解，控制方程组可以表示为

式中，{Fm} 为系泊系统对船体提供的作用力向量，其中力和力矩分别由各个系泊线在导缆点处的系泊张力合成以及对船体参考点的力矩合成；[T]为船体参考点位移与导缆点位移的转换矩阵。

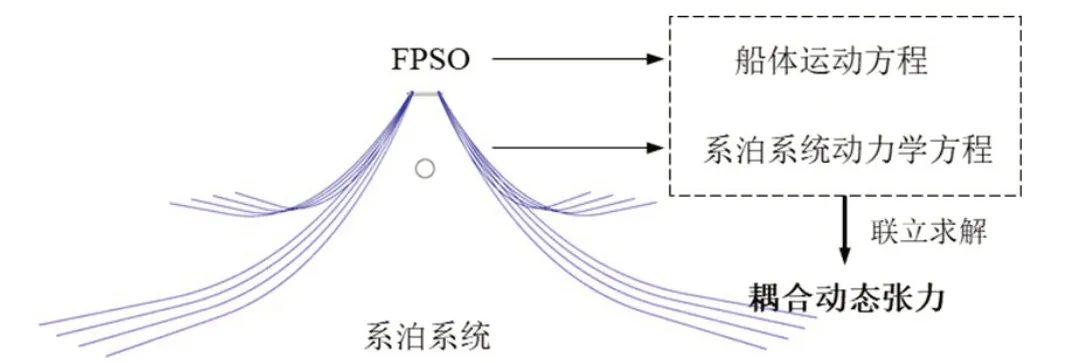
图4 耦合动力分析方法Fig.4 Coupled dynamic analysis method

2 模型参数

2.1 船体模型

本文算例FPSO 是一艘大排水量船，设计排水量高达48 万吨，船体结构参数如表1 所示。船体设计吃水下湿表面网格如图5所示，船体坐标系原点位于船体重心在水线面的投影点处。

表1 FPSO参数Tab.1 Parameters of FPSO

图5 船体湿表面网格模型Fig.5 Wet surface mesh model of the hull

图6 多点系泊系统布置方式Fig.6 Layout of multi-point mooring system

2.2 系泊系统

通用型FPSO可搭载4×4型式的多点系泊系统，如图6所示，每一组系泊线与船中线的夹角为45°，每一组的线间角为5°，系泊半径为3200 m，锚点水深为2000 m，分别编号为#1～#4、#5～#8、#9～#12 和#13～#16。每根系泊线由顶端锚链-中间钢绳-底端锚链的形式组成，具体参数如表2所示。

表2 系泊线结构参数Tab.2 Structural parameters of the mooring lines

2.3 环境载荷

船体波浪载荷基于势流理论采用面元法求解波浪速度势，再通过压力积分获得频域波浪载荷，其中平均漂移力采用Newman近似法进行计算。

风载荷计算公式为

式中，CWX、CWY、CWN分别为Isherwood 方法[16]的纵向、横向和首摇载荷系数，ρa为空气密度，Uwr为船体相对风速的运动速度，AT、AL分别为船体中横剖面和中纵剖面面积，L为船长。图7为FPSO 在不同方向θ（迎浪0°）下的风载荷系数。

流载荷计算公式为

式中，CCX、CCY、CCN分别为OCIMF 方法[17]的纵向、横向和首摇载荷系数，ρw为海水密度，Ucr为浮船体相对流速的运动速度，T为吃水，L为船长。图8为FPSO在不同方向θ（迎浪0°）下的流载荷系数。

图7 FPSO风载荷系数Fig.7 Wind load coefficients of the FPSO

图8 FPSO流载荷系数Fig.8 Current load coefficients of the FPSO

对于系泊线等细长结构物，通常采用Morison 载荷模拟洋流对其作用，单位长度圆柱体运动过程中受到的Morison载荷为

式中，D为圆柱直径；vc、un分别为流体质点和结构节点的法向速度；CD为拖曳力系数，文中无挡锚链取2.4，中间钢丝绳取1.2；Ca为附加质量系数，文中均取1.0。

3 分析工况

表3 给出了4 组计算工况的环境参数，其中波浪采用JONSWAP 谱进行模拟，风采用NPD 风谱进行模拟，流采用定常流，三者方向相同（船首迎浪），如图9所示。

表3 计算工况Tab.3 Cases for calculation

图9 风浪流方向Fig.9 Incoming directions of wind,wave and current

4 结果与讨论

本文采用WAMIT 进行船体频域水动力计算；采用SIMA 软件进行船体-系泊系统动力响应计算，其中Simo 模块用于计算船体运动响应，能够将系泊系统采用悬链线方程进行模拟，Riflex 模块采用有限元方法模拟系泊系统，用于计算系泊线的动力响应。Simo 和Riflex 两个模块可以实现解耦和耦合两种分析方法。

4.1 系泊刚度

分别采用准静态分析方法的悬链线理论和动力分析方法的有限元模型，对系泊系统在船体纵荡方向上不同偏移位置处的静态水平系泊张力进行计算，结果如图10 所示。可以看出两种方法的计算结果基本相同，且在偏移平衡位置100 m范围内水平系泊张力与偏移量呈近似线性关系，超出100 m 后表现出微弱的非线性。因此，在线性范围内，图10 中曲线的斜率可近似认为是定值，则斜率即为多点系泊系统在纵荡方向上的水平系泊刚度Km,11=40 099 N/m。考虑船体纵荡无穷附加质量A∞=3599.1 t 时，船体在初始位置的纵荡固有周期T11为

图10 系泊张力水平分量-纵荡偏移关系Fig.10 Horizontal mooring tension-surge offset relationship

4.2 系泊阻尼

首先给船体设置初始纵荡偏移66 m，分别采用耦合动力（coupled dynamic, CD）分析方法和准静态（quasi-static, QS）方法进行静水衰减数值分析，结果如图11 中黑色实线和蓝色点划线所示。可以看出两种方法的结果差别较大，主要是因为准静态方法中未计入系泊阻尼。

为了获得系泊系统对船体运动的阻尼，根据耦合动力分析结果利用对数衰减法可以得到系泊阻尼系数ζ为0.2，进而运用公式（2）～（3）获得系泊阻尼，并将其应用于准静态分析方法中进行相同的静水衰减数值分析，结果如图11 中红色虚线所示。从图11 中可以看出，在准静态分析方法中考虑系泊阻尼后，结果与耦合动力分析方法的差别较小，同时也说明系泊阻尼对船体运动响应的影响十分重要，在数值计算中应予以考虑。

图11 系泊船体纵荡静水衰减曲线对比Fig.11 Comparison of static decay curves of moored ship in surge direction

4.3 船体位移

针对表3 中的4 组分析工况，采用耦合动力分析方法（CD）与准静态方法（QS）数值计算船体在纵荡方向上的运动响应，并统计两种方法计算结果的平均值（mean）及标准差（standard deviation），如图12所示。从图中可以看出，两种方法得到的船体纵荡位移响应时历整体上基本相同，因此平均位移基本相同，而准静态方法（QS）的标准差略大于耦合动力分析方法（CD），可能的原因是准静态方法（QS）中的线性系泊阻尼略小于耦合动力分析方法（CD）中的系泊系统动态阻尼效应。

图12 船体纵荡位移响应及统计结果对比（QS：准静态方法；CD：耦合动力方法）Fig.12 Comparison of surge displacement responses and statistic results(QS:Quasi-static method;CD:Coupled dynamic method)

4.4 系泊张力

由于准静态方法的船体运动响应与耦合动力分析方法的结果基本相同，因此可以将准静态方法的船体运动时历作为系泊系统运动边界条件，即采用解耦动力（uncoupled dynamic,UD）分析方法求解系泊系统动力响应。图13 给出了不同工况下#4 和#8 系泊线分别采用三种分析方法的系泊张力时历对比结果，可以看出准静态分析方法得到的系泊张力与动力分析方法相比瞬时脉动值明显偏小，这主要是因为在准静态方法中未考虑系泊线受到的莫里森力，而两种动力分析方法获得的系泊张力变化基本相同，仅在瞬时脉动值上略微存在差异。

图13 系泊张力时历对比Fig.13 Comparison of mooring tension time histories

为了进一步比较三种数值计算方法的系泊张力差异，对系泊张力特征峰值进行Weibull极值分布拟合，将概率水平为99%的特征极值进行对比，以工况4（Hs=8 m）为例，结果如图14所示。可以看出：对于张紧的系泊线#1～#4 和#13～#16，两种动力分析方法获得的系泊张力极值明显大于准静态分析方法；对于松弛的系泊线#5～#8，三种方法结果比较接近；此外，两种动力分析方法的结果基本相同，系泊线#1的差异最大，但仅占耦合动力分析方法结果的4.96%。因此，采用解耦动力分析方法整体上可以获得与耦合动力分析方法同样精度的结果。

图14 系泊张力Weibull极值对比（工况Hs=8 m）Fig.14 Comparison of mooring tension Weibull extreme values(Hs=8 m)

4.5 计算耗时

为了比较三种数值方法的计算效率，进一步统计了三种数值方法计算每个工况所耗费的时间，如表4所示。图15所示为三种方法的耗时比率，其中准静态方法（QS）耗时最少，为耦合动力分析方法（CD）耗时的3.02%，解耦动力分析方法（UD）耗时介于准静态方法（QS）与耦合动力分析方法（CD）之间，约为耦合动力分析方法（CD）耗时的一半。因此，采用解耦动力分析方法能够在保证计算精度的基础上节省计算时间，提高计算效率。

图15 三种数值分析方法计算耗时比率Fig.15 Time consuming ratios of the three numerical analysis methods

表4 三种方法计算耗时对比Tab.4 Comparison of consuming time in the three methods

5 结 论

本文分别采用准静态分析、解耦动力分析和耦合动力分析等数值方法开展了通用型FPSO多点系泊系统总体动力响应计算分析，针对三种分析方法的船体运动与系泊张力等结果的计算精度以及计算效率进行了对比研究，主要得到以下结论：

（1）系泊系统对船体运动除了提供回复力外，还具有一定的阻尼作用，对船体运动响应影响较大，因此在准静态分析方法中需要计及系泊阻尼，可采用静水衰减耦合动力数值方法求解系泊系统的准静态线性阻尼系数；

（2）采用计及系泊阻尼的准静态分析方法获得的船体运动响应与耦合动力分析方法基本一致，但系泊张力由于未考虑莫里森力等作用而相差较大，在解耦动力分析方法中建立系泊系统有限元模型，考虑了莫里森力等多种非线性因素，得到的系泊张力与耦合动力分析方法基本相同；

（3）耦合动力分析方法耦合程度最高，但是计算耗时较长，准静态分析方法计算最快，但是无法计及流载荷导致结果存在偏差，解耦动力分析方法能够在保证系泊张力计算准确性的基础上节省计算时间，从而提高计算效率；

（4）建议在系泊系统初步设计阶段采用准静态方法确定初步设计方案，在详细设计阶段可采用解耦动力分析方法进行安全性校核。