中深层U型埋管换热器数值传热模型精准度影响因素研究

蒋向明，朱余良，郭晓凯，鲍玲玲，李振兴，郭海明

（1.中国煤炭地质总局水文地质局，河北 邯郸 056004；2.河北工程大学 能源与环境工程学院，河北 邯郸056038）

0 引言

地热资源具有储能丰富、清洁环保、稳定可靠、受季节和环境变化影响小等特点[1]，充分地开发和利用地热资源，对实现我国“双碳”目标具有重大意义。

地热能资源根据埋藏深度可分为3类：地表以下200 m以内为浅层地热能；200～3 000 m为中深层地热能；3 000 m以下为深层地热能[2]。我国陆地和海域的大地热流分布呈现为西南部（平均热流值为90 mW/m2）高于全球平局值（平均热流值为65 mW/m2）[3]，东部持平，中部（平均热流值为55 mW/m2）和西北部（平均热流值为50 mW/m2）偏低的格局。受到能源分布以及现有地下勘探、人工造储和深层钻井技术的限制，我国深层地热能开采难度较大[4]。同时，浅层地埋管地源热泵系统因其占地面积大、全年冷热负荷平衡要求高、长期运行后系统性能显著下降等原因发展受限[5]，因此中深层地热资源的开发利用逐步成为研究的焦点。中深层地源热泵系统取热的核心部件是井下地埋管换热器，换热器主要分为同轴套管式地埋管换热器及U型对接井地埋管换热器。国内外学者对同轴套管式地埋管换热器的传热机理、取热特性、系统运行模式、影响因素等进行了分析[6]～[9]，并已在工程上得到了验证[10]。

目前，少有对中深层U型埋管换热器数值传热模型模拟计算条件以及简化几何模型精准度影响的相关研究，本文通过建立的中深层U型埋管换热器数值传热模型，定量分析了控制方程的坐标变化系数等模拟条件变化对模拟结果的影响，同时对数值计算所用的不同简化几何模型的精准性进行了计算、对比，为中深层U型对接井换热器数值计算的模型研究和工程计算提供了参考。

1 传热模型

1.1 几何模型

U型对接井地埋管换热器因其优秀的取热能力而受到关注[11]，其结构如图1所示。

由于受到钻井工艺的限制，它由一个垂直井和一个L型对接井构成，L型井圆弧连接段的弯曲半径由钻井工艺和钻井直径共同决定。受限于钻井工艺，中深层U型对接井的设计施工几何尺寸并不能直接用于数值计算，需要对其进行合理而必要的简化，本文沿用国内学者[12]针对几何模型的简化方式进行模型简化。

1.2 数学模型

对模型进行合理假设是模型建立与求解的关键，对整体换热系统作出如下假设。

①下行管、水平管与上行管3部分及其换热边界内岩土体之间不存在热干扰。

②下降管、水平管和上升管内流体的流动和传热均视为一维导热问题，不考虑流体在管道横截面上的速度和温度分布，只强调平均温度和速度。

③循环流体、固井材料的热物性不变；下行管、水平管与上行管周围换热区域内同层岩土体物性均匀、一致、热物性不变；不考虑换热区域内岩土体中地下水渗流对换热的影响。

④换热器套管外壁面、回填材料以及井孔壁面三者紧密接触，忽略其接触热阻。

⑤数值模拟计算中设置的换热边界足够远，边界外岩土体温度恒定。

⑥计算区域每一位置的热流量恒定。

⑦井孔内固井材料及循环流体的温度一致，轴向导热相对于径向导热可忽略。

⑧换热器中循环水没有泄漏或其它质量交换，下降管、水平管、上升管的流速相同。

根据假设条件，将换热区域分为井孔内和井孔外两部分，井孔内传热可视为一个线热源或者是柱热源在无限大均匀介质中的非稳态传热过程，其控制方程为

式中：C为井眼通道的热容量，包括管内的流体、管壁和回填材料，J/（m3·K）；Tf为循环流体温度，℃；Tb为地热井壁面岩土温度，℃；t为时间，s；M为单位时间流经截面的流体质量，kg/s；z为轴向坐标；R为循环流体和井孔壁之间的传热热阻，K/W；ri，ro，ris，rb分别为套管的内半径、外半径、保温材料外半径和井壁外半径，m；λp，λis，λb分别为套管、保温材料及固井材料的导热系数，W/（m·K）；cf，cp，cb分别为循环流体、管道壁及固井材料的体积比热容，J/（kg·℃）；ρf，ρp，ρb分别为循环流体、管道壁及固井材料的密度，kg/m3；h为循环流体与管壁的对流换热系数，W/（m2·K）。

岩土体之间的传热可以简化为圆柱坐标系下的二维非稳态导热问题，控制方程为[13]

式中：α为土壤的热扩散系数，m2/s；T为岩土温度，℃；r为径向坐标。

考虑到换热过程中岩土体径向温度梯度与其到井壁的距离成反比，在边界处趋近于零，因此，沿径向考虑采用不等距网格划分的方法，在近地热井孔壁面处网格尺寸尽量要小，而足够远处的边界网格可以大一些，从而减小计算的数量，提高计算速度。具体方法如下：

式中：x为新坐标系下x向坐标；rc为坐标变换基数，m。

则新坐标系下控制方程转化为

在新坐标系下控制方程中x向取步长Δx划分网格，同时令

式中：r1，r2···rn为从管壁开始的第n个网格径向长度，m；β为坐标变换比例系数。

原圆柱坐标系中r向为不等距网格划分，即：

1.3 边界条件及参数选择

在地表边界温度设定以及岩土体初始温度计算过程中，一些学者以地表空气年平均温度[13]或地表年平均温度[14]为基础进行初始温度场计算，本文认为应以岩土体恒温层温度为基础进行初始温度场计算，主要原因如下。

①岩土体恒温层温度基本不受外部环境影响，可认为常年恒定，是理想的边界层。

②冬季采暖项目以全年地表平均温度作为计算标准，在时间区间上不符合实际情况。

③地表年平均温度和恒温层之间的土壤温度梯度与恒温层以下的土壤温度梯度方向是否一致，大小是否在可接受的范围内，需要进一步考证。

实验项目位于河北省邯郸市，图2为该地区浅层地下岩土体全年温度分布。

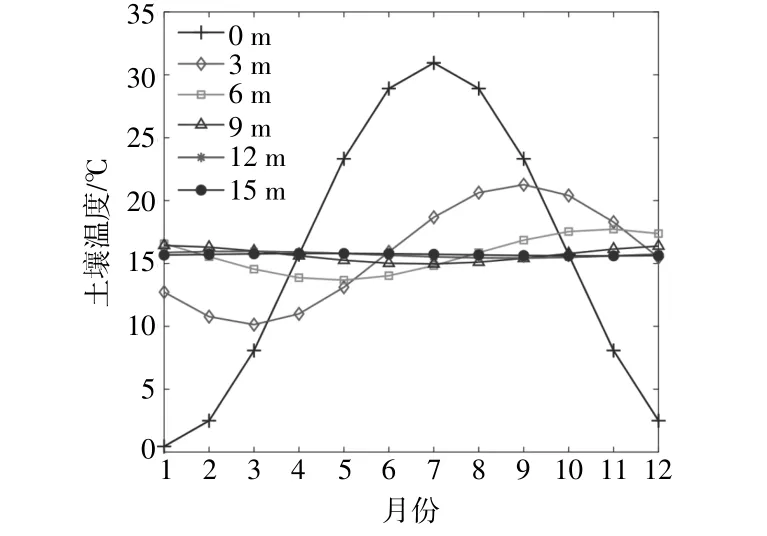
图2 邯郸地区浅层地下岩土体全年温度分布Fig.2 Annual temperature distribution of shallow underground rock and soil mass in Handan

由图2可以看出，浅层岩土体恒温层出现在地下15 m处[15]，恒温层温度为15.7℃。因此，本文中数学模型以地表下15 m作为模型上边界，以地埋管换热器下100 m作为模型下边界，径向距地埋管换热器中心100 m为右边界，均为第一类边界条件。

2 数值求解

按实验项目的实际情况，整理得到实验区域基本参数（表1），并以此作为讨论基准。

表1 系统参数Table 1 System parameter

表1中，第1层岩土体为0～420 m，第2层岩土体为420～1 040 m，第3层岩土体为1 040～1 540 m，第4层岩土体为1 540～2 290 m，第5层岩土体为2 290～2 600 m。

2.1 模型验证

利用交替方向隐式（Alternating Dorectopm Implicit，ADI）格式建立离散方程，采用追赶法直接对节点方程进行求解。通过与中科院汪集旸院士团队领衔开发并完成的“地热计算器”软件模拟结果对比发现，本文数值模型计算结果与地热计算器计算的结果在换热器温度分布及换热器出口循环水温度变化趋势上是完全一致的，换热器出口循环水温度差为0.47℃，验证了数值计算模型、计算方法以及Matlab程序的可靠性。

2.2 计算条件分析

首先以坐标变换比例β=1.2，rc=rb，径向节点数N=40、轴向步长dz=20 m、时间步长dt=180 s为基准进行计算，以模型网格的第15，35，65，95和125层进行分析，结果如图3所示。

图3 运行不同时长下不同土层径向节点位置、编号与温度对应关系Fig.3 The corresponding relationship between the position and number of radial nodes in different soil layers and temperature under different operating conditions

图4为连续运行不同时长下,径向远边界节点号与岩土体深度、温度对应关系。

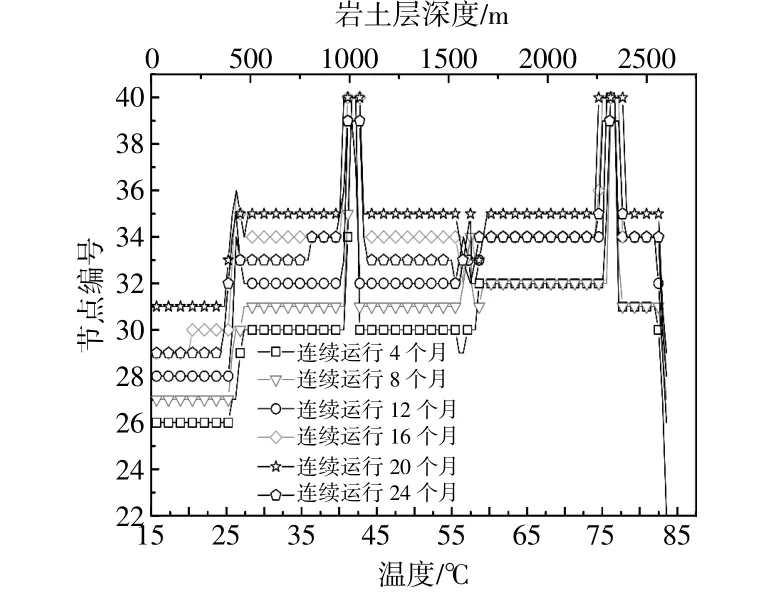
图4 连续运行24个月，径向远边界节点编号与岩土体深度、温度对应关系Fig.4 The corresponding relationship between the node number of radial far boundary and the depth and temperature of rock and soil mass when the system operates continuously for 24 months

由图4可知，不同物性岩土体径向远边界不同，径向远边界在420，1 040，1 540，2 280 m附近会发生跃迁，径向边界最远处的节点为N=40。这是由于上述4处均位于岩层物性变化的位置，其导热系数及体积热容等参数突变导致的。同时，岩土体的径向温度远边界随连续运行时间的增加而增加。

2.3 模拟条件对计算精度的影响分析

为进一步确定换热器出口温度与岩土体径向远边界之间的关系，针对岩土体径向节点的数量（N=15，20，25，26，27，28，29，30，35，40，45）变化进行了1个采暖季（2 880 h）的模拟，结果如表2所示。

表2 径向岩土体节点数及远边界对温度模拟计算精度的影响Table 2 Influence of radial rock and soil node number and far boundary on temperature simulation calculation accuracy

由表2可知，换热器出口循环水温度随径向远边界的扩大而减小，最终趋于稳定。当N＜25时，换热器出口温度随其变化波动较大；当N＞25时，换热器出口温度随其变化波动微小；当N≥29时，换热器出口温度稳定于19.820℃，取热量为1 030 kW。岩土体分层界面的突变以及径向远边界附近（26≤N≤32）岩土体传热对换热器出口温度几乎没有影响。针对计算模型中时间步长dt变化进行了模拟计算，结果见表3。由表3可知，当dt≤1 500 s时，换热器循环水出口温度的模拟结果随着时间步长的增加基本不变；当dt≥1 800 s时，下行管中循环水出口温度即出现振荡。得出在模型的模拟过程中，出口温度随时间步长的增加而发生不收敛的状况可能是突变的，这一点将在后续的研究中进一步验证。

表3 时间步长对模拟计算精度的影响Table 3 Influence of time step on simulation accuracy

针对计算模型中垂直管、水平管轴向步长变 化进行了模拟计算，结果见表4，5。

表4 平管轴向步长对模拟计算精度的影响Table 4 Influence of horizontal tube axial step size on simulation calculation accuracy

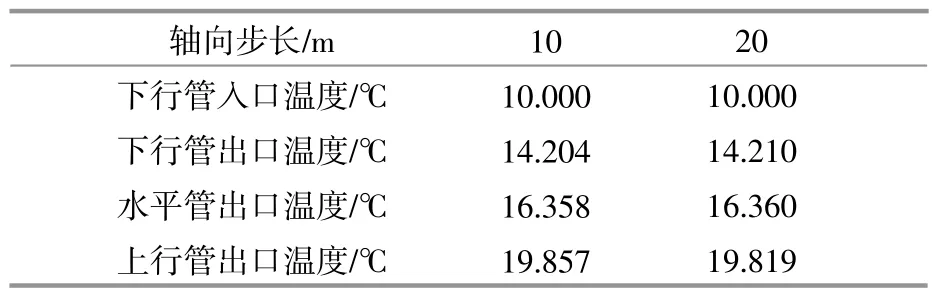
表5 垂直管轴向步长对模拟计算精度的影响Table 5 Influence of vertical tube axial step size on simulation calculation accuracy

由于管道轴向步长与每层岩土体的厚度相关，为方便比较，垂直管部分管道轴向步长仅取值10，20 m，同时将水平管的管道计算总长设置为600 m。可见对于垂直管，轴向步长dz从10 m增加至20 m，上行管的出口温度降低约0.4%，但是模拟计算耗时减少70%。对于水平管，随着dz的增加，水平管的出口温度同样逐渐降低，降低幅度小于0.02%/10 m。

针对计算模型中坐标变化比例系数β的变化进行了模拟计算，结果见表6。由表6可知，坐标变化比例系数β在一定范围内波动时，换热器出口温度随β取值增加而缓慢降低。但当坐标变化比例系数β取值较小时，时间步长的取值相应的也需要减小，否则计算结果离散。

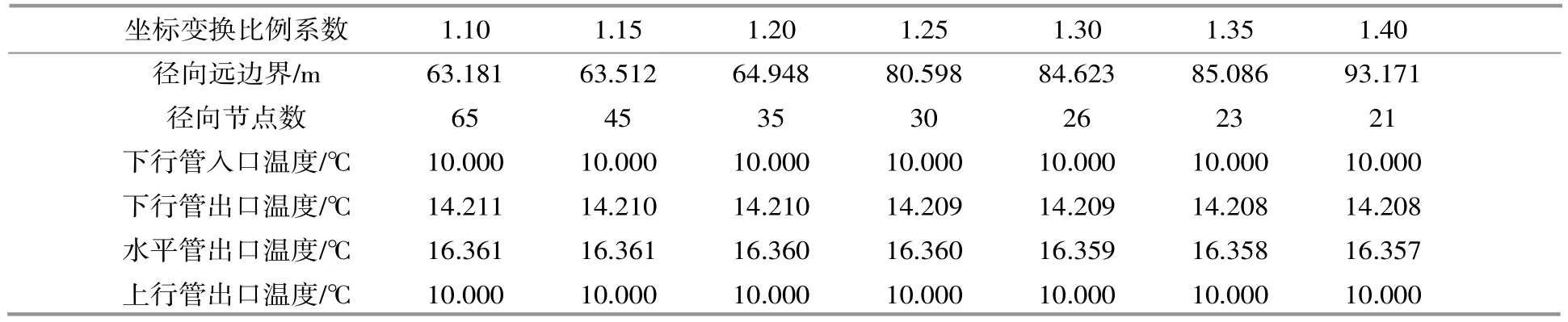
表6 坐标变化比例系数对模拟计算精度的影响Table 6 Influence of coordinate change proportion coefficient on simulation calculation accuracy

综上所述，为提高计算速度，同时保证模拟计算结果的准确性和可靠性，推荐相近项目的模型研究计算参数：坐标变换比例β=1.20，轴向步长dz=20 m，时间步长dt=1 200 s，径向远边界为55～65 m；工程设计的计算参数：坐标变换比例β=1.40，轴向步长dz=20 m，时间步长dt=1 200 s，径向远边界为15～20 m。

活动是德育课程实施的重要载体，也是学生主体性生成和发展的源泉。《新课程标准》指出：“课程设计与实施注重联系学生的生活实际，引导学生在实践中发现和提出问题，在亲身参与丰富多样的社会活动中，逐步形成探究意识和创新精神。”这从课程理念的高度，充分肯定了活动是德育课教学之必需。随着课标的深入落实，活动成了德育课教与学的中介，在课堂上教师通过活动来创设教学情境，使抽象的概念具体化，使传授的方式趣味化，使认知与情感融合化，使思维与形象统一化。活动符合小学生的认知特点，有利于学生主体人格的形成，从而促进学生知、情、意、行的全面发展。

3 简化模型精准度分析

3.1 现有模型分析

针对前文数值计算依据的几何模型，本文认为地埋管换热器计算管长、水平管与下行管、上行管连接处及其周边的热干扰是影响模拟计算结果的重要因素。

3.1.1地埋管换热器计算管长

受限于钻井工艺以及地下岩土状况，L型对接井中必然存在的圆弧连接段，而数值模型中将L型井部分直接简化为下行管+水平管进行计算，导致数值模型计算得出的循环水出口温度、地热井提取热量等结果高于真实值。

3.1.2水平管与下行管、上行管连接处及其周边的热干扰

通过前文对传热区域进行边界分析，模拟运行1个采暖季时，水平管与下行管、上行管连接处及其周边岩土体换热区域内存在热干扰，如图5所示。

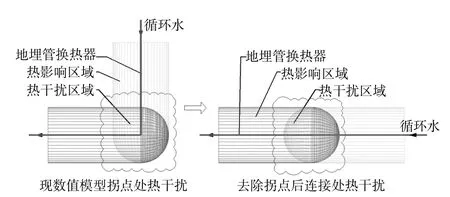
图5 数值计算模型水平管与垂直管连接处热干扰Fig.5 Thermal interference at the connection between horizontal and vertical pipes in numerical calculation model

因此，数值模型增加的下行管与水平管连接处以及原垂直井与L型对接井连接位置的无热干扰加热，均增加了理论计算的循环水出口温度。

3.2 简化模型

图6为依据图1几何模型的简化过程。

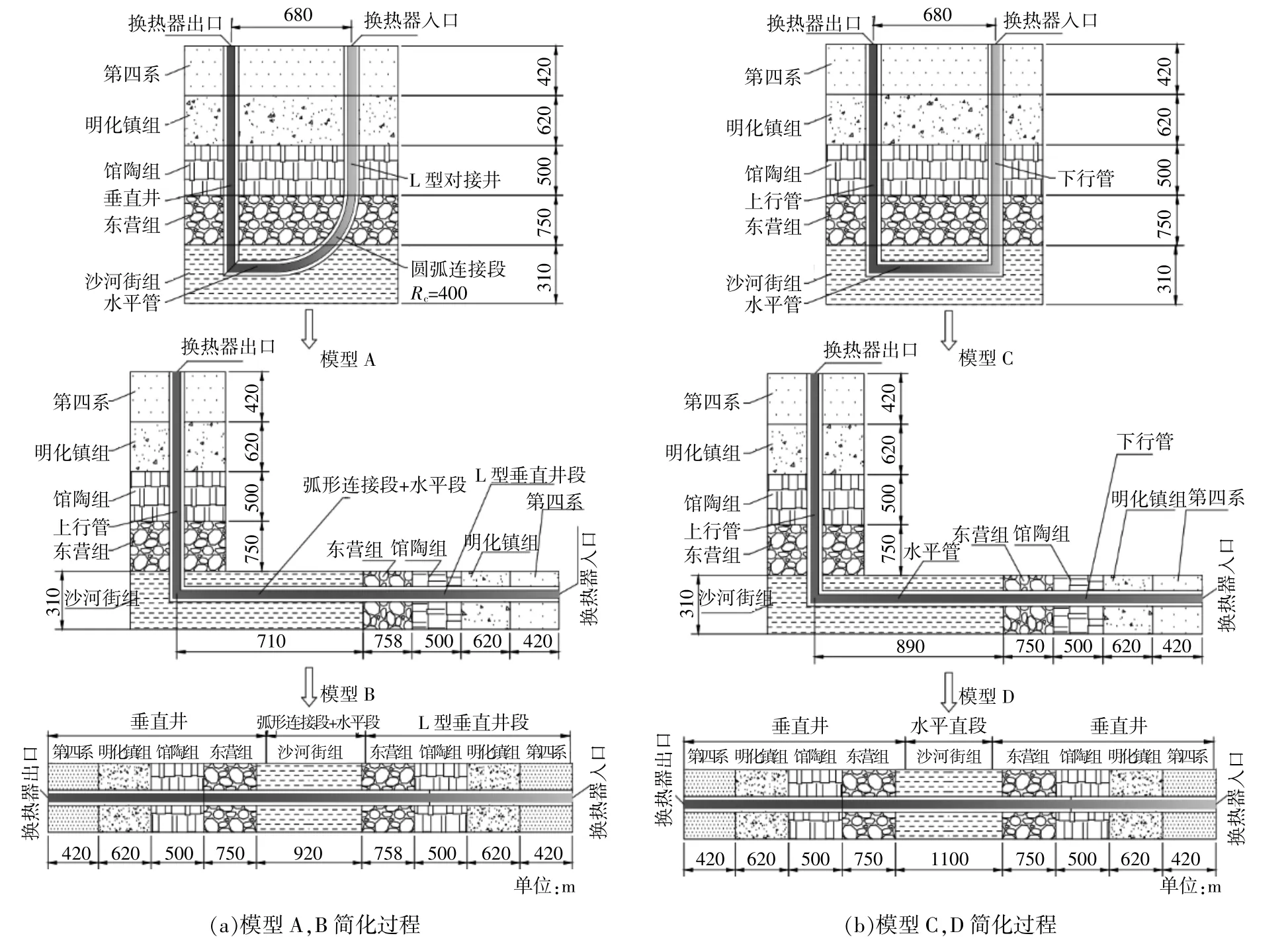
图6 几何模型简化过程及尺寸Fig.6 Geometric model simplification process and dimensions

3.2.1简化几何模型A

已知本模型中距离管中心15 m以内的岩土中的温度变换占整体温度变化的99%以上。因此针对L型对接井的圆弧连接段，以沿管道轴向20 m长度段为单元，以15 m为半径绘制了换热单元断面图，见图7。由于圆环内外侧断面弧长与换热器管道单元长度相比，变化均小于4%，所以将此圆环体换热单元视为圆柱体换热单元。模拟过程中以1个轴向步长即20 m的长度差分别对内外弧长的圆柱取热区域进行了计算，换热器出口循环水温度与以管中心长度计算的出口温度差约为±0.065℃，取热量差约为±6.8 kW，占比0.7%，偏差可接受。

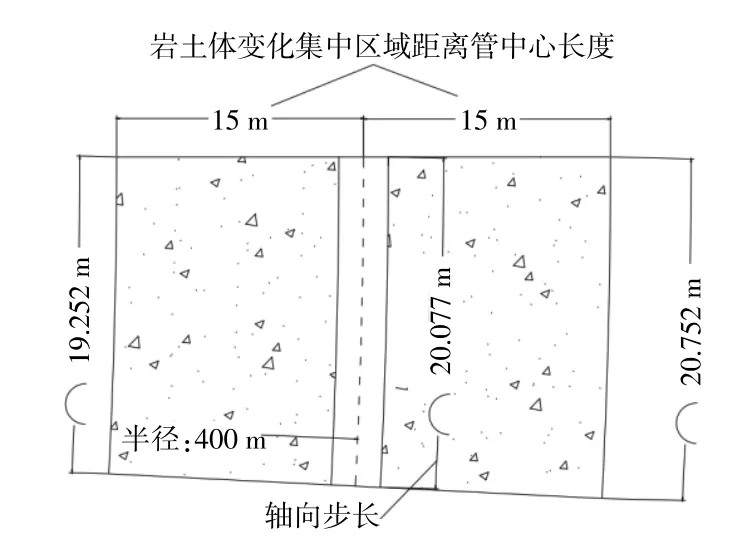
图7 圆环体换热单元断面Fig.7 Cross-section view of heat exchange unit of torus

3.2.2简化几何模型B

在简化模型A的基础上，忽略拐点处沿换热器轴线且远离换热器方向岩土体的传热，将整个换热器视为一根直管，得到简化模型B。

3.2.3简化几何模型C，D

L型对接井本身并没有连接拐点，图1中的数值计算尺寸不仅增加了计算管长，同时增加了计算拐点，但是由于两处拐点循环流体温度不同，这将对其与周围岩土体的换热产生影响，因此分为两步对其简化，得到简化模型C，D。

3.3 条件分析

为便于描述本章节中涉及模型的初始条件和边界条件，以换热器入口为起点，以模型A，C中换热器拐点、模型B，D换热器出口为终点的管道长度作为纵坐标进行描述：

其中：

对于模型A，C：

对于模型B，D：

式中：Tg为岩土体恒温层温度，℃；L为管道计算深度，m；L1为物理模型中下行管竖直管段长度，m；L2为物理模型中下行管竖直管段与弧形管道长度之和，m；L3为物理模型中下行管竖直管段、弧形管段与水平管段长度之和，m；TL1，TL2，TL3分别为从入口起至L1，L2，L3长度后的流体温度，℃；rL为物理模型中水平管与下行管之间圆弧连接的半径，m；Lh为圆弧连接段之后与上行管之间水平管的长度，m；Lm为管道总长，m。

当τ≥0，rb≤r≤rbd，L=0时，T（r，L，τ）为岩土体地表温度边界条件，当τ≥0，rb≤r≤rbd，L=Lm时，T（r，L，τ）为岩土体地底温度边界条件，当τ≥0，rb=rbd，T（r，L，τ）为岩土体径向换热远边界温度边界条件。

3.4 模拟结果比较

为了便于比较，A～D 4组模型依然以坐标变换比例β=1.2、rc=rb、径向节点数N=35、轴向步长dz=20 m、时间步长dt=180 s为基准进行计算，其它参数按表1执行，模拟结果见表7。

表7 不同几何模型的数值计算结果Table 7 Numerical results of different geometric models

由表7可知，模型A，B循环水温度数值计算结果在水平管出口及上行管出口相差小于0.01℃，说明拐点附近热扰动在现有条件下对模拟结果的影响确实可以忽略不计。但是在水平管出口处，模型A的循环水温度略低于模型B，而在上行管出口处，模型A的循环水温度略高于模型B。这是因为当存在拐点时，拐点既参加了水平管的计算也参加了垂直管的计算，水平管出口温度处拐点仅参与了水平管部分计算，因此模型A水平管出口温度略低于模型B，但是经过上行管进口拐点计算后，至上行管出口处，循环水温度反而会高于模型B。模型A，B循环水温度数值计算结果在水平管出口及上行管出口处均低于图1模型，相差约0.52℃，结合表1参数，取热量差约为54 kW，约占总体取热量的5%。模型C，D与图1中数值计算模型的模拟结果同样验证了拐点处的热扰动对换热器出口处循环水温度影响可以忽略这一假设，同时与模型A，B的影响趋势一致。

L型井连接处弯曲半径的大小既与钻井工艺及井下地质条件相关，同时影响整个系统的取热性能，因此针对其变化进行了模拟，得出L型井连接段计算弯曲半径依次为150，200，300，400 m时，循环水提取热量依次为1 007.2，1 001.1，983.5，970.5 kW，与图1模型计算所得的循环水提取热量比较依次减少17.5，23.6，41.2，54.2 kW，两种模型取热量差值随着弯曲半径的增加而增加。

4 结论

①中深层地埋管换热器与其周围岩土体的传热数值计算中，当岩土体上边界（表面边界）采用第一类边界条件时，边界温度应选用岩土体恒温层温度作为边界条件；当岩土体上边界（表面边界）采用第三类边界条件时，以中深层恒定热流与表面对流换热系数之比纳入土壤温度场计算是不合适的。岩土体的主要温度变化发生在近管区域。即使随着运行时间的增加，岩土体的换热远边界不断扩大，但是在实验参数下同深度岩土体温度变化的99%始终集中在距离管中心15 m范围内。

②通过一系列模拟计算分析，给出了适当钻井直径下数值计算的基本参数。推荐相近项目的模型研究参数：坐标变换比例β=1.2，轴向步长dz=20 m，时间步长dt=1 200 s，径向远边界rbd=55～65 m；工程设计参数：坐标变换比例β=1.4，轴向步长dz=20 m，时间步长dt=1 200 s，径向远边界rbd=15～20 m。应用数值模型对换热系统关于热干扰假设进行了定量计算，垂直管与水平管连接拐点处的热干扰对换热器出口循环水温度的影响小于0.01℃。

③将中深层U型对接井换热器中L型井部分的圆弧连接段直接投影成垂直井+水平井进行数值计算是不合适的，这直接导致计算管长增加了0.429rL（实验项目增加了172 m）。因此，在实验参数下，针对L型井圆弧连接段以圆柱换热单元等效圆弧换热单元进行数值计算，其计算结果与将其投影成垂直井+水平井的数值计算结果取热量相差54 kW，约占总体取热量的5%，偏差较大。因此当L型井连接处弯曲半径≥200 m时，推荐以几何模型A，B进行中深层地埋管换热器数值计算。