考虑尾流效应的风电场输出功率优化

刘玉山，胡阔海，王灵梅，郭东杰，申戬林

（1.山西大学，山西 太原 030000；2.国家电投山西新能源有限公司，山西 太原 030006）

0 引言

大型风电场存在的尾流效应是影响风电场输出功率的重要因素。有研究表明，尾流效应可能会导致风电场整场输出功率降低10%～20%[1]。针对尾流效应的控制策略主要包括两类，转速-桨距角控制策略[2]和偏航控制策略[3]。文献[4]提出了一种考虑尾流效应的风电场减载出力优化控制方案，采用改进Jensen尾流模型，给出了任意风向的尾流区域划分方法，在满足系统调频需求的前提下，以风电场有功出力最大为目标，对风电场功率分配进行优化。文献[5]基于偏航尾流模型结合粒子群（PSO）算法对风电机组在不利风向下的偏航进行优化控制，但该算法不利于在湍流强度高且风电机组间距较大时的偏航控制。文献[6]以桨距角和叶尖速比作为优化参数进行研究，与传统控制方式相比，风电机组功率提高了0.3%～3.7%，然而其仿真算例仅涉及3台风电机组，存在普适性不足的可能。文献[7]提出了一种模型预测控制策略，在提高风电场整场输出功率的同时，也能减小机组的疲劳载荷。文献[8]通过内点法调节场内各风电机组轴向诱导因子，以此优化并提高整场输出功率。文献[9]在单机最大风能跟踪控制的基础上考虑尾流影响，通过下游风电机组功率输出曲线计算上游风电机组最优控制曲线，在提高整场输出功率的同时，降低了计算的复杂性。由于风电机组尾流控制模型具有高维数、非线性、高耦合等特点，研究中常用的智能优化算法或预测模型算法尽管在一定程度上提高了风电场的输出功率，但未达到更加理想的优化效果。

本文利用激光雷达实验数据验证了改进的Jensen模型的有效性，以轴向诱导因子做为风电机组输出功率模型，建立了风电场输出功率最大化优化模型；针对PSO算法进行改进，利用改进的粒子群（IPSO）算法，以优化模型为目标函数，以轴向诱导因子为优化参数，对每台风电机组的轴向诱导因子进行群体性优化，提高整场输出功率，并对算例进行仿真分析，验证IPSO算法的优化性能。

1 基于激光雷达实测数据的改进Jensen尾流模型验证

1.1 改进的Jensen模型

Jensen模型作为风电机组尾流模型，具有形式简便、鲁棒性强、精度恰当等特点，且适用于平坦地形下的风电机组尾流建模[10]。由质量守恒定律可知：

式中：ρ为空气密度；r0为风轮半径；u为风轮后轮毂处风速；r为尾流半径；v0为来流速度；v为尾流风速。

在Jensen模型中，距离风轮x处的尾流半径的表达式为

式中：k为尾流膨胀系数。

假设功率系数达到贝兹极限，此时u=1/3v0，将式（2）代入式（1），可得Jensen模型表达式为

由于Jensen模型假设的u=1/3v0在大多数情况下无法满足实际情况，根据动量理论，风电机组风轮后轮毂处风速可表示为

将式（2），（4）代入质量守恒公式，可得改进的Jensen模型。

式中：vi为下游机组i的流入风速；CT为风电机组的推力系数。

1.2 基于激光雷达实测数据的尾流模型验证

在山西省某风电场进行激光雷达测风实验。机组轮毂中心高度为70 m，叶轮直径（D）为82 m，且机组处于平坦地势、主风向上游位置，入流风速受其他风电机组尾流影响的可能性较小。采用Zephl 300激光雷达作为固定雷达，用于测量风电机组的入流风速及风向，以Molas B300激光雷达作为移动雷达，用于测量风电机组尾流区域内不同距离的风速及风向。

选择入流风速约为9 m/s和11 m/s，对其尾流区域风速分布情况进行研究。图1为不同风速下垂直高度风速分布曲线。

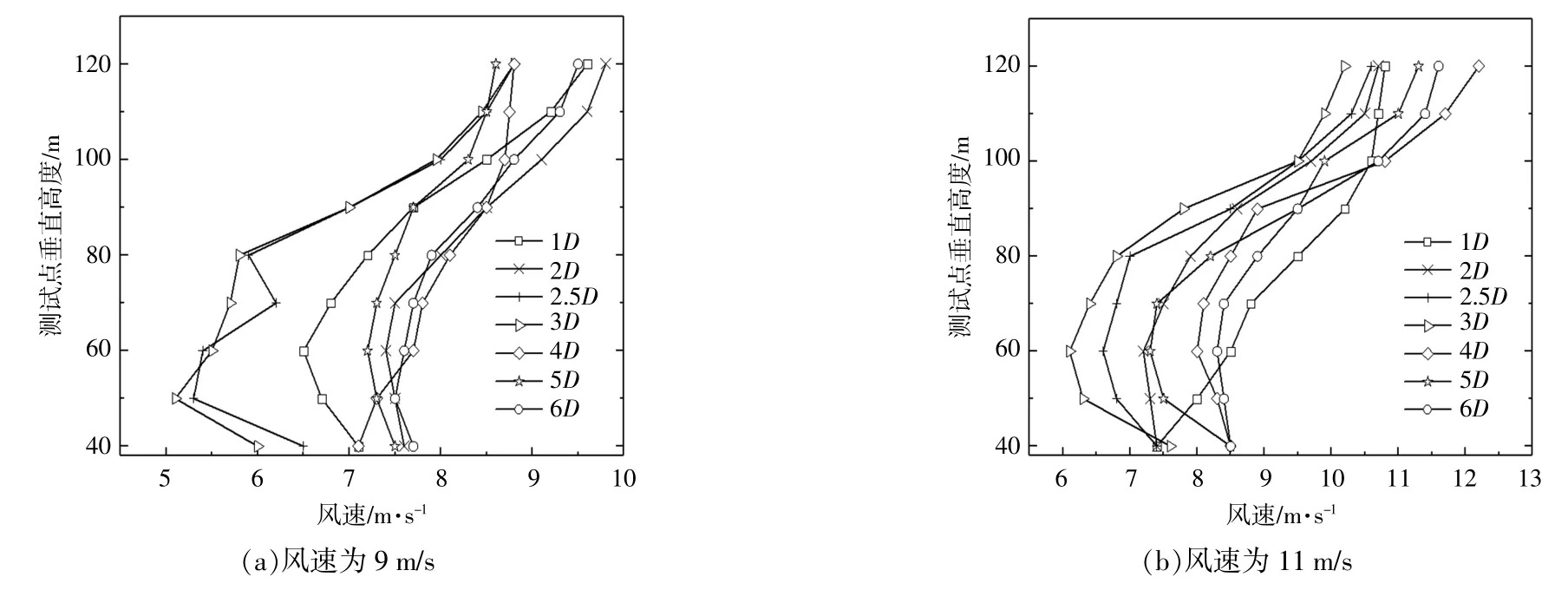
图1 不同风速下垂直高度风速分布曲线Fig.1 Vertical height wind speed distribution curve under different wind speeds

由图1可知：当入流风速为9 m/s时，近尾流区风速减小的程度较大，可能是因为近尾流区受湍流影响较大，风速在垂直高度上的分布整体呈现出先减小后增大的趋势，垂直方向上40～60 m范围内的风速逐渐减小，60～140 m内的风速逐渐恢复；当入流风速为11 m/s时，尾流效应在垂直高度上也明显存在，且近尾流区受尾流影响较大，远尾流区受尾流影响较小。

对来流风速为11 m/s时尾流区域不同距离轮毂高度处的轴向风速进行分析（图2），风电机组轮毂高度处尾流区域风速均有所损失。改进Jensen模型在风机轴向风速上与实测结果拟合程度更高。

图2 实测数据与模型对比图Fig.2 Comparison between measured data and model

根据尾流区域与下游风轮面的覆盖面积的不同，分为全尾流、部分尾流和无尾流。全尾流工况下，尾流区域完全覆盖下游机组风轮面，尾流效应最明显。全尾流工况下，处于下游的第i台风电机组受其上游i-1台机组叠加尾流的影响，其入流风速为

式中：vj为上游第j台风电机组的来流风速。

2 风电场输出功率优化可行性分析

根据空气动力学原理及能量守恒定律，作用在风电机组上的推力T和输出功率P分别为

式中：CP为风能利用系数。

给定风轮直径D为82 m，尾流膨胀系数k为0.075，来流风速为10 m/s，机组间距为6D。图3为尾流风速v与CT的关系曲线。由图3可知，尾流风速随CT的增大而减小，可通过增大上游机组的CT以减小其尾流对下游风电机组的影响。

图3 尾流风速与推力系数关系Fig.3 Relationship between wake wind speed andthrust coefficient

以轴向诱导因子a表示风轮平面风速与来流风速的减少比例。

由式（11）可知，当a=1/3≈0.33时，CP取得最大值CPmax，即贝茨理论极限值0.593。当上游风电机组对风能捕获效率下降超过15%时，将无法弥补下游风电机组的风能损失，因此，CP的下限应是CPmax的85%，可得a的取值为[0.20，0.33]。输出功率P与CT，a之间的关系为

P与CT的关系曲线如图4所示。

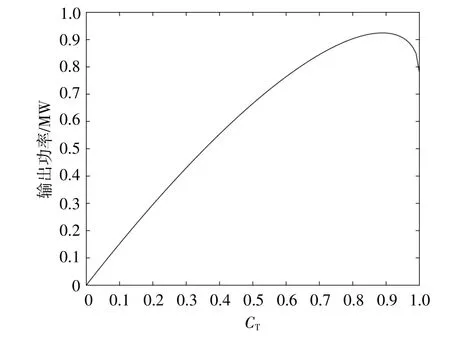
图4 推力系数与输出功率的关系曲线Fig.4 Curve of thrust coefficient and output power

由图4可知，在一定范围内，P随CT的增大而增大，同时尾流风速随a的增大而减小。因此，可以在减小尾流风速与增大输出功率之间寻找一组最佳轴向诱导因子{aii=1，2，…，n}，通过限制上游风电机组的输出功率，减小其尾流对下游机组的影响，从而使整场输出功率最大化。

对于含有n台机组的风电场，其输出功率可表示为

引入尾流模型可得风电场Pall模型为

3 基于改进粒子群算法的风电场尾流优化

3.1 改进粒子群算法

由于风电场输出功率模型具有非线性、高维数、高耦合等特点，标准PSO算法在对其优化的过程中，粒子种群存在多样性不断减小的现象，容易导致目标函数过早地收敛到局部值，致使算法陷入局部最优。因此，在PSO算法的速度迭代方程中加入二阶振荡环节，以此增加粒子多样性，从而提高算法的全局搜索能力。加入二阶振荡环节对于算法前期的搜索能力有了较大提升，使得算法振荡收敛；同时增强了后期的局部搜索能力，使算法渐近收敛[11]。另外，为增强算法的局部搜索能力，本文在此基础上加入了模拟退火算法进行改进，通过给定退火概率，使算法暂时接受较差结果，以此增强局部搜索能力。

PSO算法的迭代方程为

式中：Vi（t+1）为第i个粒子在第t+1次迭代中的速度；Xi（t）为第i个粒子在第t次迭代中的位置；w为惯性权重；c1，c2均为粒子群中的学习因子；pi为第i个粒子在第t次迭代中的最优位置；pg为粒子群在第t次迭代中的最优位置。

在PSO迭代方程的基础上，设φ1=c1r1，φ2=c2r2，则式（18）可表示为

使用二阶振荡环节来替代惯性环节，迭代速度方程可改进为

模拟退火改进方式：给定初始温度Temp，优化过程中Temp会慢慢下降，并产生新的状态，同时会按照一定的概率保留或者抛弃所产生的新状态，最终达到平衡。

为准确、快速了解当地违法猎捕情况，积极与当地乡镇政府、边防派出所协调、沟通，在共同努力下，实现了综合部署、联合巡逻、定点蹲守多措并举，为执法行动提供了有力保障。执法人员不畏山路艰险，经常在凌晨2点到重要林区进行蹲点守候，并不定时到宾馆、饭店、市场、码头等开展突击检查，确保无漏网之鱼。

给定的Temp计算式为

式中：fmax，fmin分别为适应度的最大值和最小值。

通过新旧位置的适应度之差ΔC来判断新位置是否由粒子代替，若ΔC＜0，则粒子进入新位置，否则，需要粒子按照一定概率决定是否保留。决定方式为产生一个（0，1）的随机数rand，若rand＜min [1，exp（-ΔC/T）]，粒子会进入新的位置，并与当前最佳适应度进行比较，最后再进行退温操作。

3.2 优化参数的确定

a的变化会对尾流风速以及输出功率均产生影响，因此将a作为IPSO算法的优化参数。a的调整区间为[0.20，0.33]，对于上游风电机组来说，a的取值越大，意味着其产生的尾流效应越大，对下游机组输出功率的负面影响也越大；减小上游机组的a，意味着其本身的输出功率也会降低，因此，为提高整场输出功率，需要寻找一组a的最优解，以实现风电场整场输出功率最大化。

3.3 优化目标及约束条件

优化目标是使风电场整场的输出功率最大化。目标函数选择为场内所有风电机组输出功率之和。根据式（14）可得目标函数及约束条件为

式中：Pw为风电场整场输出功率；pwi为第i台风电机组输出功率；prate为风电机组额定功率。

4 算例分析

以山西省某风电场为例，机组叶轮半径为41 m，额定功率为1.5 MW，机组间距约为400 m，相关布局如图5所示。以尾流影响最大的270°风向，即全尾流工况为例。取n=5，m=8，风电场内共有40台风电机组。用MATLAB对改进前后的算法进行对比仿真，给定种群数量为150，迭代次数为400。

图5 风电场布局图Fig.5 Wind farm layout

图6为某行机组流入风速优化曲线。

图6 优化前后风速对比Fig.6 Comparison of wind speed before and after optimization

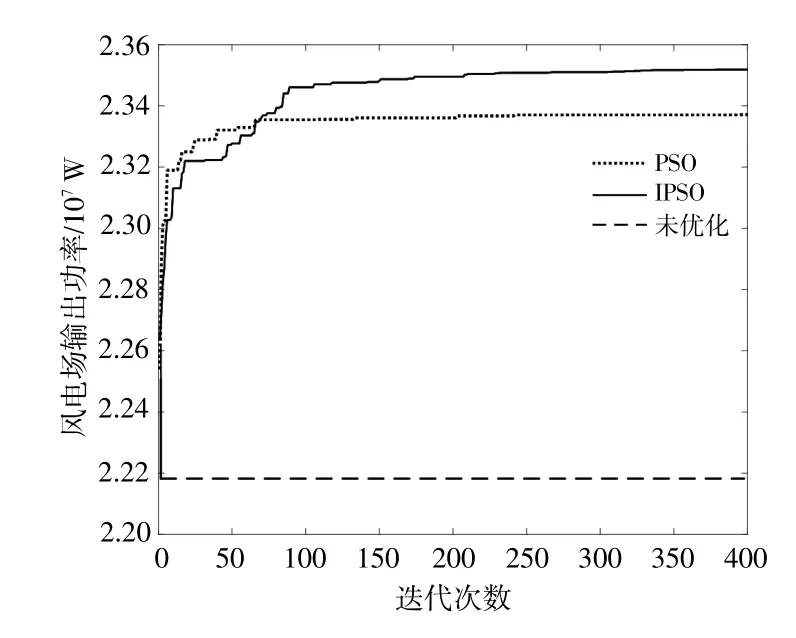
图7 风电机组功率优化曲线Fig.7 Power optimization curve of wind turbines

由图7可知，经IPSO优化之后的输出功率为23.59 MW，较未优化时提高了1.39 MW（6.26%），较PSO优化结果提高了0.22 MW（0.99%）。IPSO算法一定程度上克服了PSO算法过早收敛方面的缺陷，在寻优过程中更有利于寻找到最优值。PSO迭代耗时为18.859 s，IPSO迭代耗时为19.738 s，IPSO迭代耗时能够保证计算速度，满足风电场实时性要求。

表1为风速为8 m/s时的优化结果。第8行数据表示最右列机组的a，由于不存在下游机组，理论上a应为0.33。

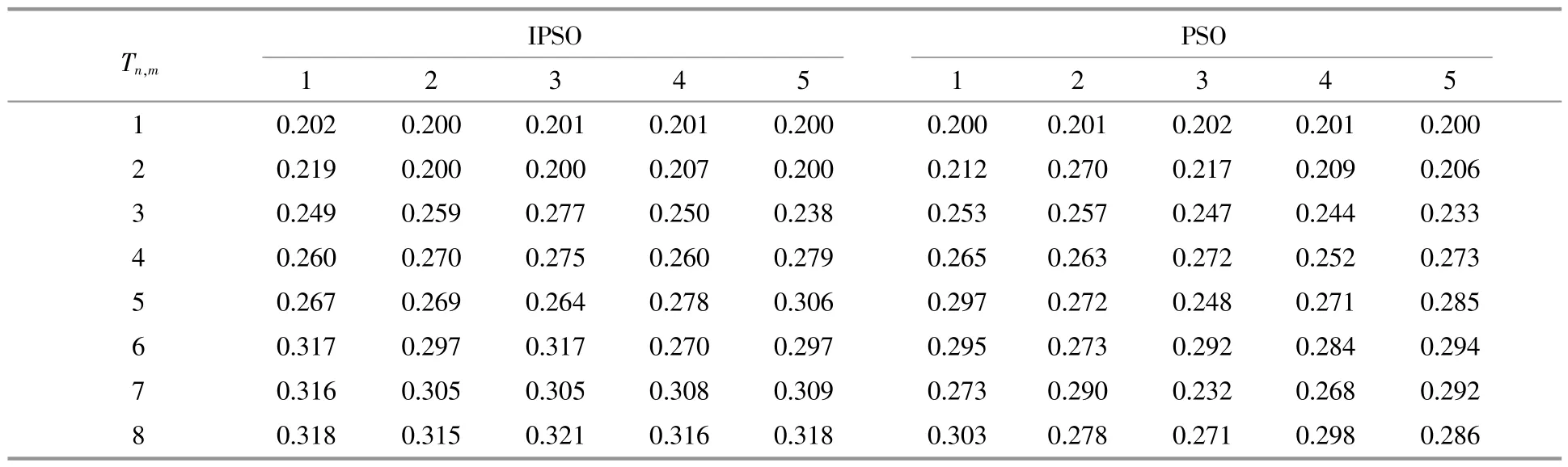
表1 风电机组在不同算法下优化的aiTable 1 Axial induction factor optimized by different algorithms for wind turbines

由表1可知，IPSO算法优化之后的ai更接近理论值，说明IPSO算法优化效果更好，但优化结果与理想值依旧存在一定差距。

图8为风速为12 m/s时，优化前后风电机组的风速。由图8可知，经IPSO算法优化之后的入流风速保持在10 m/s左右。

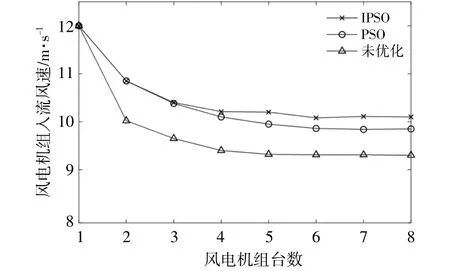
图8 优化前后风速对比Fig.8 Comparison of wind speed before and after optimization

风电场输出功率优化曲线如图9所示。

由图9可知：经IPSO优化之后的输出功率为79.31 MW，较未优化时提高了3.46 MW（4.56%）；经IPSO优化之后的输出功率较PSO算法优化结果提高了0.35 MW（0.46%）。

入流风速为12 m/s时，优化参数的结果如表2所示。

表2 风电机组在不同算法下优化的aiTable 2 Axial induction factor optimized by different algorithms for wind turbines

由表2可知，第8行数据的IPSO算法优化结果更接近于理想值0.33，因此，IPSO算法的优化效果优于PSO算法，但与理想值同样存在一定差距。

5 结论

本文以激光雷达实测数据验证了改进Jensen模型的有效性。建立了风电场输出功率最大化模型，对PSO算法进行改进，利用IPSO算法对风电场输出功率最大化模型进行优化。以山西省某风电场为仿真对象，对来流风速为8 m/s和12 m/s的全尾流工况进行优化，对比分析了IPSO算法与PSO算法的优化性能，得到以下结论。

①当来流风速为8 m/s时，经IPSO算法优化之后的某行风电机组的入流风速均能够保持在6.5 m/s以上，尾流区域内风电机组的入流风速提高了5.13%，IPSO算法优化之后的整场输出功率为23.59 MW，较未优化时提高了6.26%，较PSO算法优化结果提高了0.99%。当来流风速为12 m/s时，经IPSO算法优化之后的某行风电机组的入流风速均能够保持在10 m/s左右，经IPSO算法优化之后的输出功率为79.31 MW，较未优化时提高了4.59%，较PSO算法优化结果提高了0.46%。

②从优化结果来看，IPSO算法能够有效提升风电场输出功率，且一定程度上克服了PSO算法存在的过早收敛、易局部最优等缺陷，具有更好的优化效果。从优化参数的结果对比来看，IPSO算法的优化效果更接近理想值。但由于风电场模型高维数、非线性、多参数耦合的特性，优化结果与理想值依旧存在一定差距。