考虑UFLS响应的大规模风电并网系统频率特性分析

马耀东，刘军福，刘磐龙，雍少华，陈 金，刘财华，周 霞，刘懿诗

（1.国网宁夏电力有限公司 中卫供电公司，宁夏 中卫 755000；2.国电南瑞科技股份有限公司，江苏 南京211106；3.南京邮电大学 先进技术研究院，江苏 南京 210023；4.南京邮电大学 自动化学院 人工智能学院，江苏 南京 210023）

0 引言

随着“双碳”目标的提出，以风电为代表的新能源大规模并网，新型电力系统的发电结构中大量传统同步惯量被取消[1]～[5]。由于风电机组出力具有波动性等特点[6]，加剧了电力系统功率传输的不平衡，增强了电力系统频率波动；另外，源侧、荷侧有功功率轻度不平衡，也使得电力系统频率支撑能力下降[7]。当电力系统出现大规模有功功率缺额时，系统一次调频能力已无法满足有功功率支撑的需求[8]。风电机组联合参与一次调频并采用第三道防线，以防止电网频率发生崩溃。UFLS作为第三道防线的典型控制策略[9]，可快速有效恢复系统频率，从而避免负荷的大规模切除。

风电机组调频策略联合UFLS，成为当前应对电力系统大功率有功扰动的研究热点。文献[10]提出一种转子超速控制策略，分析了双馈风力发电机在长时序扰动下的有功备用调频能力。然而，文献[10]只考虑了风速位于低风速区间的情况。文献[11]，[12]将风机运行区域分为5个部分，并设置桨距角转速目标为额定转速。文献[13]指出，由于机械部件对频率波动突变无法及时响应，因此大多数桨距角控制策略只适合风速大于额定风速的情况。此外，单独使用桨距角控制策略，使得机组频繁动作导致机械磨损[14]。因此，桨距角控制需要与虚拟惯性控制、VSG控制等频率调节策略相结合[15]～[17]。虚拟惯性控制通过模拟同步机组的惯量支撑特性，将频率变化率指标引入频率控制环节，且当电网频率跌落时，附加频率控制将转子动能释放出来调节频率[15]。文献[16]提出虚拟电容以进行虚拟惯性控制，从而利用转子动能提供更多的有功支撑。考虑风电机组转子动能的有限性，研究人员提出了VSG控制策略，采用变流器参与频率控制，通过模拟同步机组的转子特性，从而实现虚拟惯量的支撑[17]。

电力系统受到大功率有功扰动时，单一的风电机组频率控制无法对频率骤降进行有效控制。相关文献对UFLS频率控制策略进行了研究[18]～[20]。文献[18]基于SFR模型并利用经验法验证考虑UFLS方案下的频率特性分析的可行性。文献[19]提出了一种考虑UFLS的多阶系统频率响应模型，定量分析了UFLS控制策略下的频率响应特性。基于所提出的多轮减载方案频率响应模型，文献[20]基于高比例新能源并网的新型电力系统研究背景，提出了UFLS优化方案，分析并对系统频率特性进行优化控制。

上述研究只针对考虑第三道防线UFLS控制策略下的传统电力系统频率特性进行研究，没有考虑当前新能源参与调频的频率控制策略趋势。本文考虑风电机组联合传统火电机组参与调频，并将UFLS方案通过频率响应模型，量化分析了其频率响应控制特性。基于Matlab/Simulink平台对系统频率特征进行仿真，验证本文所提UFLS控制策略的新型电力系统频率特性分析方法的有效性。

1 电力系统频率响应模型

1.1 火电机组频率响应模型

本文基于SFR原理利用低阶线性化模型实现传统火电频率响应控制[21]，模型如图1所示。

图1 火电机组频率响应模型Fig.1 Frequency response model of thermal power

图中：R为一次调频下垂系数；ΔPR为火电机组发电功率增量；FH为原动机高压缸做功系数；TR为再热时间常数；km为机械功率因数；Δf为电力系统频率变化量；s为频域算子。

本文以电力系统频率稳定性为分析目标，不考虑传统电力系统稳定指标中的电压、功角稳定性。传统火电机组附加频率控制环节包括同步涡轮机、调速器控制模块及机械功率增益系数。

1.2 风电机组频率响应模型

当前，风电参与调频的主要方式为有功功率备用控制和转子动能控制。其中，风电机组有功功率备用控制包括超速控制和桨距角控制[10]～[12]，转子动能控制包括惯性控制[15]和VSG控制[16]。

本文以双馈风电机组为例，考虑桨距角控制与转子惯性控制参与风电机组一次调频。风电机组虚拟惯性响应速度较快且持续时间较短，输出的虚拟惯量取决于风机自身惯量、并网同步角速度及惯性响应调频前后的角速度变化。假设频率变化处于死区外且有功变化量处于限幅范围内，当风机经过最大功率跟踪控制，忽略非线性因素，风机惯性响应调频有功变化的线性化特点与同步发电机组的惯性控制类似。因此，采用同步发电机组惯性响应的低阶模型代替风电机组的惯性响应控制[22]。惯性控制调频执行结束后到达高风速区间，桨距角控制调制功率提供风机一次调频。首先，桨距角控制模块接收惯性响应后的转子角速度，并设定为控制模块的角速度参考值。桨距角控制单元负反馈输入的桨距角与经过PI控制及桨距角调节器输出实时风速下的桨距角。风速、桨距角、调速控制后的角速度作为输入量参与双馈风机的功率控制模型，输出该运行工况下的机械转矩。由于桨距角受机械特性影响，该调频控制模块响应时间较长，因此采用常规电源一次调频响应模型代替[23]。

综合二者调频控制工况条件及运行方式可知，当风电场风速处于中风速区间及额定风速区间时，风电机组针对风速改变转子角速度，实现虚拟惯性控制响应；当风电场风速处于高风速区间时，桨距角上升，通过控制桨距角大小以获得机械功率并参与电网一次调频。图2为风电机组频率响应模型。

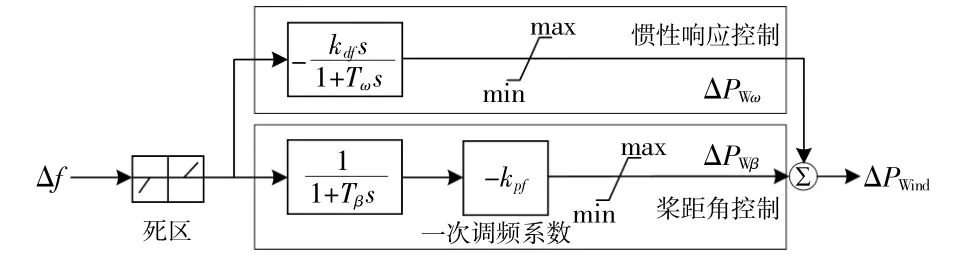
图2 风电频率响应模型Fig.2 Frequency response model of wind farm

图中：Tω为转子惯性响应时间常数；kdf为惯性响应系数；ΔPWω为转子惯性控制的功率变化量；Tβ为变桨距响应时间常数；kpf为一次调频系数；ΔPWβ为变桨距控制提供的功率变化量；ΔPWind为风电发电功率增量。

1.3 UFLS控制频率响应模型

当电力系统受到大功率扰动时，为保证电力系统频率稳定在一定安全范围内，第三道防线进行工作。UFLS作为典型控制方案，对于电力系统大功率扰动后频率稳定调制起到重要作用。电力系统UFLS控制流程如图3所示。图中：ΔPn为UFLS第n轮的频率整定值；Δtn为UFLS第n轮的延时；ΔPLn为UFLS第n轮的切负荷量；ΔPUFLS为UFLS控制单元调频有功功率变化量。

图3 UFLS控制流程Fig.3 The control process of UFLS

1.4 改进的电力系统频率响应模型

电力系统受大功率扰动后，多资源参与调频下的电力系统调频单元提供一定的有功功率支撑。由于考虑UFLS参与频率控制策略，切除部分负荷以减小源荷两端的有功功率不平衡量。通过多调频资源的联合调频及UFLS控制策略实现电力系统大功率有功失衡下的频率稳定调制。参考文献[22]提出的频率控制策略，通过引入调频系数实现各附加频率控制模块的定量有功支撑控制。图4为本文改进的电力系统频率响应模型，考虑火电、风电联合调频，并引入UFLS控制模块。

图4 电力系统频率响应模型Fig.4 Power system frequency response model

为更精确反映电力系统的频率调制动态过程，加入了限幅模块及死区控制模块。图中：ρR，ρWind，ρUFLS分别为传统火电调频系数、风电机组调频系数和UFLS调频单元调频系数；分别为经调频分配后的传统火电、风电机组、UFLS调频单元有功支撑量；ΔPL为电力系统有功扰动大小；ΔP为电力系统有功功率变化量；H为电力系统等效惯性时间常数；D为电力系统等效阻尼常数。

2 大规模风电并网系统参数整定

本文分别对火电机组调频单元、风电机组调频单元及考虑UFLS控制策略下多资源参与调频的电力系统进行参数整定，量化分析电力系统各调频单元的频率响应流程，表征电力系统的频率控制逻辑结构。

2.1 火电机组调频单元参数整定

作为传统同步惯量的主要来源形式，火电机组频率控制模块保留了主要惯量支撑模块，并利用增益系数进行频率响应修正。参考图1所建立的火电机组频率响应模型，根据电力系统频率响应模型传递函数定义，系统频率响应传递函数为有功变化量与频率变化量的比值。火电机组频率响应传递函数为

2.2 风电机组调频单元参数整定

由图2可知，在风电机组频率调制过程中，风电机组功率变化ΔPWind由转子惯性控制的有功变化量ΔPWω和风机变桨距控制有功变化量ΔPWβ两部分组成，从而实现电力系统风电机组一次调频功能。鉴于风电机组转子侧频率响应速度较快，结合其频率相应控制特性，本文采用传统电源的频率响应控制代替风电机组的惯性响应控制。惯性响应控制模块的有功支撑变化量为ΔPWω（s）=-[kdfs/（1+Tωs）]·Δf（s），则风电机组惯性响应控制模块的频率响应传递函数为

考虑到风机转子的机械特性，风机转子无法对源荷两端有功扰动及时响应，采用传统同步机组一次调频控制方式模拟替代风机一次响应能力。以风机变桨距频率控制为例，其控制模块有功功率支撑变化量为ΔPWβ（s）=-[kpf/（1+Tβs）]·Δf（s），则变桨距控制模块频率响应传递函数为

由于考虑风电机组调频控制策略为惯性控制和变桨距控制，风机有功支撑变化量为惯性控制频率变化与变桨距控制频率变化之和，即：

结合式（2）～（4）可得：

风电机组频率响应传递函数为

2.3 UFLS频率控制单元参数整定

在线性化电力系统频率响应模型中，UFLS以延时策略等效实现频率调制作用。参考文献[19]，在系统频率响应模型中加入延时环节，即UFLS频率控制单元有功功率变化量ΔPUFLS（s）=e-τs·Δf（s）。

UFLS频率控制单元频率响应传递函数为

式中：τ为延时时间常数。

2.4 考虑UFLS频率控制策略的电力系统参数整定

本文基于电力系统传统火电机组、风电机组联合调频，并考虑UFLS频率控制策略，量化分析电力系统频率响应特性。由图4可得电力系统频率变化量为

为了精准分配各调频模块的有功调制大小，引入调频系数对调频单元的有功调制大小进行量化控制。当发生有功功率扰动（ΔPL＜0）ΔPL（s）时，定义电力系统频率特性传递函数为频率变化量与有功扰动大小的比值，则电力系统频率特性传递函数为

其中，调频系数满足ρR+ρWind+ρUFLS=1。根据式（9）可得电力系统频率变化量为

调频资源整体频率响应能力由火电机组、风电机组和UFLS频率控制单元组成。调频有功功率变化量为

基于式（12）并利用拉普拉斯逆变换原理，计算得到电力系统频率变化时域表达式为

通过式（13）可计算具体某时间区间下的电力系统频率变化特性，验证系统联合调频的效果，并分析UFLS控制策略的有效性。

根据终值定理可得火电、风电、UFLS控制联合调频下的电力系统稳态频率偏差为

由式（15）可知，电力系统稳态频率偏差与UFLS延时调频控制参数无关，即UFLS频率控制延时时间常数的变化不会影响电力系统稳态频率偏差。

3 算例仿真

本章基于Matlab/Simulink模拟某区域电网采用火电机组、风电机组联合调频，并在大功率扰动下实施第三道防线的单轮UFLS控制策略，电力系统仿真拓扑示意图如图5所示。本文分析不同工况下电力系统的频率特性变化，负荷为1 000 MW，风电额定功率为200 MW，负荷大功率有功扰动为60 MW（0.06 p.u）。

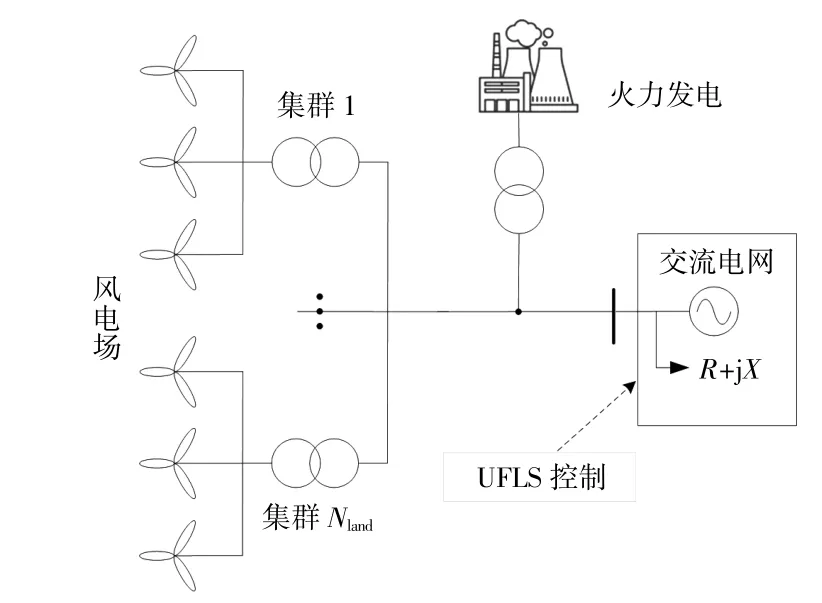
图5 电力系统仿真拓扑示意图Fig.5 Power system simulation topology schematic

3.1 UFLS策略对电力系统频率特性的影响

为验证UFLS频率控制联合多机组调频控制策略的可行性，本节对3种情况下频率特性进行定量分析，考察不同调频方式下电力系统的频率偏差情况。

设置风电场风速恒定且为额定风速，各机组参数如表1所示。

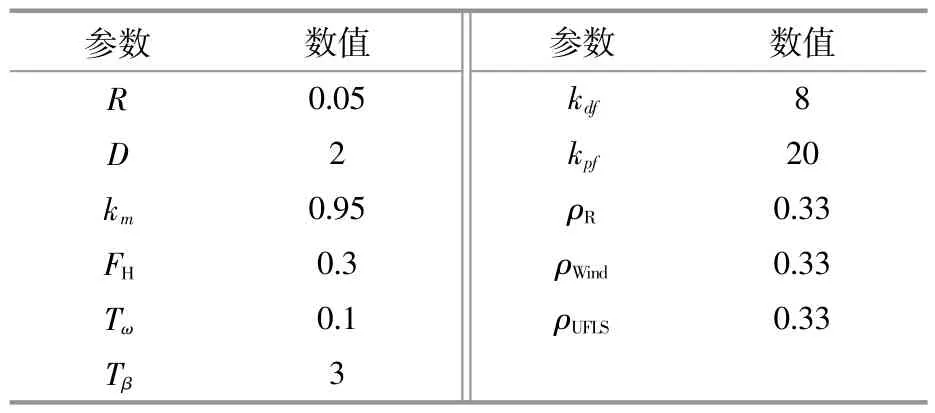
表1 系统参数设定值Table 1 System parameter setting value

分别对火电单独调频、风电参与调频及考虑UFLS 3种调频方式进行仿真，结果如图6所示。

图6 不同调频方式下的电力系统频率曲线Fig.6 Power system frequency curve with different frequency regulation methods

表2 为3种调频方式下的电力系统频率特征仿真结果。

表2 电力系统频率特征仿真值Table 2 Simulated values of power system frequency characteristics

根据图6及表2可知：风电机组调频控制策略的加入使得电力系统频率稳定性提升；基于火电、风电联合调频的控制策略，当实施UFLS频率控制策略时，频率稳定性得到提升；相较于火电、风电联合调频，考虑UFLS策略的调频控制方式下电力系统最大频率偏差绝对值减小0.010 9 Hz，稳态频率偏差绝对值减小0.004 3 Hz。因此，基于风电机组参与调频的控制策略联合UFLS控制策略具有可行性。

3.2 考虑UFLS响应下风电机组有功调制分析

当电力系统受到一定有功扰动时，UFLS调频控制策略可为其提供一定的有功功率。为更加直观地分析风电机组增加的有功功率及UFLS提供的有功功率支撑特性，本文对风电机组及UFLS调频控制单元的有功调制进行仿真，结果如图7所示。

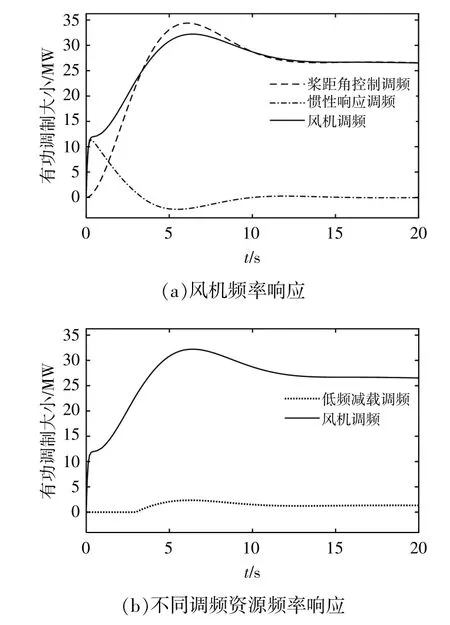
图7 不同调频方式下的电力系统频率曲线Fig.7 Power system frequency curve with different frequency regulation methods

当电网出现有功扰动时，作为调频资源的风电机组及时参与调频作用。由图7（a）可知，风电机组惯性响应控制首先动作，并增加有功功率，在短时间内风电机组提供的有功功率基本为惯性响应调频功率。由于桨距角的机械特性导致频率响应较慢，因此，当惯性响应控制基本结束时，桨距角有功调制为主要调频部分。此时，风电机组提供的有功功率基本为桨距角响应调频功率。由图7（b）可知，当电网出现60 MW的有功功率扰动时，风电机组提供32.21 MW的有功支撑，UFLS提供2.36 MW的有功支撑。因此，UFLS可作为可再生能源高渗透电力系统的辅助调频方式。

3.3 UFLS延时时间常数对电力系统频率稳定性的影响

本节讨论在各调频控制模块调频系数确定时，UFLS控制模块延时时间参数对电力系统频率稳定性的影响。传统火电、风电、UFLS控制参数参考表1，设置UFLS延时时间常数分别为1，2，3 s，考察不同UFLS延时系数下，电力系统最大频率偏差及稳态频率偏差等相关频率稳态指标，如图8所示。

图8 不同延时系数下的电力系统频率曲线Fig.8 Power system frequency curves with different delay factors

表3为电力系统频率特征指标仿真结果。

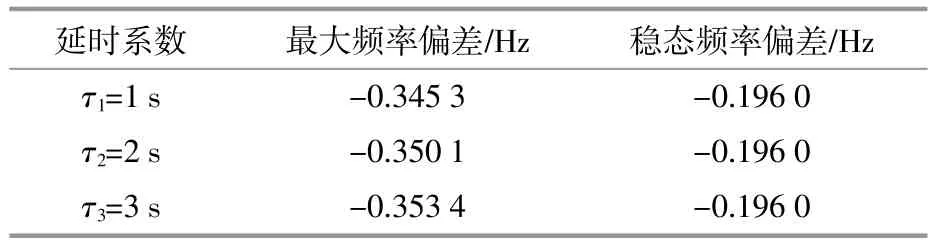
表3 电力系统频率特征仿真值Table 3 Simulated values of power system frequency characteristics

由图8及表3可知，随着延时时间常数的增加，最大频率偏差由-0.345 3 Hz转变为-0.353 4 Hz，频率动态稳定性降低。然而，随着UFLS延时系数的增加，稳态频率偏差不发生变化，即电力系统稳定运行时的频率稳定性与UFLS延时系数无关，与式（15）结论一致。

4 结论

针对新型电力系统受到大功率扰动下的频率稳定性问题，本文提出了一种考虑UFLS频率响应特性的改进的系统频率响应模型。通过仿真验证了UFLS策略联合多资源调频策略下，系统频率特性分析的可行性，结果表明：①改进的系统频率响应模型在经典频率响应模型基础上，增加了风电机组附加频率控制单元及UFLS控制模块，有效反映了大规模风电并网下各调频单元的频率响应特性，及UFLS频率控制单元的响应特性；②大规模风电并网电力系统在受到大功率有功扰动下，考虑风电机组参与调频且联合UFLS频率控制策略下的电力系统频率调制策略，比传统单一火电调频控制模式可提升电力系统频率稳定性，因此计及UFLS的新型电力系统多资源调频控制策略是可行的；③本文所用UFLS控制策略，其频率响应特性本质为对新型电力系统调频控制效果提供延时控制，且电力系统稳态频率偏差与UFLS频率控制延时控制时间常数无关。