考虑风速差异的风电场减载方案与一次调频策略

何廷一，孙领，李胜男，陈亦平，李崇涛，王晨光

(1. 云南电网有限责任公司电力科学研究院,昆明市 650217;2. 西安交通大学电气工程学院,西安市 710049;3. 中国南方电网电力调度控制中心,广州市 510623)

0 引言

风电因具备清洁环保、技术成熟和成本较低等优势,已得到广泛应用[1-2]。 据相关数据显示,截至2020年底,我国风电装机容量占比已达到12.79%,并呈现出较快的增长速度[3]。 而风电机组一般通过变流器接入电网,导致机组转速与电网频率失去耦合关系;且在最大功率追踪(maximum power point tracking, MPPT)控制模式下,风电机组无法在电网频率变化时提供功率支撑作用[4]。 因此随着风电渗透率的增加,惯量降低和一次调频能力不足等问题也在不断突显,给电网频率稳定带来不利因素[5-7]。

为此风电机组应当具备类似于同步机组的惯量响应特性和一次调频能力,以实现风电的友好型并网。 针对该目标,目前采用的方法主要包括转子动能控制和功率备用控制。 转子动能控制分为虚拟惯性控制[8]、下垂控制[9-10]和综合惯性控制[11-14]。 文献[8]较早地提出了虚拟惯性控制的概念,充分利用了风机输出功率可控性高和响应速度快的特点,使得风机能够模拟同步机组的惯量特性并释放转子动能为电网提供功率支撑。 文献[9]分析了下垂控制对系统频率的影响,并得到了不同风电渗透率下的控制参数取值范围。 文献[10]考虑到风机的转速限值,给出了不同扰动大小下不触发转速保护装置动作的下垂系数取值上限。 而综合惯性控制是虚拟惯性控制和下垂控制的组合,文献[11-14]研究了综合惯性控制对于系统频率的改善效果,指出综合惯性控制在减小频率变化率和最大频率偏差方面发挥着重要作用。

然而转子动能控制的调节时间一般不超过6 s[15],且风机偏离最优运行点后将导致机械功率降低,无法提供稳定的一次调频作用。 为此,可结合功率备用控制来改善风机的调频效果,一般可通过超速减载和变桨距角减载的方式留出备用功率。 文献[16-17]根据风速差异制定了超速和变桨距角减载策略,低风速下的风机仅采用超速法,中风速下的风机采用超速和变桨距角结合的方法,高风速下的风机则采用变桨距角法,然而在减载中各台风机承担相同的减载率,未考虑到不同风速下风机减载能力的差异性。 文献[18]指出风速越低,风机通过超速的方式提供的减载率越大。 文献[19]则根据风速的差异,优先选择低风速下的风机进行超速减载操作,但超速减载的风机均运行于最大转速处,不利于风电场的安全运行。 文献[20]按照转子动能最大化和桨距角总变化量最小化的原则,采用优化模型计算各台风机对应的转速和桨距角,但当风电场内风机数目较多且风速差异性较大时模型维数较高,计算较为困难。 因此,充分考虑机组间风速差异性且易实施的减载方案以及相应的调频策略仍有待于进一步研究。

针对上述问题,本文提出一种风电场减载方案以及相应的一次调频策略。 首先介绍综合惯性控制和桨距角控制的原理,并分析风电场减载运行的必要性。 然后研究不同风速下风机减载能力的差异性并制定风电场内减载功率分配方案。 根据制定的减载方案,提出相应的一次调频策略,以充分利用风电场的调频能力并避免频率的二次跌落。 最后基于Matlab/Simulink 搭建仿真系统模型验证所述减载方案和调频策略的有效性。

1 风机频率响应控制原理

1.1 综合惯性控制原理

风机的能量来源为风力机捕获的风能,依据空气动力学知识,风机的机械功率为:

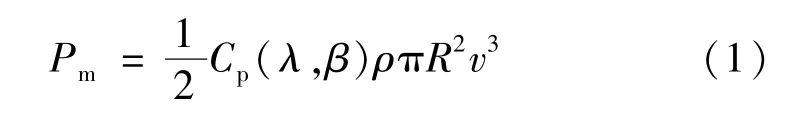
式中:Cp(λ,β)为风能利用系数;λ为叶尖速比;β为桨距角;ρ为空气密度;R为风轮半径;v为风速。

风能利用系数体现了风力机捕获风能的能力,且常用的一种函数表达式为[21]:

式中:ωw为风机转速。

根据不同工况,风机功率曲线如图1 所示,其中风机输出功率参考值Pref的表达式为[22]:

式中:ωmin为风机并网运行的最低转速;ω0为最大功率追踪区的起始转速;ω1为恒转速区的起始转速;ωmax为恒功率区的起始转速;kmax为最大功率追踪系数;Pmax为风机最大输出功率。

在式(3)的基础上,引入综合惯性控制后的控制方程为:

式中:P′ref为引入综合惯性控制后的风机输出功率参考值;kp和kd分别为下垂和惯性系数;Δf为电网频率偏差。

风机功率调整过程如图1 所示,风机初始运行于A 点,当电网频率下降时,风机输出功率参考曲线将上移。 由于转速不能突变,则风机运行点由A 点变化为B 点并向C 点过渡。 因而在暂态过程中,风机可提高输出功率为电网提供短时功率支撑。

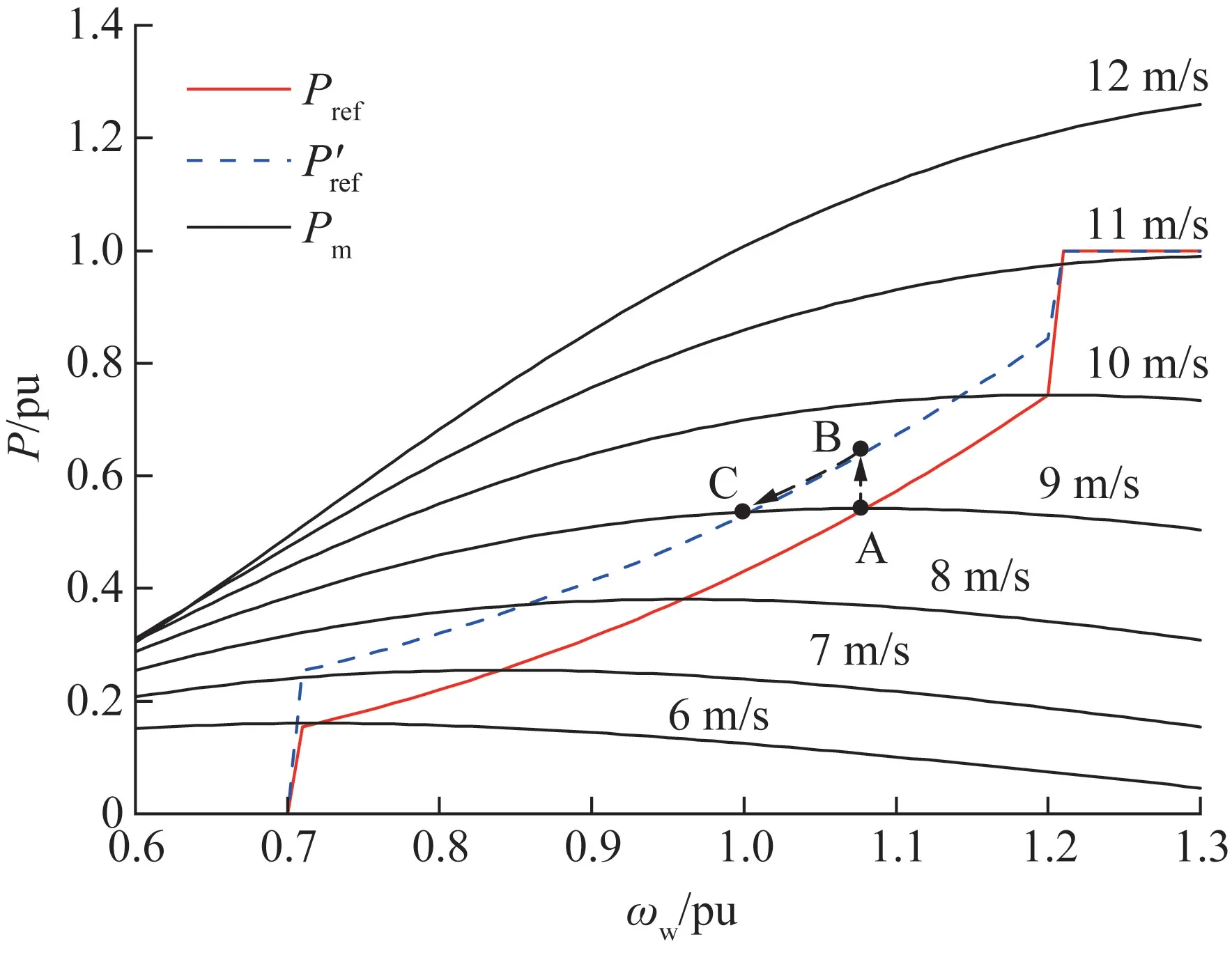
图1 风机功率曲线Fig.1 Power curve of wind turbine

1.2 桨距角控制原理

根据式(1),风机机械功率与桨距角相关,因此可通过改变桨距角来对风机机械功率进行调节,进而改变风机的输出功率。

桨距角控制原理如图2 所示,其中限速模块主要在风速较高的情况下发挥作用,因而在后续分析中忽略限速模块的调节作用。 调频模块的控制方程为:

图2 桨距角控制原理图Fig.2 Schematic diagram of pitch-angle control

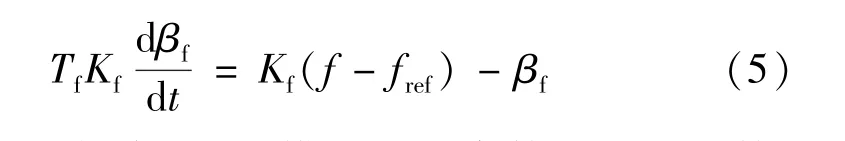
式中:Tf和Kf分别为调频模块时间常数和调节系数;βf为调频模块输出变量;f和fref分别为电网频率和频率参考值。

在电网一次调频结束后,可得:

式中:Δfst= fst-fref,fst为一次调频结束后的稳态频率值。

2 风电场减载方案

以频率下降为例,风机基于综合惯性控制参与电网调频时,由图1 可知,在新平衡点C 处,风机输出功率将低于初始值,因此无法为电网提供持续的功率支撑作用。 而在桨距角控制中,调频模块运作的前提为桨距角须留有调节裕度。 基于上述分析,风机可通过减载运行的方式提高一次调频能力,主要包括超速减载和变桨距角减载等方式。 而单台风机的减载功率有限,因而可从风电场层面制定减载方案。

2.1 超速减载

风机超速减载原理如图3 所示,其中Pref_d为减载后的风机输出功率参考值。 未减载时风机运行于A 点,而B 点和C 点均低于A 点,即为减载运行点。B 点对应超速减载状态,C 点对应减速减载状态。 但C 点为不稳定的平衡点,且减速状态降低了风机存储的转子动能,因而一般选择超速减载状态。

图3 超速减载原理图Fig.3 Schematic diagram of deloading operation by over-speed control

根据式(3),处于最大功率追踪区的风机可实现超速减载运行,此时风机初始转速ωw0满足ω0≤ωw0≤ω1,对应的风速v满足v0≤v≤v1,且v0和v1的表达式为:

式中:λopt为最佳叶尖速比。

风机i最大可超速减载功率的计算式为:

式中:kR= ρπR2/2;vi和βi分别为风机i的风速和桨距角。 则风电场最大可超速减载功率的计算式为:

式中:nm为最大功率追踪区的风机数量。

当调度中心制定的风电场减载功率ΔPfarm满足条件时,风电场仅通过风机超速的方式即可实现减载要求。 此时需将ΔPfarm分配至风电场内各台风机,而当减载功率分配不当时,可能出现部分风机转速升至限值而部分风机转速仍存在较大调节空间的情况,这不利于风电场的安全运行。 为此,考虑到风机风速的差异性,应对不同风机在超速减载方式下的减载能力进行评估,进而确定各台风机的减载功率。

根据式(8),可计算出不同风速下的单台风机最大可超速减载功率,如图4 所示。 由于此时风机桨距角未进行调整,即βi保持为βmin。 为实现风能的有效利用,βmin一般设置为0°,此时也有助于提升基于超速方式实现的减载功率范围。 且在相同桨距角条件下,风速越低,单台风机最大可超速减载功率越大,即减载能力越强。 因此,考虑到不同风机减载能力的差异性,可将风机i对应的减载功率ΔPω,i设置为:

减载后各台风机输出功率参考值可修改为:

式中:ωw,i为风机i的转速;kω,i为风机i超速减载运行时的功率追踪系数。kω,i的计算公式为:

式中:ωws,i为风机i超速减载时的转速运行点。 通过求解ωws,i,即可得到kω,i。

根据式(8)可知,单台风机最大超速减载功率仅与风速相关,则可得到ΔPmaxω,i和vi之间的查找表。 在获取到风电场内各台风机的风速信息后,可结合查找表来计算ks。 而根据式(12),可形成kω,i和vi以及ks之间的查找表。 因此,根据计算得到的ks,可通过查找表来确定kω,i,进而提高计算效率。

2.2 变桨距角减载

当调度中心制定的减载功率ΔPfarm满足条件ΔPfarm＞ΔPmaxω时,可在超速减载的基础上结合变桨距角减载以满足减载要求。 相应的变桨距角减载原理如图5 所示。 图5 中,Pm_d为变桨距角减载运行时的风机机械功率,A 点和D 点为未减载时不同风速下的风机运行点,B 点为超速减载时的风机运行点,C 点和E 点为变桨减载即增大桨距角后的风机运行点。 可见最大功率追踪区、恒转速区和恒功率区的风机可采用变桨距角的方式进一步提高风电场的减载功率。 而据相关统计数据可知,风机输出功率超过自身额定功率80%的概率通常不超过10%[23],即风电场内的风机大多处于最大功率追踪区,因而这里主要分析最大功率追踪区的变桨距角减载方案。

图5 变桨距角减载原理图Fig.5 Schematic diagram of deloading operation by pitch-angle control

由图5 可知,相较于超速减载,变桨距角减载拥有更大的减载范围,因而须对桨距角变化范围加以限制以避免风机输出功率过低。 考虑到变桨距角减载在超速减载达到极限状态后才启动,此时各台风机转速已升至ω1。 则通过增大桨距角以实现变桨距角减载时,风机i的桨距角最大限值βdmax,i为:

式中:βmax为考虑风机机械部分调节能力时的桨距角最大值;β′max,i为考虑功率限制时的桨距角最大值。β′max,i满足:

式中:Pmin,i为风机输出功率限值,其计算式如式(15)所示。

式中:d为风电场减载率,这里取0.3。 式(14)的意义为风机i转速升至限值处的功率高于Pmin,i时,则可进行变桨距角减载,否则不再进行变桨距角减载。

在变桨距角减载中,为了减轻风机机械部分的磨损程度,应尽可能减小风电场内桨距角的总变化量。 类似于超速减载的分析,可对风机在变桨距角减载方式下的减载能力进行评估,进而确定各台风机的桨距角。

为了简化控制操作,在变桨距角减载中,取桨距角单位动作量Δβ为2°。 可设风机i桨距角增加Δβ的次数为nβ,i,则第nβ,i次增加桨距角时的功率变化量ΔPΔβ,i如下所示。

1)当βmin+ nβ,iΔβ - βdmax,i≤0 时,ΔPΔβ,i为:

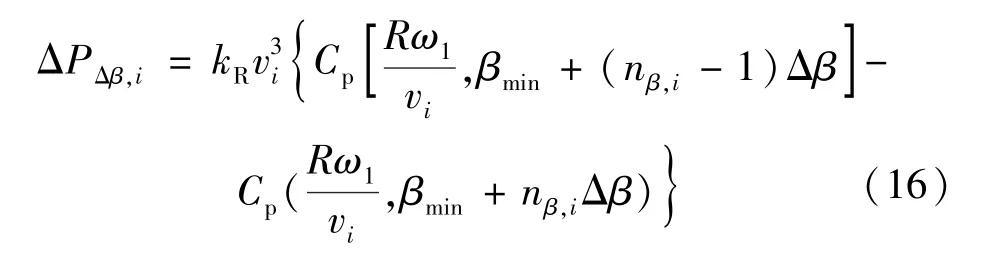
2) 当0＜βmin+ nβ,iΔβ - βdmax,i ＜Δβ时,此时接近桨距角最大限值,则在nβ,i处桨距角增量由Δβ更改为Δβ′i,其表达式为:

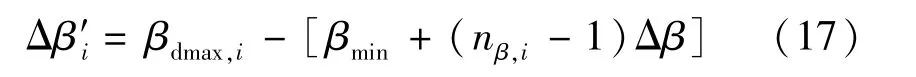
则归算至增量为Δβ下的ΔPΔβ,i为:

3) 当βmin+nβ,iΔβ -βdmax,i≥Δβ时,ΔPΔβ,i为0。

根据式(16)—(18),可得不同风速下ΔPΔβ,i和nβ,i的对应关系,如图6 所示。 可知桨距角增量相同时,风速越高,风机可提供的减载功率越大,即减载能力越强。 因此应优先选择高风速下的风机进行变桨距角减载操作,以减小桨距角的总变化量。

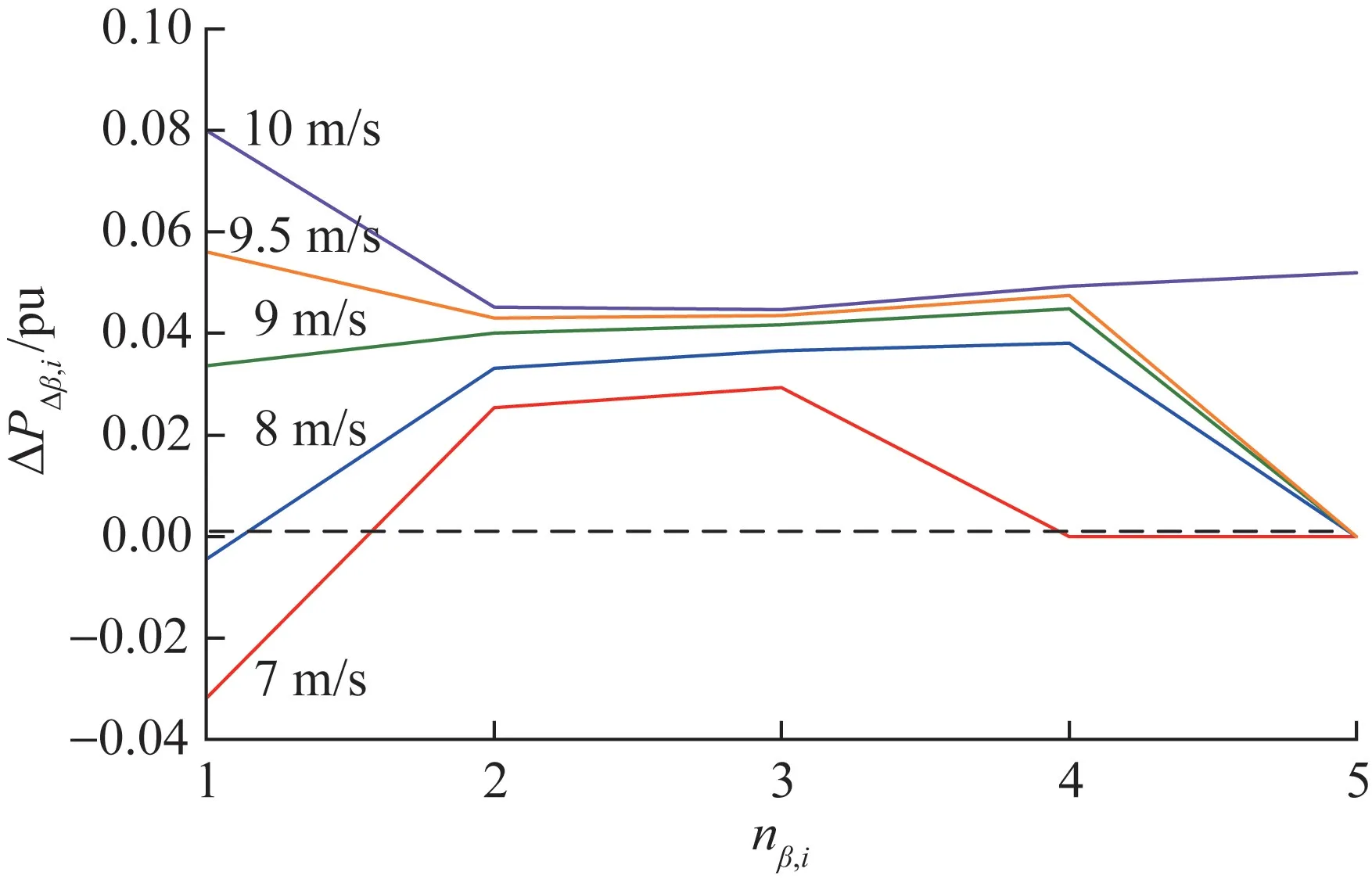
图6 风机功率变化量曲线Fig.6 Power variation curve of wind turbine

基于上述分析,这里将风速按照0.5 m/s 的间隔进行分组。 即根据最大功率追踪区的最高风速v1,将风速划分为(v1-0.5,v1]、(v1-1,v1-0.5]等区间,并按照下述方法进行变桨距角减载操作。

1) 计算所需变桨距角减载的区间数:优先选择高风速区间的风机并计算桨距角增加至限值时的减载功率,若减载功率小于减载要求,则继续选择下一风速区间内的风机进行上述计算,直至累积减载功率大于等于减载要求或各区间内风机桨距角均已增大至限值时停止计算。 后者说明风电场已无法继续减载,对于前者,设得到的所需变桨减载的区间数为m,则此时累积减载功率满足:

式中:mh为第h个区间内的风机数;vh,j和βdmaxh,j分别为第h个区间内第j台风机的风速和桨距角限值。

2) 计算第m个区间内的风机桨距角变化次数:前m-1 个区间内的风机桨距角均增大至限值,第m个区间内的风机桨距角需进行计算。 当该区间内风机桨距角均增加Δβ时,若累积减载功率小于减载要求,则桨距角继续增加Δβ,直至累积减载功率大于等于减载要求,此时可得到该区间内桨距角增加Δβ的次数,并设为b,则此时累积减载功率满足:

式中:ΔP′sum1为式(19)中m更改为m-1 时的计算结果;βbm,j =min{bΔβ,βdmaxm,j} 。

3) 计算第m个区间内第b次桨距角变化中所需变桨的风机数:可知该区间内,第b次桨距角变化中仅需部分风机参与变桨距角即可满足减载要求。 按照风速由高到低的顺序,优先选择高风速风机计算桨距角第b次增加Δβ时的累积减载功率,若仍小于减载要求,则继续选择下一台风机进行计算,直至累积减载功率大于等于减载要求时停止计算。 此时可得到第b次变化中所需变桨距角的风机数,设为n。 在忽略单台风机带来的风电场减载功率与减载要求间的误差时,可将第b次变化中第n台风机桨距角增量选择为Δβ(可增加量不足Δβ时,将其桨距角增至限值即可),则此时累积减载功率满足:

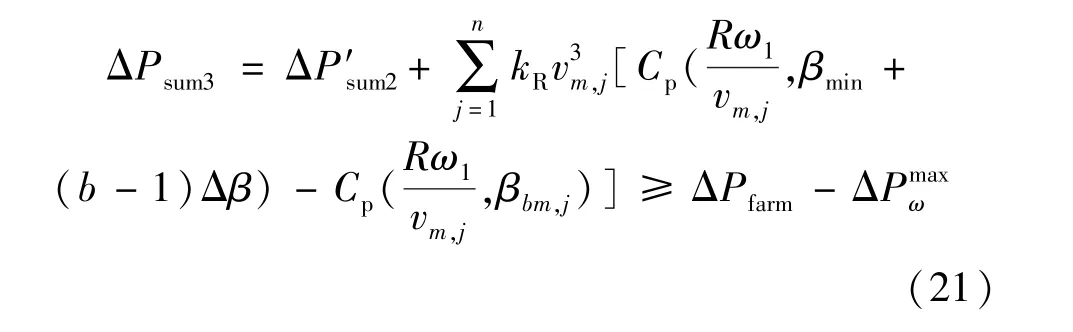
式中:ΔP′sum2为式(20)中b更改为b-1 时的计算结果;βbm,j计算式同式(20)。

由于高风速下的风机优先进行变桨距角减载,因而可减小桨距角总变化量。 且只需通过多项式的计算即可逐步确定各台风机的桨距角,计算过程较为简便。

而变桨距角减载后的风机输出功率参考值可修改为:

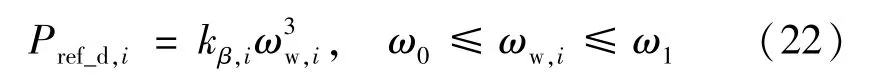
式中:kβ,i为变桨减载运行时的功率追踪系数,其计算式如式(23)所示。

式中:βd,i为变桨距角减载时风机i的桨距角。

3 风电场一次调频策略

由前述分析可知,当ΔPfarm≤ΔPmaxω时,风电场仅采用超速的方式实现减载运行,此时风电场仅通过综合惯性控制参与调频。 结合式(11),式(4)可改写为:

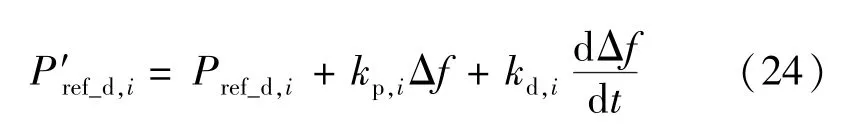
式中:P′ref_d,i为风机i超速减载状态下采用综合惯性控制时的输出功率参考值;kp,i和kd,i分别为风机i的下垂和惯性系数。

由式(10)可知,不同风速下风机的减载功率不相同,风速越低,风机的减载功率越大。 因此,可根据风机的减载情况来确定控制参数,以协调分配风电场的调频功率。 在超速减载状态下,风机功率参考曲线与最大功率追踪曲线之间的功率偏差为:

则可定义功率分配系数ka,i为:

相应的风机i综合惯性控制中kp,i可整定为:

式中:kpf为风电场功率调节系数;Pnf为风电场额定容量;fn为电网额定频率。

综合惯性控制中微分项在扰动初期可抑制频率变化率,而在频率稳定后将不发挥作用,故kd,i可整定为相同值且计算式为[24]:

式中:γ为虚拟惯性系数;Hw为风机的惯性时间常数;Pnw为风机额定容量。

风机基于综合惯性控制参与调频时,转速过低可能导致转速保护动作并带来频率二次跌落问题,因此需对功率调节范围加以限制。 可设风机i综合惯性控制中的附加功率为kv,i,即:

则根据转速限值ω0,附加功率最大限值可设置为:

由此即可避免风机功率调节量过大,同时也不会过度限制风机的调频能力。

当ΔPfarm＞ΔPmaxω时,在超速减载的基础上,风电场还将采用变桨距角的方式实现减载运行。 考虑到桨距角的动作会增加风机的机械磨损程度,因此含有变桨距角减载的风电场一般在出现较大功率扰动时参与调频。 为了充分发挥风电场的调频能力,假设一次调频结束后风机桨距角可恢复至βmin,则根据式(6),风机i桨距角控制中调节系数Kf,i可整定为:

式中:Δfst可根据电网运行经验进行整定,且一般电力系统频率偏差不超过± 0.2 Hz[25], 则可取Δfst= -0.2 Hz。

而变桨距角减载状态下,风机功率参考曲线与最大功率追踪曲线之间的功率偏差为:

则综合惯性控制参数仍可按照式(26)—(28)进行整定。 而在桨距角变化的过程中,附加功率最大限值为:

即附加功率最大限值随着桨距角βi的变化而进行调整,以保证风机转速不会越限。

综合第2 和第3 节的分析,可得控制流程如图7所示。 根据该流程图,即可实现减载功率的协调分配和调频参数的合理设定。

4 仿真分析

基于Matlab/Simulink 搭建了含有风电场的四机两区域系统模型,如图8 所示。 系统中G1—G4 为同步机组,母线10 处接入风电场。 每台同步机组额定容量为900 MW,风电场内各台风机型号相同,额定容量为2 MW,风轮半径R=42 m,风机转速基准值ωn=1.26 rad/s,ωmin=0.70 pu,ω0=0.71 pu,ω1=1.20 pu,ωmax=1.21 pu,最佳叶尖速比λopt=6.33,风机惯性时间常数Hw=5 s。

图8 仿真系统模型Fig.8 Simulation system model

4.1 恒定风速下的仿真分析

4.1.1 场景1:风电场采用超速减载方案

仿真中,风电场内风机信息如表1 所示。 根据式(7),可计算出最大功率追踪区对应的起始风速v0=5.92 m/s,终止风速v1=10 m/s,则表1 中的风机均处于最大功率追踪区。

表1 风电场内风机信息(场景1)Table 1 Wind turbine information in the wind farm(scenario 1)

调度中心制定的ΔPfarm=36.37 MW,而根据表1可计算出风电场最大可超速减载功率ΔPmaxω=73.33 MW,则风电场仅通过超速的方式即可实现减载要求。 根据式(10)可计算出ks=0.50,则各台风机的减载数据如表2 所示。 可见减载功率在不同风机间实现了协调分配,低风速下的风机承担更多的减载功率,以减轻高风速风机的减载压力。

表2 风电场内风机减载数据Table 2 Wind turbine deloading data in the wind farm

为了充分发挥风电场的调频能力,这里取风电场功率调节系数kpf=50。 根据式(25)—(27),可得综合惯性控制中:kp,1= 2.15 ×106,kp,2=2.22 ×106,kp,3=1.05×106。 取γ=10-3,则根据式(28),可得kd,i=2×104。 设系统在20 s 时出现负荷突增扰动,扰动大小为200 MW,这里对3 种控制策略下的仿真结果进行对比分析,3 种控制策略均采用本文所述的减载方案,而在调频策略中有所区别。 策略1:风电场不参与调频;策略2:风电场采用综合惯性控制参与调频,但不考虑式(30)所示的功率限值;策略3:风电场采用综合惯性控制参与调频,并考虑式(30)所示的功率限值。 不同控制策略下的仿真结果如图9 所示。

图9 场景1 中不同控制策略下的仿真结果Fig.9 Simulation results under different control strategies in scenario 1

由图9 可知,在策略1 中,当频率变化时,风电场输出功率未发生改变,无法为系统提供功率支撑。 在策略2 中,由于未考虑附加功率的调节范围,风机转子动能释放较多,进而引发转速保护装置动作。 此时风机将切除综合惯性控制,因而风电场输出功率会大幅下降,并恢复至调频前的功率值。 风电场功率的下降导致了系统频率约在30 s 处再次跌落。 该策略下,为了避免频率的二次跌落,需减小风电场功率调节系数,这将不利于发挥风电场的调频能力。 而相较于策略1,策略3 可有效提高系统频率跌落时的频率最低值,同时也推迟了频率最低值出现的时间,为系统的一次调频提供了更为充裕的时间。 同时,一次调频结束后风电场提升了输出功率,进而提高了稳态时的频率值,且功率增量约为36.21 MW,接近风电场的减载功率,这也说明了式(27)所示的控制参数设定方法的合理性。 相较于策略2,策略3 考虑了附加功率的调节范围,避免了风电场功率调节系数过大导致的频率二次跌落问题,进而可充分利用风电场的减载功率,提升调频效果。

4.1.2 场景2:风电场同时采用超速与变桨距角减载方案

风电场内风机信息如表3 所示,可知各台风机都处于最大功率追踪区。

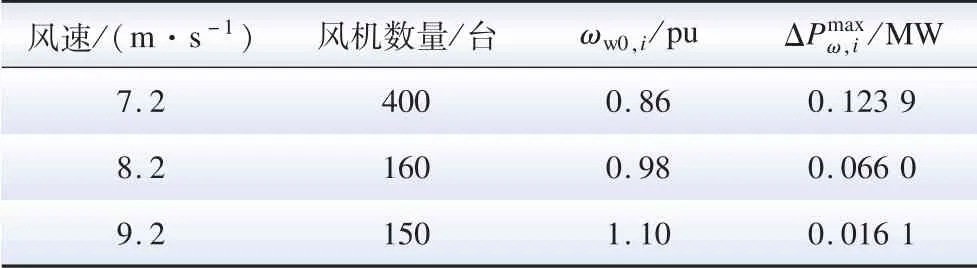
表3 风电场内风机信息(场景2)Table 3 Wind turbine information in the wind farm (scenario 2)

调度中心制定的ΔPfarm=77.03 MW,根据表3可计算出风电场最大可超速减载功率=62.20 MW,因此仅采用超速减载无法满足减载要求,风电场还需采用变桨距角的方式实现减载运行。在变桨距角减载中,这里对2 种变桨距角减载方案进行对比。 方案1:风电场各台风机转速达到最大限值后,在变桨距角减载中,将减载功率平均分配至各台风机;方案2:风电场采用本文所述的减载方案。

通过计算,在方案1 中,7.2 m/s、8.2 m/s 和9.2 m/s对应的风机桨距角分别增加至4.70°、2.48°和0.45°,风电场桨距角总变化量为2342.86°。 在方案2 中,7.2 m/s 和8.2 m/s 风速下的风机无需进行变桨距角操作,桨距角保持为0°;而9.2 m/s 风速下的风机需进行变桨距角操作,其中128 台风机桨距角增加至2°,22 台风机桨距角增加至4°,则风电场桨距角总变化量为344°。 可见在方案2 中,风电场桨距角总变化量显著小于方案1 中的结果。

同样设系统在20 s 时出现负荷突增扰动,扰动大小为200 MW,这里设置3 种控制策略进行对比分析。 策略1:风电场采用上述方案1 实现减载运行,且风电场不参与调频;策略2:风电场采用上述方案1实现减载运行,并按照本文所述的控制策略参与调频;策略3:风电场采用上述方案2 实现减载运行,并按照本文所述的控制策略参与调频。 不同控制策略下的仿真结果如图10 所示。

图10 场景2 中不同控制策略下的仿真结果Fig.10 Simulation results under different control strategies in scenario 2

由图10 可知,相较于风电场不参与调频,风电场基于综合惯性控制和桨距角控制参与调频时可以得到和4.1.1 节算例中类似的结论。 而策略3 中风电场输出功率在30 ～60 s 时间段内高于策略2 中的功率值,原因在于策略3 采用了本文所述的减载方案,平均每台风机对应的桨距角更小,因而风机功率上升更快。 这也使得在系统频率回升阶段,策略3 对应的频率恢复速度略快于策略2 中的恢复速度。 这也说明了本文所述减载方案不仅可减小桨距角总变化量,也可提升风电场的调频效果。

4.2 波动风速下的仿真分析

上述算例为恒定风速下的仿真分析,本节在表1所述风机的基础上引入随机风,分析波动风速下的风机响应情况,仿真结果如图11 所示。

图11(a)中,风速1、风速2 和风速3 分别对应表1 中6.5、8.5、9.5 m/s 的波动风速。 图11(b)和图11(c)中策略1、策略2 和策略3 同4.1.1 节的仿真分析。 可知,在波动风速下,可以得到和4.1 节中类似的结论,风电场仍能表现出较好的调频效果。

图11 波动风速下的仿真结果Fig.11 Simulation results under fluctuant wind speeds

5 结论

针对风电并网带来的惯量降低和一次调频能力不足问题,本文提出了风电场的减载方案和一次调频策略,主要结论如下:

1) 在超速减载中,风机对应的风速越低,最大可超速减载功率越大。 因而本文根据不同风机最大可超速减载功率的差异性,实现了减载功率在不同风机间的协调分配,可有效避免出现部分风机转速升至限值而部分风机仍存在较大调节范围的情况。

2) 在超速减载无法满足减载要求时,风电场可进一步采用变桨距角的方式来满足减载要求。 风速越高,相同桨距角变化量对应的风机功率变化量越大。 因此本文优先选择高风速下的风机进行变桨距角减载操作,且具体步骤简单易行。

3) 考虑到风电场内各台风机的减载情况,本文制定了相应的调频策略,可充分发挥风电场的调频能力,并避免频率二次跌落问题。