虚拟聚合下多微电网功率交互提升配电系统灵活性研究

孙 可，杨 翾，徐祥海，卫 炜，张禄亮，陈佳佳

（1.国网浙江省电力有限公司 浙江华云电力工程设计咨询有限公司，浙江 杭州 310000；2.国网杭州供电公司，浙江 杭州 310016；3.华南理工大学 电力学院，广东 广州 510640；4.山东理工大学 电气与电子工程学院，山东 淄博 255049）

0 引言

在“碳达峰·碳中和”目标下，分布式光伏（Distributed Photovoltaic，DPV）因其资源丰富、环境优化、安全可靠等优点，得到快速发展和广泛应用[1]，[2]。随着DPV在配电网中大规模接入，打破了配电网原有的单相供电模式[3]，DPV输出功率的变化加剧了配电网净负荷功率波动，致使系统灵活性调节资源需求激增，配电设备运行效率低、投资费用高；当灵活性调节资源不足时，容易造成电能质量下降、供电可靠性降低等问题。另外，DPV无序接入极易引起网络堵塞、配电网反调峰问题，不利于配电网整体的经济运行。

储能系统（Energy Storage System，ESS）具有快速响应以及对功率进行双向调节的能力。ESS能够在不同时刻提供充放电服务，将发电峰值时段的电能转移到低谷时期，具有提高可再生能源的就地消纳、缓解网络堵塞、降低配电网净负荷波动等诸多优势[4]，[5]。将ESS和DPV相结合，能够降低大规模DPV接入对配电网运行稳定性的影响，在提高自平衡度、平滑负荷曲线和削减峰值负荷方面发挥积极作用。

DPV和ESS的安装位置和运行方式直接影响配电网可靠运行与灵活性提升[6]。对于节点数目较多的配电网系统，若采用集中式优化方法，会造成系统可靠性降低和运行灵活性不足等问题。因此，对于含有分布式电源的配电网系统，适合采用分区控制方法，即将整个配电网系统虚拟聚合为多个微电网群，每个虚拟微电网实行自治管理，通过对每个微电网的单独控制来实现对整个配电网的能量管理。采用合理的虚拟聚合指标是进行配电网分区控制的前提。文献[7]基于电气距离指标，采用粒子群算法实现电网无功分区。文献[8]基于导纳矩阵参数建立IEEE-39节点系统分区模型，并通过聚类算法求解。文献[9]基于电压稳定指标和网络理论构建分区的内外层，并通过图层叠加，实现无功电压分区。在一定区域内，将配电网虚拟聚合为多个微电网，每个微电网实行自治管理的同时，联合形成互联互供电的集群微电网系统，可以降低系统的运行成本，提高配电网运行的灵活性[10]。灵活性反映了配电网充分统筹和利用系统内可控资源，有效应对运行中的多重不确定性因素扰动并达到供需平衡，适应各种复杂运行环境并维持安全稳定、实现高效经济目标的能力[11]。文献[12]在一定时间尺度内，在考虑灵活性资源的调控成本基础上，通过合理调度节点型和网络型两类灵活性资源，有效应对电源和负荷的波动性和不确定性，使系统同时达到电力平衡和灵活性供需平衡，从而处于一个兼具经济性和灵活性的最优运行状态。上述文献的主要工作集中在虚拟聚合后的功率控制和电压控制，而未考虑配电网虚拟聚合和已聚合形成微电网的功率交互共同作用对配电网运行灵活性的影响。

本文提出了基于虚拟聚合的多微电网功率交互提升配电系统运行灵活性方法，灵活性指标为网络损耗和系统运行成本，在保证电力供需平衡的前提下，降低系统运行成本与网络损耗，同时平滑系统净负荷曲线。首先，综合考虑负荷特性和配电网拓扑结构，提出基于ECS的微电网虚拟聚合方法，将一个配电网虚拟聚合为多个微电网，通过对每个微电网的单独控制来实现对整个配电系统的能量管理与灵活性提升。然后，构建了多微电网功率交互提升系统灵活性模型，提出多目标进化捕 食 策 略 （Multiple Preys-based Evolutionary Predator and Prey Strategy，MPEPPS）求解多目标优化模型，并确定分布式发电机组在虚拟微电网中的最优位置和功率输出。

1 基于电气关联强度的微电网虚拟聚合方法

微电网虚拟聚合是根据空间、功能或结构等综合指标将配电网划分为多个微电网系统。针对配电网虚拟聚合形成微电网问题，本文综合节点的阻抗特性和传输容量，构建基于ECS的虚拟聚合方法，具体描述如下：

对于给定的网络G=（V，L），其中V为节点的数目，L为支路的数目。假设节点间的权重为Wij，则网络的拓扑结构的邻接矩阵A=[aij]可表示为

Newman分区算法能够自动生成最佳分区数目而不需要提前设定[13]，已被广泛应用于电力系统集群划分[10]，[14]。本文采用Newman算法对微电网进行虚拟聚合。假设Cij和Zij分别为节点i和j的传输容量和阻抗参数，本文定义节点间的ECS为ECSij=Cij/Zij。结合邻接矩阵A，网络中节点i的度可表示为ki=∑jAij。若将配电网虚拟聚合为多个微电网，节点i和j分别位于各自的微电网di和dj，则量化参数定义为

式中：若di=dj，则δ（di，dj）=1；否则，δ（di，dj）=0。

结合节点间的ECS函数，节点的度可更新为Ei=∑VjECSij，则配电网虚拟聚合的量化参数为

Qe为配电网中节点间电气关联强度与配电网虚拟聚合形成的微电网中电气关联强度分布概率的差值，其值越大，说明各个虚拟微电网内部节点间电气关联越紧密。因此，通过寻求Qe的最优值，将配电网虚拟聚合为多个微电网，保证每个集群内部节点的电气关联紧密。

2 多微电网功率交互提升系统灵活性模型

在一定区域内，将配电网虚拟聚合为多个微电网，多个相邻的微电网组成一个互联互通的功率交互系统。当某一个微电网存在功率缺额或剩余时，可以安排其他的微电网为该微电网提供能量供应或消纳服务，通过这种方式，能量可在多微电网间共享与互补。多微电网功率交互能够有效利用不同区域多类型资源，发挥能量互济的作用，实现新能源的就地消纳，减少网络堵塞，在提高自平衡度、提升新能源渗透率、平滑负荷曲线、降低峰谷差和削减峰值负荷等方面具有重要意义。

2.1 多目标优化模型

本文构建以支路功率损耗和系统运行费用为灵活性指标的多微电网功率交互提升系统灵活性模型，以确定各个聚合微电网中分布式电源的最优位置和输出功率，进而实现对整个配电网的能量管理。

多目标模型为

式中：Ploss和CDN分别为配电网的功率损耗和运行成本；Pl，Ql，Vl和Rl分别为第i条支路的有功功率、无功功率、电压幅值和电阻；CDPV，CESS，CH和CPS分别为DPV成本、储能系统成本、购电成本及上网收益。

DPV成本由光伏的投资成本和维护成本组成，其表达式为

虚拟微电网中的ESS成本由储能系统的投资成本和维护成本组成，主要由储能系统的使用寿命、单位容量和投资成本等因素组成，即：

功率交互成本为

DPV上网收益为

式中：IPV为DPV单位功率的上网收益。

在多微电网功率交互提升系统灵活性优化模型中，还须考虑功率、电压、储能等运行约束，以确保配电网安全稳定运行，其中功率平衡约束为

式中：Pi和Qi分别为节点i注入的有功功率和无功功率；Ui和Uj为节点的电压幅值；Gij和Bij分别为节点i和j间的支路电导和电纳；θij为节点i和j间的电压相角差。

电压和支路功率约束：

储能系统充放功率及SOC约束：

2.2 虚拟微电网功率交互模型

每个虚拟微电网可等效为一个可调度的发电机，具有双向功率流，并在其整体上进行调度。为避免使用负值变量，定义了4个变量来表示t时刻单个微电网交互的功率：从其他的微电网购电的功率、向其他的微电网售电的功率、从电网购电的功率以及向电网售电的功率。

考虑到虚拟微电网不能同时进行购电和售电，因此，对于单个微电网任意时刻都要满足如下约束：

式中：h和k为虚拟微电网的编号；t为时间变量；T为运行周期；uh，k，t和sh，k，t分别为t时刻微电网h和k进行购电，售电的功率交互状态；αk，t和βk，t分别为微电网与电网进行购电和售电的功率交互状态，若uh，k，t=sh，k，t=0，则微电网h和微电网k不存在功率交互；若仅uh，k，t或sh，k，t等于1，则微电网h和k存在功率交互。若αk，t=βk，t=0，微电网与电网不存在功率交易；若αk，t或βk，t等于1，则微电网k与电网存在功率交互。每个虚拟微电网在同一时刻既可以与其他微电网进行功率交互，又可以与电网进行能量交易[15]。

由于线路容量和逆变器接口的技术限制，交换功率不能超过相应的功率限制。

微电网h从微电网k购电的功率与微电网k向微电网h售电的功率相同。

2.3 灵活性评价指标

为了准确评价基于虚拟聚合的多微电网功率交互提升配电系统的灵活性，本文引入了自平衡度、负荷曲线平滑度、峰谷差和峰补偿4个技术指标。自平衡度函数Zk反映分布式发电对配电网负荷的供应情况以及虚拟微电网间的自治能力，具体参考文献[16]。表征负荷曲线平滑度函数的负荷因子F1、负荷曲线的峰谷差函数F2和净负荷的峰补偿函数F3详见文献[17]，此处不再赘述。

3 算例仿真

为了验证所提模型的性能，在典型的IEEE-33节点测试系统中进行了仿真研究。图1给出了基于虚拟聚合的多微电网功率交互优化模型的流程图，MPEPPS及单目标优化算法EPPS的详细介绍详见文献[17]，[18]。

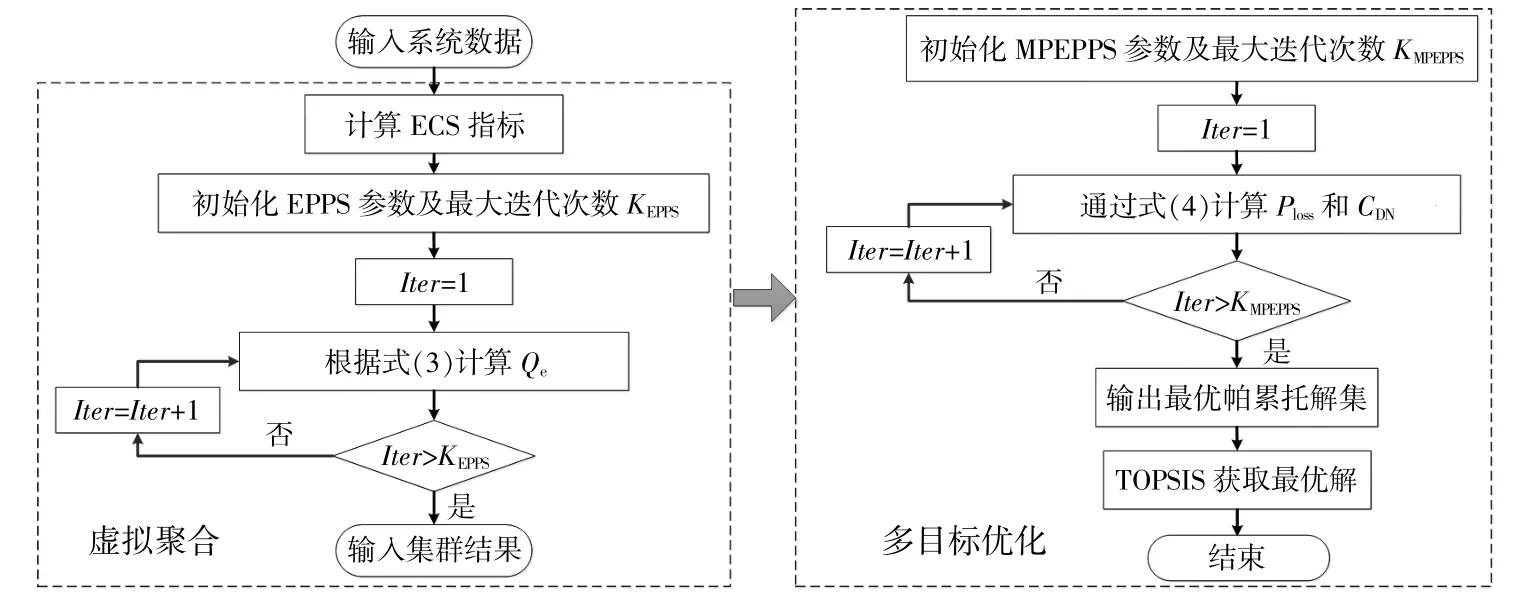
图1 基于虚拟聚合的多微电网功率交互模型流程Fig.1 Flow chart of multi-microgrid power interaction model based on virtual aggregation

本文采用启发式约束处理技术来保证算法更新解满足系统约束条件，该技术描述详见文献[18]，此处不再赘述。IEEE-33节点系统的最大峰值负荷为3 715 kW和2 300 kVar，每小时负荷占峰值负荷的百分比和太阳辐射预测值如图2所示。

图2 日负荷曲线Fig.2 Daily demand curve

本文根据ECS作为虚拟聚合的结构指标，通过EPPS算法得到最优的聚合结果。IEEE-33节点系统虚拟聚合的结果如图3所示。

图3 IEEE-33节点系统划分结果Fig.3 The partition result of IEEE-33 bus system

由图3可知，该系统集群形成4个虚拟微电网，集群1包含节点1，18，19，20和21，集群2包含节点2，3，4，22，23和24，集群3包含节点5～17，25，26，27，28，29，集群4包含节点30，31和32。

当虚拟聚合完成之后，将配电网的划分结果作为优化DG位置的约束条件，通过求解上述多目标优化模型来确定每个集群中DG的安装位置和输出功率。通过MPEPPS算法得到的帕累托前沿如图4所示。横轴和纵轴分别为配电网的运行成本和功率损耗。从图中可以看出，较小的功率损耗将面临较高的运行成本，必须同时考虑配电网的运行成本和功率损耗，以得到最优的DG安装位置和输出功率。

图4 通过MPEPPS得到的最优帕累托前沿Fig.4 The best Pareto front obtained by MPEPPS

通过MPEPPS算法得到帕累托解后，采用多属性决策方法（Technique for Order Ppreference by Similarity Ideal Solution，TOPSIS）获得最优的配置方案。最优解已在图4中标出，最优的运行成本和功率损耗分别为4 919.181 0万元和10 222.84 kW。此外，为验证MPEPPS算法的有效性，表1给出了多目标粒子群算法（Multi-objective Particle Swarm Optimization，MPPSO）[20]和多目标群体搜索算 法 （Multi-objective Group Search Optimizer，MPGSO）[21]在TOPSIS决策算法下的最优结果。值得一提的是，MPPSO和MPGSO的约束处理技术也是参考文献[21]。

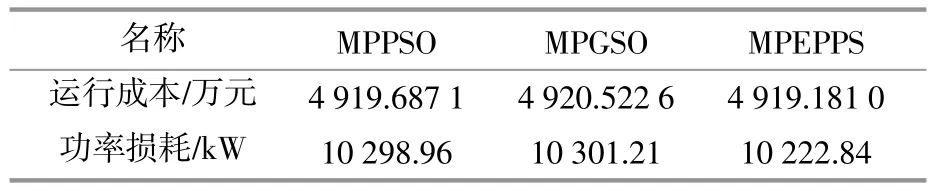
表1 MPPSO，MPGSO和MPEPPS仿真结果Table 1 Simulation results obtained by MPPSO，MPGSO and MPEPPS

由表1可以看出，在求解本文所提模型方面，MPEPPS明显优于MPPSO和MPGSO。

为了评价所提模型的灵活性，引入自平衡度指标。图5显示了考虑虚拟聚合和DG、仅考虑DG和仅考虑虚拟聚合3种情况自平衡度的对比情况。

图5 不同情况下不同集群的自平衡度Fig.5 The self-balance degree of various clusters in different cases

由图5可以看出，本文所提模型的自平衡度大于其他两种情况。这表明对配电网实行分区控制后，促进了DPV的功率输出和集群间的功率交互，减少了从大电网购电的功率，提高了虚拟微电网的自主性。同时，计算了集群间有无功率交互情况下，DPV系统输出功率的情况。当集群间不存在功率交互时，DPV输出功率渗透率为8.34%；当集群间存在功率交互时，DPV输出功率渗透率提高为10.19%。因此，本文所提的多微电网功率交互模型，能有效整合可再生能源，提高可再生能源的渗透率。

每个虚拟微电网中DG最优安装位置分别为节点18，23，6和31（图3）。不同虚拟集群中DPV系统的功率输出如图6所示。

图6 在不同集群中DPV的功率输出Fig.6 The output of DPV in different clusters

由图6可以看出，DPV在1：00-7：00和18：00-00：00没有功率输出，因为这两个时段没有太阳辐射输入，主要通过ESS和购电满足负荷需求。

图7给出了集群1～4中ESS的功率输出。

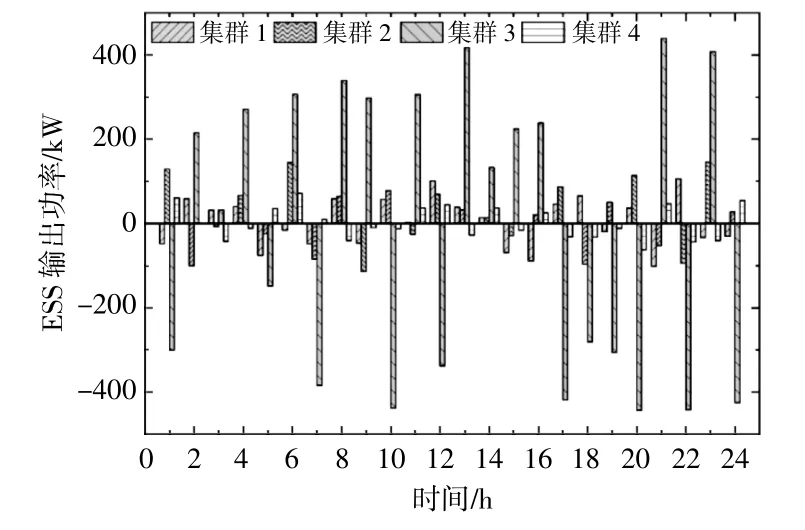
图7 在不同集群中ESS的功率输出Fig.7 The output of ESS in different clusters

由图7可知，集群3中ESS的功率波动较大，而其他集群中ESS的贡献相对均匀，这是因为集群3比其他集群包含更多的节点和负荷，需要ESS更多的功率输出参与功率平衡。

为了定量分析所提模型对净负荷曲线改善的影响，引入了负荷因子F1、峰谷差F2和峰补偿F3，3个指标因子。负荷因子和峰谷差分别用于评价负荷曲线的平滑度和峰谷距离比，峰补偿则为了表明峰值减少的标准化量。表2列出了考虑与不考虑虚拟聚合的负荷曲线特征。表3列出了考虑与不考虑功率交互的负荷曲线特征。

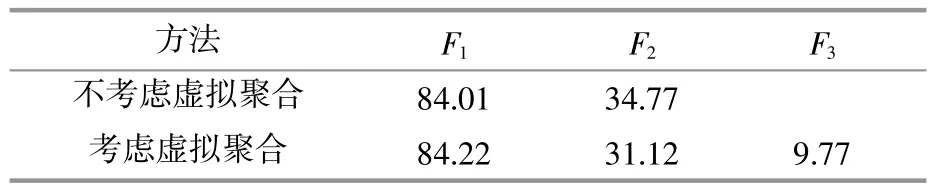
表2 考虑和不考虑虚拟聚合的负荷曲线特征Table 2 Characteristics of the load curve with and without virtual aggregation %

由表2可以看出，考虑虚拟聚合后，净负荷曲线的平滑度由84.01%提高到84.22%，峰谷差由原来的34.77%下降到31.12%。由表3可以看出，考虑功率交互后，净负荷曲线的平滑度由82.23%提高到84.22%，峰谷差由原来的42.34%下降到31.12%，这表明配电网分区控制和集群功率交互能够降低净负荷的波动。同时，分区之后，峰补偿指标为9.77%，集群功率交互后，峰补偿指标为4.53%，这表明配电网分区控制和集群功率交互起到了削峰的效果。

4 结论

为减少大规模DPV接入对配电系统可靠性和经济性的影响，本文提出了一种基于虚拟聚合的多微电网功率交互提升配电系统运行灵活性的方法，并通过MPEPPS算法求解该模型，通过确定最优DG的位置和多微电网交互功率，改善配电系统自平衡度和净负荷曲线，并得出以下结论。①基于ECS指标的虚拟聚合策略，将配电网虚拟聚合为4个微电网群，通过对每个微电网的单独控制，提高了微电网的自主性和配电网的自平衡度，进而促进了配电网的灵活性提升。此外，当微电网群间存在功率交互时，DPV输出功率的渗透率由8.34%提高为10.19%，显著提高了可再生能源的渗透率和就地消纳能力。②构建考虑功率损耗和运行成本的多虚拟微电网交互的优化调度模型，得到了DG在微电网中的最优位置和最优功率输出。配电网分区控制有效改善了净负荷曲线的波动，将净负荷曲线的平滑度由84.01%提高到84.22%，峰谷差由原来的34.77%下降到31.12%，峰补偿提高了9.77%。因此，所提模型在平滑负荷曲线、降低峰谷差和削减峰值负荷方面，实现了配电网的灵活性提升。