浅水圆柱绕流流动模式探讨
李 玲,晏智锋,刘昭伟
(清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
浅水圆柱绕流流动模式探讨
李 玲,晏智锋,刘昭伟
(清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
数值求解了二维浅水方程和RNG k-ε流模型,模拟了不同稳定性系数S和圆柱中心间距G下的单圆柱、两圆柱和三圆柱的尾流流动模式,研究了底部摩擦力对尾流结构的影响。结果表明:随着S增大,尾流在底部摩擦力的作用下趋于稳定,大尺度涡结构逐渐消失。单圆柱尾流区依次出现了涡街(VS)尾流、不稳定漩涡(UB)尾流和稳定漩涡(SB)尾流。多圆柱尾流除了受S数影响外,还与G密切相关。随着G的增大,两圆柱背后依次出现了单钝体绕流、偏转尾流和对称尾流,三圆柱背后则依次出现了单钝体绕流、偏转尾流、对称尾流和非对称尾流。此外,数值结果还表明多圆柱尾流结构不同于单圆柱,多圆柱并排使得尾流更加不稳定。
浅水尾流;流动模式;圆柱绕流;底部摩檫力;圆柱中心间距
1 概 述
浅水尾流的研究主要开始于上世纪80年代,这一现象首先被Scorer[1],Wolanski[2],Pattiaratchi[3],Ingram[4]等人观察到,由于绕流障碍物尺寸一般比较大,他们往往是通过航拍或卫星照片发现这些与深水绕流有着完全不同流动特性的尾流结构。为了对这种尾流进行分类,Wolanski等人提出了岛屿尾流参数P,后来Ingram&chu提出了尾流稳定性参数S,S=CfD/H,其中D,H分别为障碍物横向尺寸和水深,Cf为底部摩擦系数,S反映了底部摩擦力和惯性力之比。可以证明P近似与S成反比。此后学者们对浅水尾流开展了一系列实验研究[5-13]。其中Chen&Jirka[5]在实验室内对各种形状岛屿绕流进行了实验研究,根据不同的S,将岛屿尾流分成3类:涡街(VS)尾流、不稳定漩涡(UB)尾流和稳定漩涡(SB)尾流,并给出了各种流动结构对应的S取值范围。李玲等[11]利用数字图像测速(DPIV)系统对直径为1.27 m的圆柱在浅水层中的尾流流动特性进行了测量,发现流动模式仅取决于稳定性参数S,并给出了合理解释。梁东方等[13]也采用图像测速(DPIV)技术测量了不同形状半岛模型在不同来流条件下的尾流区流速场,得到了控制尾流流动形式的稳定性参数临界范围,分析了半岛尾流近区不稳定流动的机制。在数值实验方面,Furukawa&Wolanski[14]采用离散涡模型discrete vortex model(DVM)对Rattray Island浅水尾流进行模拟。李玲等[15]分别利用Reynolds平均和水深平均的浅水方程对圆柱岛屿绕流进行数值模拟,得出了深水绕流和浅水绕流尾流区分别主要受Re和S影响的结论。Stansby[16]采用三维边界层模型(3DBL)模拟了小坡度圆锥形岛屿的潜水尾流。Stansby[17,18]还分别采用二维(2D)和三维边界层(3DBL)模型模拟圆锥岛屿尾流,分析了平均水深模型的局限性。江春波等[19]也使用平均水深浅水方程模型对平板后面的尾流区进行了数值模拟。在计算过程中,他们采用了3步有限元格式求解浅水方程,且对比了3种紊流模型。多圆柱浅水尾流研究目前还比较少。
本文采用二维浅水方程和平均水深重整化群(RNG)k-ε紊流模型,数值模拟了单圆柱、两圆柱和三圆柱在不同S和G/D下的尾流结构,探讨了浅水圆柱绕流流动模式的变化特征。
2 单圆柱绕流
本文采用了Chen&Jirka[5]实验研究中的模型参数,模拟了4种不同S数下的尾流结构,如图1至图4。
从图中可以看出,S=0.19时,圆柱两边可以看到有规律性的涡街脱落,尾流区形成周期性涡街,可以看到明显的2D大尺度涡结构,形成VS尾流。随着S增加,圆柱两侧有规律性涡脱落开始消失,圆柱背后形成回流,并且区域越来越大,涡街摆动则越来越小。S=0.27,0.34时,紧邻圆柱形成一小段回流区,然后才是尾流摆动,形成了UB尾流。随着S进一步增大,底部摩擦力越来越强,抑制了二维大尺度涡结构的发展,取而代之的是三维涡结构,形成UB尾流。S=0.53圆柱背后即为SB尾流,紧邻圆柱尾流区出现很长的回流区,下游尾流也不再摆动。
更多的模拟工况表明,SV和UB之间的的临界S数约为0.2,UB和SB之间的的临界S数约为0.5,数值结果与试验结果比较吻合。
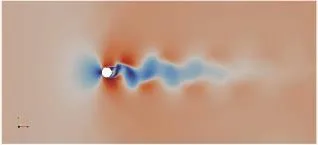
图1 S=0.19单圆柱绕流Fig.1 Flow around isolated cylinder while S=0.19
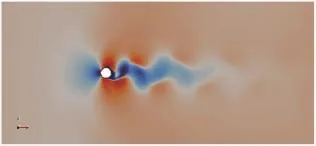
图2 S=0.27单圆柱绕流Fig.2 Flow around isolated cylinder while S=0.27

图3 S=0.34单圆柱绕流Fig.3 Flow around isolated cylinder while S=0.34

图4 S=0.53单圆柱绕流Fig.4 Flow around isolated cylinder when S=0.53
3 两圆柱绕流
本文采用了Huseyin Akilli[20]试验参数,模拟了4种不同的浅水尾流系数S=0.008 2,0.3,0.6,1.0下,G/D=1.125,1.25,2.5圆柱尾流的流态。
3.1 S=0.008 2时的尾流结构
S=0.008 2对应单圆柱涡街尾流,分别给出了G/D=1.125,1.25,2.5对应尾流结构图,如图5至图7。

图5 G/D=1.125和S=0.008 2时尾流结构Fig.5 W ake structure while G/D=1.125 and S=0.008 2

图6 G/D=1.25和S=0.008 2时尾流结构Fig.6 W ake structure while G/D=1.25 and S=0.008 2
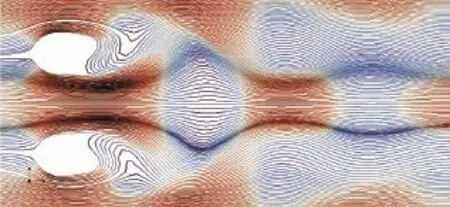
图7 G/D=2.5和S=0.008 2时尾流结构Fig.7 W ake structure while G/D=2.5 and S=0.008 2
图中表明,G/D=1.125时,圆柱下游尾流出现了剧烈的涡街摆动,类似于单圆柱绕流结构,尽管圆柱间隙使得紧邻圆柱的尾流区出现了偏转流,但这种影响非常小,可以忽略。通常把这种圆柱尾流区出现了有规律大幅度摆动的尾流结构称作单钝体绕流。G/D=1.25时,尾流区出现明显偏转,上游流体流过圆柱间隙后向下偏转,挤压下圆柱尾流,使其尾流范围变窄,而上圆柱受到的影响很小,再往下游,上下圆柱尾流合成一股,由于相互作用而摆动大幅度减小,这种尾流被称为偏转尾流。随着G/D增大,尾流趋于稳定。G/D=2.5时,尾流结构关于中心线对称,称为对称尾流。
通过大量的数值计算,发现单钝体绕流、偏转尾流、对称尾流转变的圆柱间距依次大致出现在G/D=1.125,1.8附近。
3.2 S=0.3时的尾流结构
S=0.3对应单圆柱不稳定尾流,给出了G/D=1.125,1.25,1.5对应尾流结构图,见图8至图10。

图8 G/D=1.125和S=0.3时尾流结构Fig.8 W ake structure while G/D=1.125 and S=0.3

图9 G/D=1.25和S=0.3时尾流结构Fig.9 W ake structure while G/D=1.25 and S=0.3

图10 G/D=1.5和S=0.3时尾流结构Fig.10 W ake structure while G/D=1.5 and S=0.3
S=0.3同样出现了单钝体绕流、偏转尾流、对称尾流,只不过出现相应流动结构的G/D比S=0.008 2时要小,这说明S数的增大抑制了两圆柱尾流的不稳定性,尾流区的大尺度涡结构摆动明显变小也说明了这一点。
3.3 S=0.6时的尾流结构
S=0.6对应单圆柱稳定尾流,同样计算了大量G/D对应尾流结构图。结果表明,两圆柱尾流呈现了完全不同于单圆柱的尾流结构,见图11、图12。

图11 G/D=1.125和S=0.6时尾流结构Fig.11 W ake structure while G/D=1.125 and S=0.6

图12 G/D=4.0和S=0.6时尾流结构Fig.12 W ake structure while G/D=4.0 and S=0.6
尾流区同样出现了偏转尾流和对称尾流,对称尾流圆柱后面可以看到明显大尺度涡结构。而单圆柱尾流在S=0.6时已经稳定,尾流区涡摆动完全消失。说明两圆柱并排放置促进了尾流不稳定性发展,使得尾流区出现了大尺度涡结构。
3.4 S=1.0时的尾流结构
当S=1.0时,两圆柱尾流在巨大的底部摩擦作用力抑制下达到稳定,尾流区摆动消失,呈现稳定尾流结构,见图13、图14。

图13 G/D=1.125和S=1.0时尾流结构Fig.13 W ake structure while G/D=1.125 and S=1.0
4 三圆柱绕流
本文采用了Huseyin Akilli试验参数,对不同S和G/D下三圆柱尾流进行数值模拟。由于S=0.3,0.6,1.0时尾流变化规律和两圆柱差别不大,下面只给出S=0.008 2时不同G/D对应的尾流结构,重点考察三圆柱和两圆柱不同之处。
S=0.008 2对应单圆柱涡街尾流,分别给出了G/D=1.125,1.25,2.0,4.0对应尾流结构图,见图15至图18。

图14 G/D=4.0和S=1.0时尾流结构Fig.14 W ake structure while G/D=4.0 and S=1.0

图15 G/D=1.125和S=0.008 2时尾流结构Fig.15 W ake structure while G/D=1.125 and S=0.008 2
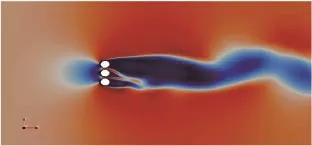
图16 G/D=1.25和S=0.008 2时尾流结构Fig.16 W ake structure while G/D=1.25 and S=0.008 2

图17 G/D=2.0和S=0.008 2时尾流结构Fig.17 W ake structure while G/D=2.0 and S=0.008 2
上述图中表明,随着G/D的增大,尾流结构依次出现单钝体绕流、偏转尾流、对称尾流、非对称尾流。当G/D较小时,尾流为单钝体绕流,下游出现剧烈的涡街摆动。随着G/D增大,尾流开始出现偏转,偏离方圆柱尾流成为主要尾流形式,偏向方圆柱受挤压尾流范围变窄,中间圆柱由于受到上下两圆柱尾流的挤压,尾流范围最小,摆动也最不明显。当G/D进一步增大,尾流呈现对称分布,中圆柱尾流占绝对优势,但是其摆动消失,形成较大回流区。当G/D大到一定程度,尾流对称性消失,呈现非对称尾流,三圆柱摆动周期和幅度都非常接近,只是时间不同步。单钝体绕流、偏转尾流、对称尾流、非对称尾流4种流态转变圆柱间距依次大致出现在G/D=1.2,1.5,2.25附近。
尽管三圆柱尾流具有两圆柱相同的变化过程,但是他们之间又存在很大差异。三圆柱G/D=2.0时便进入对称尾流,与两圆柱对称尾流的分布也完全不一样。但是到了G/D=2.25时又开始出现非对称尾流,说明三圆柱并排放置更不利于尾流稳定。

图18 G/D=4.0和S=0.008 2时尾流结构Fig.18 W ake structure while G/D=4.0 and S=0.008 2
5 结 论
本文采用二维浅水方程模型,数值模拟了不同S和G/D下的单圆柱、两圆柱和三圆柱的尾流结构,得到以下结论:
(1)浅水尾流不同于深水尾流,浅水尾流流动结构由浅水尾流系数S决定,而与雷诺数Re无关。
(2)单圆柱随着S增大依次呈现了涡街尾流、不稳定尾流、稳定尾流,临界值依次为S=0.2,0.5。两圆柱和三圆柱尾流结构不仅与S有关,还与G/D密切相关。随着G/D增大,两圆柱依次出现单钝体绕流、偏转尾流、对称尾流、三圆柱依次出现单钝体绕流、偏转尾流、对称尾流,非对称尾流。不同尾流结构间的临界G/D与S有关,S越大G/D越小。
(3)两圆柱和三圆柱具有与单圆柱不一样的流动特性。当S=0.6时,单圆柱为稳定尾流,两圆柱和三圆柱尾流区出现大尺度涡结构,说明多圆柱排列不利于尾流结构稳定。
[1] SCORER R S.Environmental Aerodynamics[M].New York:Halsted Press,1978.
[2] WOLANSKI E,IMBERGER J,HERON M L.Island wakes in shallow coastalwaters[J].J.Geophys.Res.,1984,89(C6):10553-10569.
[3] PATTIARATCHI C,JAMES A,COLLINS M.Island wakes and headland eddies:A comparison between re-motely sensed data and laboratory experiments[J].J.Geophys.Res,1987,92(C1):783-794.
[4] INGRAIN R G,CHU V H.Flow around islands in Ru-pert Bay:An investigation of the bottom friction effect[J].J.Geophys.Res.,1987,92(C3):14521-14533.
[5] CHEN D,JIRKA G H.Absolute and convective instabili-ties of plane turbulent wakes in a shallow water layer[J].J.Fluid Mech.,1997,338:157-172.
[6] GRUBISIC V,SMITH R B,SCHAR C.The effect of bottom friction on shallow-water flow past an isolated ob-stacle[J].J.Atmos.Sci,1995,52(11):1985-2005
[7] WLOANSKI E,ASAEDA T.Three-dimensional island wakes in the field,laboratory experiments and numerical models[J].Continental Shelf Research,1996,16(11):1437-1452.
[8] LOLYD PM,STANSBY PK.Shallow-water flow around model conical islands of small side slope I:surface pierc-ing[J].J.Hydr.Engrg.,1997,123(12):1057-1067.
[9] BALACHANDAR R,TACHIEM F,CHU V H.Concen-tration profiles in shallow turbulentwakes[J].Journal of Fluids Engineering,1999,121(1):34-44.
[10]JIRKA G H.Large scale flow structures and mixing processes in shallow flows[J].Journal of Hydraulic Re-search,2001,39(6):567-573.
[11]LIL,LIYL,QIXC,et al.Experimental study on flow pattern of cylinder turbulentwake in a shallow-water lay-er[J].Progress in Natural Science,2000,10(6):554-559.
[12]TACHIEM F,BALACHANDAR R.Shallow wakes gen-erated on smooth and rough surfaces[J].Experiments in Fluids,2001,30(4):467-474.
[13]梁东方,李玉梁,陈嘉范.采用DPIV技术研究浅水平板岛屿尾流[J].水科学进展,2004,15(6):711-715.(LIANG Dong-fang,LI Yu-liang,CHEN Jia-fan.Research on shallow plate wake using DPIV[J].Ad-vances in Water Science,2004,15(6):711-715.(in Chinese))
[14]FURUKAWA K,WOLANSKIE.Shallow-water frictional effects in island wakes[J].Estuarine,Coastal and Shelf Science,1998,46(4):599-608.
[15]李 玲,李玉梁.浅水层与深水区圆柱岛屿的近尾流流动[J].清华大学学报(自然科学版),2000,40(8):117-120.(LILing,LIYu-liang.Circular island flow structures in shallow water and deep water[J].Journal of Tsinghua University,2000,40(8):117-120.(in Chinese))
[16]STANSBY PK.Amixing-lengthmodel for shallow turbu-lentwakes[J].J.Fluid Mech.,2003,495:389-384
[17]STANSBY P K.Limitations of depth-averaged modeling for shallow wakes[J].J.Hydr.Engrg.,2006,132(7):737-740.
[18]STANSBY P K.Limitations of depth-averaged modeling of shallow flows with recirculation[C]//Proceedings of the International Workshop on Numerical Modeling of Hydrodynamics for Water Resources-Numerical Mod-eling of Hydrodynamics for Water Resources,Australia:2008:115-126.
[19]JIANG C B,YANG C,LIANG D F.Computation of shallow wakes with the fractional step finite element method[J].Journal of Hydraulic Research,2009,47(1):127.
[20]AKILLIH,AKAR A,KARAKUSC.Flow characteristics of circular cylinders arranged side-by-side in shallow wa-ter[J].Flow Measurement and Instrumentation,2004,15(4):187-197.
(编辑:周晓雁)
W ake Pattern around Cylinder Flow in Shallow-W ater Flow
LILing,YAN Zhi-feng,LIU Zhao-wei
(State Key Laboratory of Hydroscience and Engineering,Tsinghua University,Beijing 100084,China)
The paper numerically investigates flow structures of single,two and multiple cylinders arranged in a shallow water flow.The shallow wakes are simulated with different shallow wake parameters and cylinder center-to-center spacings to investigate the effect of bottom friction and geometry on wake structures.The results show that with the increase of parameter,wakes tend to steady due to the increasing bottom friction,and large-scale vortex structures disappear gradually.Wakes behind multiply cylinders are influenced not only by parameter but also by spacing with the increase of spacing.Vortex streetwake,unsteady vortex wake and steady vortex wake appear be-hind the single cylinder,sequentially.The single blunt body wake,biased and symmetry wakes occur behind two
cylinders,and the single blunt body circumfence,biased wake,symmetry and asymmetry wakes appear behind three cylinders,sequentially.Besides,simulated results indicate thatwake structures ofmultiply cylinders are dif-ferent from that of single cylinder.The arrangement ofmultiply cylindersmakeswakesmore unsteady.
shallow water wake;wake mode;flow around circular cylinder;bottom friction;cylinder center-to-center spacing
TV131
A
1001-5485(2010)10-0030-05
2010-08-23
国家自然科学基金(51079071);水沙科学与水利水电工程国家重点实验室项目(2008-TC-1,2009-TC-2)
李 玲(1970-),女,辽宁沈阳人,副教授,博士,主要从事水力学及河流动力学研究,(电话)010-62782297(电子信箱)li-ling@mail.tsinghua.edu.cn。

