河网模拟JPWSPC方法和分级解法的对比
朱德军,陈永灿,刘昭伟,王智勇
(清华大学水利水电工程系,北京 100084)
河网模拟JPWSPC方法和分级解法的对比
朱德军,陈永灿,刘昭伟,王智勇
(清华大学水利水电工程系,北京 100084)
比较了汊点水位预测-校正法(junction-point water stage prediction and correction,JPWSPC)和经典的分级解法,在处理缓流河网汊点处回流效应时的不同,并对比了它们的计算效率。应用这2类方法时,Saint-Venant方程组都采用Preissmann格式离散,生成的非线性离散方程用Newton-Raphson方法求解。比较表明:这2类方法都能处理普适河网,JPWSPC法无需求解整体连接矩阵,同时不会增加每一时间步的迭代次数,因而节约了系统内存,提高了计算效率;河网中河段数目越多,JPWSPC法的效率优势越明显。
河网水动力数值模拟;汊点水位预测-校正法(JPWSPC);分级解法;效率
1 概 述
隐式差分法稳定性好,能允许较大的时间步长,在一维水动力数值模拟中应用最为广泛,应用隐式差分法离散控制方程后,将形成离散方程组,在每一时间步都需要求解此方程组。单一河道离散方程组的系数矩阵有明显的带状特征,大大节省了计算量。当众多河道相互连接形成河网时,如果流动为缓流,由于回水效应,河网中各分支河道互相影响,必须对河网中的所有支流同时进行模拟[1]。与此同时,河网连接条件破坏了离散矩阵的带状特征,使得求解大型河网系数矩阵所需的内存和计算量都非常巨大。
针对这一问题,诞生了很多处理方法(详见文献[1]和[2]中的综述),其中分级解法[1,3]既能求解树状河网,又能求解环状河网,被大量学者和工程人员采用,尤其在我国,围绕此类方法开展了大量研究,并提出了一系列的改进形式,如三级、四级解法等[4-7]。分级解法主要分为3步:第一步,利用各河网系数矩阵的带状特性,通过消元,建立各河段首末断面变量之间的联系;第二步,将第一步建立的关系与汊点处的连接条件以及外边界条件联合组成整体矩阵,求解此整体矩阵,得到各河段首末断面变量值;第三步:将各河段首末断面的值,代入第一步变换后的系数矩阵,得到所有内节点的变量值。分级解法的第一和第三步利用了系数矩阵的带状特性,第二步中的整体矩阵与整个河网的离散矩阵相比,尺寸大大降低,因而提高了计算效率。
Islam等人[1]曾比较了2种分级解法,我国学者提出的三级和四级等改进解法,都可以建立在这类分级解法之上。但是,吕满英等人[8]发现,当初始误差比较大时分级解法容易失稳。另外,当河网中河段数目很多时,第二步中的矩阵尺寸依然很大,由于该矩阵是不规则的稀疏矩阵,求解相当耗时。文献[2]中,陈永灿和朱德军等人首次提出汊点水位预测校正(JPWSPC)法,利用缓流的特征处理汊点处的回水效应。该方法具有分级解法普适性强的优点,无需建立和求解总体矩阵。本文将JPWSPC法和Islam等人选取的2个分级解法进行对比,重点分析了他们的效率差别。
2 河网控制方程组
河网水动力过程由一维圣维南方程组描述,如方程(1)和(2)所示:

式中:A为过水面积;Q为流量;q为侧向入流量;Z为水位;g为重力加速度;Sf为摩阻坡度,Sf=n2Q|Q|/(A2R4/3),R为水力半径,n为糙率系数。汊点连接条件如(3)、(4)所示:式中下标i和o分别代表流入或流出汊点的河道断面变量值。

3 河网控制方程组数值离散

采用Preissmann隐式差分格式离散方程(1)、(2),并利用Newton-Raphson方法求解离散形成的非线性方程组,得到如下方程:
其中,FC,FM分别表示连续和动量方程,RFC,RFM分别表示其余量,Δ表示连续两个Newton-Raphson迭代步的变量增量。同样,采用Newton-Raphson法求解(3)、(4)得:
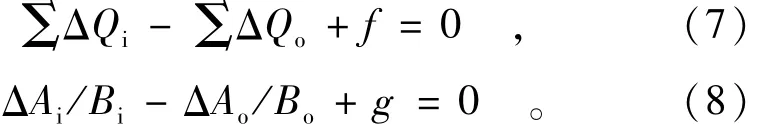
式中:B表示渠道水面宽度;f和g分别表示方程(3)和(4)的左边项的余量。若汊点处有n个分支河道交汇,则有一个形如(7)式的方程和n-1个形如(8)式的方程。由这2个方程可见,因为回水效应,不同分支河道的变量互相联系,河网离散方程组的系数矩阵不再是单一河道的五对角矩阵,这就是用隐式差分法求解缓流河网的难点所在。
单一河道的两端都是外边界,其求解方法已很成熟,而且非本文的重点,故不再赘述。不失一般性,取河段一端是汊点,另一端是外边界的情况进行分析。为了便于比较,本文将各种方法都用系数矩阵的形式表达,方程(5)至(8)以及外边界条件表示成矩阵形式如图1所示。其中EBC和IBC分别表示外和内边界条件,零元素没有标出,#代表非零元素,既可能是零元素也可能是非零元素,可见,在内边界处,系数矩阵的带状特征被破坏。
4 河网处理方法
4.1 Schaffranek等人的方法
该方法由Schaffranek等人于1981年提出(见文献[1]),首先将方程(5)和(6)写成矩阵形式如(9)所示:
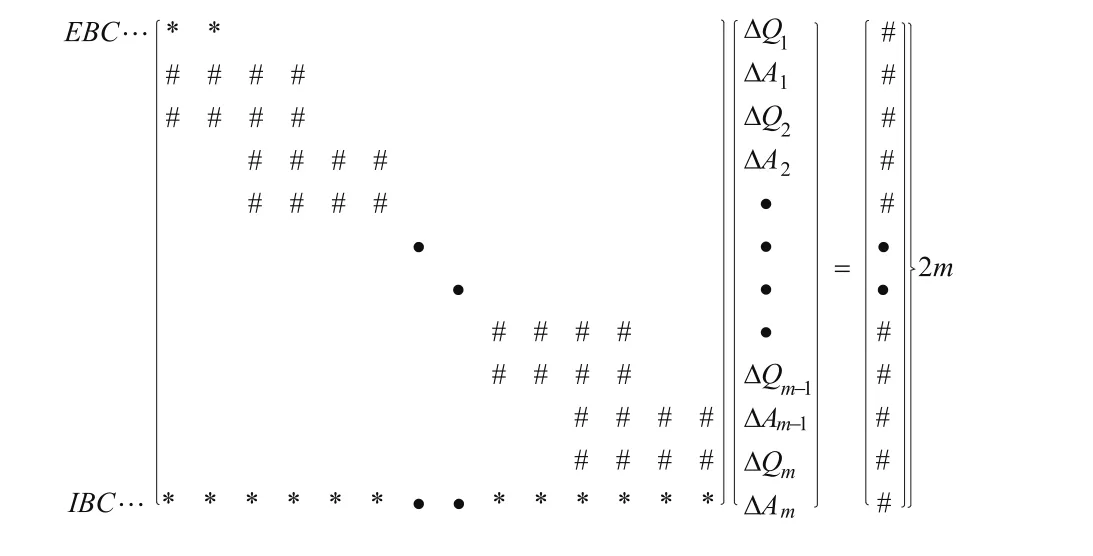
图1 原始系数矩阵示意图Fig.1 O riginal coefficientm atrix

式(9)是一个递归表达式,对各微段(相邻节点间的单元)应用此方程,可得方程

式中:m为河段中的节点数;E1=M1;F1=N1;Ei+1=Mi+1Ei;Fi+1=Mi+1Fi+Ni+1。实际上,由方程(5)和(6)推导方程(10)的过程,等价于将图1所示系数矩阵经过行变换得到图2所示矩阵的过程。图2所示矩阵的第一行,以及最后三行中只含有首尾节点的变量,由此可得整体河段方程组。

图2 Schaffranek等人方法系数矩阵示意图Fig.2 Coefficientmatrix of themethod by Schaffranek et al.
若河网由M个河段组成,则整体方程组的系数矩阵是一个4 M×4 M的稀疏矩阵,常采用高斯消去法求解。如引言中所述,我国学者对河网模拟方法作出了重要贡献,在该类分级解法的基础上,又提出了三级和四级解法,进一步减小了整体矩阵的大小(譬如三级解法通过变换,只保留各河段首尾断面的水位或者流量,将整体矩阵缩小为2 M×2 M)。
4.2 Sen和Garg的方法
Sen和Garg的方法[1,3],其思想与Schaffranek等人的方法类似,也是首先从各河段中,提取出首尾节点的变量,由这些变量组成整体河段方程组,求解河段方程组,然后代入求解各内节点的变量值。不同的是,他们首先由图1所示矩阵,变形为图3所示矩阵,显然前三行和最后一行中只含有首尾节点的变量,由此可得整体河段方程组,同样是一个4 M× 4 M的稀疏矩阵。
4.3 JPWSPC法
上述2种方法处理汊点连接条件时,采用的都是纯粹的数学方法。陈永灿和朱德军等人[2]根据缓流的特征,提出了JPWSPC法,用以处理汊点处的回水效应。根据非恒定渐变缓流的特点,流入和流出汊点断面的流量受汊点水位的影响,若规定流入为正,流出为负,当汊点水位过高时,汊点处净流量为负,反之汊点处净流量为正。根据这一特点,在一次时间步进过程中,首先采用一个预测步,预测各汊点水位,再用若干校正步,使汊点处的条件满足方程(3)和(4)的要求,这就是JPWSPC法。
如图4所示,A点代表一汊点,其坐标为x0,UA和AD分别代表汇于汊点A的两分支河道,水流方向如图中箭头所示,λ+和λ-分别为流经点(x0,t0+Δt)的正负特征线,根据圣维南方程组的性质,在分支河道UA和AD中,水深和流量分别近似满足式(11)和(12)所示关系。

图4 汊点处特征线Fig.4 Characteristic curves at a junction point

根据这2个关系,代入方程(7),可以构造汊点水位的迭代关系,如式(13)所示,
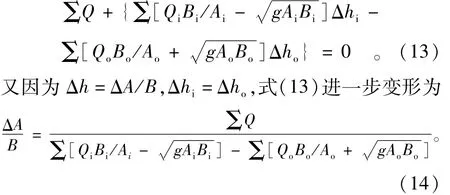
为了简单起见,引入变量AC如式(15)所示,

其中:α为可调整的常数,反映式(11)和(12)推导过程中所作假设的影响,根据经验,α可以取为1.0~2.0,较大的α值有利于计算稳定,较小的α值有利于提高收敛速度。式(14)进一步变形为

将式(16)代入汊点处的内边界条件,图1所示矩阵将变形为图5所示矩阵。

图5 JPWSPC法系数矩阵示意图Fig.5 Coefficientmatrix of the JPWSPC method
这样,通过JPWSPC法,实现了汊点处的解耦,各河段的变量形式上不再互相联系。在每一New-ton-Raphson迭代步,河网的离散矩阵都由彼此独立的五对角矩阵组成,各五对角矩阵可以独立求解。显然,应用JPWSPC方法,求解过程非常简洁,除了将方程(7)和(8)用方程(16)代替外,没有任何额外的步骤,易于程序实现,而且不需要求解不规则的稀疏整体连接矩阵。
5 计算结果及讨论
假想渠网如图6所示,渠道的参数见表1。该渠网既包含树状又包含环状组成渠道,是一个理想的检查河网模拟方法的算例,该算例也曾被Sen和Garg采用[3]。在渠道8-1的外端给定流量条件,其他渠道外边界固定水深为5 m。本研究采用分级解法和JPWSPC方法取得的结果几乎完全一致,所以只画出一条曲线,同时,画出了文献[3]的结果,与本文结果进行比较,由图7可见,结果几乎完全一致。

表1 假想渠网参数[3]Table 1 Parameters of the hypothetic channel network[3]
采用分级解法时,连接矩阵采用选主元高斯消去法求解;所有方法中,采用同样的收敛判据,即|ΔQ/Q|≤0.001和|ΔA/A|≤0.001,同时,采用同样的时间步长Δt=180 s。由图7结果可见,渠道7中产生反方向流动,这一相当复杂的流态,所有的方法都能准确模拟。

图6 假想渠网示意图[3]Fig.6 The hypothetic channel network[3]

表2 各种方法效率对比(应用于图6河网)Table 2 Comparison of the efficiencies of every method used in the network depicted in Fig.6

图7 假想渠网边界条件和计算结果Fig.7 Boundary conditions and calculated results for the hypothetic channel network
为了比较各方法的计算效率和对内存的要求,表2比较了各方法产生的整体连接矩阵尺寸、迭代次数以及模拟时间。结果显示,因为不需要建立整体连接矩阵,JPWSPC法节约了内存,而且减少了每一迭代步的计算时间。表2同时显示,JPWSPC法并不明显增加迭代次数,所以该方法比分级解法快大概28%。
显然,整体连接矩阵的大小,与河网中河段数目有关,河网中河段数目越多,JPWSPC法所节省的内存就越大。为了进一步比较,将河网的节点加密,使微元长度是表1中的一半,相应地,时间步长也缩小一半,Δt=90 s,比较结果如表3所示。表3中的结论与表2类似,JPWSPC法节省了系统内存,减少了模拟时间,同时迭代步数没有明显的增加。表3还显示,因为节点加密,而河段数目不变,JPWSPC法相对分级解法的效率优势有所减弱,比分级解法只快了26%。

表3 各种方法效率对比(应用于加密的图6河网)Table 3 Com parison of the efficiencies of every method used in the refined Fig.6 network
6 结 论
本文比较了最近提出的JPWSPC法和分级解法,在处理缓流河网汊点处回流效应时的表现。比较表明:这2类方法都能处理普适河网,JPWSPC法无需求解整体连接矩阵,同时不会增加每一时间步的迭代次数,因而节省了系统内存,并且提高了计算效率;河网中河段数目越多,JPWSPC法的效率优势越明显。
[1] ISLAM A,RAGHUWANSHI N S,SINGH R,et al.Comparison of gradually varied flow computation algo-rithms for open-channel network[J].J.Irrig.Drain.Eng.,2005,131(5):457-465.
[2] ZHU De-jun.,CHEN Yong-can,WANG Z Y.A novel method for gradually varied subcritical flow simulation in general channel networks[C]∥33rd IAHR Congress.Vancouver,Canada,2009:6327-6335.
[3] SEN D J,GARG N K.Efficient algorithm for gradually varied flows in channel networks[J].J.Irrig.Drain.Eng.,2002,128(6):351-357.
[4] 张二骏,张东生,李 挺.河网非恒定流三级联合算法[J].华东水利学院学报,1982,(1):1-13.(ZHANG Er-jun,ZHANG Dong-sheng,LITing.Three Steps Method to compute unsteady flow for river networks[J].Journal of East China Institute of Water Re-sources,1982,(1):1-13.(in Chinese))
[5] 吴寿红.河网非恒定流四级解算法[J],水利学报,1985,(8):42-50.(WU Shou-hong.Four Steps Method to compute unsteady flow for river networks[J].Journal of Hydraulic Engineering,1985,(8):42-50.(in Chinese))
[6] 侯 玉,卓建民,郑国权.河网非恒定流汊点分组解法[J].水科学进展,1999,10(1):48-52.(HOU Yu,ZHUO Jian-min,ZHENGGuo-quan.Unsteady flow computation using junctions group method in river net-work[J].Advances in Water Science,1999,10(1):48-52.(in Chinese))
[7] 杨开林,白正裕.调水渠网非恒定流的线性变换求解方法[J].水利学报,2004,(3):35-41.(YANG Kai-lin,BAI Zheng-yu.Linear transformation method for calculation of unsteady flow in water diversion net-works[J].Journal of Hydraulic Engineering,2004,(3):35-41.(in Chinese))
[8] 吕满英,江 洧,詹杰民.河网节点水流连接条件处理方法研究[J].人民黄河,2007,29(3):31-32.(LV Man-ying,JIANG Wei,ZHAN Jie-min.Study of treatment for linking conditions at junction points of river networks[J].Yellow River,2007,29(3):31-32.(in Chinese))
(编辑:周晓雁)
Comparison of JPWSPC M ethod and Three-phase Algorithm s for Hydrodynam ic Simulation in General Open-channel Networks
ZHU De-jun,CHEN Yong-can,LIU Zhao-wei,WANG Zhi-yong
(Department of Hydraulic Engineering,Tsinghua University,Beijing 100084,China)
This paper compares a newly proposed method,namely the junction-pointwater stage prediction and cor-rection(JPWSPC)method,for gradually varied subcritical flow simulation in general open-channel networks with conventional three-phase algorithms.Emphasis is on their difference in backwater effect treatment and efficiency.When the two classes of algorithms are implemented,the Saint-Venant equations are discretized using the Preiss-mann scheme and the resulting nonlinear equation system is solved using the Newton-Raphsonmethod.The compar-ison shows that the two classes of methods are applicable in general networks,that,furthermore,the JPWSPC method saves computermemory and computation time by avoiding to establish and solve the globalmatrix without increasing the required number of iterations per time step,and that the advantage of the JPWSPCmethod over the three-phase algorithms increases with increase of the number of junction points.
hydrodynamic simulation in channel networks;junction-point water stage prediction and correction(JPWSPC)method;three-phase algorithms;efficiency
TV131
A
1001-5485(2010)10-0039-05
2010-08-18
国家水体污染控制与治理科技重大专项(2008ZX07207-010-05);国家自然科学基金资助项目(50779026)
朱德军(1980-),男,江苏盐城人,博士后,主要从事水环境和水生态问题研究,(电话)010-62772255(电子信箱)zhudj02@mails.tsinghua.edu.cn。

