基于6σ的零阶差车门系统公差设计

蒋超 肖谦 展若雨 罗健 邝文峰

（蔚来，合肥 230071）

1 前言

汽车对消费者首次视觉冲击表现在汽车的外部形态上，直接影响到消费者的购买意愿，因此汽车的外观品质极其重要。零阶差车门（Flush Door）也称为齐平车门，是指汽车A、B、C 柱与车窗玻璃在没有台阶的连续曲面上，实现一体式镜面效果，同时降低汽车风阻。

与传统车门系统相比，零阶差车门系统中的零件众多，且各零件之间配合相对复杂，传统的公差设计无法满足高面差质量特性的要求，因此需要更加有效的公差设计方法提升零件设计稳健性。

设计试验（Design Of Experiment，DOE）是一种将数学和统计技术相结合，用于建模和分析问题的重要分析方法，是6σ公差设计的重要工具[1]。与传统的单因素法和正交试验法相比，DOE可通过建立影响因素与响应值之间的多元回归方程，明确因素间的交互作用与影响，从而弥补传统试验法无法解释因子之间的交互作用以及不能给出因子和响应之间回归模型的缺陷[2-4]。DOE具有试验次数少、精度高、预测性好的优点，广泛应用于产品稳健性设计以及工艺过程优化等领域[5]。在产品设计早期阶段，应用DOE有利于降低设计成本和缩短开发时间。

许多研究者已经探索了各种各样的公差设计方法，龚鑫等[6]采用极值法与统计公差法，构建尺寸模型，确定了最佳装配方案；Wu 等[7]采用改进的Monte Carlo 方法研究了装配件非线性约束的公差分配方法；还有学者尝试将DOE 与其他方法结合，以提高公差设计的效果[3]。

然而，对于零阶差车门系统的公差设计，目前仍缺乏系统性、有效性的方法。本文研究通过DOE 确定关键零部件与公差，并通过因子的显著性程度来确定公差分配权重优化公差分配，提高产品的合格率和设计的稳健性。同时，本文探讨了零阶差车门系统的设计与制造过程中所面临的挑战，并提出了相应的解决方案。

2 结果与讨论

基于6σ公差设计流程如图1 所示，在零部件开发过程中，DOE 主要体现在确定关键的零部件、估计尺寸链的线性和非线性关系、优化名义值的分配和联合方差权重计划的估计。其中，在确定对封闭环尺寸有显著影响的各组成环公差时，可以采用DOE 模型来进行优化和改进，以确保模型的准确性。同时，需要根据DOE 模型的弯曲显著性来确定是否需要拟合二阶模型，以提高模型的预测精度和准确性。

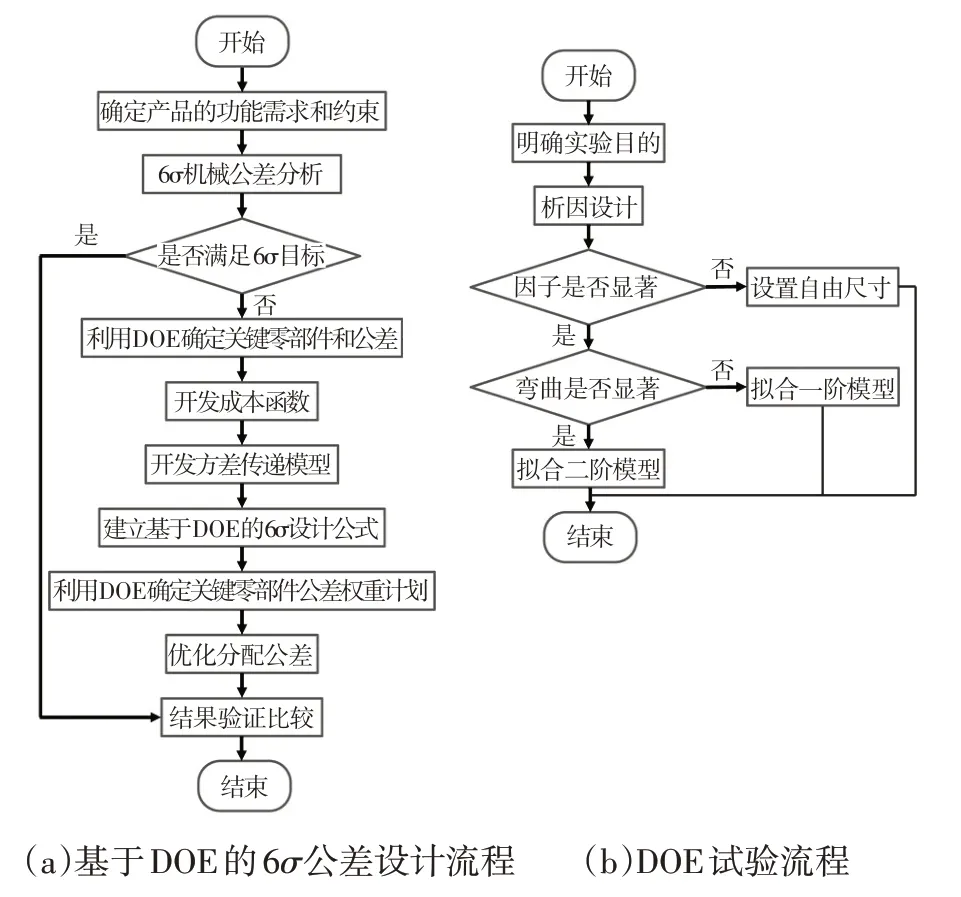
图1 基于DOE的6σ公差设计与试验流程

2.1 DOE模型建立与分析

以前车门为例，零阶差车门系统结构如图2a所示，根据其车门结构设计了如图2b 所示的可调夹具。此工装安装点可根据试验要求，X/Y向任意调节，从而得到不同尺寸状态下的车身工况。

图2 零件总成结构

零阶差车门系统中的关键质量特性为角窗、B 柱饰板与玻璃之间的面差以及玻璃上升时的扭矩，分别代表了车门系统中的外观与功能设计需求，将以上2 个关键质量特性作为DOE 响应变量，记为Y；表1 展示了水切开档变化量、玻璃导轨顶部位置度、角窗位置度、B 柱饰板位置度、玻璃升降器位置度和车门窗框预弯量6 个可能的影响因素，其中正水平代表相对设计位置D0向车外方向移动，负水平代表相对设计位置D0向车内方向移动；采用L64(36)的6 因素、3 水平试验方案对零阶差车门系统影响因素进行试验设计。

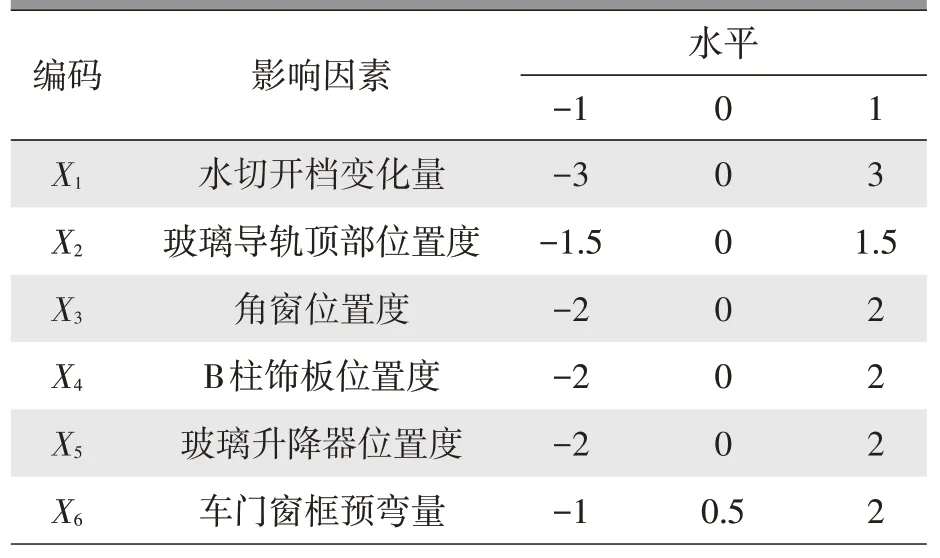
表1 DOE试验因素编码及水平 mm

根据6 因素3 水平的组合设计，其一阶数学模型如下[1]：

式中，β0为常数项；βi为各因子的线性系数；βij为各因子的交互系数；n为变量个数；x为因变量。

利用软件Design Expert 得到67 组试验组合，按此方案进行试验，并测量玻璃面差与玻璃上升时的扭矩，分别以Y1与Y2表示，为了减少试验操作带来的误差，每个响应值测定3 次，结果取其平均值，如表2 所示。

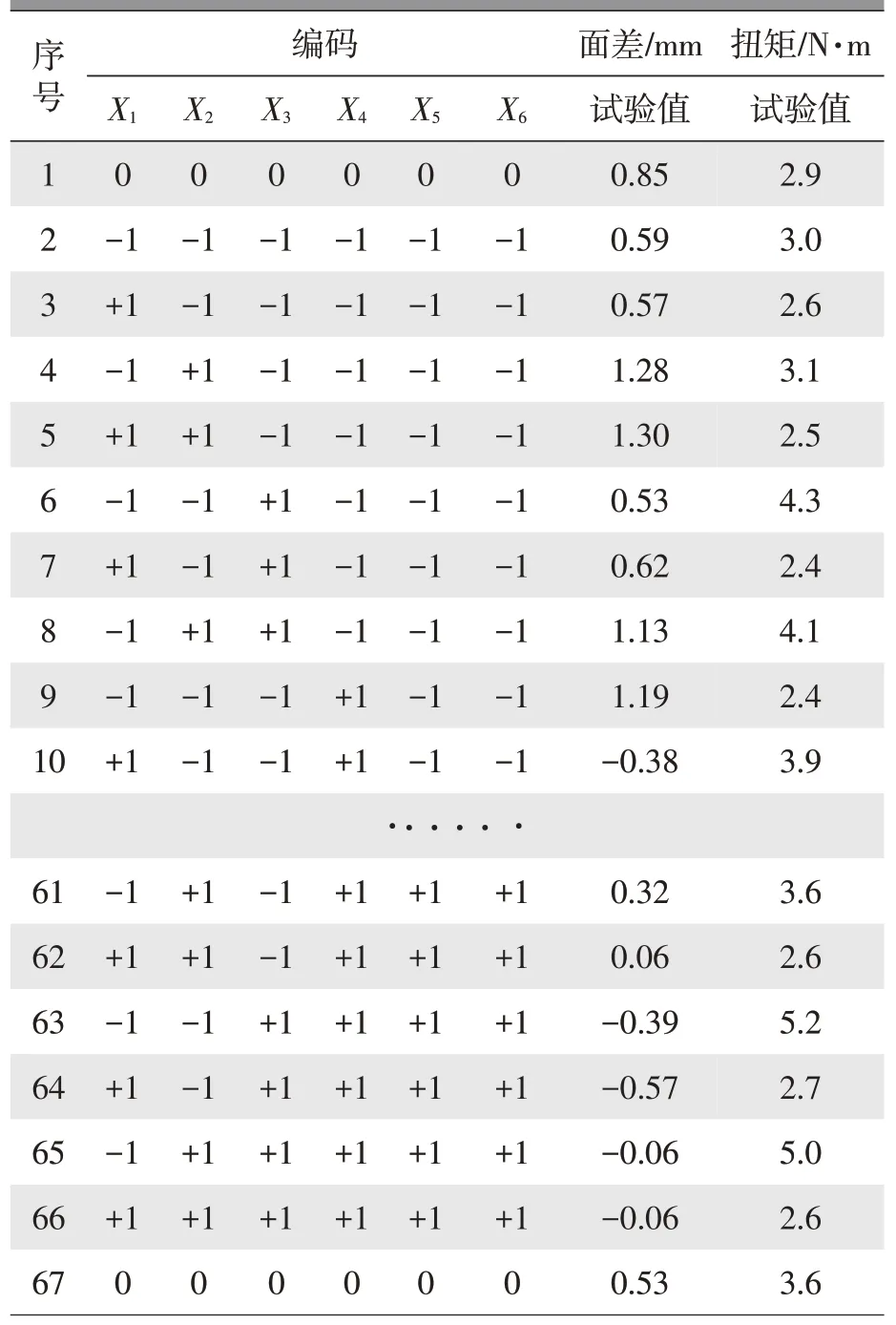
表2 DOE试验设计与结果

对面差与扭矩的试验结果进行方差分析，结果如表3 和表4 所示。模型的显著性用P值（P值为不拒绝原假设的性质）表征。在分析结果中，若P≤0.05，则其为显著项，若P>0.05，则拒绝原假设。

表3 响应变量Y1回归方差分析

表4 响应变量Y2回归方差分析

响应变量Y1与Y2的回归方差分析结果表明，Y1与Y2模型的弯曲项P值均远小于0.05，说明模型显著弯曲，仅用一阶DOE 方程难以精确模拟实际情况，因此需要引入响应曲面分析（Response Surface Methodology，RSM）进一步拟合二阶模型。

2.2 RSM模型分析

响应曲面法一般包括中心复合设计（Central Composite Design，CCD）、中心复合有界设计（Central Composite Inscribed Design，CCI）以及中心复合表面设计（Central Composite Face-centered，CCF）[1]。结合以上DOE 试验结果，本文采用CCF 进行试验。根据CCF 设计，响应曲面数学模型如下[1]：

式中，βii为各因子的二次项系数。

CCF 响应曲面设计及结果如表5 所示，根据其试验结果，对响应变量（面差、扭矩）进行回归方差分析。

表5 CCF响应曲面试验设计及结果

根据Design Expert 软件采用2 次回归模型建立目标函数（面差、扭矩值）与水切开档变化量（X1）、玻璃导轨顶部位置度（X2）、角窗位置度（X3）、B 柱饰板位置度（X4）、玻璃升降器位置度（X5）和车门窗框预弯量（X6）的2 次多项式回归方程，分别如公式（3）和公式（4）所示：

表6 展示了玻璃面差Y1的回归方差分析结果，其中回归模型的F=59.40，模型显著性水平P<0.000 1，说明试验该回归模型有效；失拟项显著性水平P=0.277 8，>0.05，说明失拟项不显著，模型拟合程度较高。在模型的二次项中，玻璃导轨顶部位置度（X2）、B 柱饰板位置度（X4）和车门窗框预弯量（X6）对响应变量Y1有显著影响，其中显著性水平P由小到大为：车门窗框预弯量（X6）、B 柱饰板位置度（X4）、玻璃导轨顶部位置度（X2）。Y1模型的决定系数R2=0.968 6、校正决定系数R2=0.952 3，与预测决定系数R2=0.924 8 均接近1，说明模型Y1具有较强的可靠性和预测精度。

表6 基于RSM响应变量Y1回归方差分析

表7 展示了扭矩Y2的回归方差分析结果，其中回归模型的F=51.42，模型显著性水平P<0.000 1，说明该回归模型是有效的；失拟项显著性水平P=0.996 2，>0.05，说明失拟项不显著，模型拟合程度较高。在模型的一次项中，水切开档变化量（X1）、角窗位置度（X3）、B柱饰板位置度（X4）、玻璃升降器位置度（X5）和车门窗框预弯量（X6）对响应变量（扭矩）有显著影响。Y2模型的决定系数R2=0.963 9、校正决定系数R2=0.945 1和预测决定系数R2=0.922 6均接近1，说明Y2模型具有较强的可靠性和预测精度。

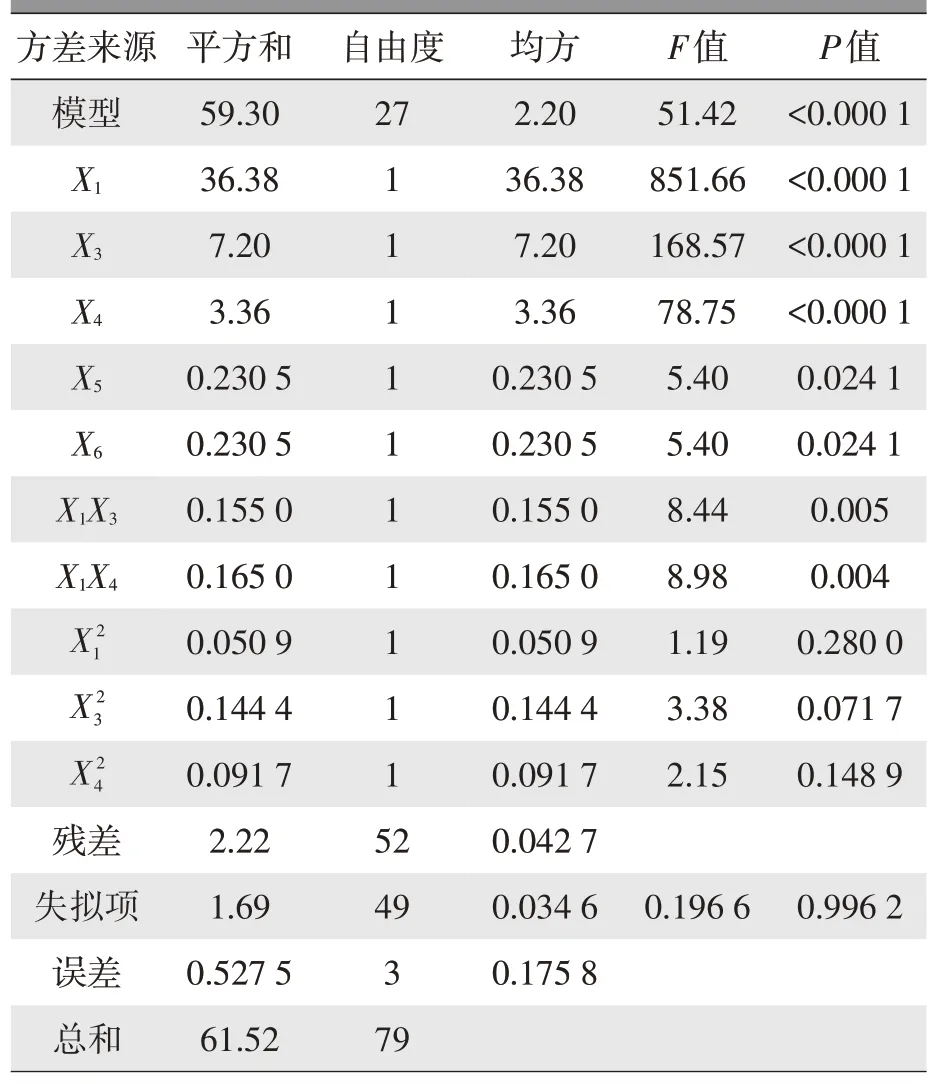
表7 基于RSM响应变量Y2回归方差分析

对试验结果进行残差分析，如图3 所示。图3a和图3d中数据点分布均匀且呈线性分布，表明数据残差符合正态分布；图3b和图3e中残差值围绕零随机分布，无任何趋势，说明拟合效果好，无异常值；图3c和图3f中实际值与预测值的点基本分布在拟合直线上，表明两者拟合程度较高。残差分析进一步证明了Y1与Y2响应曲面模型的可靠性与精确性。

图3 响应变量Y1与Y2残差分析

在各个影响因素中，取影响响应变量显著性程度最高的3 个影响因素中的任意2 个影响因素作为X轴和Y轴，响应变量的测量值作为Z轴，创建2 因素交互作用对响应变量影响的三维响应面图，如图4 所示。在响应曲面图中，曲面的倾斜度可以确定两者对响应值的影响程度，倾斜度越高，即坡度越陡，说明两者交互作用越显著。综合比较图3a～图3f，再结合表6 和表7，各因素之间交互作用对Y1、Y2的影响程度由大到小为：X4X6、X2X4、X2X6，X1X4、X1X3、X3X4。综上所述，B 柱饰板位置度（X4）与车门窗框预弯量（X6）之间的交互作用对Y1影响最显著，水切开档变化量（X1）与B 柱饰板位置度（X4）之间的交互作用对Y2影响最显著。

图4 两因素交互作用对响应变量Y1和Y2影响的三维响应曲面图

2.3 蒙特卡洛（Monte Carlo）公差分析与优化

2.3.1 理论分析

在上述响应曲面分析中，建立关于响应变量Y1、Y2的二次回归模型，即图1 中所述6σ设计公式，并分析了响应变量的显著影响因子，为后续优化分配公差奠定了基础。

蒙特卡洛模拟法是一种非线性统计学公差分析方法，实质上是随机化服从某种分布的变量并代入数学模型中来模拟随机现象，并且其模拟的准确性与模拟次数具有强关联性，本研究使用的蒙特卡洛分析软件为Minitab Workspace[8-9]。

表8 展示了各个影响因素所代表的模块及其零件装配关系，并给出了各个模块的初始总公差及标准差，其中标准差按3σ能力输入。通过蒙特卡洛分析软件模拟十万次后的结果如图5a 和图5b 所示。结果表明，Y1均值为0.529 3 mm，标准差为0.172 5 mm，且有0.62%的概率超出产品规格上限；Y2均值为3.041 4 N·m，标准差为0.215 1 N·m，有1.71%的概率低于产品下限。

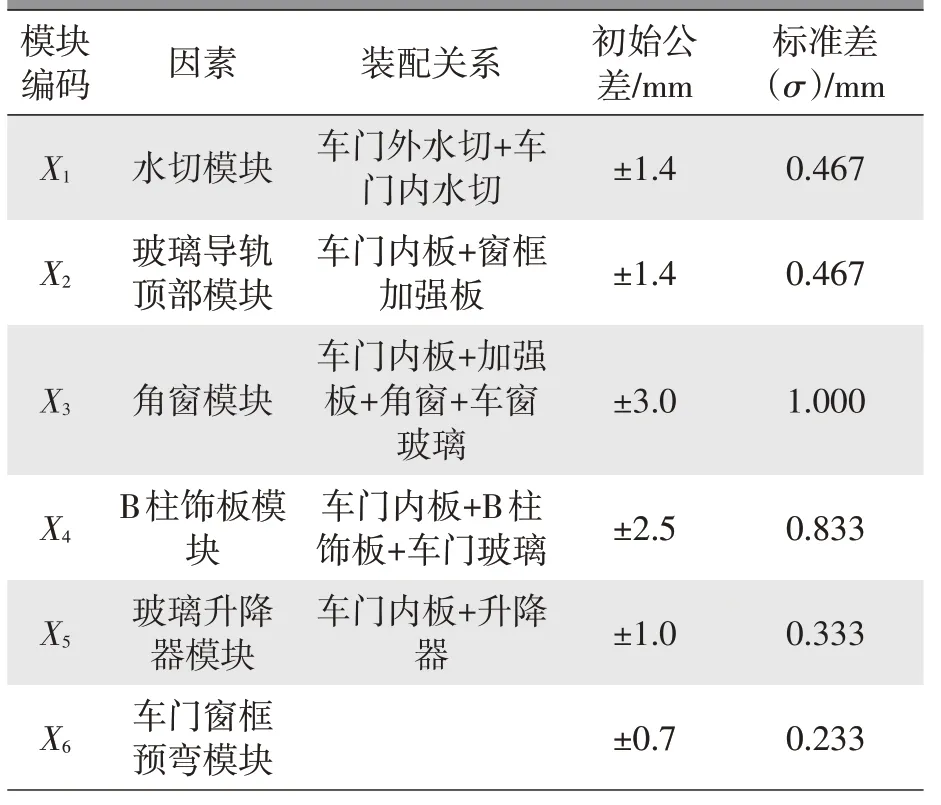
表8 模块中零件装配关系及公差

图5 基于初始公差和公差优化后蒙特卡洛模拟10万次后的结果

因此，零件的初始公差定义无法满足6σ公差设计要求，需要对零件的公差进行优化并再分配。通过对响应变量的方差分析可知，影响Y1的显著影响因素有：玻璃导轨顶部位置度、B 柱饰板位置度、车门窗框预弯量；影响Y2的显著影响因素有：水切开档变化量、角窗位置度、B 柱饰板位置度，如表6 和表7 所示。在各个模块初始公差的基础上，将水切模块、玻璃导轨顶部模块的公差带缩减为原来的1/2，B 柱饰板模块的公差带缩减为原来的1/4，之后再将其带入蒙特卡洛分析软件中，模拟10 万次后的结果如图5c 和图5d 所示。结果表明，Y1、Y2中模拟后的超差率均为0，说明在复杂系统中控制显著影响因子的公差范围有助于提升系统的稳健性。

2.3.2 实际应用

通过以上理论分析可知，缩减响应变量Y1、Y2的显著影响因子公差带，可以有效降低产品超差率，提升系统的稳健性。但受限于公差带的定义和制造能力、工艺水平、制造精度，实际生产中难以将公差带缩减到理论计算值。

对各模块及其零件的制造能力分析后，在满足零件制造能力的基础上将水切模块、玻璃导轨顶部、角窗和B 柱饰板模块公差带分别调整为±1 mm、±1 mm、±2 mm 和±1.5 mm。图6 为基于实际制造能力的公差蒙特卡洛模拟10 万次后的结果，结果表明，Y1、Y2模拟后的超差率分别为0.02%与0.04%，相比于公差优化前分别降低了0.60%与1.67%。

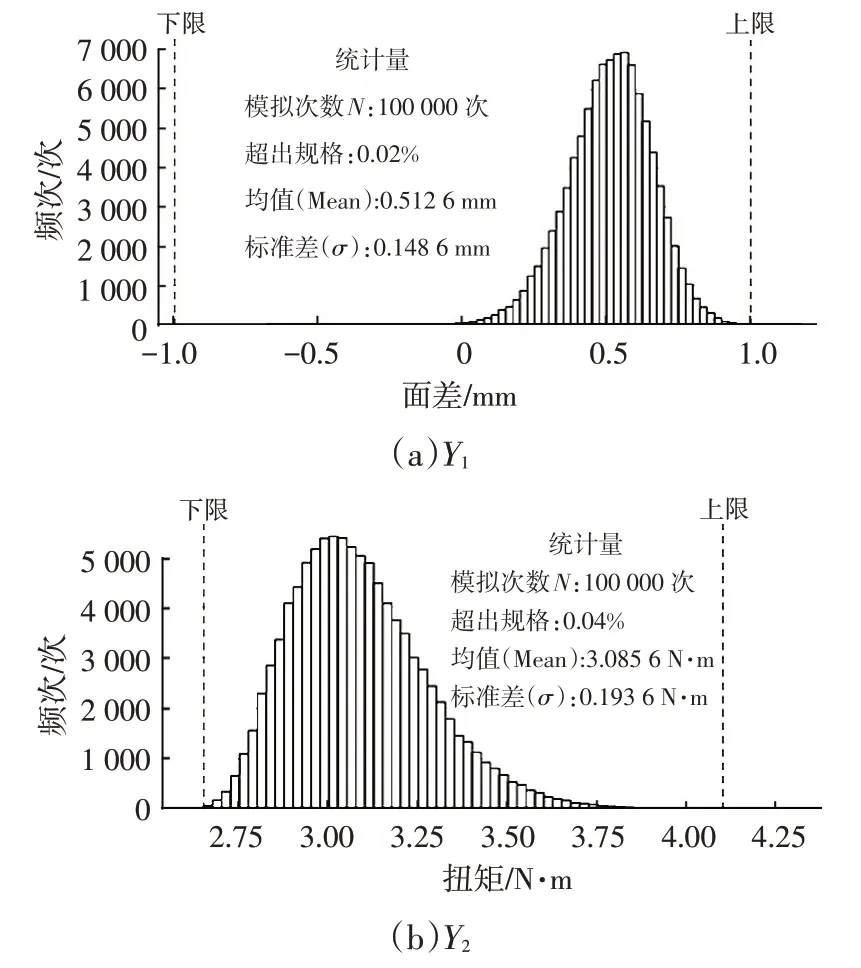
图6 基于实际制造能力公差优化后的蒙特卡洛模拟10万次后的结果

3 结论

a. 以玻璃面差和扭矩为响应变量，水切开档变化量、玻璃导轨顶部位置度、角窗位置度、B 柱饰板位置度、玻璃升降器位置度和车门窗框预弯量为考察因素，利用响应曲面试验设计建立了关于响应变量的二次回归模型。经方差分析验证，2 个回归模型均具有较好的拟合效果和可靠性。

b. 基于响应曲面方差分析可知，Y1的显著影响因素有玻璃导轨顶部位置度、B 柱饰板位置度、车门窗框预弯量；Y2的显著影响因素有：水切开档变化量、角窗位置度、B 柱饰板位置度。

c. 根据响应曲面试验建立的二次回归模型，优化了响应变量Y1、Y2显著影响因素的公差，蒙特卡洛分析表明，理想化公差的响应值超出规格限的概率为0，基于零件实际制造能力的公差其超出规格限的概率分别为0.02%与0.04%，相比于公差优化前分别降低了0.60%与1.67%，大幅度提升了系统的稳健性。