悬架局部屈曲损伤估算及疲劳目标修正

黄东海 赵振奇 王聪聪 吴维冬

（东风汽车有限公司东风日产乘用车公司技术中心，广州 510800）

1 前言

由宽而薄的板材制成的结构件容易发生局部屈曲，屈曲发生后可能发生内力重分布，由刚性更高的区域承受载荷[1]，不会立即发生功能失效。但局部屈曲对于零件的整体强度和耐久不利。国内外也有较多相关研究报道，石永久等[2]对局部屈曲退化行为的钢材本构模型进行了研究，并探讨了影响构件局部屈曲损伤退化的因素，提出了不同控制因素下损伤退化规律。在汽车设计领域，随着国家能耗要求不断提高，汽车轻量化愈发紧迫，高强度钢材能较好的兼顾轻量化和成本。车身和底盘结构件都逐步导入高强度板材，板材强度提高，厚度则相应减小，在截面轮廓不变时，提高了零件局部屈曲风险。

在某车型开发中，底盘副车架在强度试验中发生局部屈曲，局部屈曲后仍能承受更大载荷（分支点失稳）。同时，局部屈曲部位与应力集中点相近，且早期设定的可靠性目标是以不发生局部屈曲为前提的正弦波单级谱定数截尾耐久试验目标，因此需要评估局部屈曲对剩余强度的影响，进而修正耐久目标。

2 某车型底盘零件局部屈曲

2.1 局部屈曲发现及CAE风险确认

在X 车型开发中，在底盘台架强度试验中发现副前车架下板部位A 附近传感器存在异常信号，查看录像发现疑似出现局部屈曲。因为数据阶段并未识别出该部位局部屈曲的风险，所以仅通过计算机辅助工程（Computer-Aided Engineering，CAE）获取了应力分布，并未实施局部屈曲的CAE 风险评估。如图1 所示，部位A 板材主要受平面应力或单向应力作用，主应力方向未知，根据CAE 模拟的范式等效应力值（Von Mises Stress）为265 MPa。部位B 存在应力集中，在耐久试验中出现了开裂现象，如图2 所示，一定程度上验证了该应力分布的准确性。A 点和B 点距离为55.4 mm，部位B 耐久性能存在局部屈曲后恶化的风险。

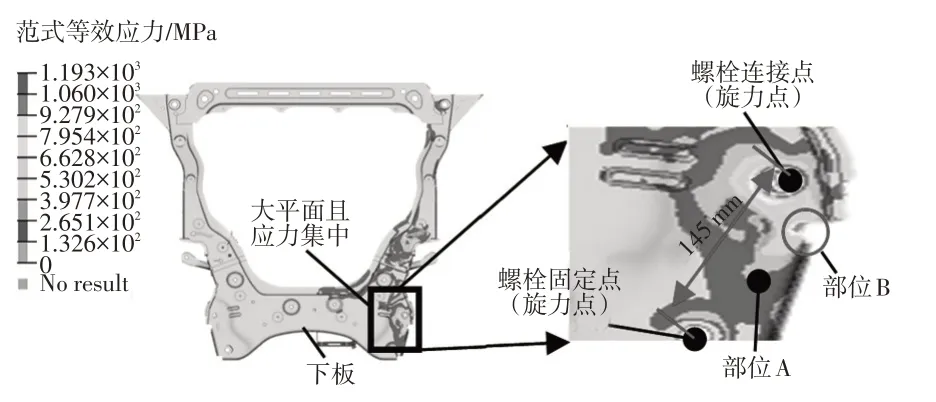
图1 前后方向强度载荷作用下应力分布

图2 前后方向耐久试验裂纹

为缩减解析时间，通过欧拉公式计算临界屈曲应力，并与部位A 应力比较，从而确认屈服风险。

由图1 可知，部位A 位于2 个螺栓连接点中间，是一块较平整的薄板，尺寸参数如图1 所示，根据欧拉临界屈曲应力公式计算屈曲的临界应力值σcr如下[3]：

式中，E为材料的弹性模量，本案例中取值为210 000 MPa；ν为材料泊松比，取值为0.26；L为板材的受力两端距离，本案例中取值为145 mm；t为材料厚度，本案例中取值为2.0 mm。

计算得其局部屈曲临界应力值为106 MPa，小于CAE 最大主应力265 MPa，说明部位A 存在发生局部屈曲的风险。

2.2 局部屈曲确认

为确认局部屈曲的临界点，在部位A 处布置位移传感器检测板材法向的变形量。试验台架如图3 所示，模拟实车工况，搭建悬架总成强度试验台架，在轮胎接地点施加前到后载荷，图中所用位移传感器量程为30 mm，分度值为0.01 mm。

图3 局部屈曲临界载荷测量台架

采用步进式静态加载，步长为1 kN，位移传感器数据如图4 所示。部位A 处位移信号检测到分支点屈曲现象。局部屈曲的临界载荷为9 kN。

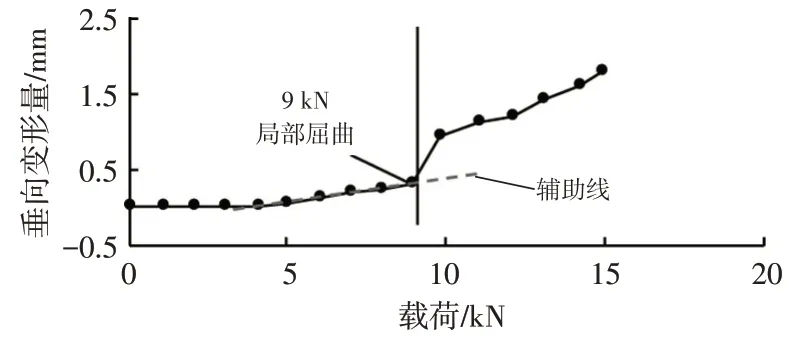
图4 局部屈曲测量

3 局部屈曲后疲劳寿命预估模型

汽车开发过程中常用计算机有限元仿真预估零件的损伤和寿命[4-5]，国内学者对于冲击载荷下疲劳寿命也进行过相关研究，王显会等[6]采用有限元法对特种车辆冲击载荷下的疲劳寿命进行了预估。对于冲击载荷下局部屈曲对疲劳寿命的影响可能属于低周疲劳的范畴。本应使用应变-寿命曲线（ε-N曲线）或全域疲劳加载下的剩余强度退化模型[7]进行预估，但本课题对象部品基于应力-寿命曲线（S-N曲线）开发，没有获得材料的ε-N曲线，剩余强度退化参数也不明，因此，采用彭兆春提出2 种模型[8]：一是综合考虑了载荷顺序效应以及前后级载荷间交互作用的疲劳损伤累积模型；二是基于动态剩余S-N曲线与材料记忆退化的线性损伤累积模型，分别结合S-N曲线对局部屈曲后疲劳寿命进行预估，并对预测结果进行对比。

模型1：如图5 所示，对称应力σ1加载Nf1次后疲劳失效（OAE），对称应力σ2加载Nf2次后疲劳失效（OBE），σ1加载n1次后，只考虑载荷顺序效应时，等效于σ2加载次，损伤D沿OABE 积累；在考虑前后级载荷间交互作用时，等效于σ2加载次，损伤D沿OABCE 积累，继续用σ2加载n2次后疲劳失效。

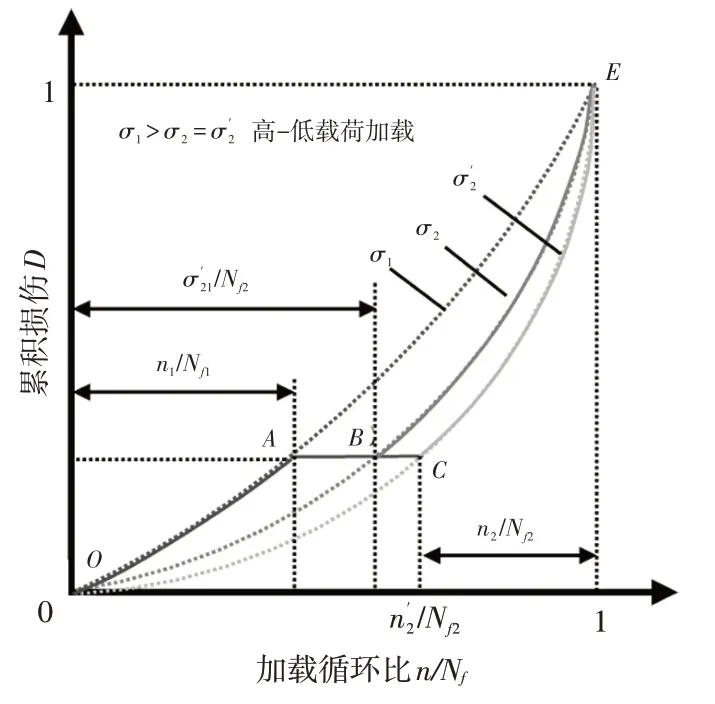
图5 模型1示意

损伤等效公式如下：

模型2：如图6 所示，σ1加载n1次后，不考虑载荷顺序效应时，S-N曲线退化为剩余S-N曲线，考虑载荷顺序效应时，S-N曲线退化为动态剩余S-N曲线，改为σ2加载n2次后疲劳失效。

图6 模型2示意

损伤等效公式如下：

4 局部屈曲损伤预估与试验对比

4.1 应力测量

该失效部位材料为低碳钢，性能等同于JIS 牌号为SPFH590 的热轧板，其成分如表1 所示。

表1 类SPFH590成分表（质量分数）%

更换新样件，在裂纹起始点旁边黏贴应变片，测量载荷-应变曲线，如图7 所示。

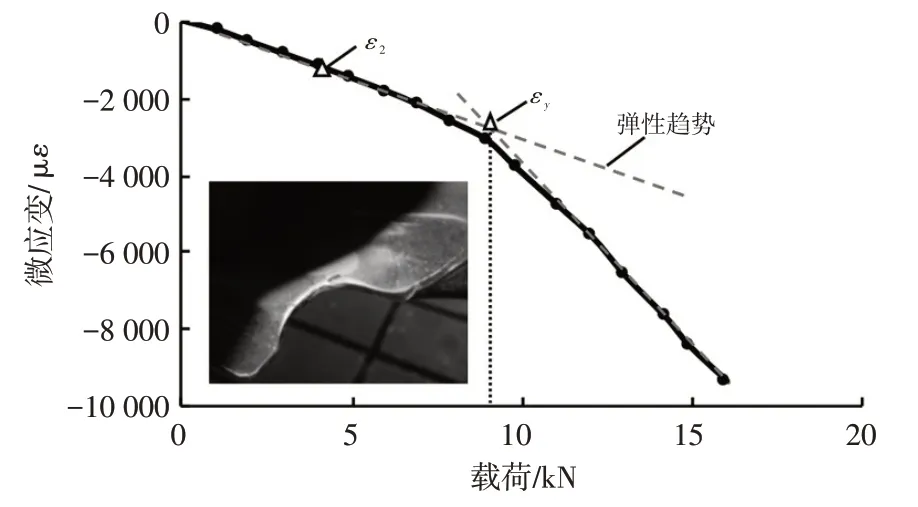
图7 应力测量

耐久载荷为（0±4.07）kN，其应变实测值ε2在弹性范围，可用于计算应力值，计算结果如表2所示，弹性模量E取值为2.1 GPa；强度载荷为0~15 kN，由于在9 kN 时（εy处）发生了局部屈曲，根据实测应变曲线，计算得15 kN 时塑性应变为εp，其应力采用统一材料法则估算[9]为-520 MPa，小于材料屈服强度588.6 MPa。实测载荷-应变曲线变曲点处（εy处）应力为-570 MPa，与材料屈服强度相近。另外，局部屈曲后板材一面受压应力，另一面受拉应力，拉应力侧损伤更大，取拉应力侧为研究对象，假设拉应力与压应力绝对值相等，其应力计算结果如表2 所示。

表2 载荷-应力列表

采用Goodman方法对0~15 kN加载的应力进行平均应力修正。材料的抗拉强度σu=623 MPa。修正后的载荷和应力如表3 所示。其中，σ11和σ12为强度载荷0~15 kN 作用下，分别用εp和εy计算得到，并用Goodman 方法修正后的等效应力幅值。

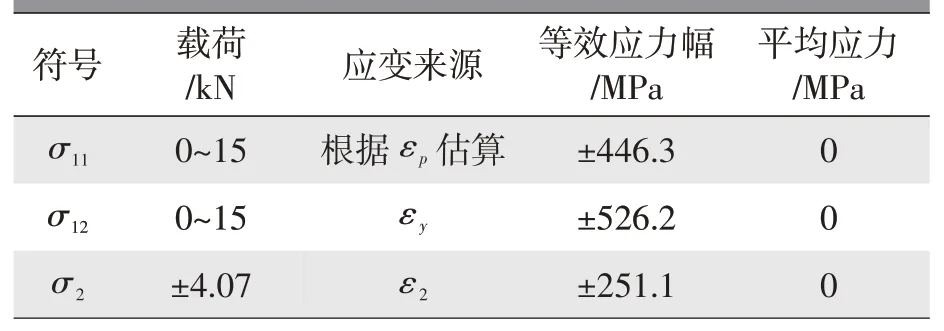
表3 载荷-等效应力列表

4.2 S-N曲线修正

S-N曲线如图8 所示，考虑该部位有明显的圆角缺口，故采用文献[9]的海伍德模型进行修正，如图9 所示。

图8 板材S-N曲线

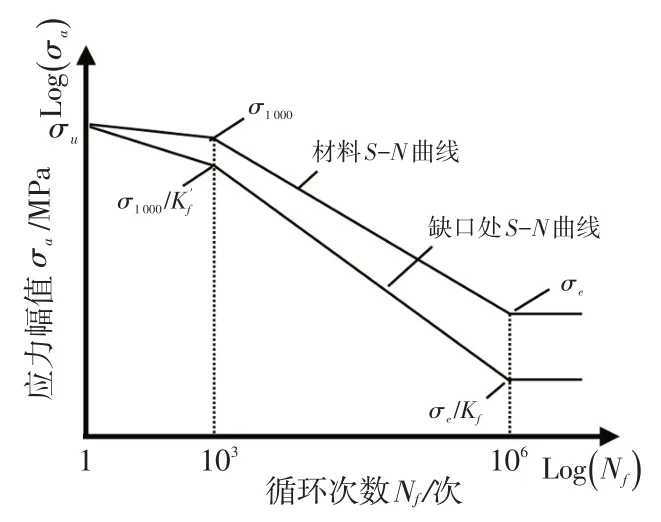
图9 切口效应模型

缺口处疲劳极限按如下公式修正：

式中，σe为原S-N曲线疲劳极限；Kf为疲劳强度折减系数。

Kf计算如下：

式中，Kt为应力集中系数，可由CAE 模拟获得，本案例中Kt取值为1.99；q为灵敏度系数。

q计算如下：

式中，r为缺口根部半径；a为与晶粒尺寸和加载方式相关的材料常数。

对于拉伸载荷，a的经验公式如下：

式中，σu为抗拉强度。

缺口处S-N曲线，寿命为1 000 次对应的应力幅值按下式修正：

式中，σ1000为原S-N曲线寿命为1 000 次对应的应力幅值；为在1 000 次循环时的疲劳强度折减系数。

按下式计算：

图10 应变片处S-N曲线

4.3 寿命预估与试验验证

根据应变片处S-N曲线，计算σ11、σ12对应的寿命，如表4 所示。将表4 数据分别代入式（2）和式（3）可以估算σ1加载12 次后（已发生局部屈曲）按σ2加载的剩余寿命n2，计算结果如表5 和图11所示。

表4 应力-寿命列表

表5 剩余寿命n2验证

图11 预估偏差

可见，式（2）和σ12的预估偏差均值较小，所以在本例中选取式（2）和σ12组合对局部屈曲损伤进行估算更合理，其估算结果小于实测值，相对更安全。但需要指出的是σ12是实测的固定值。当σ1对应的载荷超过屈服点不多的情况下，估算结果偏严格。而此时应优先采用σ11结合式（2）进行预估，因为σ11是根据实测的塑性应变计算而得的变量，但其具体择用标准尚不明确。

5 单级谱耐久目标修正

根据实际需求，确定强度载荷幅值和n1，测量并计算σ12和σ2，结合实测的Nf2，代入式（2）算得n2，然后按公式（10）对Weibull 分布F(t)=50%的原耐久目标值进行修正。

虽然可以对局部屈曲的损伤进行评估，但是车辆使用中大于局部屈曲载荷的发生次数和幅值往往难以准确预估，所以通常难以准确修正其目标，工程中最实际的做法是避免应力集中点附近出现局部屈曲现象。

6 结束语

本文针对车型开发中发现的局部屈曲现象，通过应力测量，修正S-N曲线，结合基于考虑了载荷顺序以及交互作用的疲劳损伤累积模型和动态剩余S-N曲线2 种方法，预估了零件的残余寿命，并与试验实测残余寿命进行比较，进而提出了耐久目标修正方法，得出以下结论：

a. 考虑了载荷顺序以及交互作用的疲劳损伤累积模型对局部屈曲后残余寿命的预估相对更准确。

b. 实测屈服强度σ12对局部屈曲后残余寿命的预估相对严厉，较安全，缺点是该预估值不会随强度载荷大小变化而变化。基于统一材料法则，结合实测塑性应变估算的σ11则对局部屈曲损伤预估准确性低，但其预估值随强度载荷变化。

c. 提出了考虑局部屈曲的耐久目标修正方法，同时应避免应力集中点处发生局部屈曲。